Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

неизвестное 6х с номером / равно числу /-й элиминационной строки

из столбца I плюс сумма произведений уже вычисленных неизвест-

ных 6х на расположенные над ними числа из этой же элиминационной

строки.

Приводим также полную так называемую «школьную» схему Гаус-

са (схема 4) лишь с целью разъяснения порядка вычислений при рас-

крытии алгоритмов Гаусса. Однако следует отметить, что необхо-

димость выполнения записей промежуточных вычислений может

внести только дополнительные ошибки и увеличить время вычислений.

Поэтому сразу необходимо приучить себя к применению метода накоп-

ления, т. е. пользоваться сокращенной схемой.

В прил. XIII.10 и XIII.11 приводятся программы для кальку-

лятора «Электроника БЗ-21» вычисления выражений вида [х

], [ху]

и перемножения строки с на матрицу А, что обеспечивает автомати-

зацию составления и решения нормальных уравнений и вычисления

поправок.

Контроль вычисления неизвестных Ьх

)

можно осуществить путем

подстановки их в /-е эквивалентные уравнения (3.25). Для того чтобы

судить о влиянии ошибок округления, неизвестные следует подставить

в исходную систему нормальных уравнений (это целесообразно делать

при большом числе неизвестных). Если отклонения от нуля в правых

частях окажутся существенными, то следует неизвестные уточнить,

решая систему со свободными членами, равными е^.

Существует также иной надежный способ текущего контроля вы-

числения всех неизвестных Ь

Х]

, начиная с последнего. Напишем вы-

ражения (3.29) в матричной форме

Ае + Ь = 5, (3.35)

где векторы

называются соответственно суммирующим и суммарным. Умножая

(3.35) слева на матрицу А

, получим систему нормальных уравнений

Не + ЛЧ, = А

8 (3.36)

относительно неизвестных в] = 1. Из сравнения системы (3.36) с сис-

темой нормальных уравнений (3.19), для которых справедливы экви-

валентные уравнения (3.25), так как обе системы нормальных урав-

нений имеют одну и ту же матрицу К, сразу следуют контрольные

равенства (3.30'). Далее, вычитая из (3.19) систему (3.36), находим

НАх + Л

5=0, (3.37)

где вектор

Ах = Ах —е. (3.38)

154.

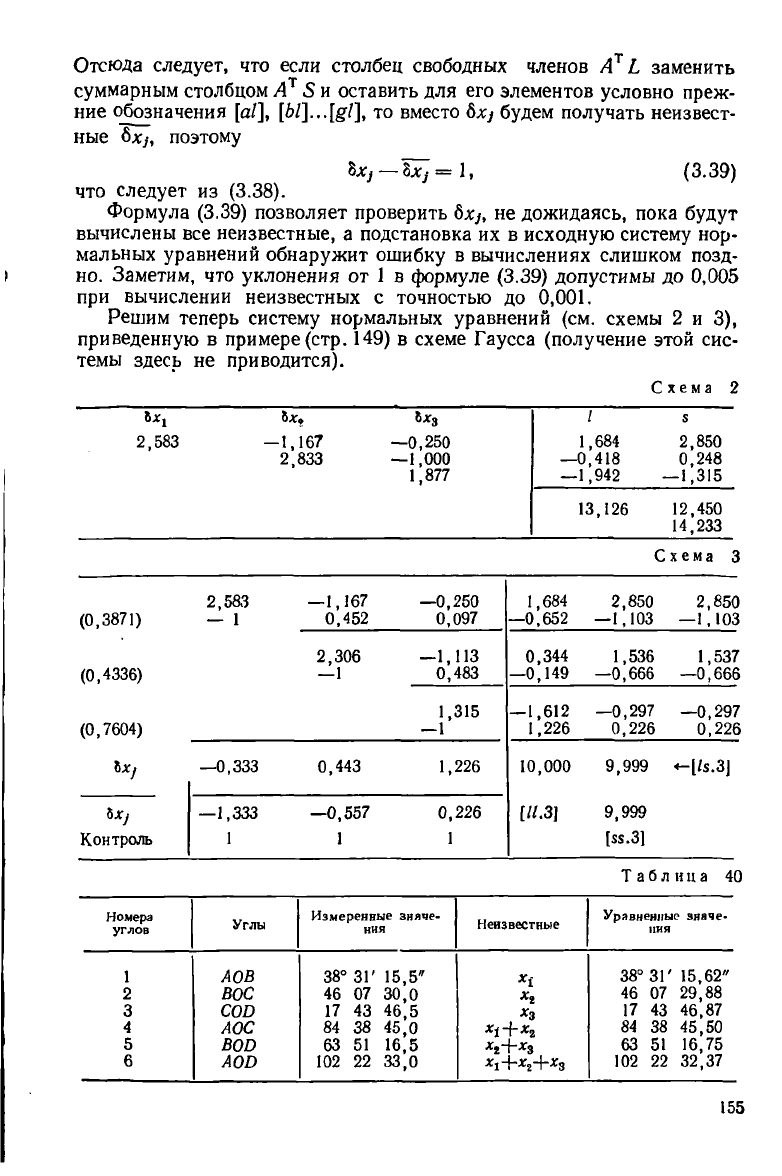
Отсюда следует, что если столбец свободных членов А

Ь заменить

суммарным столбцом А

8 и оставить для его элементов условно преж-

ние обозначения [а/], то вместо Ьх] будем получать неизвест-

ные Ьх], поэтому

Ъх

}

— Ъ^=1, (3.39)

что следует из (3.38).

Формула (3.39) позволяет проверить Ьх], не дожидаясь, пока будут

вычислены все неизвестные, а подстановка их в исходную систему нор-

мальных уравнений обнаружит ошибку в вычислениях слишком позд-

но. Заметим, что уклонения от 1 в формуле (3.39) допустимы до 0,005

при вычислении неизвестных с точностью до 0,001.

Решим теперь систему нормальных уравнений (см. схемы 2 и 3),

приведенную в примере (стр. 149) в схеме Гаусса (получение этой сис-

темы здесь не приводится).

Схема 2

5лг»

&дг

2,583

-1,167

2,833

—0,250

—1,000

1,877

1,684

-0,418

1,942

2,850

0,248

—1,315

13,126

12,450

14,233

Схема 3

(0,3871)

2,583

— 1

—1,167

0,452

—0,250

0,097

1,684

—0,652

2,850

—1,103

2,850

—1,103

(0,4336)

2,306

—1

—1,113

0,483

0,344

—0,149

1,536

—0,666

1,537

—0,666

(0,7604)

1,315

—1

—1,612

1,226

—0,297

0,226

—0,297

0,226

Ьх,

—0,333 0,443 1,226 10,000

9,999

« [/5.3]

Х]

—1,333

—0,557

0,226

[«.3]

9,999

Контроль

1 1 1

[55.31

Таблица 40

Номера

углов

Углы

Измеренные значе-

ния

Неизвестные

Уравненные значе-

ния

АОВ

ВОС

СОО

А ОС

ВОй

АОй

38° 31'

46 07

102

15,5"

30,0

46,5

45,0

16,5

33.0

х.

+х

38°

102

31' 15,62"

07 29,88

43 46,87

38 45,50

51 16,75

22 32,37

155.

3.17. В табл. 40 даны результаты измерения уг-

лов во всех комбинациях (рис. 45). Уравнять эти ре-

зультаты параметрическим способом.

Решение. 1) Выберем в качестве независимых

неизвестных (параметров) Х

1р

, Х

соответственно

первый, второй, третий углы. Тогда остальные три

угла, зависящие от первых трех, будут представлять

собою суммы независимых неизвестных. Уравнения

связи имеют вид

У* = Х

; К

= Х

+ X,;

= Х

; К

= X., Х

;

= ^в = + Х

+ ^з-

2) Записываем уравнение поправок в общем виде

РИС. 45

5*, + 1

= «х

, 5*1 + 5*2 + '4 = 04;

+ /

= о

; 5*

+ 5*3 + /

= VI-,

хз + 1э = °э'> 5*

+5*

+ 8*

+ /

= 1>

(3.40)

3) Введем приближенные значения неизвестных, приняв их равными изме-

ренным значениям углов х

, *

„(0)

38°3 Г15,5"; 4

= 46°07'30,0"; = 17°43'46,5".

4) На основании (3.4)] вычислим свободные члены как разности прибли-

женных значений углов и' измеренных. Получаем

и = 0; /

= -Ь 0,5";

о;

= 0;

= 0; /, = -1.0*

5) По уравнениям (3.40) составим таблицу коэффициентов уравнений попра-

вок и нормальных уравнений (табл. 41, 42).

Таблица 41

Номера

Коэффициенты

измерений

•

0,12"

1 —0,12

0,37

1 1

0,5

2,5 0,50

5 1 1

0,5

2,0

0,25

— 1,0

2,0

—0,63

3 4

3 —0,5

9,5 [от]=0,86

0,124

—0,122 0,373 [/о]=0,88

И=0,874

[от]=0,86

\со]

[/о]=0,88

И=0,874

—0,01

6) Затем решим нормальные уравнения (табл. 43).

Как видим, все предусмотренные контроли выполняются. Уравненные

значения углов приведены в табл. 40 в последнем столбце.

Окончательным контролем решения задачи является выполнение равенств

УI

фI» *з). в чем легко убедиться непосредственной проверкой.

156.

Таблица 54'

Ь]

с]

Контроль

3,00

2,00

4,00

1,00

2,00

3,00

—0,50

-0,50

— 1,00

5,50

7,50

5,00

5,50

7,50

5,00

3,00

1,25

—0,75

17,25

—0,75

17,25

Таблица 43

Вспомогательные

величины

г*,

$ Контроль

(0,3333)

3,00

(-1)

2,00

—2,667

1,00

—0,333

—0,50

0,167

5,50

— 1,833

5,50

—1,833

(0,3745)

3,00

(-1)

2,67

(-1)

1,33

(—0,498)

—0,17

0,064

3,83

—1,434

3,83

— 1,434

(0,5000)

2,00

(-0

—0,75

0,373

1,26

—0,627

1,25

—0,627

0,124

—0,875

—0,122

0,878

0,373

—0,621

0,88

0,89

0,999

1,000

§ 30. ОЦЕНКА ТОЧНОСТИ УРАВНЕННЫХ НЕИЗВЕСТНЫХ

В методе наименьших квадратов доказывается, что обратные веса>

уравненных неизвестных

1 /Дг,=<2я. (3.41)

где 0.1] — так называемые весовые коэффициенты. Они являются диа-

гональными элементами матрицы

^11 <2X2 • •

(2 = 1 Си • • 1. (3.42)

получаемой обращением матрицы Я, т. е. ^ = Я'

. Так как Я0 = Е

то, обозначив /-й столбец матрицы 0 через 0ь

матрицы Е — через

Е], получим к систем нормальных уравнений вида

Щ = Е,. (3.43)

157

Как видно, системы (3.43) и (3.19) имеют одну и ту же матрицу ко-

эффициентов Отсюда следует, что для вычисления элементов столб-

цов 01] матрицы ф в схему Гаусса необходимо дополнительно ввести

столбцы — Е), равные

и, рассматривая их как новые столбцы свободных членов, по каждому

из них получить к столбцов <2;. Более того, если каждый из столб-

цов — Е] условно обозначить как столбец свободных членов

то элементы столбцов получим по тем же формулам, что и

неизвестные Ьх

}

Так, в задаче 3.17 вычисление величин приведем в табл. 44.

Контролем вычислений являются равенства (}

{]

= С1

!и

так как

матрица <2, как и Я, симметричная. Обычно при вычислениях табл. 43

и 44 совмещают, помещая столбцы —Е

}

вслед за столбцом «контроль»

в табл. 43, а элементы

С}

и, ниже строки «контроль» в левой нижней

части этой таблицы.

Таблица 44

5*.

8*,

-Е,

-В,

—Е,

3,00

—1,00

2,00

—0,667

1,00

—0,333

—1

0,333

2,67

—1,000

1,33

—0,498

0,67

—0,251

—1,00

0,374

458.

2,00

-1,000

— 0,250 0

+ 0,499 —0,250

— 0,250 +0,500

0,50

—0,250

—1,00

0.500

^и 0и <3хз

= I $21 <2*2 <2*3

^31 Ззз

Приведем дополнительно способ вычисления любого элемента

матрицы <3, не требующего знания остальных ее элементов. Он основан

на следующих соображениях.

Матрицу коэффициентов нормальных уравнений всегда можно

представить в виде произведения двух треугольных матриц Т

{

и Т

/[аЬ] \ р

аа

\ Ш • • -[

ЯГ

[аа] | _ I

[66.1]

. .

.[Ье-1]

составленных из элементов элиминационных строк, взятых с обрат-

ным знаком, и эквивалентных строк схемы Гаусса. Собственно на этом

представлении и основан способ Гаусса. Так как ^<2 = Е, то полу-

чаем Г,Г

<2 = Е, откуда следует <2 = /Г

= Т~\Т~\.

Можно показать, что элементы матриц Т~\ и Т~\ как раз и со-

держатся в столбцах ЕI таблиц: в нечетных строках с обратным зна-

ком элементы матрицы Т~\, а в четных — элементы матрицы (Г

^)*-

Так, в нашем примере

'0,333 —0,251 0

Т~

= I 0,374 —0,249

0,500

Т~

= ( —0,67 1 0

0 —0,50 1

Перемножив эти матрицы, получим матрицу (?. Но вычисления

удобно выполнять в таблице вида табл. 44 по следующему правилу;

любой элемент матрицы ф равен взятой с обратным знаком сумме

произведений чисел всех элиминационных строк из столбца —Е

на

элементы эквивалентных строк из столбца —Е

}

(так называемый спо-

соб диагоналей). Например, <2

= —(0,333 — 0,67 х 0,251) = 0,500„

<2*2 = —(0,374 - 0,250 X 0,50) = 0,500, = —0,251 и т. д.

Средние квадратические ошибки уравненных неизвестных вычис-

ляют по формуле т

Х]

= где для равноточных измерений

средняя квадратическая ошибка одного измерения вычисляется по-

формуле т

Х]

= У [у

]/(п—к) (обобщение формулы Бесселя, полу-

чаемой при к = 1). Так, в задаче 3.17 т = /(ЩГ/(6—3) = 0,54" и

Х1

= т

Х2

= т

Хз

= 0,54

]/"О7БО"

= 0,38",

матрицу М

= т

<? называют корреляционной матрицей уравненных

неизвестных (см. § 22).

159.

Заметим, что г

аи

есть коэффициенты корреляции

между уравненными 1-й и /-м неизвестными. Так, коэффициент корре-

ляции между первым и вторым углом

- _1°-

250

=-0,5.

Ко.500 V 0,500

Способ Ганзена вычисления весовых коэффициентов. Рассмотрен-

ный выше способ вычисления весовых коэффициентов называют спо-

собом дополнительных столбцов. В этом способе вычисляют все ве-

личины . Однако объем вычислений можно сократить, если вос-

пользоваться свойством симметричности матрицы С. В самом деле,

приняв для простоты к = 3, напишем три системы эквивалентных

уравнений, соответствующих системе нормальных уравнений (3.43).

Будем иметь

[аа] Яи + \аЬ\ + \ас\<2

- 1 = 0;

[ЬЪЛ\ (2

+ \ЪсЛ\ Ф

+ ? = 0;

[сс.2|<г

+ ? = 0;

|аа\ (}„ + \аЬ\ (?

+ \ас\

= 0;

[Ш]<г

+ [йс.1]0» —1 =0;

[сс.2] д

з2

+ ? = 0;

\аа]

+ \аЬ]

+ [ас]

= 0;

1Ш1д

+ 16с.1]<г

= 0;

1=0.

(3.44)

(3.45)

(3.46)

|сс.2]Сзз.

Здесь знаком вопроса заменены свободные члены этих уравнений, вы-

числить которые не придется. Далее из последнего уравнения системы

(3.46) сразу находим

Ззз = ТТ^ • (3-

6')

из второго уравнения

«3

и, наконец,

[сс. 2]

_ [6с. 1]

[66.1]

<33

О _ [

аЬ

\ п о

^13 ~~ ТТТГ^з 7777 ^ззч

[ас]

[ааГ

[аа]

Таким образом, для вычисления столбца

'<?13

160

вводить дополнительный столбец свободных членов и не требуется

(величина — уже содержится в схеме Гаусса как вспомогательная

[сс.2]

величина, остальные же числа элиминационных строк этого столбца

равны нулю).

Поскольку <2зг = Фгз. то последнее уравнение в системе (3.45) для

определения С

не потребуется. Приняв в качестве <3

Э2

величину (2

из второго уравнения (3.45) находим

О !

422 —

Ь(, ,

... ,, "<32»

[66.1] [66.1]

а из первого уравнения

О —

Д&

[аа]

[дс!

[аа]

Замечаем, что величина ^ ^ уже имеется в схеме Гаусса, а эле-

мент первой элиминационной строки в дополнительном столбце сво-

бодных членов равен нулю. Так что и для получения столбца как

и столбца «2з, также не нужно вводить дополнительный столбец. Рас-

суждая аналогичным образом и переходя к системе (3.44), находим

Он = +

И) О

[аа] [аа]

[ас]

[аа]

С13>

приняв = С?

, <2,

= <2

Ясно, что и в этом случае нет необходимости вводить дополни-

тельный столбец свободных членов.

Вычисления целесообразно располагать по следующей схеме (на

примере задачи 3.17).

(0,3333)

3,00

(-1,000)

2,00

—0,667

1,00

—0,333

(0,3745)

2,67

(—1,000)

1,33

—0,498

(0,5000)

Контроль

2,00

(—1,000)

1,000

0,500

—0,250

0,998

—0,250 0,499

—0,249

1,002

—0,249 0,500

= 0

6 4-258

161.

В ней вычисления начинают с последней строки (в которой разме-

щают элементы столбца <2

), как описано выше. В дальнейшем все

вычисляемые величины заносят в нижнюю часть этой схемы, выде-

ленную жирной ломаной линией. В верхнюю же часть заносят числа

из нижней по мере продвижения по строкам вверх. Так, вычислив

элементы третьей строки, число —0,249 переносят во вторую строку, а

вычислив элементы второй строки, начиная с 0,499, в первую строку

переносят элементы —0,250 из второй строки и из третьей. В первой

строке вычислений находится лишь элемент = 0,500.

Следует, однако, иметь в виду, что при вычислении этим спо-

собом ошибки, которые могут быть допущены, не обнаруживаются

и вся матрица <2 может быть получена неверной. Поэтому каждый

столбец (}}, начиная с последнего, следует контролировать допол-

нительно. Необходимые для этого равенства вытекают непосредствен-

но из формулы (3.43) и имеют вид

\ас]С1

+ \Ьс\С1ъ + \ас\(1м = \\

{аЬ\С1ъ + \ЬЬ]С1

гг

+ \Ьс\С1

гз

= \\

+ [аЬ]

С2

+ (ас] = 1.

Полученные правые части этих равенств целесообразно записать

в специальном столбце «Контроль» (см. схему). Расхождения здесь

допустимы до 0,002—0,003 (при вычислении элементов матрицы ф —

до 0,001).

Хотя этот способ изложен нами для к = 3, его несложно обобщить

и на любое число к. Заметим также, что оба рассмотренных способа

применяют для обращения симметричных матриц как вручную, так

и на ЭВМ и называют способом Гаусса.

Из формул (3.41) и (3.46') следует сразу, что вес последнего неиз-

вестного = [сс.2] или в общем случае

Рх

= ШЛ* — 1)]. (3.46")

Нетрудно получить также формулу для вычисления веса пред-

последнего неизвестного

\ЬЬЛ]

[сс.1]

или в общем случае

[88-(к- 2)|

Их

Так, в нашем примере р

, = 2,00.

Алгоритмы Гаусса

[ЬЬ.

1 ]

= 2,67, [сс.

1 ]

= 2,00 + 0,67 = 2,67.

Поэтому

р = ^ 2,00 = 2,00.

2.67

162.

Так как веса я и р легко вычислить, то последними в геоде

зической сети обычно нумеруют те пункты, которые предполагают наи

менее точными из всех (расположенные в самом слабом месте).

3.18.

дующих систем

Решить по способу Гаусса, применяя сокращенную схему, одну

истем нормальных уравнений:

из еле

+ 10*{— 2*

— 3 =

1 2*, + 14*2- 3*3 - 7 =

- 3*2+П*з +

2) +8*,— *

\ + 12 *

2*з +

*з +

+ 2*!- *

+ 13 *

+ 15 *, + 3 *

— *

+ 3*,+ 10*2+ 2*з —

- *,+ 2*2+12*3 +

+ 16*! + 2*

- З*

+ 2

дг,

1.4

+ 4*з +

- 3*,+ 4*2 + 18*

4 =

2 = 0

5 = 0

6=0

4=0

3 =» о

6=0

4 = 0

8 = 0

— 88 = 0

, — 70 = 0

5) + 27 *, + 6 *2

+ 6*,+ 15*2+ Я

+ *2 +54*з—107 = 0

6) + 20

— 2 *

+ 3 *

— 10 = 0

— 2 *, + 24 *

- 4 *

+ 13 = 0

+ 3 *, — 4 *

+ 18 *

— 8=0

7) +16*, + 3*2- 2*з+ 9 = 0

+ 3*, + 19*2 + 4*з-12 = 0

— 2 *,- + 4 *

+ 11 =

8) +13*, — 3*2— 5*з+ 6 = 0

-3*^ + 17*2+ *

- 11 =0

7 = 0

5 = 0

8 = 0

4 = 0

- 5 + *2 +

9) +21 *, - 4*2 +

3*з-

- 4* +16*

— 2*з +

+ 3* - 2*2+12*3 +

10) + 76 *, — 30 *2 — 20 *

+2,8= б

- 30 *, + 83 *

— 25 *

—4,1= 0

—.20 *, — 25 *2 + 89 *

— 1,9= 0.

От в еты:

0,402

— 0,408

•0,557

0,356

2,468

0,413

7) —0,834

8) —0,559

9) 0,209

10) —0,013

0,509

0,107

0,648

0,318

3,552

— 0,462

0,927

0,583

— 0,506

0,050

— 0,225.

— 0,314.

— 0,404.

0,314.

1,915.

0,272.

— 0,779.

— 0,705.

— 0,470.

0,028.

3.19. Обратить по способу Ганзена матрицу коэффициентов одной из систем

нормальных уравнений, приведенных в задаче 3.18.

3.20. Является ли нормальной матрица

Указание) Вычислить ее определитель согласно формуле (3.28).

Ответ: нет.

163