Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

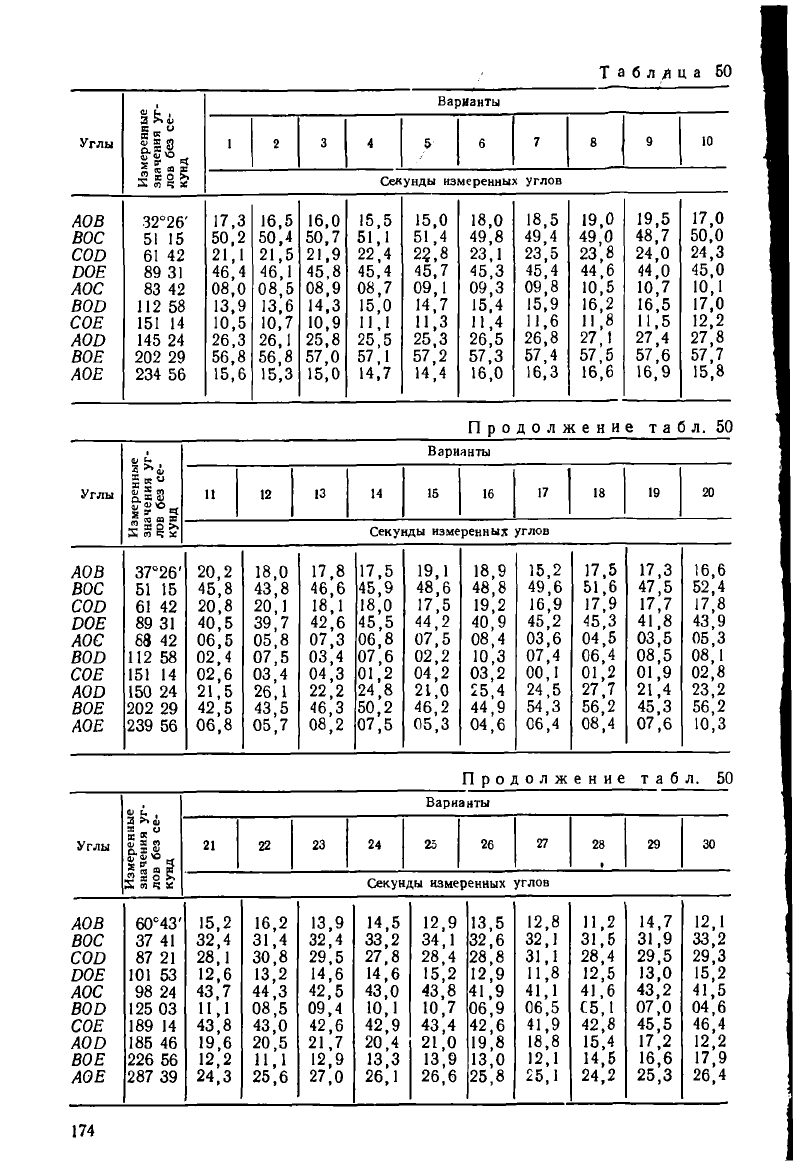
Таблица 54'

Я Б*» О»

Варианты

Я Б*» О»

Углы

а*|

1 2

9 10

3. я ч а:

Секунды измеренных углов

АОВ

ВОС

СОй

йОЕ

АОС

ВОО

СОЕ

АОй

ВОЕ

АОЕ

32°26'

51 15

61 42

89 31

83 42

112 58

151 14

145 24

202 29

234 56

17.3

50.2

21,1

46.4

08,0

13,9

10.5

26.3

56,8

15.6

16,5

50.4

21.5

46,1

08.5

13.6

10.7

26,1

56.8

15,3

16,0

50.7

21,9

45.8

08.9

14,3

10,9

25,8

57,0

15,0

15,5

51,1

22,4

45.4

08,7

15.0

11.1

25.5

57,1

14.7

15.0

51,4

23,8

45,7

09.1

14,7

11,3

25.3

57.2

14.4

18,0

49,8

23,1

45,3

09.3

15.4

11.4

26.5

57,3

16,0

18,5

49.4

23.5

45,4

09.8

15.9

11.6

26,8

57,4

16,3

19,0

49.0

23,8

44,6

10,5

16,2

11,8

27.1

57.5

16.6

19,5

48,7

24,0

44,0

10,7

16,5

11.5

27,4

57.6

16,9

17,0

50,0

24,3

45.0

10.1

17,0

12,2

27,8

57.7

15.8

Продолжение табл. 50

" 4.

Варианты

Углы

л ^

г §

13 14 15

18 19

Секунды измеренных углов

АОВ

ВОС

СОИ

ИОЕ

АОС

ВОй

СОЕ

ДОО

ВОЕ

АОЕ

37°26'

51 15

61 42

89 31

68 42

112 58

151 14

150 24

202 29

239 56

20,2

45,8

20,8

40,5

06.5

02.4

02.6

21.5

42,5

06,8

18,0

43,8

20,1

39.7

05.8

07,5

03.4

26,1

43.5

05,7

17,8

46,6

18,1

42,6

07.3

03.4

04,3

22,2

46,3

08,2

17,5

45,9

18,0

45.5

06,8

07.6

01,2

24,8

50,2

07,5

19.1

48,6

17,5

44.2

07,5

02,2

04,2

21,0

46.2

05.3

18,9

48.8

19.2

40.9

08,4

10.3

03,2

25.4

44,9

04,6

15,2

49,6

16,9

45.2

03,6

07.4

00,1

24.5

54.3

06.4

17.5

51.6

17,9

45.3

04,5

06.4

01,2

27.7

56,2

08,4

17.3

47,5

17.7

41.8

03,5

08.5

01.9

21.4

45,3

07.6

16,6

52,4

17.8

43.9

05,3

08,1

02,8

23,2

56.2

10.3

П р о д о л ж

е н и е табл. 50

Варианты

2 о.

Углы

ах!!

а 9

21 22

23 24

•

29 30

Д Зой

5 я ч х

Секунды измеренных углов

АОВ

ВОС

СОй

ЮОЕ

АОС

ВОО

СОЕ

АО О

ВОЕ

АОЕ

60°43'

37 41

87 21

101 53

98 24

125 03

189 14

185 46

226 56

287 39

15.2

32,4

28,1

12,6

43.7

11,1

43.8

19,6

12,2

24.3

16,2

31.4

30,8

13.2

44.3

08.5

43.0

20.5

11.1

25.6

13,9

32.4

29.5

14.6

42.5

09,4

42.6

21.7

12,9

27,0

14.5

33.2

27.8

14.6

43.0

10.1

42.9

20,4

13.3

26,1

12,9

34.1

28,4

15.2

43.8

10,7

43,4

21,0

13.9

26,6

13.5

32.6

28,8

12,9

41,9

06,9

42,6

19,8

13,0

25,8

12,8

32,1

31,1

11,8

41,1

06,5

41,9

18,8

12,1

25,1

11,2

31,5

28.4

12.5

41.6

СБ,

42,8

15.4

14.5

24,2

14,7

31,9

29,5

13,0

43,2

07,0

45.5

17.2

16.6

25.3

12,1

33.2

29.3

15,2

41.5

04.6

46.4

12,2

17,9

26,4

174

Таблица

172

Номера

тре-

угольников

Номера

углов

Измеренные

значения

уг-

лов (без се-

кунд)

Номера

тре-

угольников

Номера

углов

Измеренные

значения

уг-

лов

(без се-

кунд)

Номера

тре-

угольников

Номера

углов

Измеренные

значения

уг-

лов

(без се-

кунд)

33'

I 2 60

III

9 60

Таблица

Варианты

Секунды измеренных углов

31.5

12.6

20,1

36,5

19.8

07.9

53,8

22,5

41,3

30.2

10.5

18.3

38.2

18.6

09.3

52,5

24,1

40,3

28,5

09,3

17.1

34,9

20,1

08.2

51,7

23,0

42,2

32.0

10.1

22.4

33,2

17.5

05,5

50,9

24,1

38,5

29.4

08.5

17.4

35.2

18,9

10.3

42.5

26.6

43,2

27,3

10,2

16,5

34.3

19.5

11,8

45,2

21.4

42.6

32.1

12.2

22,4

30.1

17,8

09,0

47,3

21,3

44.2

25,6

15,3

32,8

16,5

14,3

46,2

20,5

45,1

26.7

17.8

18,8

34,3

19.2

15.1

46,8

25.3

43.2

30.2

18.4

19.3

31,2

17.5

08,1

43.4

29.2

42.3

28,1

16,4

18,6

30.1

15.2

07.3

45,6

22,3

44.9

3.30.

нивелирной сети, содержащей одну узловую Уочку

(рис. 49),

изме-

рены превышения

1,368;

4,694;

—0,905. Найти уравненное

зна-

чение отметки узлового репера

и ее вес,

если длины ходов примерно одинаковы,

а отметки исходных марок

189,617;

186,292;

191,880.

3.31. Даны уравнения поправок

V =

ЛДл:+

I, где

матрица

1 -1,50 \

Л=

0 2,10 ,

0,7 -2,17 )

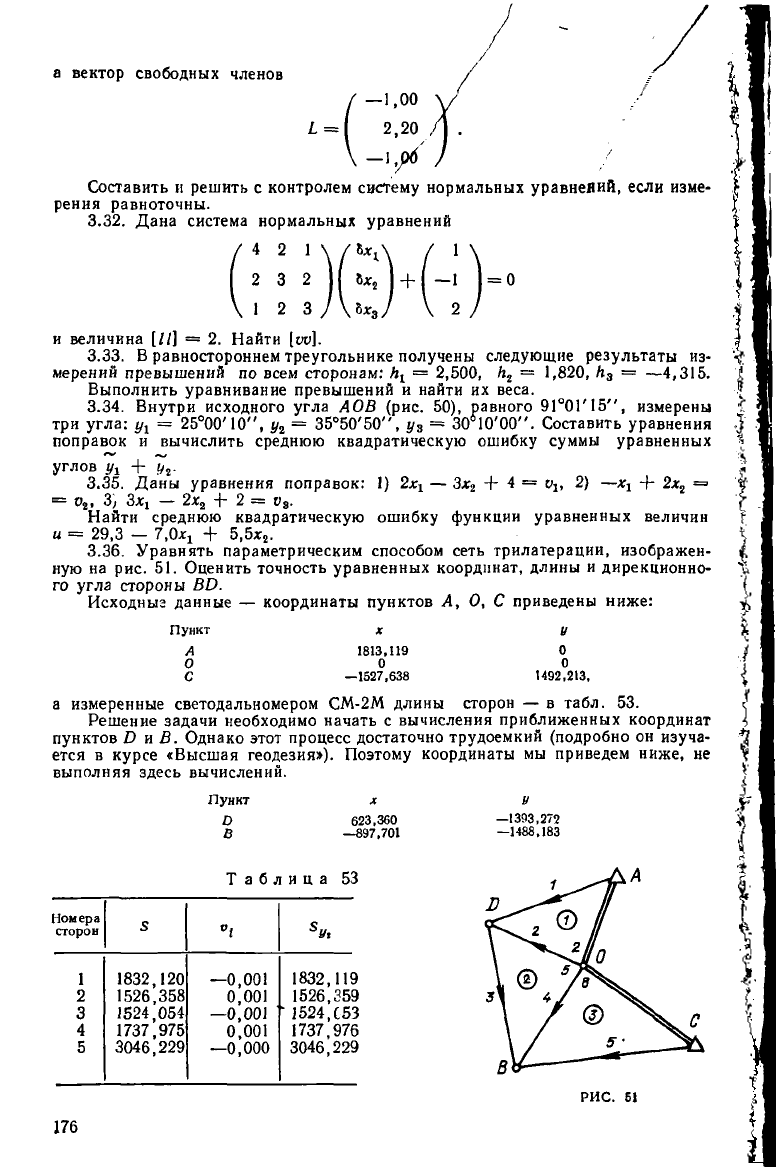
а вектор свободных членов

/ -1,00

I = I 2,20

\ -1.У

Составить и решить с контролем систему нормальных уравнеяий, если изме-

рения равноточны.

3.32. Дана система нормальных уравнений

и величина [//] = 2. Найти (от].

3.33. В равностороннем треугольнике получены следующие результаты из-

мерений превышений по всем сторонам: Н

= 2,500, Н

= 1,820, Н

= —4,315.

Выполнить уравнивание превышений и найти их веса.

3.34. Внутри исходного угла АОВ (рис. 50), равного 91°0Г15", измерены

три угла: у

= 25°00'10", у

= 35°50'50", у

= 30

10'00". Составить уравнения

поправок и вычислить среднюю квадратическую ошибку суммы уравненных

углов у

+ у

3.35. Даны уравнения поправок: 1) 2х

— 3*

+ 4 = 2) —х

+ 2х

= 0

!Р

3; 3*! — 2х

+ 2 = V

Найти среднюю квадратическую ошибку функции уравненных величин

и = 29,3 — 7,0*! + 5,5*

3.36. Уравнять параметрическим способом сеть трилатерации, изображен-

ную на рис. 51. Оценить точность уравненных координат, длины и дирекционно-

го угла стороны ВО.

Исходныг данные — координаты пунктов А, О, С приведены ниже:

Пункт

1813,119

-1527,638

1492,213,

а измеренные светодальномером СМ-2М длины сторон — в табл. 53.

Решение задачи необходимо начать с вычисления приближенных координат

пунктов О и В. Однако этот процесс достаточно трудоемкий (подробно он изуча-

ется в курсе «Высшая геодезия»). Поэтому координаты мы приведем ниже, не

выполняя здесь вычислений.

Пункт

623,360

—897,701

—1393,27?

—1488,183

Таблица 53

Номера

сторон

1832,120

1526,358

1524,054

1737,975

3046,229

1 1

о о о о о

О О ООО

о о о о о

1832,119

1526,359

"1524,С53

1737,976

3046,229

РИС. 51

176.

Таблица 54'

Номера

сторон

СОЗ з!п а

лх<°>

Д»<°>

о (о)

229°30'

294 06

183 34

238 54

281 56

—0,649

0,408

—0,998

—0,517

0,207

—0,760

—0,913

—0,062

—0,856

—0,978

—1189,759

623,360

— 1521,061

—897,701

629,937

—1393,272

—94,911

—1488,183

—2980,396

1832,139

1526,363

1524,019

1737,975

3046,240

1. Составление уравнений поправок.

Как было получено в задаче 3.2, эти уравнения имеют вид

Щ = — соза

6л:

нач

— зш а*8у

нач

+ соз а

кон

+ зт а^(/

кон

= +(3.58>

если стороне I придать направление с начального пункта к конечному. Необхо-

димые для вычисления коэффициентов созя; и 81па

дирекционные углы с точ-

ностью до минут возьмем из задачи 3.27. Вычисления расположим в табл. 54.

Приближенные длины сюрон 5|

вычислены по формуле

3® = + Д.Г

на миникомпьюторе без промежуточных записей. Свободные члены

находят по формуле Ц = — 5

2. Составление нормальных уравнений и их решение дано в табл. 55—57.

Еще раз покажем подробно на числах, как вычисляются весовые коэффици-

енты 0.п\

<?41 = 1/[Л2.3] = 0,629;

= 0,629(—0,3879) <= —0,244;

<Э

=0,629(—0,0022) + (—0,244) (—0,0373) =0,008;

<?41

=0,629X0,0391 + (—0,024) (0,6288 + 0,008(—0,1149) 0,130;

контроль:

(—0,062) (—0,130) + (—0,004)0,008+0,302(—0,244) + 1,693X0,629=0,999,

(?зз= 1,4749+ (—0,244) (—0,3879) = 1,570,

<?32= (—0,244) (—0,0022) + !,570(—0,0373)=—0,058,

Таблица 55-

Номера

изме-

рений

—0,649

0,408

0,998

1,667

—0,001

—0,760

—0,913

0,062

1,210

0,002

—0,998

—0,517

0,207

—1,722

0,001

—0,062

—0,856

—0,978

0,878

1,9

0,5

-3,5

1.1

0,491

—0,005

—3,500

—1,373

0,329

[то] =

[IV] =

—0,101

0,075

—0,097

0,139

—0,115

0,058

0,059

177

Таблица 54'

а]

Ь]

с]

[в

1,584

0,182

—0,996

—0,062

—4,522

—3,814

1,414 —0,062 —0,004

-2,118

—0,588

[с

1,306

0,302

3,721

4,271

[Л

1,693

—0,858 '

1,070

17,230

13,524

[»

14,484

<Эл •=

(—0,244) (0,0391) +1,510X0,6288+ (—0,058) (0,1149)= 0,984;

контроль: —0,996X0,984 (0,058) (—0,062) +1,570Х 1,306+ (—0,244) 0,302 = 1,000,

<Э

=0,718+-(—0,058) (—0,0373)+0,008(—0,0022) =0,720,

<Э

= 0,720 (—0,1149) + (—0,058)0,6288+0,008X0,391 =—0,119;

контроль:

0,182 (—0,119) +1,414X0,720+ (—0,062) (—0,058) + (—0,004) (0,008) = 1,000,

<?„ =

0,631

+ (—0,119) (—0,1149) +0,984X0,6288+0,130X0,0391 = 1,258;

контроль:

1,584 X 1,258 + 0,182(—0,119) + (—0,996) 0,984 + (—0,062)(—0,130) =

- 0,999.

Напомним, что вычисляются числа только в нижней части таблицы, верхняя

часть заполняется симметрично нижней.

Составление нормальных уравнений можно выполнить, минуя традицион.

ную схему. В самом деле, если уравнение поправок (3.58) записать в виде

где матрица = (соза^та^, а

-(::)•

го получим для каждой стороны матрицу

/С05 оЛ , , / соз^а, созв1з1па/\ „„

сс= . созо^па, = ' . 3.59)

2x2 \51П<Х|/ \$1паусозс^ зш'а^ /

Матрицу коэффициентов нормальных уравнений, представив «а в блочном

виде порядка к, где к — число определяемых пунктов, получим по форму-

лам [7]:

1) диагональные блоки

(3.60)

178

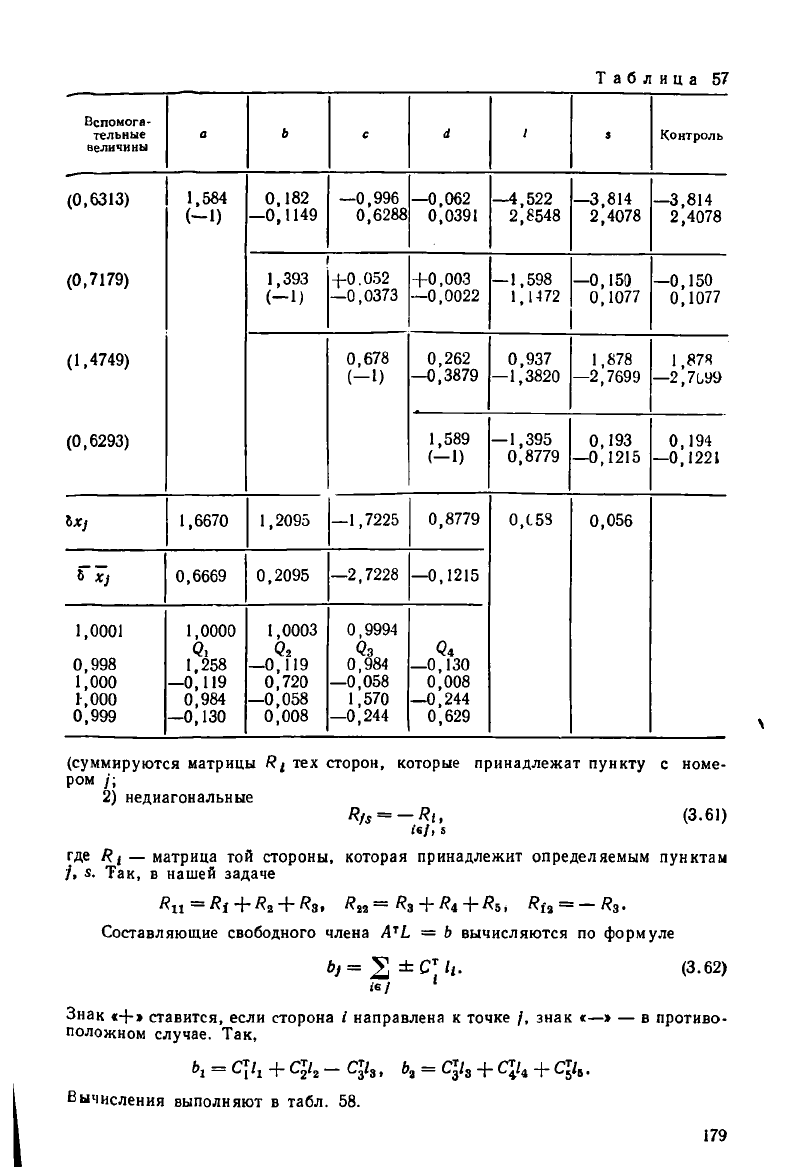
Таблица 54'

Вспомога-

тельные

величины

а ь

Контроль

(0,6313)

1,584

(-1)

0,182

—0,1149

—0,996

0,6288

—0,062

0,0391

—4,522

2,8548

—3,814

2,4078

—3,814

2,4078

(0,7179)

1,393

(-0

-(-0.052

—0,0373

+0,003

—0,0022

—1,598

1,1472

-0,150

0,1077

—0,150

0,1077

(1,4749)

0,678

(-1)

0,262

-0,3879

0,937

—1,3820

1,878

—2,7699

1,878

—2,7Ь99

(0,6293)

1,589

(-1)

—1,395

0,8779

0,193

—0,1215

0,194

—0,1221

Ъх] 1,6670

1,2095

—1,7225

0,8779 0,153

0,056

Ь X]

0,6669

0,2095

—2,7228

—0,1215

1,0001

0,998

1,000

0,999

1,0000

С.

1,258

—0,119

0,984

—0,130

I,0003

—0,119

0,720

—0,058

0,008

0,9994

<?з

0,984

—0,058

1,570

—0,244

<?4

—0,130

0,008

—0,244

0,629

(суммируются матрицы тех сторон, которые принадлежат пункту с номе-

ром /;

2) недиагональные

= —(3.61)

16/, 5

где — матрица той стороны, которая принадлежит определяемым пунктам

/, Так, в нашей задаче

Яц = + + ^з» = +/?4 +/?

— Яз-

Составляющие свободного члена А

Ь = Ь вычисляются по формуле

Ь}=%±С

11. (3.62)

Ы '

Знак «+» ставится, если сторона / направлена к точке /, знак «—» — в противо-

положном случае. Так,

ь,

с*/,

+ - сцз,

сцз

с*/

+ .

Вычисления выполняют в табл. 58.

179

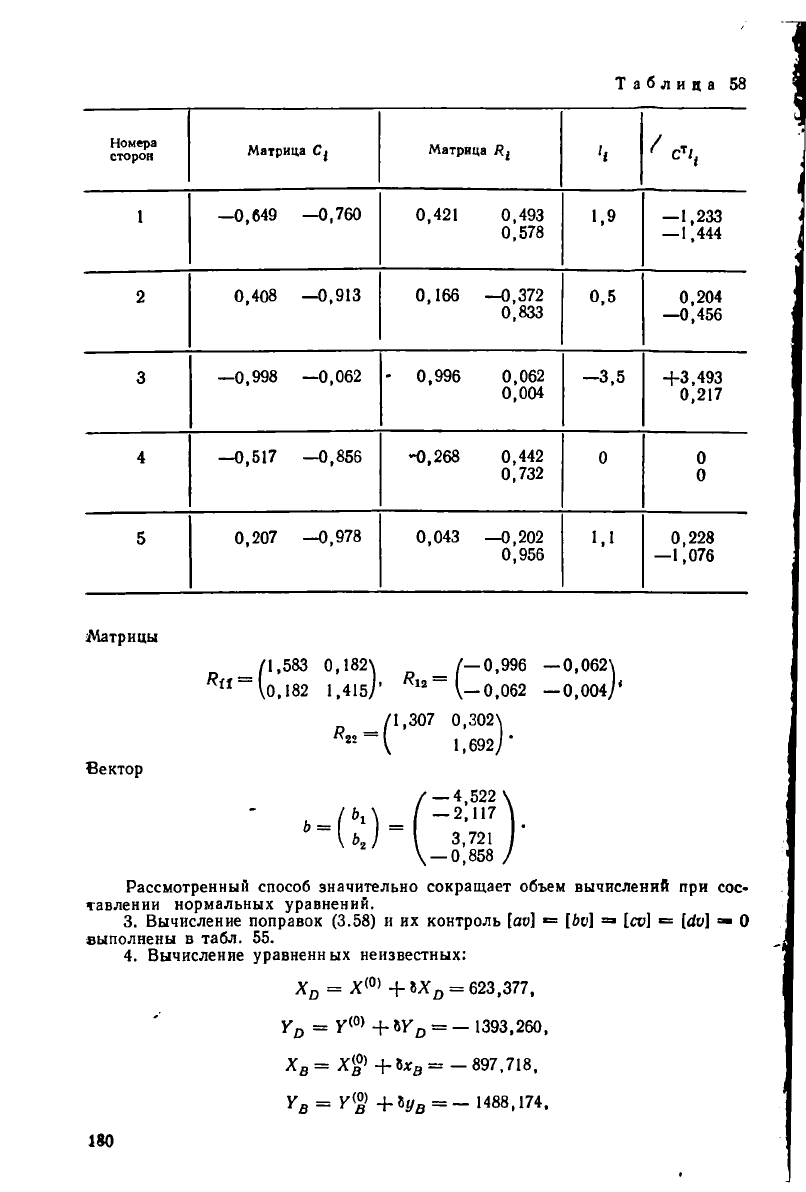
Таблица 64

Номера

сторон

Матрица С{ Матрица

—0,649 —0,760

0,421 0,493

0,578

1,9

—1,233

—1,444

0,408 —0,913 0,166 —0,372

0,833

0,5 0,204

—0,456

—0,998 —0,062 - 0,996 0,062

0,004

-3,5

+3,493

0,217

—0,517 —0,856 'О,268 0,442

0,732

0 0

0,207 —0,978

0,043 —0,202

0,956

1,1

0,228

—1,076

Матрицы

/1,583 0,182\ _ /—0,996 — 0,062\

*"~\0,182 1,415/'

~ (-0,062 -0,004,1'

/1,307 0,302\

1,692]'

Вектор

— 4,522

-2,117

3,721

(

—0,858

Рассмотренный способ значительно сокращает объем вычислений при сос-

тавлении нормальных уравнений.

3. Вычисление поправок (3.58) и их контроль [т] «= [6о] =» [со] «= [&»] =• 0

выполнены в табл. 55.

4. Вычисление уравненных неизвестных:

= Х<°> + ЬХ

= 623,377,

= У

(0)

+ ЬУ

= — 1393,260,

*в= -897,718,

^ в

= =—

1488,174,

180

Таблица

54'

Номера

)

сторон [

Д Ух

Номера

сторон

А*,

—1189,742

623,377

—1521,095

—1393,260

—94,914

1832,119

1526,359

1524,053

—897,718

629,920

—1488,174

—2980,387

1737,976

3046,228

5. Окончательный контроль решения задачи

= /

Д*?

Д</*

где

51, АдС| и Ду

—

соответственно уравненные длины сторон

(см.

табл.

53) и

уравненные приращения координат. Вычисления представлены

табл.

59.

Как видно, задача решена верно.

6. Оценка точности функций.

Коэффициенты ^функции—уравненной длины стороны

Вй

совпадают

коэффициентами уравнения поправок

для

этой стороны,

т. е.

матрица

(0,993 0,062

—

0,998

—

0,062).

Для того чтобы получить матрицу

/ для

второй функции

—

уравненного

дирекционного угла этой стороны, необходимо вычислить коэффициенты уравне-

ния поправок

для

дирекционного угла

(см.

задачу

3.3).

Поэтому будем иметь

р"/5

(з1п

— соз а

—

зт

соз

)

или,

так как

р"/5

206265/1524=

1,353

• Ю

=(— 0,084+

1,350

+0,084

—

1,350)

• Ю

по

формуле (3.49) находим матрицу

= При

этом

( 0,998 0,062

—

0,998

—

0,062

~ V—0.084.Ю

1,350-Ю

0,301-Ю

—0,848-10^

(

1,258 —0,119 0,984 —0,130>

—

0,119

0,720

—

0,058 0,008

0,984

—

0,058

1,570

—

0,244

— 0,130 0,008

—

0,244 0,629^

0,274

— 0,017 —

0,573 0,075

~~ V— 0,008-Ю

0,966

• Ю

0,301 • 10

—

0,848

• Ю

_/ 0,840

—

0,195

• Ю

и ^_

0]9б

-2 2,475-

К)

Так

как в

нашей задаче число избыточных измерений

г = п — к = 5 — 4=

недостаточно, чтобы можно было вычислить среднюю квадратическую ошибку

измерения,

то

невозможно вычислить

ошибки

функций. Однако большой

опыт измерений позволяет считать известным среднее квадратическое отклонение

0,02 м.

Для координат пунктов имеем

181

Таблица 54'

Номера

сторон

Измеренные

дирекционные

углы

Секунды

уравненных

дирекционных

углов

Номера

сторон

Измеренные

дирекционные

углы

Сек нды

уравненных

дирекционных

углов

229°30'15,9"

294 06 16,5

183 34 09,2

15,9

16,6

09,2

238 54 02,2

281 56 06,8

02,2

06,8

=0,02/1,258 = 0,022 м,

= 0,02 /0,720 =0,017 м,

=0,02/1,570 =0,025 м,

Ув

=0,02 /0,629 =0,016 м,

а для функций

о =о

= 0,02 /0,840 =0,018 м, а/5 = 1/85000,

ГI о

о/

а =о 0,02 / 2,475- Ю

=3,1".

Рг «я

3.37. Уравнять параметрическим способом сеть (см. рис. 52), в которой бы-

ли измерены гиротеодолитом дирекционные углы (результаты измерений приве-

дены в табл. 60). Оценить точность тех же элементов сети, что и в задаче 3.36.

Решение. 1. Полагая известными приближенные координаты пунктов

О и С (см. задачу 3.36), составляем уравнение поправок для дирекционных углов

сторон (см. задачу 3.3)

Р"

Щ = (51П а,8*

нач

— соз а^да, — зш а

®*

кон

+ соз я

6</

нач

+ I,),

где свободный член

(0) (0) ,

= а

—

(XI,

а а, = агс1§

д*<°>

Вычисления располагаем в табл. 61.

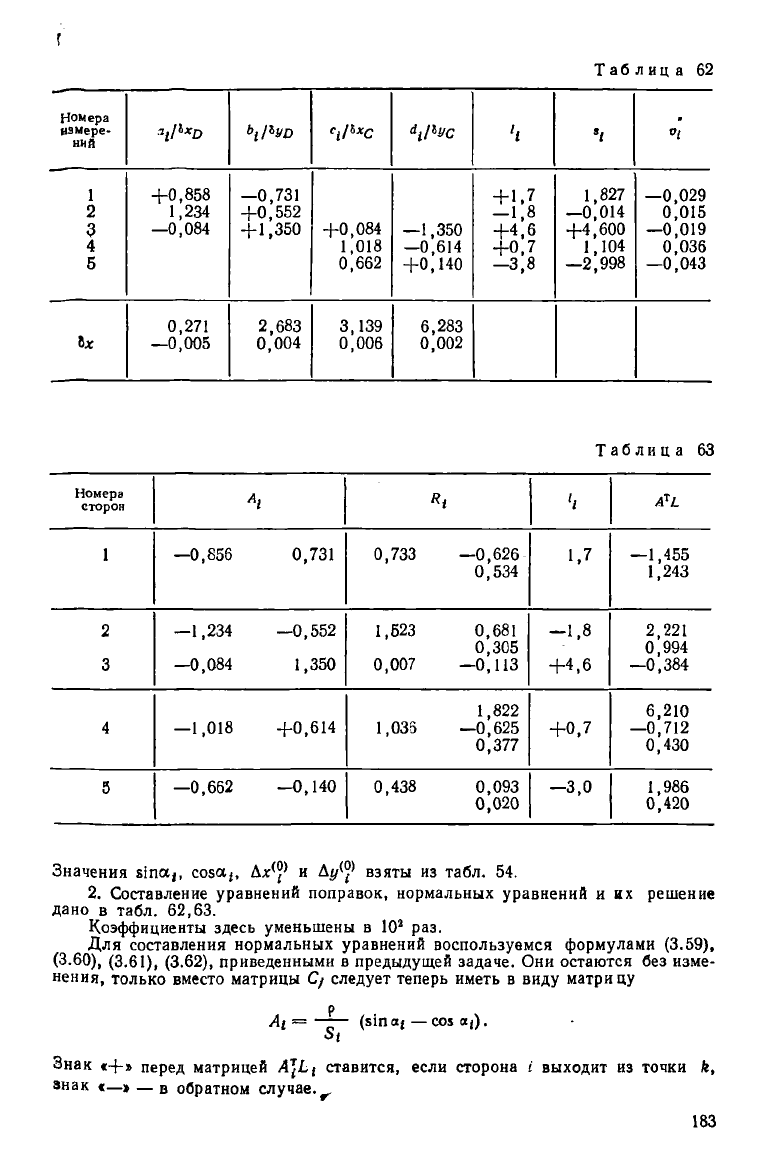
Таблица 61

Номера

сторон

V;,

узШ а

--со* а

1832

1526

1524

1738

3046

—0,656- Ю

—1,234

—0,084

—1,018

-0,662

0,731•10

—0,552

+ 1,350

+0,614

—0,140

1,171054

—2,2351001

0,0623979

1,6577714

—4,7312604

229°30'17,8"

294 06 14,7

183 34 13,8

238 54 02,9

281 56 03,8

182

Таблица 54'

Номера

измере-

ний

{

/Чо

Ьх

УС

+0,858

1,234

—0,084

—0,731

+0,552

+1,350

+0,084

1,018

0,662

—1,350

-0,614

+0,140

+ 1,7

-1,8

+4,6

+0,7

—3,8

1,827

—0,014

+4,600

1,104

—2,998

—0,029

0,015

—0,019

0,036

—0,043

Ьх

0,271

—0,005

2,683

0,004

3,139

0,006

6,283

0,002

Таблица 63

Номера

сторон

1 «1

АЧ

—0,856 0,731

0,733

—0,626

0,534

1,7

—1,455

1,243

-1,234

-0,084

—0,552

1,350

1,523

0,007

0,681

0,305

—0,113

-1,8

+4,6

2,221

0,994

—0,384

—1,018

+0,614

1,035

1,822

—0,625

0,377

+0,7

6,210

—0,712

0,430

—0,662 -0,140

0,438

0,093

0,020

-3,0 1,986

0,420

Значения з1па,, сова^, Длг

(

®' и Ду^ взяты из табл. 54.

2. Составление уравнений поправок, нормальных уравнений и их решение

дано в табл. 62,63.

Коэффициенты здесь уменьшены в 10

раз.

Для составления нормальных уравнений воспользуемся формулами (3.59),

(3.60), (3.61), (3.62), приведенными в предыдущей задаче. Они остаются без изме-

нения, только вместо матрицы С/ следует теперь иметь в виду матри цу

А[ = —— (МПа{—С05 0|).

Знак «+» перед матрицей Аставится, если сторона !' выходит из точки к,

знак «—» — в обратном случае.

183