Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Свободные члены выражены в сантиметрах.

Веса измерений вычисляем по формуле = 40//.

В табл. 85 и 86 приведены коэффициенты уравнений поправок и нормальных

уравнений.

В качестве оцениваемых функций выбраны превышения по ходам 1 и 5.

Для первой функции Р

коэффициенты — 1, /

= 0, /

= 0, для второй Д — О,

/а = 1, /з = —1. В столбце 2 табл. 86 два последних числа равны соответственно

1Л1 = 1 и 1/1, = 0.

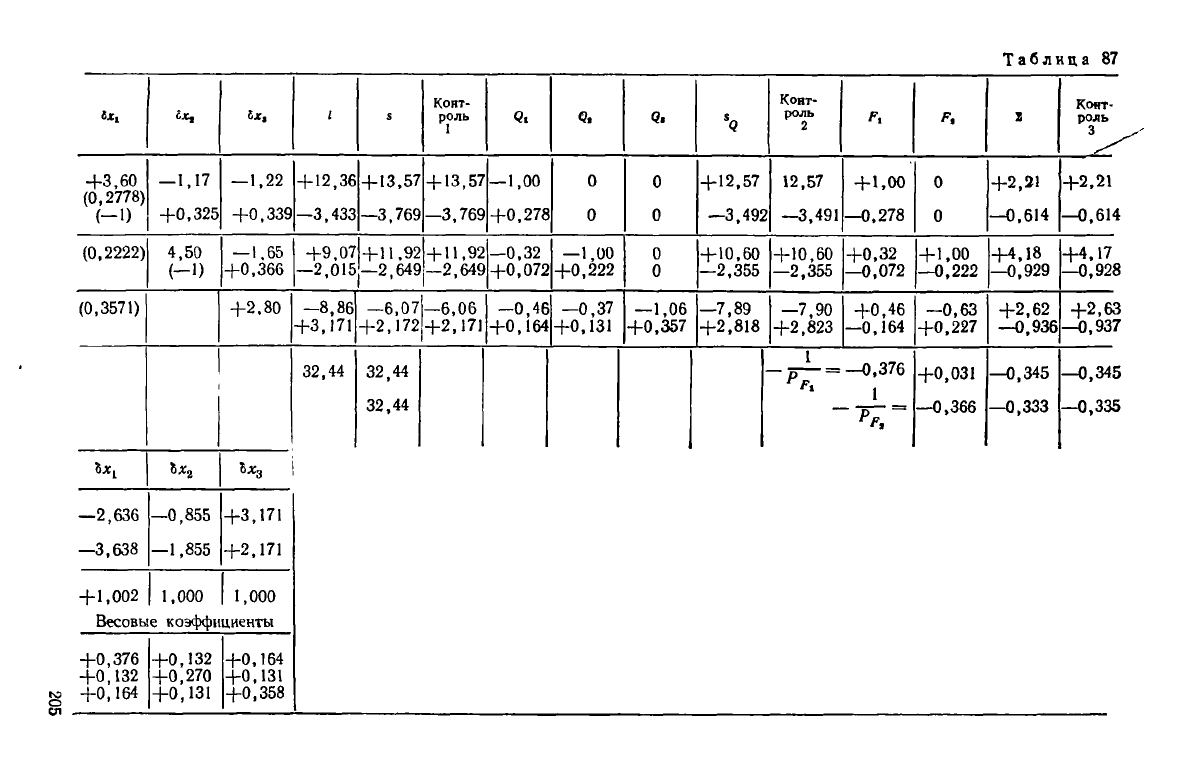
Решение системы нормальных уравнений приведено в табл. 87.

В результате проведенного решения получены следующие значения неиз-

вестных:

= 189,641 м —2,64 см = 189,615 м:

= 197,967 м —0,85 см = 197,959 м;

= 190,950 м + 3,17 см = 190,981 м.

Средние квадратические ошибки единицы веса и на 1 км хода равны:

Г 32,42 „

=2,85 см; «км = = 0,45 см.

/40

Вес последнего неизвестного равен

Р = -7— = 2,80.

Чэз

Вес первого неизвестного получен дважды

Р =Т- = 2,65, р

= —^ = 2,65.

Вес предпоследнего неизвестного

ГрЬЬ. 11 1

Р = тР =3,70, р = — = 3,70.

Ч [рсс. Ц Ч (}

гг

Средние квадратические ошибки:

УОа =2,85 У/ 0,376 = 1,75 см,

"V.

Х1

= ц = 2,85 у 0,270 = 1,48 см,

= УОм = 2,85 /0,358 = 1,70 см,

{Х

-у/"у- = 2,85 /о7376~= 1,75 см,

, = ц у- = 2,85 V0,366' = 1,72 см.

"V,

После введения поправок в измеренные величины получим

Л, = + 6,108

м, й

= + 8,343

М,

= -Ь 5,605

м, \ = + 1,367

М,

Л, = — 6,976, м, "Н

= — 898

м, Л, = + 6,078

м.

204.

Таблица

105

«1

Ьх,

Конт-

роль

0. <?.

<з

Конт-

роль

г,

Р,

Конт-

роль

+3,60

(0,2778)

(-1)

—1,17

+0,325

—1,22

+0,339

+12,36

—3,433

+ 13,57

—3,769

+ 13,57

—3,769

— 1,00

+0,278

+ 12,57

—3,492

12,57

—3,491

+1,00

—0,278

+2,21

—0,614

+2,21

—0,614

(0,2222)

4,50

(-1)

— 1,65

+0,366

+9,07

—2,015

+ 11,92

-2,649

+ 11,92

—2,649

—0,32

+0,072

—1,00

+0,222

+10,60

—2,355

+10,60

—2,355

+0,32

—0,072

+1,00

—0,222

+4,18

—0,929

+4,17

—0,928

(0,3571)

+2,80

-8,86

+3,171

—6,071—6,06

+2,172+2,171

—0,46

+0,164

-0,37

+0,131

—1,06

+0,357

—7,89

+2,818

—7,90

+2,823

+0,46

-0,164

—0,63

+0,227

+2,62

—0,936

+2,63

—0,937

32,44 32,44

32,44

-0,376

Л ~

+0,031

—0,366

—0,345

—0,333

—0,345

—0,335

Ьх

—2,636

—3,638

—0,855

—1,855

+3,171

+2,171

+ 1,002 | 1,000 | 1,000

Весовые коэффициенты

+0,376

+0,132

+0,164

+0,132

+0,270

+0,131

+0,164

+0,131

+0,358

—

Окончательным контролем правильности решения задачи является ^ыполненве

равенства = х

кон

— х

нач

для каждого хода сети. >

Способ узлов проф. В. В. Попова для составления нормальных

уравнений

Для случая уравнивания нивелирных сетей и углов в сети полигоно-

метрии проф. В. В. Попов предложил следующие правила составле-

ния нормальных уравнений с помощью чертежа сети:

а) квадратичные коэффициенты нормальных уравнений в строке

/ равны сумме весов ходов, сходящихся в узле с тем же номером /;

б) неквадратичные коэффициенты, расположенные в строке / и

столбце Н, равны отрицательному весу хода, соединяющего узлы с но-

мерами / и Н\

в) свободные члены нормальных уравнений получаются суммиро-

ванием величин ±р^1 тех ходов, которые сходятся в узле /, причем

если узел является конечной точкой хода, то ставится знак «+», а

если начальной, то «—

Например, для нивелирной сети (см. рис. 56) нормальные уравне-

ния будут

(Р1 + Р2 + Рь) —

— р$х

+ ^ = 0;

— р

Ьх

+ (р

+ р

+ р,) 5*2 — Ръ

Ьх

з + Ь

= 0;

— р

Ьх

— р

Ьх

+ (р

+ р

) Ьх

+ Ь

= 0,

а свободные члены

К =М —Ргк —РА!*>

= р

—/Уз —Рък +

Рч

т>

= Рьк + Ръ

ь + Рв

в-

Указанные правила тождественны следующим формулам состав-

ления матрицы системы нормальных уравнений (3.72)1 ее диаго-

нальные элементы

Я» = 2д (3.75)

1е/

(запись / С / означает здесь принадлежность 1-го хода /-му узлу), а

недиагональные

2 ±р, (3.76)

»/. к

(знак суммы предусматривает случай, когда узлы / и к соединены не-

сколькими ходами).

Вектор свободных членов Ь имеет элементы

3.49. Составить по способу В. В. Попова систему нормальных уравнений в

задаче 3.48.

206.

3.50. Выполнить параметрическим способом

уравнивани* сети триангуляции (рис. 57), если

в ней измерены* дирекционные углы

Номера дирекционных

углов

матрица весов которых

Р =

Измеренные значения

229° 30'17,9"

294 Об 17,4

183 34 12,7

238 54 00,7

281 56 01,2,

РИС. 67

Координаты исходных пунктов взять из задачи 3.36.

Исходные дирекционные углы

а , = 0°;

ОА

ов

= 135

Приближенные значения координат определяемых пунктов примем равными

приведенным ниже:

Пункт Р

(0) „(0)

623,360

—897,701

—1393,272

—1488,183

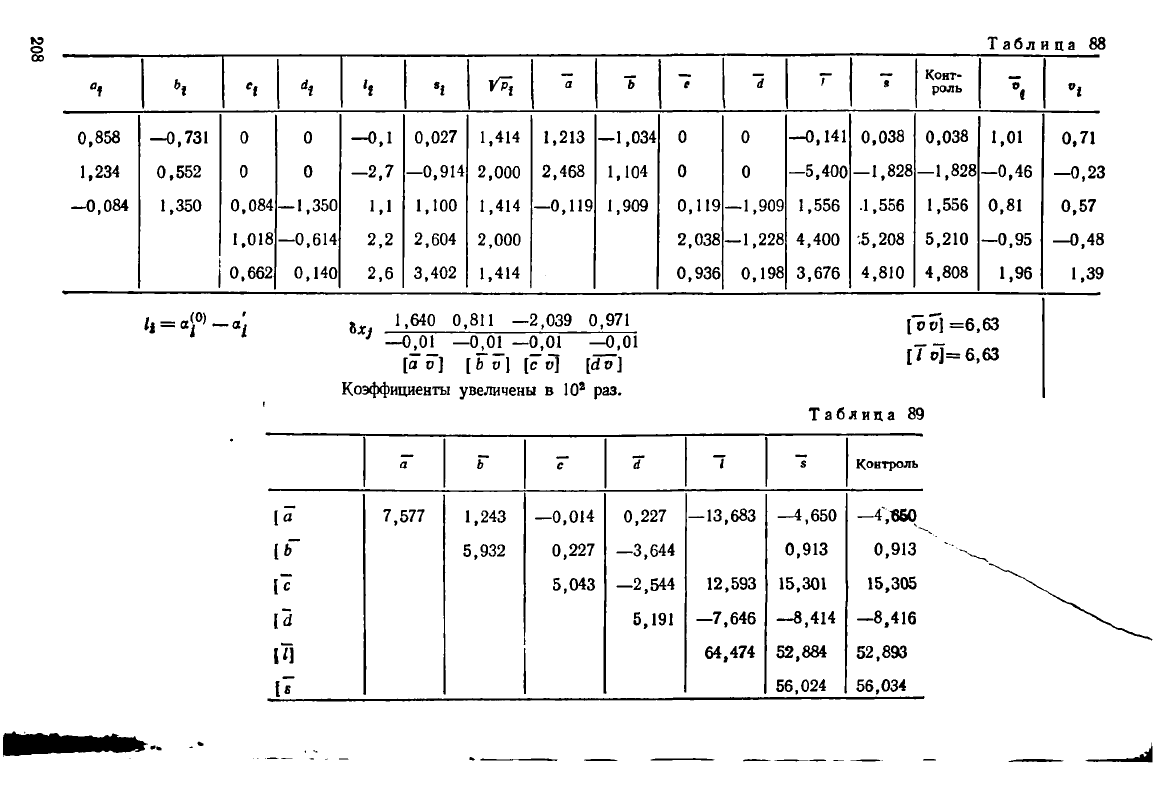
Решение. Эта задача отличается от решенной ранее задачи 3.37 лишь

тем, что теперь дирекционные углы неравноточны**. Таблицы коэффициентов

уравнений поправок и составления нормальных уравнений имеют вид, приве-

денный в табл. 88, 89.

Решение нормальных уравнений и получение матрицы весовых коэффици-

ентов представлено в табл. 90, а вычисление поправок у,, о, = 0{/У~Р1 с контро-

лем [ао] = [М » ... " 0 и [ЪБ] = уТ.к] «= [7в.й] — в табл. 88.

Уравненные значения координат и уравненных дирекционных углов приве-

дены ниже.

Пункт р

Номера дирекционных углов

*(0) „(0)

623,378 —1393,264

—897,721 1488,173

Уравненные дирекционные углы

229°30'18,6"

294 06 17,2

183 34 13,3

238 54 00,2

281 56 02,6

При уравнивании этого построения имеем всего одно избыточное измерение,

поэтому вычислить ошибку единицы веса |х не представляется возможным. Одна-

ко учитывая, что в качестве измеренных углов здесь приняты предварительно

уравненные углы из задачи 3.36, можно применить формулу

[то] = [«>'»'] + [То ] = 35,76 + 6,63 = 42,39,

где через обозначены поправки углов, уравненных в задаче 3.36.

* Здесь в качестве измеренных приняты уравненные в задаче 3.27 дирек-

ционные урлы сторон.

** Почему их веса выбраны именно такими, мы объясним в § 48 (задача 5.27).

207.

Таблица

105

Н Ч

«1

Конт-

роль

0,858

—0,731

0 0

-0,1

0,027

1,414

1,213

—1,034

—0,141

0,038

1,01 0,71

1,234

0,552

0 -2,7

—0,914

2,000

2,468

1,104 0

—5,400

—1,828 —1,828

—0,46

—0,23

—0,084

1,350

0,084

— 1,350

1.1

1,100 1,414

—0,119

1,909 0,119

—1,909

1,556

.1,556

1,556

0,81

0,57

1,018

—0,614

2,2

2,604

2,000

2,038

—1,228

4,400

-.5,208

5,210

—0,95

—0,48

0,662

0,140

2,6

3,402

1,414

0,936

0,198

3,676

4,810

4,808

1,96 1,39

Ьх

1,640 0,811

—2,039

0,971

—ОДИ —<МН

—0,01 —0,01

[а V]

[ Ь

V ] [с о]

[Л

о]

Коэффициенты увеличены

в 10

раз.

[VV]

=6,63

[То]= 6,63

Таблица

ь а

Контроль

[я

7,577

1,243

—0,014 0,227 —13,683

—4,650 —4,660

5,932

0,227 —3,644

0,913 0,913

[с

5,043

-2,544

12,593

15,301

15,305

5,191

—7,646

—8,414

—8,416

64,474

52,884

52,893

56,024 56,034

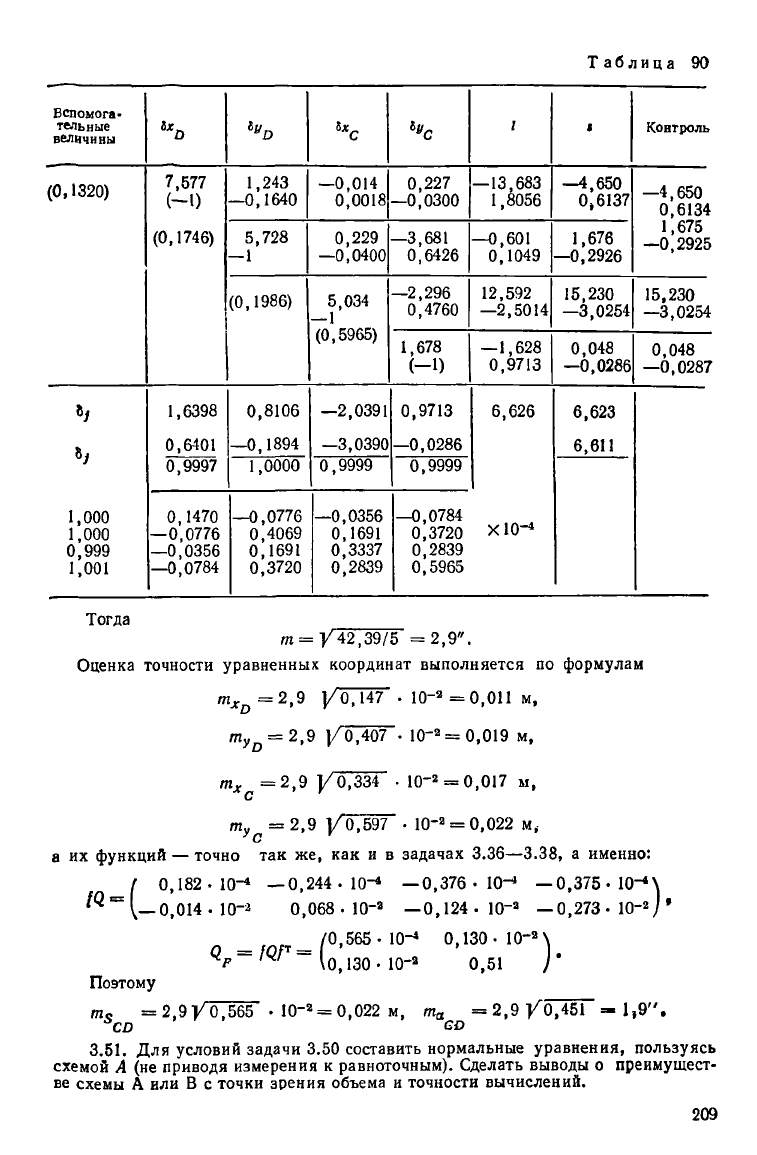
Таблица 81 Таблица 83

Вспомога-

тельные

величины

"о

*С

»с

Контроль

(0,1320)

7,577

(-0

1,243

—0,1640

—0,014

0,0018

0,227

—0,0300

—13,683

1,8056

—4,650

0,6137

—4,650

0,6134

(0,1746)

5,728

—1

0,229

—0,0400

—3,681

0,6426

—0,601

0,1049

1,676

—0,2926

1,675

—0,2925

(0,1986)

5,034

—1

(0,5965)

—2,296

0,4760

12,592

—2,5014

15,230

—3,0254

15,230

—3,0254

5,034

—1

(0,5965)

1,678

(-1)

—1,628

0,9713

0,048

—0,0286

0,048

—0,0287

1,6398

0,8106

—2,0391

0,9713

6,626

6,623

0,6401 —0,1894

—3,0390 —0,0286

6,611

0,9997

1,0000

0,9999

1,000

0,999

1,001

0,1470

—0,0776

—0,0356

—0,0784

—0,0776

0,4069

0,1691

0,3720

—0,0356

0,1691

0,3337

0,2839

—0,0784

0,3720

0,2839

0,5965

Х10"

Тогда

т = У 42,39/5 = 2,9".

Оценка точности уравненных координат выполняется по формулам

=2,9 |/0,147 . 10"

=0,011 м,

Уо

= 2,9 |/0,407 • 10"

= 0,019 м,

т* =2,9 ]/ 0,334 • 10"

= 0,017 м,

т„ = 2,9 1/0,597 • 10'

= 0,022 м,

'с

а их функций — точно так же, как и в задачах 3.36—3.38, а именно:

/ 0,182- 10"

— 0,244. 10"

— 0,376 • 10"

—0,375.10"

0,014 • Ю-з 0,068.10"

— 0,124. Ю"

—0,273 • 10"

о =ю/т=/'

565

°'

13(Ь1(

7 /ч/

\0,130 • Ю

-2

0,51 )'

Поэтому

к, = 2,91/0,565 • 10"

= 0,022 м, т

=2,9/0,451 -1,9".

со со

3.51. Для условий задачи 3.50 составить нормальные уравнения, пользуясь

схемой А (не приводя измерения к равноточным). Сделать выводы о преимущест-

ве схемы А или В с точки зрения объема и точности вычислений.

209

РИС. 58

3.52. Выполнить уравнивание нивелирной сети, изображенной на рис. 58.

Оценить точность всех узловых реперов (матрицу весовых коэффициентов

получить по способу Ганзена) и уравненного превышения Й4. Обратный вес этой

функции вычислить по формуле (3.49) и в дополнительном столбце схемы Гаусса.

Исходные данные приведены ниже, а измеренные превышения и длины ходов

даны в табл. 91. Нормальные уравнения составить дважды: по схеме В и по спо-

собу узлов проф. В. В. Попова.

Номера опорных реперов Высоты опорных реперов, м

I 188,452

II 188,838

III 186,298

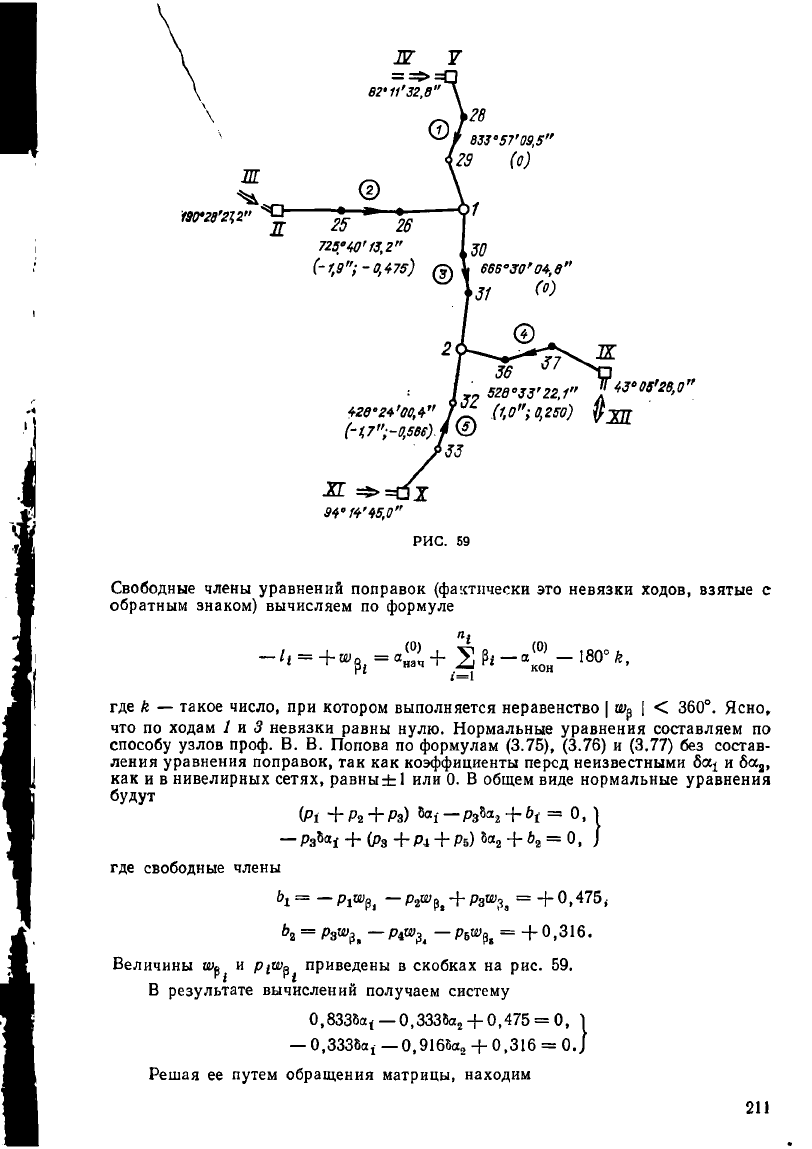
3.53. Выполнить предварительное уравнивание углов в полигонометричес-

кой сети (рис. 59). Оценить точность дирекционных углов узловых направлений,

совпадающих со сторонами 1—30 и 2—32. Суммы измеренных левых углов в

ходах и исходные дирекционные углы на рис. 59 [3].

Решение. Суммы измеренных углов в каждом ходе принимаем в качест-

ве измеренных величин (как и превышения ходов в нивелирной сети). Веса хо-

дов принимаем равными = IIп^ где п

(

— число измеренных углов в каж-

дом ходе. Предполагается, что на узловых точках углы измерены отдельно друг

от друга. Далее вычисляем приближенные значения дирекционных углов сторон

1—30 и 2—32 по ходам / и 3:

196°08'42,3',

= 162°38'47,1".

Таблица 91

Превышения, м

Длина хода, км

Варианты

+2,214+0,001/*

+1,566

—0,302

— 1,881

+0,915

—2,814

—3,137

+ 1,517+0,001/

12,8

14,2

8.7

12,4

5.8

5,1

7,8

10,1

13,4

14,8

9.1

13,0

6,1

5,3

8,3

10,7

14,0

15.5

9.5

13.6

6,4

5.6

8,6

И,1

8,0

8,9

5,4

7,7

3,6

3.2

4,9

6.3

11,1

12,3

7,6

10,7

5,1

4,4

6,8

8,8

11,8

8,0

10,4

5,4

4,8

7,2

9,4

13,2

14,6

8,9

12,8

6,0

5,2

8,1

10,4

15.1

16,7

10.2

14,6

6,9

6,0

9,2

12,0

I — номер шифра студента.

210.

Ш 7

РИС. 59

Свободные члены уравнений поправок (фактически это невязки ходов, взятые с

обратным знаком) вычисляем по формуле

_ I, = + = «<°> + 2 Р« - -

180

где к — такое число, при котором выполняется неравенство | [ < 360°. Ясно,

что по ходам 1 и 3 невязки равны нулю. Нормальные уравнения составляем по

способу узлов проф. В. В. Попова по формулам (3.75), (3.76) и (3.77) без состав-

ления уравнения поправок, так как коэффициенты перед неизвестными бо^ и 6а

как и в нивелирных сетях, равны±1 или 0. В общем виде нормальные уравнения

будут

(Рг + Р

+ Рз) Ч — Рз

*2 + ^ = 0.1

— РзЧ + (Рз+Р4 + Р5)Ч +

а = 0. /

где свободные члены

—

Р1

?г

— + р

и>з

= +0,475,

2 = Рз™

, — Р*®

?А

— = +0,316.

Величины Шр^ и р^^ приведены в скобках на рис. 59.

В результате вычислений получаем систему

0,8338а

— 0,3335а

+0,475 = 0, 1

— 0,3336а

—0,9165а

+ 0,316 = 0./

Решая ее путем обращения матрицы, находим

211

/1,405 0,510\

^ 1,0,510 1,277/

\— 0,646 /

Далее для углов каждого хода вычисляем величины

5а

нач — ®«кон + ^

= 0,83", ^ = -1,07", Ц

= _0,18", 0^=1,65", ^', = 1,05"),

представляющие собой поправки в суммы углов ходов. Контроль вычислений

вытекает из формулы [рай] = [рМ ... = 0 и приобретает вид

2 ± = 0.

Соответственно для узлов 1 к 2 получаем

1) 0,207 — 0,268 + 0,060 = — 0,001,

2)— 0,060 + 0,411 — 0,351 = 0.

Поправки в углы в каждом ходе вычисляем по формуле

(здесь они не приводятся).

Далее по известным формулам вычисляем дирекционные углы всех сторон.

Для оценки точности вычислим величину

[ри>] = [рП.к] = [рЩ + 6

Да =

/—0,828 \

+ (0,475 0,376) (_

0 б4б

) = 2,11 -0,60=1,51".

Средняя квадратическая ошибка измерения одного угла

т = Л/ -г

—^ = О.

'".

ошибка т

= = 0,29",

» 5 — 2

2,51

„„ _ __ 0,71

~ /6"

уравненных дирекционных углов

т., =0,71 ]/1,405 = 0,84", т

а1

= 0,71 ]/1,277 = 0,80".

+ 0,510

Коэффициент корреляции между ними г = .——— = + 0,38.

V 1,405Х 1,277

Если на узлах углы измерены способом круговых приемов, то им следует

приписать вес, равный 2, а всем остальным углам — веса, равные 1. Тогда вес

суммы углов хода с одним узлом найдем, исходя из формулы сГ

1 -I- 1 4- ...

+ 1 + 0,5 = п' — 0,5 = п

и вес

Р =

п' —0,5 «р •

где, как и ранее, п' — число вершин хода, включая узловую точку. Для хода

212

«от узла к узлу» Р

= —;—- . Все вычисления аналогичны выполненным ранее

п —1

с той разницей, что поправки углов на узловых точках вычисляются по формуле

_ _1_ «>з

2 л' — 0,5*

В этом случае получим матрицы

_ / 0,905 —0,333\

~~ 1—0,333 0,905/ '

\0,470 1,278)

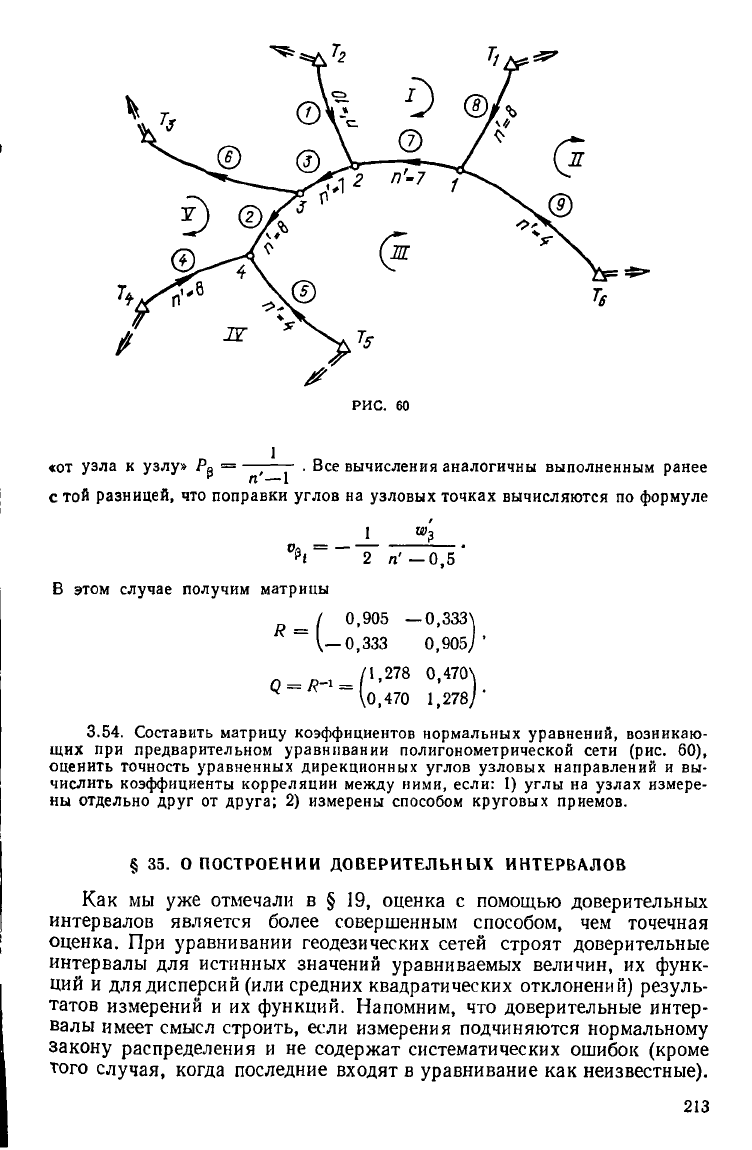
3.54. Составить матрицу коэффициентов нормальных уравнений, возникаю-

щих при предварительном уравнивании полигонометрической сети (рис. 60),

оценить точность уравненных дирекционных углов узловых направлений и вы-

числить коэффициенты корреляции между ними, если: 1) углы на узлах измере-

ны отдельно друг от друга; 2) измерены способом круговых приемов.

§ ЗА. О ПОСТРОЕНИИ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ

Как мы уже отмечали в § 19, оценка с помощью доверительных

интервалов является более совершенным способом, чем точечная

оценка. При уравнивании геодезических сетей строят доверительные

интервалы для истинных значений уравниваемых величин, их функ-

ций и для дисперсий (или средних квадратаческих отклонений) резуль-

татов измерений и их функций. Напомним, что доверительные интер-

валы имеет смысл строить, если измерения подчиняются нормальному

закону распределения и не содержат систематических ошибок (кроме

того случая, когда последние входят в уравнивание как неизвестные).

213.