Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

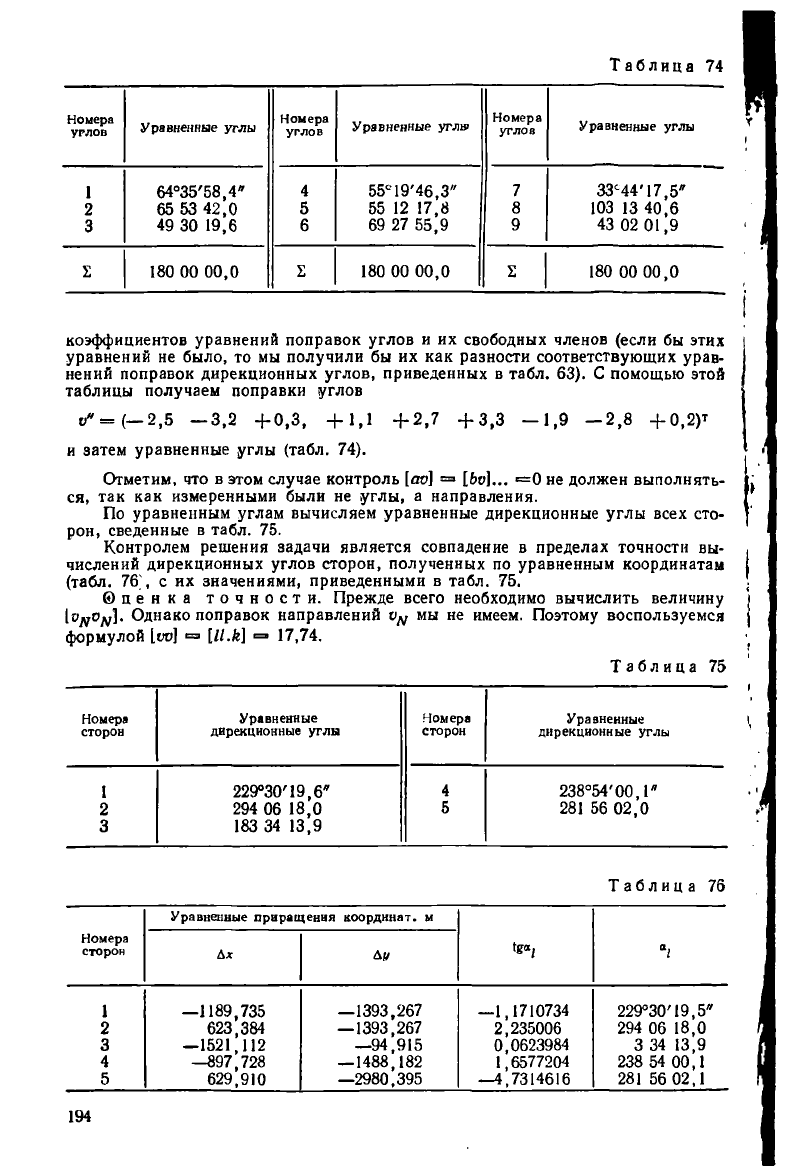
Таблица 81 Таблица 83

Номера

углов

Уравненные углы

Номера

углов

Уравненные угли»

Номера

углов

Уравненные углы

64°35'58,4"

65 53 42,0

49 30 19,6

19'46,3"

55 12 17,8

69 27 55,9

44'17,5"

103 13 40,6

43 02 01,9

X 180 00 00,0

180 00 00,0 2 180 00 00,0

коэффициентов уравнений поправок углов и их свободных членов (если бы этих

уравнений не было, то мы получили бы их как разности соответствующих урав-

нений поправок дирекционных углов, приведенных в табл. 63). С помощью этой

таблицы получаем поправки углов

о*-(-2,5 -3,2 +0,3, +1,1 +2,7 +3,3 -1,9 -2,8 +0,2)*

и затем уравненные углы (табл. 74).

Отметим, что в этом случае контроль [оо] = [6о].„ =0 не должен выполнять-

ся, так как измеренными были не углы, а направления.

По уравненным углам вычисляем уравненные дирекционные углы всех сто-

рон, сведенные в табл. 75.

Контролем решения задачи является совпадение в пределах точности вы-

числений дирекционных углов сторон, полученных по уравненным координатам

(табл. 76^, с их значениями, приведенными в табл. 75.

Оценка точности. Прежде всего необходимо вычислить величину

[о^одр]. Однако поправок направлений мы не имеем. Поэтому воспользуемся

формулой [с®] = [//.&] = 17,74.

Таблица 75

Номера

сторон

Уравненные

дирекционные углы

Номера

сторон

Уравненные

дирекционные углы

229°30'19,6"

294 06 18,0

183 34 13,9

238°54'00,1"

281 56 02,0

Таблица 76

Номера

сторон

Уравненные приращения координат, м

Номера

сторон

Длг

Д#

—1189,735

623,384

—1521,112

—897,728

629,910

—1393,267

—94,915

—1488,182

—2980,395

—1,1710734

2,235006

0,0623984

1,6577204

—4,7314616

229°30'19,5"

294 06 18,0

3 34 13,9

238 54 00,1

281 56 02,1

194

Величина [й] = 42,606 получена по формуле [&] = [а1] + [М] + ... +

+ [/Л.

Алгоритм [/5.&] = 17,76.

Средняя квадратическая ошибка измеренного направления

/ 17,74

14=1г

угла, вычисленного по направлениям, т = 1,9"/2 => 2,7", а уравненных ко-

ординат

= 1,9 /0,575 • 10"

= 0,014 м,

Шу = 1,9/0,631 . 10-

= 0,015 м,

= 1,9 /М95"

•

10"

= 0,018 м,

Шу =1,9 У 1,035 • 10"

= 0,019 м.

Для оцениваемых функций аналогично тому, как было сделано в предыду-

щих задачах, найдем матрицы

_ / 0,507 —0,398 —0,806 —0,627 \ _

\0,318 - 10» 0,111 • Ю-

0,160- 10

— 0,572 • Ю

/' '

Ц.-ГОГ-П'**-

* 0,199-10-

\0,200 • Ю

-2

0,909 )

Средние квадратические ошибки

т$

= 1,9 /17325" • 10"

= 0,021 м,

т = 1,9 /0,909 = 1,8".

3.40. В условиях задачи 3.39 найти матрицу обратных весов приращений

координат по всем сторонам сети.

3.41. Сделать то же самое в условиях задач 3.37 и 3.38.

§ 33. ПРИМЕНЕНИЕ ПАРАМЕТРИЧЕСКОГО СПОСОБА ДЛЯ РЕШЕНИЯ

НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ЗАДАЧ

С применением метода наименьших квадратов тесно связан вопрос

о так называемом сглаживании экспериментальных зависимостей.

Пусть производится опыт, целью которого является исследование

зависимости некоторой физической величины У от физической величи-

ны X, причем предполагается, что У и X связаны функциональной

зависимостью У = ср(Х).

В результате наблюдений получены пары чисел

(«'= 1. 2,..., л).

О форме зависимости судят, исходя из существа задачи, или по

внешнему виду экспериментальной зависимости. Например, экспери-

ментальные точки, изображенные на рис. 53, предполагают прямо-

линейную зависимость вида у = ах + Ь, а на рис. 54 — полином

второй степени у = ах

+ Ьх + с. В общем случае можно говорить

7* 195

• I ' I • -« I I I

О 123456789Х

РИС. 53

РИС. 54

РИС. 55

о подборе полинома степени п—1, который задает кривую, проходя-

щую через все п точек (*/*//). Но построение такого полинома нецеле-

сообразно, ибо существующая закономерность будет искажена слу-

чайными ошибками наблюдений. Для сглаживания случайных укло-

нений как раз и служит метод наименьших квадратов.

С его помощью определяют параметры а, Ь, с сглаживающих поли-

номов. Так, для прямолинейных зависимостей будем иметь уравне-

ния (3.3) вида

Здесь роль неизвестных играют два параметра а и Ь, а роль измерений

— величины у\ коэффициенты при а и Ь образуют матрицы

Поэтому имеем систему нормальных уравнений с двумя неизвест-

ными

ах

+ Ь —

Уг

= V,

ах

+ Ь—у

= V

аx

+ Ь — у

(п> 2).

[#\а + [х\Ь — [ху\=0Л

\х\ а + пЬ — [у] = 0. ]

Решение легко выполнить с помощью обратной матрицы

где

Отсюда

а =

п [ху\ — [х] [у]

(3.66)

196.

_ — [*1 [*у\ + [у] [*

3 б7)

[х*]п — [х]

' '

Таблица 81 Таблица 83

Рассмотрим пример. Пусть имеем пары

наблюдений (хпредставленные в табл. 77

и на графике в виде точек (рис. 55).

Далее вычисляем:

[х

[ = 385, \ху\ = 200,9, [х

] п — [хI

= 325.

График показывает, что можно предпо-

ложить функциональную зависимость у =

= ах + Ь. Согласно формулам (3.66) и (3.67)

имеем

2009-1870

825

, — 11 049,5 -(- 13 090 „

О =

—

= 2,473.

825

Далее вычисляем уклонения (см. табл. 77) V, = 0,168*1 + Ь —

— У1 и осуществляем контроль на основании (3.15) или в подробной

записи [хь] = —0,18 « 0, [»] = —0,03 « 0.

Для оценки точности вычисляем

Н омера

•

наблю

1 "1

дений

1 "1

1 2,8

—0,16

2.7

+0,11

3 2,9

+0,08

3,3 —0,16

3,2

+0,11

6 6 3,4

+0,08

3,6 +0,05

3,9

—0,08

9 9

4,0

—0,02

10 10 4,2

—0,04

55 34,0 —0,03

|и

1 = 0,9991;

т —

/М99Г

— 2

Согласно формуле (3.47) т

= тУОп, т

= тУ 0

гг

п 10

где

[х

] п— [*]

О I*

>С22 —

825

385

Поэтому

[х

] п — [х

]

825

= 0,0121;

= 0,467.

= 0,11 |/0,0121 =0,012; = 0,11 /о,467 = 0,068.

Можно показать, что, когда функциональная зависимость имеет

вид у = ах + Ь, задача нахождения параметров а и Ь математически

тождественна задаче построения уравнения регрессии, однако по су-

ществу отличается от нее, так как наличие функциональной связи

предполагает, что коэффициент корреляции л=±1. Так, применяя

метод наименьших квадратов к задаче 2.41, получим то же уравнение

регрессии у = 0,63л; + 0,71, но говорить о функциональной связи

между у и х не приходится (это видно уже по расположению точек на

графике рис. 33).

Аналогично решается задача и для подбора параметров полиномов

более высокого порядка в общем виде

3.42. Составить коэффициенты нормальных уравнений для определения

коэффициентов полинома у = ах'

4- Ьх + с.

197

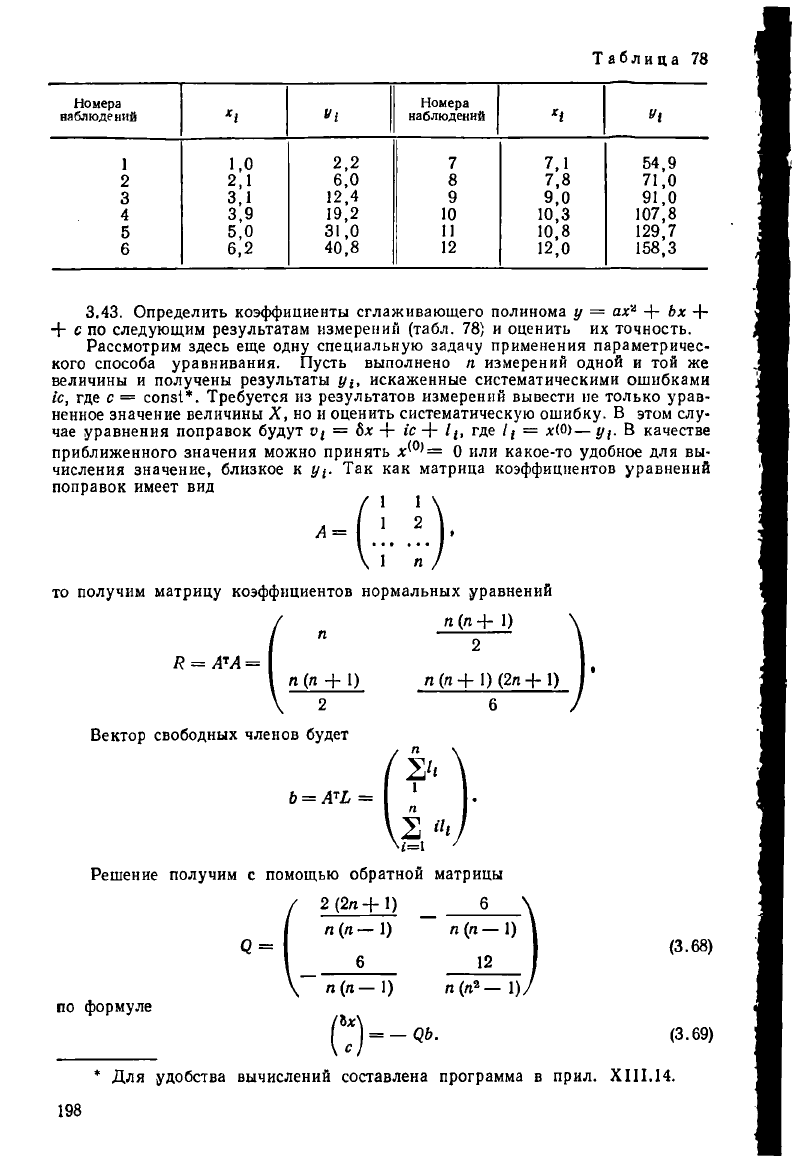
Таблица 81 Таблица 83

Номера

наблюдений

УI

Номера

наблюдений

УI

1,0

2,1

3.1

3,9

5,0

6.2

2,2

6,0

12,4

19,2

31,0

40,8

7,1

7,8

9,0

10,3

10,8

12,0

3.43. Определить коэффициенты сглаживающего полинома у = ах* + Ьх +

+ с по следующим результатам измерений (табл. 78) и оценить их точность.

Рассмотрим здесь еще одну специальную задачу применения параметричес-

кого способа уравнивания. Пусть выполнено п измерений одной и той же

величины и получены результаты искаженные систематическими ошибками

1С,

где с = сопз1*. Требуется из результатов измерений вывести не только урав-

ненное значение величины X, но и оценить систематическую ошибку. В этом слу-

чае уравнения поправок будут = Ьх + 1с + где 1

(

= х(0)— у,. В качестве

приближенного значения можно принять *'

= 0 или какое-то удобное для вы-

числения значение, близкое к у

. Так как матрица коэффициентов уравнений

поправок имеет вид

(

1 1

\ 1 п

то получим матрицу коэффициентов нормальных уравнений

я(я + 1)

Я = ЛМ =

и (я + 1) п(п+ 1) (2я+ 1)

2 6

Вектор свободных членов будет

= ХЧ =

2 «I

4=1

Решение получим с помощью обратной матрицы

2 (2я + 1) 6

п(п— 1) я (л — 1)

(3=| | (3.68)

6 12

по формуле

л (л — 1) л (я

— 1)/

(3.69)

* Для удобства вычислений составлена программа в прил. XIII.14.

198

Таблица 81 Таблица 83

Значения у.

Номера

приемов

Значения у^

Номера

приемов

Значения у.

90°15'27,5"

29,7

30,9

34,6

34,1

31,3

33,5

90°15'37,3"

33.6

31.7

33.2

37,9

34,9

35.3

27,2

90" 15'35,5"

38.8

33.3

32,1

38,7

39,1

39.4

39.9

Средние квадратические ошибки

т,

где

_ /~2 (2п + 1) .. Г 12

= т

У Т^ГТГ

= Т

У ^ГГЦ'

У п—к У п — 2

(3.70)

Рассмотрим следующий пример. В табл. 79 даны 24 измерения зенитного

расстояния на одном из пунктов триангуляции*.

Предполагая, что измерения выполнялись равномерно во времени и влия-

ние систематической ошибки пропорционально времени, получить наиболее на-

дежное значение измеренного угла, оценку систематической ошибки с и оценить

точность измерений и результатов.

Решение. В качестве приближенного значения примем величину

.(0)

90° 15'20". Тогда найдем

2/, =-339,2; 2 «, = —4642,4.

1=1

Матрица (3.68)

/ 0,177536 —0,010870\

(—0,010870 0,000870/ '

оэтому решение (3.69)

= *

(0>

+ Ьх = 90°

15'

29,76".

По смыслу задачи это будет наиболее надежное значение угла, отнесенного

к начальному моменту измерений.

Для величины 2

?' опуская здесь вычисления, согласно формуле (3.70)

найдем

1=1

* Смирнов Н. В., Белугин Д. А. Теория вероятностей и математическая ста-

тистика в приложении к геодезии. М., Недра, 1969.

199

Поэтому точность измерений характеризуется средней квадратической ошибкой

Л73Х „ „,„

= У "Й-=

а ошибки

= 2,81 /ОТШ" = 1,18"; «,. = 2,81 /0,00087 =0,08".

Заметим, что если решать эту задачу, не предполагая наличия систематических

ошибок, то получим

* = 90°15'34,3"

и т «= 3,72", не соответствующую точности измерений данным теодолитом.

3.44. Доказать, что если в каждом измерении одной и той же величины сис-

тематическая ошибка постоянна, то ее невозможно выявить рассмотренным спо-

собом, а величина т не будет искажена систематическим влиянием.

3.45. Составить матрицу коэффициентов нормальных уравнений, если сис-

тематическая ошибка действует по законам: 1) (/ + Ь)с, 2) Рс, 3) ш

с, приняв

п » 5.

3.46. С помощью таблицы случайных чисел (прил. XI) смоделировать ошиб-

ки п «= 10 измерений со стандартом а = 2 и с = 1, если систематические ошиб-

ки действуют по закону {с, где I — номер измерения. Получить оценку для сис-

тематической ошибки, оценить точность ее определения и точность измерений.

3.47. Сделать то же самое, если закон действия систематических ошибок

ф(с) = С81па

, где Щ = а^ + I

§ 34. УРАВНИВАНИЕ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

ПАРАМЕТРИЧЕСКИМ СПОСОБОМ

Уравнивание неравноточных измерений выполняется под услови-

ем [рцо\=У

РУ= пил, где р

— веса измерений, а Р — диаго-

нальная матрица,

Вопрос установления весов р

был нами рассмотрен в § 24.

Исходная система связи и уравнения поправок составляются так

же, как и в случае равноточных измерений, но в отличие от него сис-

тема нормальных уравнений имеет вид

[раа] + \раЬ\ Ьх

+ ... + \ра§\ Ьх

+ [ра1\ = 0,

\раЬ\ Ьх

+ [рЬЬ] Ьх

+ ... + \рЬ§\ Ьх

+ \рЫ\ = 0,

\ра

\ Ьх, + [рЬ§\ Ьх

+ ... + \р

\ Ъ

+ \РёП = 0,

где алгоритмы

[раа] = р

а,а

+ р

а.

+ •••' + р„а

[раЬ] = даД + р

а.

+ • • • + р

\ра1\ = р,^/, + р

+ • • • + р

200.

1Р§1\ = РхёхК + РгёА +

Рпёпк-

В матричной форме уравнения (3.71) можно записать в виде

КАх+Ь = 0,> (3.72)

где

Я = А

РА, (3.73)

Ь = А

РЬ. (3.74)

Процесс вычислений при уравнивании неравноточных измерений,

следовательно, отличается от уже рассмотренного случая лишь схе-

мой составления нормальных уравнений. При этом можно поступить

двояко; 1) привести неравноточные измерения к равноточным путем

умножения г-го уравнения поправок на величину У~р7, 2) нормаль-

ные уравнения составлять непосредственно по формулам (3.13) и (3.14).

В первой схеме (А) будем иметь систему уравнений поправок

V, = 0,8*! + + • • • + ~ё$Х

+ Т^

= а

Ьх, + Ьфх

+ • • • +

V„ = а

Ьх, + Ь

Ьх

Н 1- д

Ьх

+ 1

где

VI = V, УТГ;

щ = а

-- ь

У~Р7\ ... \ё1 = ё1 У~Р\\ 7 =

и систему нормальных уравнений

[аа] Ь

Х{

+ [а Ь] Ьх

+ • • • + [а ё] Ьх

+ Га Л = О,

[а &]8л:! + [ЬЬ]Ьх

+ ••• + =0,

[а ^ Ьх, + [Ь ^] Ьх

+ • • • + Ъх

+ 7] = О,

совпадающую с (3.72). Ясно, также, что [ргю] = [и, о]. Схема состав-

ления системы нормальных уравнений будет состоять из следующих

двух таблиц (табл. 80, 81). Для простоты принято к = 3.

Во второй схеме (В), которую применяют чаще, приходится состав-

лять следующие таблицы (табл. 82 и 83).

Таблица 80

Номера

измерений

ут,

а, ~с

{

~> |

а, Ь

{

°2 с* к

«1

Ур

1 Ь

а, Ь

е.,

п 'п

«л УТп

п «г. | Оп

201.

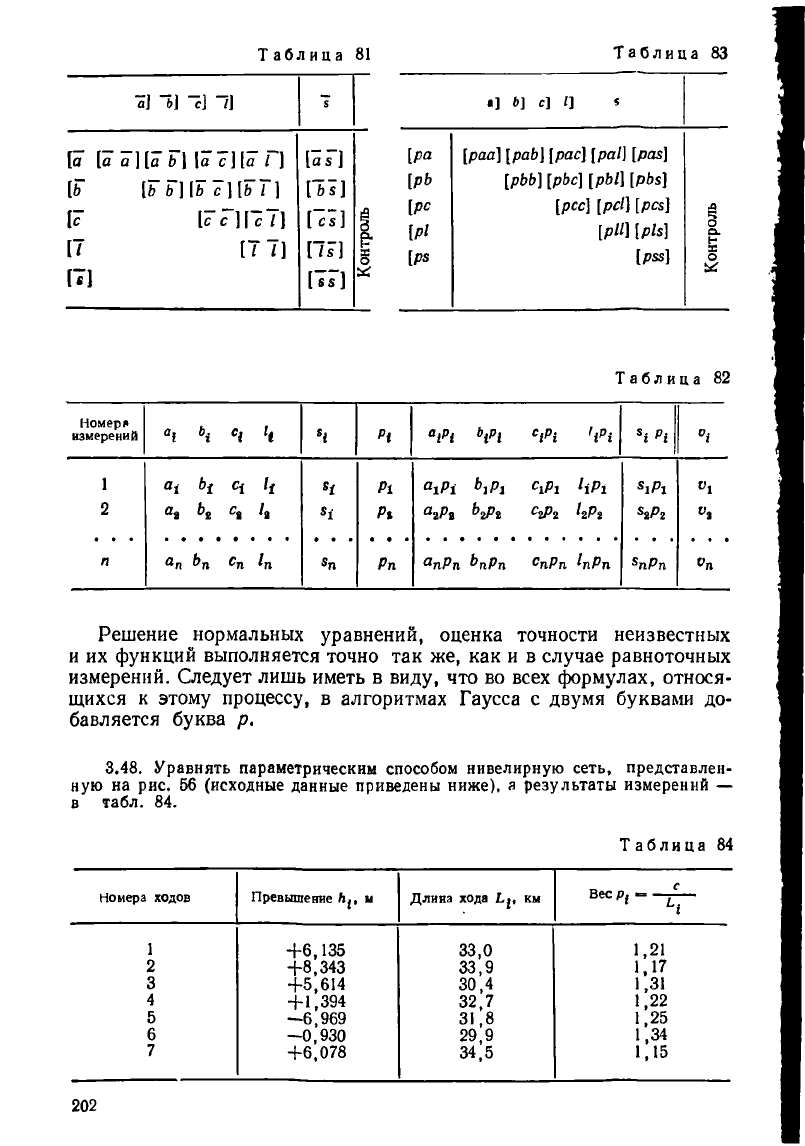
Таблица 81

а] (.] с] /]

[а [а

а][а Ь \ \а~с\\а Г] [а Г]

[ь [ь ь]\ь7][ьТ]

Гь*]

1с

[ГГ] [77]

Гс~з]

[7 7]

[7Г]

[71 [ТГ]

Таблица 83

•] Ь] с] /] «

[ра

[раа] [раЬ] [рас]

[ра1]

[раз]

[рЬ

[рЬЬ] [рЬс]

[рЫ] [рЬ$]

[рс

[рсс]

[рс1] [РС5]

[Р1

1РП [Р&]

а.

[/»

[ри]

Таблица 82

Номер»

измерений

{

Р,

(

р. 1

{Р1

Ьх Ч к Р1

Ь]Р1

С1Р1 '1Р1

ЧР1

«1

а»

Ьг

«1 Р»

гРг

Ь&г

с-гРг 1

ЧРг

Ьп Сп

1п «П

Рп

пРп ЬпРп

СпРп

пРп

&пРп Рп

Решение нормальных уравнений, оценка точности неизвестных

и их функций выполняется точно так же, как и в случае равноточных

измерений. Следует лишь иметь в виду, что во всех формулах, относя-

щихся к этому процессу, в алгоритмах Гаусса с двумя буквами до-

бавляется буква р.

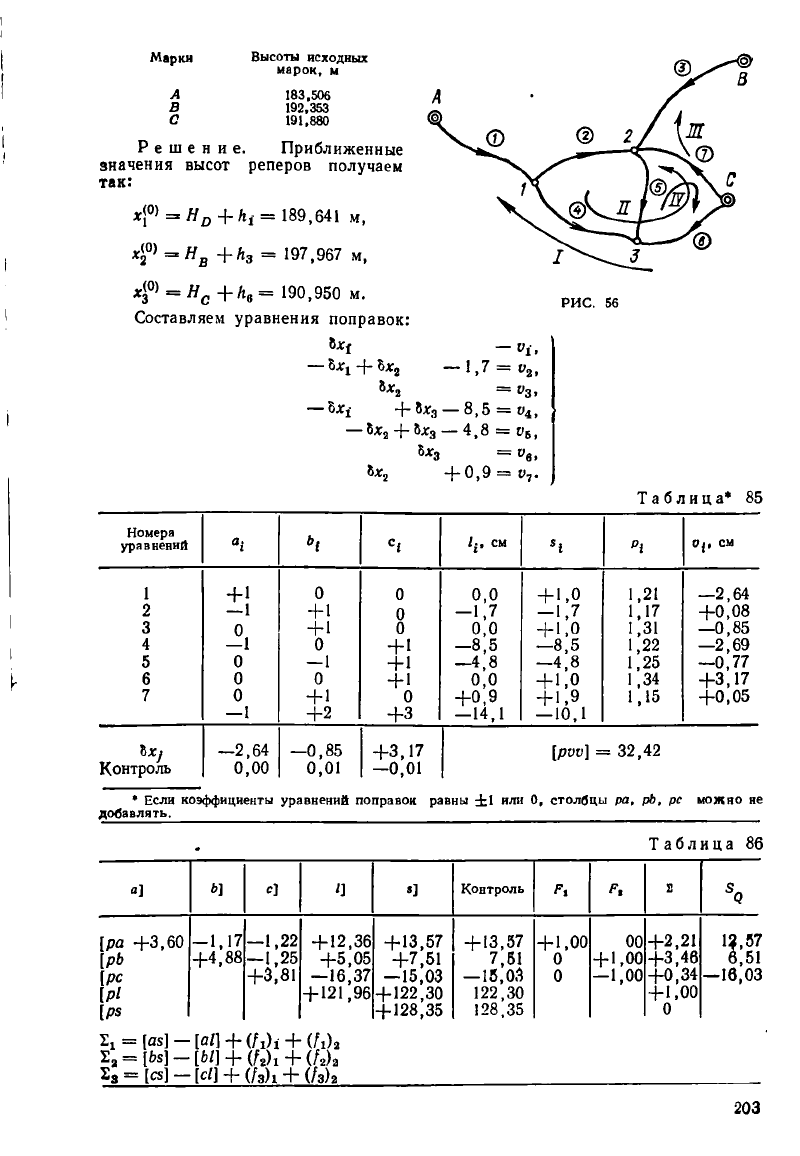
3.48. Уравнять параметрическим способом нивелирную сеть, представлен-

ную на рис. 56 (исходные данные приведены ниже), а результаты измерений —

в табл. 84.

Таблица 84

Номера ходов

Превышение Н

{

, м

Длина хода км

Вес

4-6,135

4-8,343

4-5,614

4-1,394

—6,969

—0,930

4-6,078

33,0

33,9

30.4

32.7

31.8

29.9

34.5

1,21

1,17

1,31

1,22

1,25

1,34

1.15

202

Марки

Высоты исходных

марок, м

183,506

192,353

191,880

Решение. Приближенные

значения высот реперов получаем

так:

• = 189,641 М,

•Н

+ й

= 197,967 м,

{

°> = Я

+Й

= 190,950 м.

Составляем уравнения поправок:

а*

РИС. 56

-В*,

—

<>1.

— 1,7 =

= с

+ 8*з — 8,5 = 04,

—

8*2

8*3

— 4,8 = у

Ьх,

+ 0,9 = о,.

Таблица* 85

Номера

1-, см

уравнений

1-, см

С|, см

0,0

+ 1,0 1,21

—2,64

— 1

-1,7 -1,7

1,17 +0,08

0,0

+ 1,0 1,31 —0,85

4 —1

-8,5 —8,5 1,22

—2,69

0 —1

-4.8

-4,8

1,25

—0,77

0 0

0,0

+ 1,0

1,34 +3,17

7 0

0 +0,9

+1,9

1,15

+0,05

—1

+3 -14,1

—10,1

1,15

]

—2,64

—0,85 +3,17

[РМ = = 32,42

Контроль

0,00 0,01

—0,01

[РМ =

* Если коэффициенты уравнений поправок равны ±1 или 0, столбцы ра, рЬ, рс можно не

добавлять.

Таблица 86

о]

ь] с]

Контроль

Г,

Р.

[ра +3,60

[рЬ

[рс

№

[р$

-1,17

+4,88

—1,22

-1,25

+3,81

+ 12,36

+5,05

—16,37

+121,96

+13,57

+7,51

-15,03

+122,30

+128,35

+ 13,57

—15,03

122,30

128,35

+1,00

+ 1,00

—1,00

+2,21

+3,46

+0,34

+1,00

12,57

6,51

—16,03

1!= [08] -И+ (/!>* + (/,),

[Ьв]

- [6/] + (/

)

+ (/

)

Ез - [я] -

[с1]

+ Ц

)

+ (/3)2

203.