Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Доверительный интервал для истинного значения Р любой функ»

ции Р уравненных измерений строят в виде

Р — (

-т~<Г<Р + (ж~, (3.78)

р р р р

где коэффициент Iр выбирают из таблиц распределения Стьюдента

по доверительной вероятности р и числу степеней свободы г = п—к,

а средняя квадратическая ошибка

= ц 1/Т7РГ.

Р ' Г

В частном случае для истинного значения X) уравненного пара*

метрическим способом неизвестного будем иметь интервал

* — <

} < * + V

* /'

где т

Х/

= ц

Так, в задаче 3.48 для уравненных отметок узловых точек ниве-

лирной сети получим доверительные интервалы, построенные с веро-

ятностью 0,95 (коэффициент Ц при г = 4 равен 3,2)

189,614 — 3,2 • 1,75- 10"

<Х

< 189,614 + 3,2 • 1,75- 10"

;

197,958 — 3,2-1,48 • 10"

< < 197,958 + 3,2 . 1,75 . 10"

;

190,981 —3,2 . 1,70 < Х

< 190,981 + 3,2 • 1,70 • 10"

189,558 <*!< 189,670;

197,911 <Х

< 198,005;

190,927 <Х

< 191,035.

Для истинных значений уравненных превышений У

{

и Уъ получе-

ны доверительные интервалы

6,053 < У

< 6,165; — 7,032 < У

< — 6,922.

Иногда результат уравнивания записывают в виде х

± т

Х)

, что

при большом г соответствует доверительному интервалу при р « 0,7.

Доверительный интервал для с. к. о. единицы веса строят в виде

ЪИ < ст

< (3.79)

причем коэффициенты

Ь = |/(/г-/г)/х? - Т2 = У(п-к)/х1

выбираются из таблиц распределения х

, как описано в § 19, но по

числу степеней свободы г = п—к. Так, для с. к. о, о

при р = 0,90

= 4 будем иметь х? = 9,5, хз = °.

доверительный интер-

вал для с

в задаче 3.48

* По таблицам прил. VIII сразу находим у

(

= 0,649 и Уа = 2,37.

214.

/4/9,5 2,85 < о

< V 4/0,71 2,85; 1,8 см < <т

< 8 см.

Для с. к. о. функции о~ доверительный интервал будет

а для а

< о-. <

11™,, < % < .

(3.80)

Например, для ст*. в этой же задаче будем иметь доверительный ин-

тервал 1,1 см <0*, < 4,2 см.

Иногда вместо построения доверительного интервала для ст

вы-

числяют «ошибку ошибки» т^ « 1иУ~2г и пишут интервал в виде

' (при достаточно большом г) ц± т^ , а также т

+ т

, где

1 XI

т„

3.55. Построить доверительные интервалы для истинных значений урав-

ненных углов в задаче 3.50 и для их средних квадратических отклонений, приняв

Р = 0,90; Р = 0,95; Р = 0,99.

3.56. Построить доверительные интервалы для истинных координат пунк-

тов О и С, для средних квадратических отклонений о

хо

, а

у0

и а

Хс

, а

ус

, для сред-

них квадратических отклонений функций в задачах 3.37, 3.38, 3.50 (доверитель,

ная вероятность Р = 0,95).

§ 36. РЕШЕНИЕ НОРМАЛЬНЫХ УРАВНЕНИЙ ПО МЕТОДУ КВАДРАТНЫХ

КОРНЕЙ. ОБ ОШИБКАХ ВЫЧИСЛЕНИЙ

Как мы уже знаем (см. § 29), метод Гаусса решения системы

нормальных уравнений

ЯД+ 6 = 0 (3.81)

сводится к представлению матрицы 7? в виде произведения Я — Т{Гъ

(см. стр. 159).

При этом получаем две системы уравнений

= — Ь; Т

А = у,

где у — преобразованный в схеме Гаусса вектор Ь. Искомый вектор

ДТ~2 у получается в схеме Гаусса по приведенным ранее формулам.

Метод квадратных корней заключается в представлении матрицы в

виде произведения Я = Т

Т, где матрица

Т =

У\аа)

У[ЬЪЛ] •

У[аа\

[ЬД-П

[ЬЬ

• 1]

У88-&-1)

215.

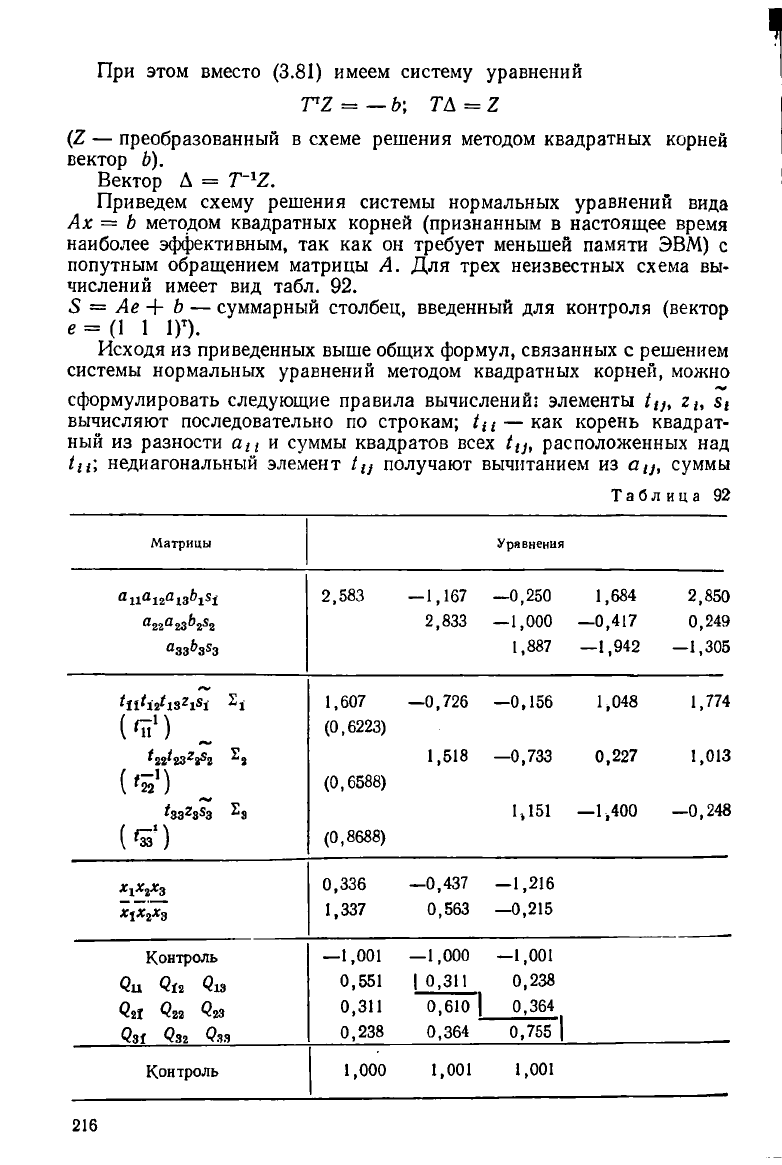
При этом вместо (3.81) имеем систему уравнений

гг = —ь-, та =2

(2 — преобразованный в схеме решения методом квадратных корней

вектор Ь).

Вектор Д = Т'

Приведем схему решения системы нормальных уравнений вида

Ах = Ь методом квадратных корней (признанным в настоящее время

наиболее эффективным, так как он требует меньшей памяти ЭВМ) с

попутным обращением матрицы А. Для трех неизвестных схема вы-

числений имеет вид табл. 92.

5 = Ае + Ь — суммарный столбец, введенный для контроля (вектор

е=(1 1 1)

Исходя из приведенных выше общих формул, связанных с решением

системы нормальных уравнений методом квадратных корней, можно

сформулировать следующие правила вычислений; элементы 1ц, г

1у

(

вычисляют последовательно по строкам; I

— как корень квадрат-

ный из разности а и и суммы квадратов всех (ц, расположенных над

(и; недиагональный элемент 1ц получают вычитанием из а

, суммы

Таблица 92

Матрицы

Уравнения

1«1

2,583 -1,167 —0,250

1,684

2,850

2,833 —1,000

—0,417

0,249

азз

з*з

1,887

—1,942

—1,305

1,607

—0,726 —0,156

1,048

1,774

(и

)

(0,6223)

1,518

—0,733

0,227 1,013

(0,6588)

'33

1,151

—1,400

-0,248

(0,8688)

0,336

—0,437

— 1,216

1,337

0,563 —0,215

Контроль

—1,001

—1,000

—1,001

Си Си

0,551

1 0,311

0,238

а* ^22 Саз

0,311 0,610 |

0,364

С>31 Ряя

0,238

0,364

0,755 |

Контроль

1,000

1,001

216.

произведений элементов I, взятых из столбцов г и /, и умножением

полученной разности на 1ц\ аналогично вычисляют и элементы г

{

***

И 5/.

После вычисления всей строки производят контроль

2 п, + г, = 2,

(расхождения между 2

и х

(

) допускаются в пределах нескольких

единиц последнего удерживаемого знака).

Неизвестные х

{

определяют по формулам

= г

к*кк

1 ~ —

*11

^ '

•

Точно так же по столбцу 5 по мере получения х

вычисляют ве-

личины XI и осуществляют контроль XI—XI = 1.

Отметим, что при числе уравнений к<. 10 в элементах 1ц удер-

живают на 1—2 знака после запятой больше, чем их имеют элементы

ац, при 10 < к < 30 — на 3—4 знака больше.

Приведенная схема вычислений удобна и для обращения матрицы

А. В самом деле, если решение системы уравнений Ах = Ь сводится

к последовательному решению двух систем

Тг = Ь и Тх = 2,

то процесс обращения матрицы А, заключающийся в решении систем

АС1) = Е

}

(/ = 1, 2, ..., к), где и Е

{

— соответственно ;'-е столбцы

матриц А и Е, может быть сведен к решению двух систем

Т% = Е]\ (3.82)

ТО, = 1

}

. (3.83)

Из системы (3.82) следует, что вектор

Учитывая правило обращения треугольной матрицы и введя мат-

рицу 2, столбцами которой служат векторы напишем

С" \

2(Г)"

Е = (Г

= ^ |.

? С

Здесь знаком вопроса обозначены неизвестные недиагональные

элементы матрицы (Г

. Из системы (3.83) следует, что столбцы

матрицы ф могут быть получены в схеме решения точно так же, как

217.

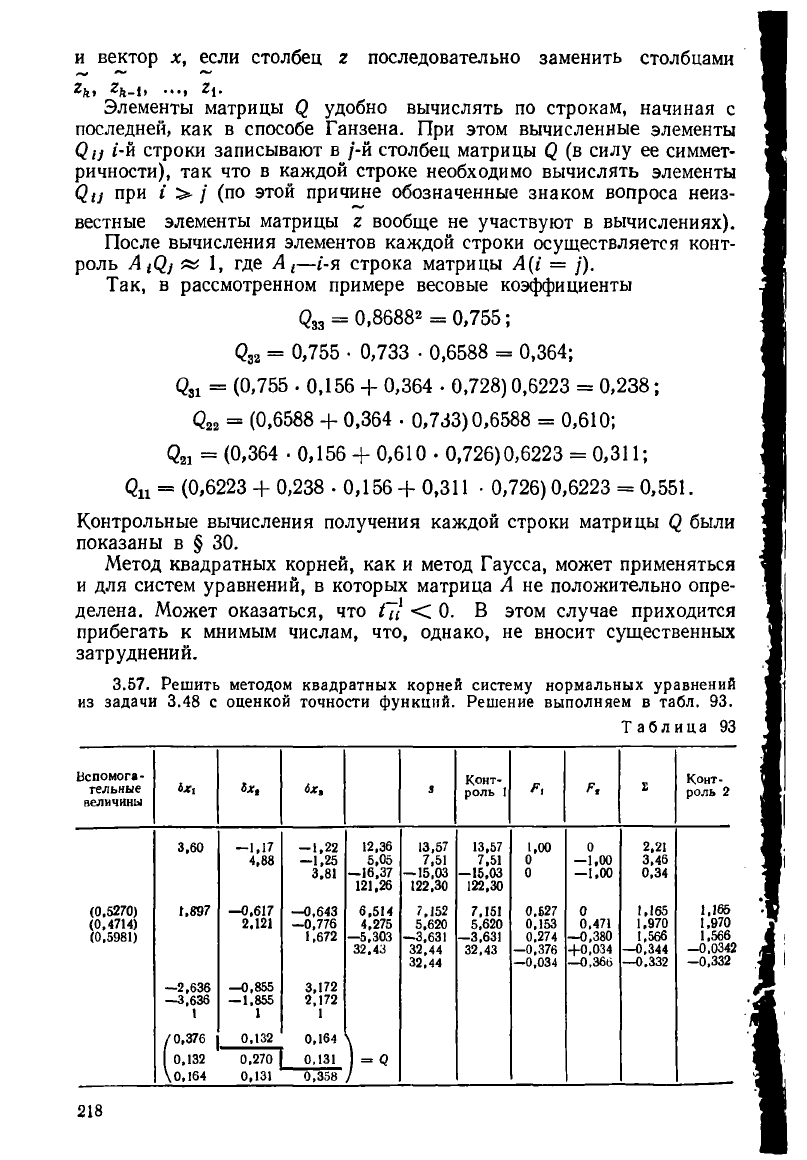
и вектор х, если столбец г последовательно заменить столбцами

й>

к-1> •••>

Элементы матрицы С} удобно вычислять по строкам, начиная с

последней, как в способе Ганзена. При этом вычисленные элементы

1-й строки записывают в /-й столбец матрицы ф (в силу ее симмет-

ричности), так что в каждой строке необходимо вычислять элементы

С}

{

] при I > / (по этой причине обозначенные знаком вопроса неиз-

вестные элементы матрицы г вообще не участвуют в вычислениях).

После вычисления элементов каждой строки осуществляется конт-

роль « 1, где А

—1-я строка матрицы АЦ = /).

Так, в рассмотренном примере весовые коэффициенты

= 0.8688

= 0,755;

<Э

= 0,755 • 0,733 • 0,6588 = 0,364;

<Э

= (0,755 • 0,156 + 0,364 • 0,728) 0,6223 = 0,238;

С}

= (0,6588 + 0,364 • 0,733)0,6588 = 0,610;

= (0,364 • 0,156 + 0,610 • 0,726)0,6223 = 0,311;

= (0,6223 + 0,238 • 0,156 + 0,311 • 0,726)0,6223 = 0,551.

Контрольные вычисления получения каждой строки матрицы <2 были

показаны в § 30.

Метод квадратных корней, как и метод Гаусса, может применяться

и для систем уравнений, в которых матрица А не положительно опре-

делена. Может оказаться, что <1 0. В этом случае приходится

прибегать к мнимым числам, что, однако, не вносит существенных

затруднений.

3.57. Решить методом квадратных корней систему нормальных уравнений

из задачи 3.48 с оценкой точности функций. Решение выполняем в табл. 93.

Таблица 93

Вспомога-

тельные

величины

Ьх,

6х,

Конт-

роль I

Л г,

Конт-

роль 2

3,60

-1,17

4,88

— 1,22

-1,25

3,81

12,36

5,05

—16,37

121,26

13,57

7,51

— 15,03

122,30

13,57

7,51

-15,03

122,30

1,00

—1,00

—1.00

2,21

3,46

0,34

(0,5270)

(0,4714)

(0,5981)

1,897

—2,636

—3,636

/0,376

—0,617

2,121

-0,855

— 1.855

0,132

—0,643

-0,776

1,672

3,172

2,172

0,164

6,514

4,275

—5,303

32,43

7,152

5,620

—3,631

32,44

7,151

5,620

-3,631

32,43

0,627

0,153

0,274

—0,376

—0,034

0,471

—0,380

+0,034

—0,366

1,165

1,970

1,566

—0,344

—0.332

1,165

1,970

1,566

—0,0342

-0,332

0,132

0,270 0,131

1-е

\0,164 0,131

0,358

218.

Заметам, что алгоритмы [рИ.к], [рЫ.к] и [рк.й] и величины -3— и 77—вычисля-

Р,

ют аналогично тому, как это делается в схеме Гаусса.

3.58. Решить методом квадратных корней системы нормальных уравнений

из задачи 3.18.

3.59. Решить методом квадратных корней систему нормальных уравнений,

возникающую в задаче 3.17.

При решении систем нормальных уравнений неизбежны погрешности вы-

числений двух видов.

1. Погрешности из-за неизбежных округлений при вычислениях, поэтому

вместо точных неизвестных ху мы получаем X/ =

] -Ь 6у. Подставив

ис-

ходную систему уравнений, вместо свободных членов получим свободные чле-

ны ЬI = Ь] + ЬЬ].

Если невязки бЬ] превышают 1—2 единицы последних цифр свободных чле-

нов, то следует уточнить решение, приписав к схеме Гаусса дополнительно стол-

бец 66. При этом точно так же, как описано выше, будут найдены поправки

Указанный процесс можно повторять неоднократно до тех пор, пока поправка-

ми, найденными на р-и шаге, можно будет пренебречь. Обычно при небольшом

числе уравнений необходимость в указанных действиях отпадает.

2. Погрешности, возникающие из-за ошибок в коэффициентах и свободных

членах исходной системы, не могут быть устранены. Однако можно вычислить

погрешность получения неизвестных *у. Допустим, что известны максимальные

погрешности коэффициентов и свободных членов, которые мы обозначим через

Да

Аь> тогда можно показать, что максимальное искажение свободных членов

(максимальная «невязка») составит одинаковую в каждом уравнении величину

й = Д

21*/1 + ^Ь- И тогда, приписав к системе уравнений столбец Д, состоя-

/=1

щий из единиц, и рассматривая его как столбец свободных членов Ь, получим

неизвестные Д*!, Д*

, ..., Д*&.

Эти величины вычисляются так же, как и 6*у, но так как знаки погрешнос-

тей Д

и Д;, неизвестны, то, рассчитывая на самый неблагоприятный случай,

мы должны оперировать только с модулями всех участвующих в вычислениях

чисел. Таким образом (при к = 3),

Т"

— _

2.1 [рЬс. 1] _ .

~ ~№Ь1Г 1РЬЬАГ

[раа] [раа] [раа\

Окончательно получаем неустранимые погрешности вычисления каждого

неизвестного по формуле Д*у =• ЛД*у.

На самом деле погрешности, конечно, значительно меньше.

Ниже приводится пример решения системы трех уравнений [8]:

4,15*] + 1,9

*„ + 1,95*з — 3,20 = 0;

1,98*, + 3,02л:

+ 0,99*з — 2,60 = 0;

1,95*! + 0,99*

+ 3,01*з — 2,10 = 0

при Да = Д& = 0,005.

Решение по схеме Гаусса дано в табл. 94.

3.60. Самостоятельно выполнить решение по методу квадратных корней и

сравнить погрешности вычислений в каждом методе.

219.

Таблица 81 Таблица 83

Контроль

4,15

—1,000

1,98

—0,477

1,95

—0,470

—3,20

0,771

4,88

— 1,776

—1,776 0,241

2,08

—1,000

0,06

—0,029

-1,07

0,514

1,06

—0,510

1,07

—0,515

1,48

0,712

2,09

—1,000

—0,56

0,268

1,53

—0,732

1,53

—0,732

1,51

0,723

X) 0,404

7] —0,599

1,003

0,506

—0,489

0,995

0,268

—0,732

1,000

4= Аа + =

/=1

= 0,005 • 1,2 +0,005 = 0,011

~Кх] 0,93

Ах) 0,010

0,73

0,008

0,72

0,008

4= Аа + =

/=1

= 0,005 • 1,2 +0,005 = 0,011

§ 37. СПОСОБЫ ПРИБЛИЖЕНИЙ РЕШЕНИЯ НОРМАЛЬНЫХ УРАВНЕНИИ

При решении большого числа нормальных уравнений часто при-

меняют не прямые способы, к которым принадлежат рассмотренные

ранее способы Гаусса и квадратных корней, а так называемые способы

приближений. Если в прямых способах решение получают путем вы-

полнения конечного, заранее известного числа арифметических опе-

раций, то способы приближений основаны на постепенном уточнении

неизвестных, выполняемом до тех пор, пока максимальная разность

—х

{т

будет меньше наперед заданного положительного

числа е, определяемого необходимой точностью вычислений. Число

приближений р при этом заранее указать невозможно. Вычисление

неизвестных х

(

™

}

в каждом т-м приближении требует значительно

меньшего объема вычислений, чем получение неизвестных в прямых

методах. Эффективность способов итераций, следовательно, целиком

определяется количеством приближений, которое зависит от скорости

сходимости процесса. Объем вычислений в прямых методах возрастает

примерно пропорционально кубу числа уравнений, поэтому способы

итераций для решения больших систем уравнений часто оказываются

более эффективными.

Прежде чем начать вычисления, систему уравнений Ах = Ь не-

обходимо привести к виду, удобному для итераций,

* = а* + р. (3.84)

Пусть дана система нормальных уравнений

220

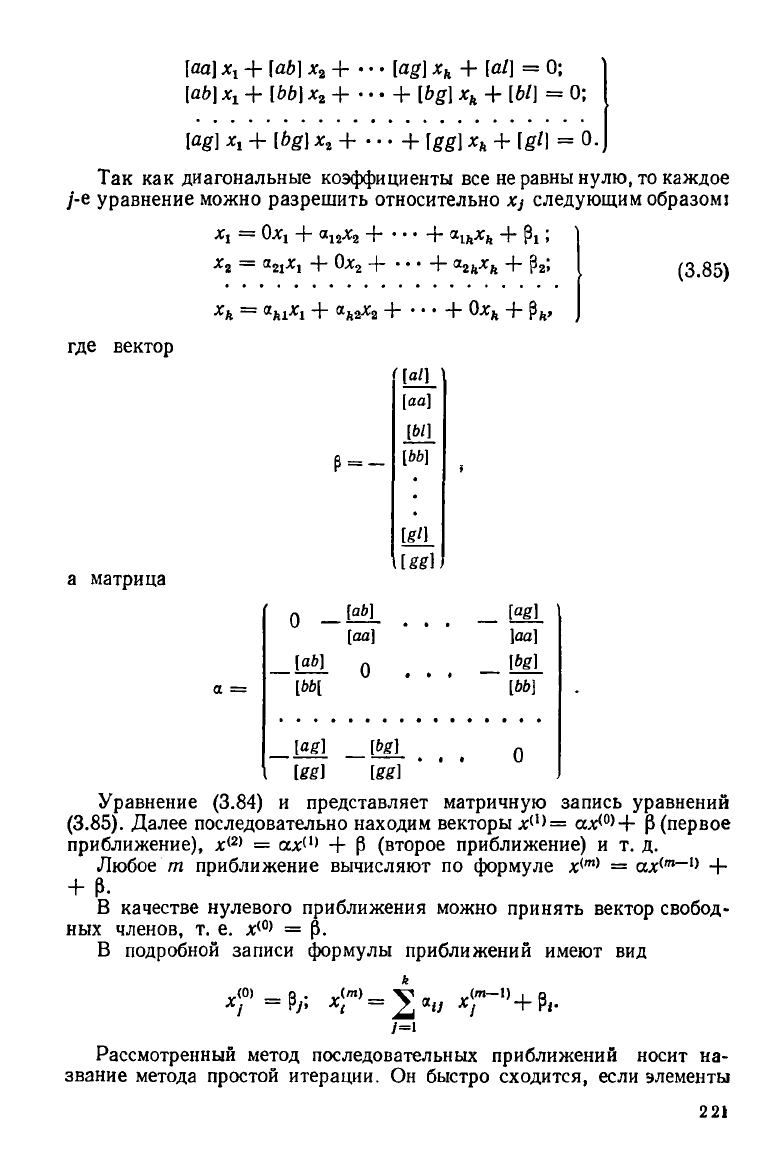
[aa] х

+ [аЬ] х

-\ [а^] х

+ [а/] = 0;

[ab] х

+ [ЬЬ] х

+ • • • + [Ь§] х

+ [Ы] = 0;

[а^] х

+ [М + • • • + [

ёё

] + = 0.

Так как диагональные коэффициенты все не равны нулю, то каждое

у'-е уравнение можно разрешить относительно X) следующим образом:

Л:, =

Олг!

+ а

+ Ь <г

1к

+ ?!;

= + 0х

+ • • • +

2к

$2>

где вектор

*к = «йЛ +

кЛ

-1

Ь + К>

[а/1

(3.85)

а матрица

[аа]

[Ы]

[ЬЬ]

[88]

а =

0 —

[аЬ]

[°8]

0 —

[<ю]

]аа]

[аЬ]

0 .

№

[ЬЬ[

0 .

[ЬЬ]

. . 0

[й?] [88]

Уравнение (3.84) и представляет матричную запись уравнений

(3.85). Далее последовательно находим векторы я

(1)

= ах

<0)

+ р (первое

приближение), х

{2)

= ах

(1)

+ Р (второе приближение) и т. д.

Любое т приближение вычисляют по формуле х

(т)

= ах

(т

+ Р-

В качестве нулевого приближения можно принять вектор свобод-

ных членов, т. е. дс

(0)

= р.

В подробной записи формулы приближений имеют вид

*Г= РУ; *Г=2> *Г

_1)

/=1

Рассмотренный метод последовательных приближений носит на-

звание метода простой итерации. Он быстро сходится, если элементы

221.

матрицы а малы по абсолютной величине. Достаточные условия схо-

димости процесса следующие:

1) М-тах^КК!.

/=1

или 2) || а ||

= тах ^ | а

| < 1

1 = 1

/ к к

или з) и а//, = -./ 2

1=1

/='

<1.

Величины ||а||

||а||

, называемые соответственно первой и вто-

рой нормой матрицы а, представляют максимальную сумму модулей

элементов матрицы а по строкам или столбцам. Третья норма ||а||

есть сумма квадратов всех ее элементов. Можно также доказать, что

сходимость имеет место, если диагональные элементы матрицы А си-

стемы превышают сумму модулей недиагональных элементов для каж-

дой строки или для каждого столбца. В качестве примера решим си-

стему нормальных уравнений

2,583 —1,167 —0,250\ / х,

—1,167 2,833 —1,000 |[ х

| +

—0,250 —1,000 1,887,

'—1,684

+0,417 1 = 0. (3.86)

,+ 1.942

Легко проверить, что процесс будет сходиться, так как 2,583 > 1,417;

2,833 > 2,167; 1,887 > 1,250.

Вычисления располагаем в табл. 95.

Таблица 95

"и '13 Ь

„(3)

0,412

0,132

0,452

0,530

0,097

0,353

0,652

-0,147

—0,029

0,5

—0,2

-1,0

0,46

—0,29

-1,12

0,41

—0,38

' -1,18

Продолжение табл. 95

(4>

,С5)

„(6)

.(8)

„(Ю)

0,37

—0,39

—1,19

0,36

—0,41

—1,20

0,35

—0,42

—1,20

0,34

—0,43

-1,21

0,340

—0,434

— 1,212

0,338

—0,435

—1,215

0,338

—0,437

-1,215

0,337

—0,437

—1,216

222.

Так как шах 1л:'/

— лг

(

| = 0,001, то вычисления заканчиваем.

Значения неизвестных получились такими же, как и при решении

нормальных уравнений по схеме Гаусса или методу квадратных кор-

ней (см. примеры в § 29, 36).

Отметим, что так как окончательный результат не зависит от на-

чального приближения, то точность вычислений целесообразно уве-

личивать по мере улучшения сходимости.

Видоизменением метода простой итерации является метод

3 е й д е л я, который для системы нормальных уравнений всегда

сходится. Отличием этого метода является то, что при вычислении

(

У используются значения (/=1,2, ..., /—1), уже получен-

ные в этом же приближении. Формулы для вычислений имеют вид

<т) _ -V _ „(т-1) , о .

\ —

/=2

{

т)

х\

т)

*<"-»+ р

;

/=2

/=1 /—1

(т) _ ^ (т) , (т—1) I о

к ~ 2л

к1

+ кк

/=1

Например, для к = 3

*Г' = «11 + ^Г"

' + «13 Р»

П)

= «

Х^ + а

+ «

з К

Лт) _ _ „(л») I _ (т—I) , (т—1) , о

31 + «32 Х

+ «33

з + Рз-

В табл. 96 приведено решение системы (3.86) но методу Зейделя.

т аблица 96

'И

•12

"гз

0,412

0,132

0,452

0,530

0,097

0,353

0,652

—0,147

—1,029

0,5

—0,3

-1,1

0,41

-0,31

— 1,14

223.