Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

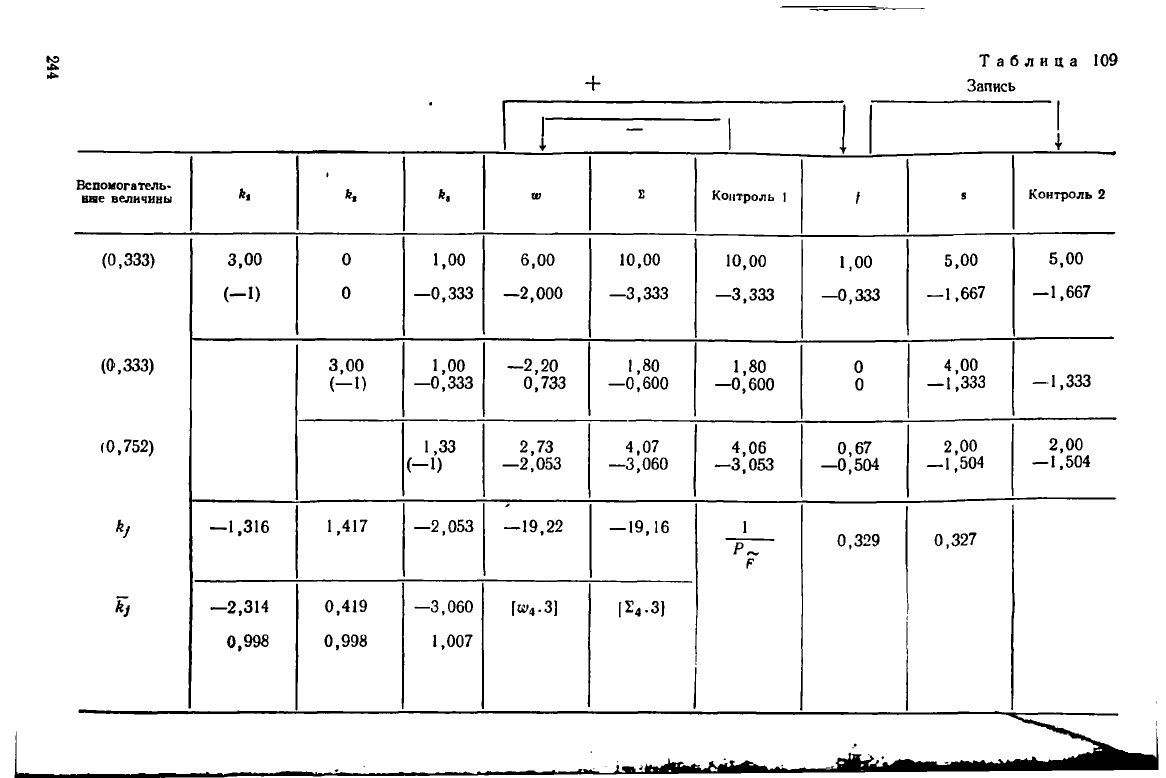
Таблица

109

Запись

! - !

Вспомогатель-

ные

величины

к,

к. к,

О)

Контроль

(0,333)

(0,752)

к)

3,00

(-1)

1,00

—0,333

6,00

—2,000

10,00

—3,333

10,00

—3,333

1,00

—0,333

5,00

—1,667

5,00

—1,667

(0,333)

(0,752)

к)

3,00

(-1)

1,00

—0,333

—2,20

0,733

1,80

—0,600

1,80

—0,600

4,00

—1,333

(0,333)

(0,752)

к)

1,33

(-1)

2,73

—2,053

4,07

—3,060

4,06

—3,053

0,67

—0,504

2,00

—1,504

2,00

—1,504

(0,333)

(0,752)

к)

—1,316

1,417

—2,053

—19,22

— 19,16 1

0,329

0,327

(0,333)

(0,752)

к)

—2,314

0,998

0,419

0,998

—3,060

1,007

[ю«-3]

|Г

.3]

0,329

0,327

то

= 0 1),

( 0,166 —0,167

, \в

ы-

вг = 0,666.

0,500),

Поэтому согласно формуле (4.50) рХ = 1 — 0,666 = 0,333 (не-

совпадение с формулой (4.48) вызвано ошибками округлений при вы-

числениях).

Если оценивается сразу несколько, например т, функций, то мат-

рица / имеет т строк, каждая из которых составляется отдельно для

каждой функции из элементов

V ду,

(у' = 1, 2,...,т; 1 = 1, 2,..., п).

Тогда вместо формулы (4.49) получим

= /р-1/

_ /Р-1В

• Ы-

ВР~

и вместо формулы (4.50)

Р-

=Ц

— {В

ВГ.

Наконец, если функциями являются уравненные измерения, то / =

= Е, где Е — единичная матрица порядка п. Тогда

лхл

р~»

р-1 _ р-1 ^ Л/"

5 Р'

для неравноточных и

Р~

= Е — В

Ы~

(4.51)

ЕГЫ^В =

для равноточных измерении.

Так, в рассмотренном примере матрица

0,668 + 0,166 + 0,166 + 0,335 — 0,167 — 0,167'

0,416 0,416 —0,167 0,083 0,083

0,416 —0,167 0,083 0,083

0,668 + 0,166 + 0,166

0,416 0,416

0,416]

и матрица обратных весов уравненных углов по формуле (4.51)

0,332 —0,166 —0,166 —0,335 + 0,167 + 0,167

0,584 — 0,416 + 0,167 — 0,083 — 0,083

0,584 + 0,167 — 0,083 — 0,083

0,322 — 0,166 — 0,166

0,584 —0,416

0,584,

242.

4.15. Доказать, что матрица уравненных углов в треугольнике

-1 2 -1 , (4.52)

У 3 ^—

— !

)

а в п- угольнике

—

. . . — П

-1

п—

. , . —

Р~= — \ • (4.53)

у п

Отсюда, в частности, следует, что отношение весов уравненного и неурав-

ненного угла

уI п

Равенство (4.54) в среднем выполняется для любых геодезических построе-

ний.

§ 42. НЕКОТОРЫЕ ВИДЫ УСЛОВНЫХ УРАВНЕНИЙ В ГЕОДЕЗИЧЕСКИХ

СЕТЯХ

Рассмотрим наиболее часто встречающиеся виды условных урав-

нений, возникающих в геодезических сетях, хотя с некоторыми из них

мы уже знакомы.

I. Нивелирные сети. В этом случае условные уравнения

называют полигонными, так как составляют их для выбранных в сети

полигонов, число которых совпадает с числом избыточных измерений

и равно г = I — к, где / — число ходов, к — число узловых точек.

Полигоны могут быть разомкнутые (опираться на исходные пункты)

или замкнутые. В общем виде условное уравнение имеет вид

2 ±

+ 00) = 0.

<6/

где означает суммирование поправок тех превышений, которые

'в/

входят в данный полигон. Знак «+» ставится, если направления хода

и полигона совпадают, знак «—» — если направления не совпадают.

Невязка

Щ = 2 ± + #нач — Я„о„-

/6/

Для замкнутых полигонов #

нач

= Я

кон

, поэтому Ю] — 2 ±

•е/

± Н

Необходимо отметить, что полигоны не должны быть линейно за-

висимы между собой, т. е. ни один из них не должен являться комби-

нацией других. Примеры таких условных уравнений мы уже при-

водили в § 38.

246.

В случае если полигонные

условные уравнения имеют коэф-

фициенты ±1 или 0, нормаль-

ные уравнения можно получить,

не составляя условных уравне-

ний. При этом схему сети необ-

ходимо предварительно подго-

товить, пронумеровав на ней все

ходы от 1 до / и полигоны от 1

рис 65

до г = / — т, где т — число

узловых точек. Следует выбрать

также направления ходов и полигонов, по которым будут суммиро-

ваться превышения, и выписать измеренные величины (сумму углов

или превышений) и обратные веса ходов (например, число углов или

длины ходов). Сделав это, нормальные уравнения составляют по

простым и'удобным правилам, предложенным проф. В. В. Поповым:

а) квадратичные коэффициенты нормальных уравнений в строке /

равны сумме обратных весов ходов, принадлежащих /-му полигону;

б) неквадратичные коэффициенты, расположенные в строке Н

и столбце /, равны обратному весу хода, принадлежащего полигонам

Н и /, причем взятому со знаком «+», если направления этих поли-

гонов совпадают, и «—» в противном случае;

в) свободный член /-го нормального уравнения равен невязке

/-го полигона.

Ясно, что каждому /-му полигону (условному уравнению) соответ-

ствует /-я коррелата.

Решив нормальные уравнения, получают все коррелаты и затем

поправки в измеренные в каждом ходе величины (в сумму углов или

превышений) по правилу: поправка у* равна обратному весу •к

, ум-

ноженному на сумму коррелат тех полигонов, которым принадлежит

1-й ход, причем если направления хода и полигона не совпадают, то

коррелата берется с обратным знаком. Так, для сети (рис. 65) имеем

нормальные уравнения

(тс

ТС

+ Тс

) к

— К

—

1г

/г

щ=0;

Определив из решения уравнений (4.55) коррелаты, поправки вы-

числим по формулам

V, «= — г

, у

= Г

(к

— к

), а, = 1Г

(к

— к

) и т. д.

Для оценки точности отметок узлов выбирают весовой полигон

от исходной точки до оцениваемого узла. Дополнительный столбец

в схеме Гаусса тогда получается по тем же правилам, по которым со-

ставляются нормальные уравнения. Например, если для оценки точ-

ности отметки узла I выбрать полигон, совпадающий с первым ходом,

то получим

—7Г

/г

—К

+(тс

+ я

+ш

= 0.

(4.55)

247.

[пс[] = —1Г

;

Ы] = 0, [тг^/1 = 0;

МЯ = 0; [тг/Л =

В матричной форме для элементов матрицы N нормальных уравне-

ний коррелат можно написать формулы

При этом весовой полигон нумеруется последним. После составления

матрицы N в ней нужно выделить последний столбец и строку, отно-

сящиеся к этому полигону, т. е. представить ее в виде

Обратный вес можно получить по формулам — = [л//- г] или

II. Триангуляционные построения. Линейные

(угловые) условные уравнения

1) Истинные значения углов, измеренных в плоском треугольнике,

должны удовлетворять исходному уравнению связи

называемое условным уравнением фигуры, где невязка равна

т. е. разности между суммой измеренных углов и 180° (теоретической

суммы).

2) Условное уравнение жесткого угла (например, рис. 66) выра-

жает требование У, + У

+ У

— ^АОВ = 0 и имеет вид V

4 VI 4 V, 4 ш = 0, где по = У1 + у

Ут

— ^АОВ.

3) Условное уравнение горизонта возникает на пункте, когда на

нем измерены все углы, имеющие общие стороны. Это условное урав-

нение применительно к рис. 67 имеет вид 4 V

4 о

4 и> = 0,

где невязка т = у

4 у

+ у

— 360°.

Если в сети измерены не углы, а направления, то условное урав-

нение горизонта не возникает.

4) Если в сети триангуляции содержатся жесткие дирекционные

углы сторон, не имеющие общих пунктов, то возникает условное

уравнение дирекционных углов. Например, для так называемой це-

почки треугольников (рис. 68) оно имеет вид

= Л/

, = — к

СеН,

] '

— = — Щ Ы-

Ф(Г) = У

+ Г

+ У

-180°=0,

которому согласно (4.19) соответствует уравнение

Щ + Щ 4 0

4 О) = 0,

ш = Ф (й. Уг> Уз) =

У1

+ Уг + Уз ~

180

°>

V^ + V

+ V

+ V^ + V

+ V

+ О) = 0,

248.

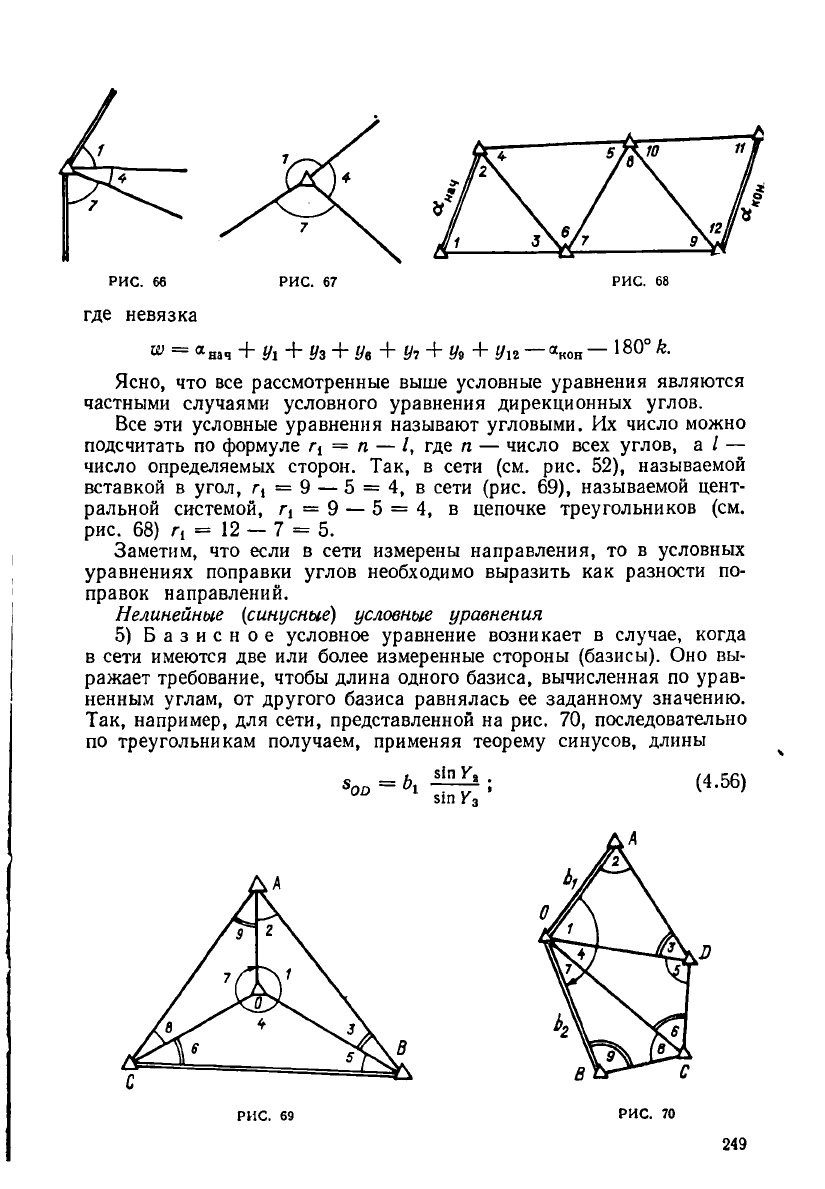
РИС. 66 РИС. 67

РИС. 68

где невязка

о» = «на, + Ух + Уз + у

+ у? + у

+ Уп — «кон —

180

Ясно, что все рассмотренные выше условные уравнения являются

частными случаями условного уравнения дирекционных углов.

Все эти условные уравнения называют угловыми. Их число можно

подсчитать по формуле г

= п — /, где п — число всех углов, а / —

число определяемых сторон. Так, в сети (см. рис. 52), называемой

вставкой в угол, г, = 9 — 5 = 4, в сети (рис. 69), называемой цент-

ральной системой, = 9 — 5 = 4, в цепочке треугольников (см.

рис. 68) г

= 12 — 7 = 5.

Заметим, что если в сети измерены направления, то в условных

уравнениях поправки углов необходимо выразить как разности по-

правок направлений.

Нелинейные (синусные) условные уравнения

5) Базисное условное уравнение возникает в случае, когда

в сети имеются две или более измеренные стороны (базисы). Оно вы-

ражает требование, чтобы длина одного базиса, вычисленная по урав-

ненным углам, от другого базиса равнялась ее заданному значению.

Так, например, для сети, представленной на рис. 70, последовательно

по треугольникам получаем, применяя теорему синусов, длины

(4.56)

РИС. 69

РИС. 70

249.

= («7)

Пекле объединения формул (4.56), (4.57) и (4.58) в одну приходим

к выражению

51П У

51П

5!П У

_ |

81П

5Ш У

51П

или, после логарифмирования,

18^ — 16 + 2 1в8шК,— 2 1§51пУ

=0, (4.59)

(=2,5,9 ;==3, 6, 9

представляющему собой исходное уравнение связи Ф(К,, У

, ..., У

) =

= 0, имеющее в отличие от всех предыдущих случаев нелинейный вид.

Коэффициенты приведенного к линейному виду условного урав-

нения согласно обозначению (4.16) найдем по формуле

, /д!вмпУЛ М соз и! М .

й[ = ± —2- ' =± — = ±

I дУ, )У

=У

Р" вшу; р"

где М = 0,43 — модуль перехода от десятичных логарифмов к нату-

ральным, а знаменатель р" = 206 265 введен по той причине, что в гео-

дезии поправки в углы вычисляют в угловой мере (в секундах). Вели-

чину ^ с1§ ух обычно обозначают через Д

(не путать с истинными

ошибками). Так как

18 5111

(у, + 1") = \&з1пу

+ — С18И,

то величина

А; = 51П (у

(

+ 1") — 18 51П ух (4.60)

есть изменение логарифма синуса угла с изменением угла на одну се-

кунду и может быть получена из таблиц логарифмов тригонометри-

ческих функций (обычно применяют семизначные таблицы Вега) как

табличная разность Л, уменьшенная в 10 раз (шаг таблиц Н — 10").

Обычно достаточно выражать в шестом знаке логарифма, поэтому

Д, = Л/100.

После линеаризации выражения (4.59) будем иметь условное урав-

нение

+ Д

— Д

— Д„у

— Д

+ га = 0. (4.61)

Можно указать следующее правило составления базисного услов-

ного уравнения: 1) выбираем направление подхода от базиса Ьх к ба-

зису Ь

, 2) последовательно по каждому треугольнику намечаем у,глы,

лежащие против передней и задней по ходу стороны (эти углы назы-

ваются связующими, они показаны соответственно одной и двумя дуга-

ми), 3) пишем условное уравнение в общем виде, ставя знаки «+» и

250

. !

«—» перед ДI соответственно тому, каким является угол у

— перед- •

ним или задним. С помощью указанных таблиц находим величины

А/ и вычисляем невязку

т =

81П у

з!п \)ъ з1п_Ув_

> (4<62)

81п у

81П у

31П у

Вычисления выполняем в специальной таблице.

Следует заметить, что в настоящее время в вычислениях широко

внедряются калькуляторы (мин-компьютеры), например, такие, как

«Электроника БЗ-18». Поэтому таблицы применяются все реже и реже.

В этой связи уравнение (4.61) преобразуем к виду

(=2, о. 8 г—3, 6, 9

умножив его на коэффициент

к = =4,749427 • 10

или в более общей записи

2±С18И»1 + Й> = 0, (4.63)

165

где через я обозначено множество связующих углов. Условное урав-

нение (4.63) более приспособлено для составления его с помощью

мини-компьютеров*. Оно может служить также для контроля состав-

ления уравнения (4.61).

6) Так называемое полюсное условное уравнение возникает

в сети триангуляции, в которой имеется замкнутая относительно ка-

кой-либо стороны цепочка треугольников (см., например, рис. 69).

Оно составляется точно так же, как и базисное, с той разницей, что

базисы и Ь

здесь совпадают с одной из сторон и поэтому в вычисле-

нии невязки их длины не участвуют (т. е. для возникновения полюсного

условного уравнения совсем не должны быть измерены какие-либо

стороны). Точку О называют полюсом (на этой точке могут быть из-

мерены все углы, хотя это и не обязательно), а направление обхода

выбирают от одной из сторон, например ОА, исходящей из полюса,

и к ней же подходят. Так, на рис. 69 полюсное условное уравнение

также имеет вид (4.61), причем невязка

XI) = 31П У2 З'П Уъ 51П у„ ^

з1п 03 51П у

31П у,

7) Координатные условные уравнения возникают в сети триангу-

ляции, в которой имеется 5 изолированных групп исходных пунктов.

Их число г = 2 (5 — 1). Так, в цепочке треугольников (см. рис. 69)

* В прил. XIII.7 приведена программа для калькулятора «Электроника

БЗ-21».

251.

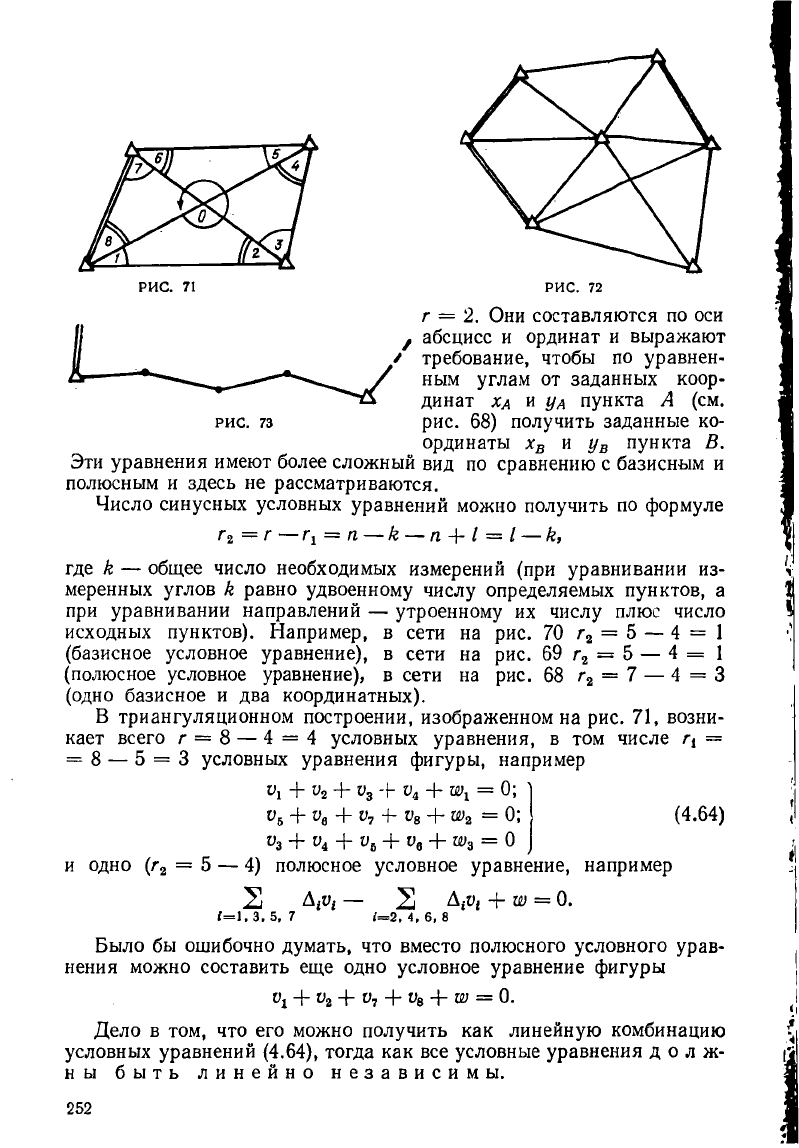
РИС. 71 РИС. 72

г = 2. Они составляются по оси

абсцисс и ординат и выражают

требование, чтобы по уравнен-

ным углам от заданных коор-

динат ХА И ул пункта А (см.

РИС. 73 рис. 68) получить заданные ко-

ординаты х

и у

пункта В.

Эти уравнения имеют более сложный вид по сравнению с базисным и

полюсным и здесь не рассматриваются.

Число синусных условных уравнений можно получить по формуле

=г—г

= п — к — п + 1 = 1 — к,

где к — общее число необходимых измерений (при уравнивании из-

меренных углов к равно удвоенному числу определяемых пунктов, а

при уравнивании направлений — утроенному их числу плюс число

исходных пунктов). Например, в сети на рис. 70 г

= 5 — 4 = 1

(базисное условное уравнение), в сети на рис. 69 г

= 5 — 4 = 1

(полюсное условное уравнение), в сети на рис. 68 г

= 7 — 4 = 3

(одно базисное и два координатных).

В триангуляционном построении, изображенном на рис. 71, возни-

кает всего г = 8 — 4 = 4 условных уравнения, в том числе —

= 8 — 5 = 3 условных уравнения фигуры, например

«1 + + У

4 + щ = '

5 + V* +

7 + щ + ПУ

= 0; (4.64)

щ + + + + щ = 0

и одно (г

= 5 — 4) полюсное условное уравнение, например

2 — 2 + го = 0.

{=1.3.5,7 (=2.4,6,8

Было бы ошибочно думать, что вместо полюсного условного урав-

нения можно составить еще одно условное уравнение фигуры

+ Щ + + +

ХЮ

= 0.

Дело в том, что его можно получить как линейную комбинацию

условных уравнений (4.64), тогда как все условные уравнения долж-

ны быть линейно независимы.

252.

Существуют и взаимно заменяемые условные уравнения. Так, в

построении на рис. 68 условные уравнения базисное и дирекционных

углов можно заменить двумя координатными условными уравнениями

(составляемыми от пункта С к О) и наоборот.

Во всех случаях следует стремиться к тому, чтобы условные урав-

нения имели наиболее простой вид и содержали как можно меньше

общих измерений (последнее обстоятельство приводит к уменьшению

вычислительных погрешностей при решении нормальных уравнений).

На рис. 72 изображена сеть триангуляции. Сколько возникает

в ней угловых и синусных уравнений. Какие это уравнения?

III. Полигонометрические сети. При уравнива-

нии полигонометрических сетей условные уравнения чаще всего со-

ставляют для отдельных ходов, входящих в сеть. В каждом ходе

(рис. 73) возникает три условных уравнения. Уравнение дирекци-

онных углов имеет вид

п'

8а„

•

(4.65)

1= I

где 6а

нач

и 6а

кон

— поправки приближенных значений

направлений, а невязка

узловых

= «пач — «кон + ^ Р* лев ~

180° к.

(4.66)

Если а

нв

, _и а

кон

безошибочны, то поправки ба

нач

и ба

равны нулю. Два условных уравнения координат имеют вид

У«

соза

(

+ — +

р 1

ч®

нач

1кон^

кон~Ь

*нач —

кои Н Лкон^В + = 0,

Р ^

2°.

81П а

- ^ I

нач^нач

+ -1

>кон®

кон +

</нач —

</к он + = 0,

где центральные координаты

"Чг

Уг

—

Уц>

— х

(4.67)

(

а координаты центра тяжести хода, если углы равноточны,

У1+У2 + ...+ У

. [у]

Уп =

*1 + +

• • •

+ V

п'

(4.68)

253.