Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

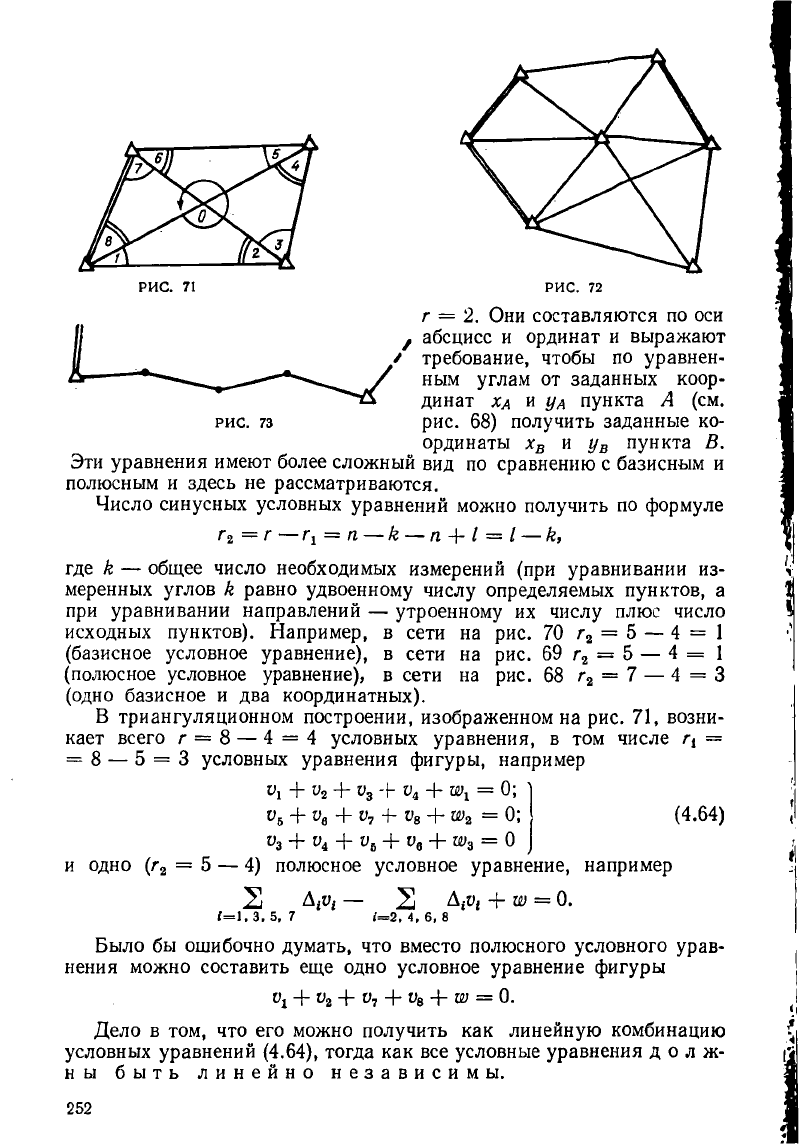
РИС. 71 РИС. 72

г = 2. Они составляются по оси

абсцисс и ординат и выражают

требование, чтобы по уравнен-

ным углам от заданных коор-

динат ХА И УА пункта А (см.

РИС. 73 рис. 68) получить заданные ко-

ординаты х

и у

пункта В.

Эти уравнения имеют более сложный вид по сравнению с базисным и

полюсным и здесь не рассматриваются.

Число синусных условных уравнений можно получить по формуле

=г—г

= п — к — п + 1 = 1 — к,

где к — общее число необходимых измерений (при уравнивании из-

меренных углов к равно удвоенному числу определяемых пунктов, а

при уравнивании направлений — утроенному их числу плюс число

исходных пунктов). Например, в сети на рис. 70 г

= 5 — 4 = 1

(базисное условное уравнение), в сети на рис. 69 г

= 5 — 4 = 1

(полюсное условное уравнение), в сети на рис. 68 г

= 7 — 4 = 3

(одно базисное и два координатных).

В триангуляционном построении, изображенном на рис. 71, возни-

кает всего г = 8 — 4 = 4 условных уравнения, в том числе —

= 8 — 5 = 3 условных уравнения фигуры, например

Щ + 0

+ Vз + + щ = 0; '

5 + V* +

7 + 08 + го

= 0; (4.64)

0з + 04 + 0

+ + Щ = 0

и одно (г

= 5 — 4) полюсное условное уравнение, например

2 — 2 Д(0( + го = 0.

{=1.3.5,7 (=2.4,6,8

Было бы ошибочно думать, что вместо полюсного условного урав-

нения можно составить еще одно условное уравнение фигуры

01 + 02 + 07 + 08 + ГО = 0.

Дело в том, что его можно получить как линейную комбинацию

условных уравнений (4.64), тогда как все условные уравнения долж-

ны быть линейно независимы.

251.

Существуют и взаимно заменяемые условные уравнения. Так, в

построении на рис. 68 условные уравнения базисное и дирекционных

углов можно заменить двумя координатными условными уравнениями

(составляемыми от пункта С к О) и наоборот.

Во всех случаях следует стремиться к тому, чтобы условные урав-

нения имели наиболее простой вид и содержали как можно меньше

общих измерений (последнее обстоятельство приводит к уменьшению

вычислительных погрешностей при решении нормальных уравнений).

На рис. 72 изображена сеть триангуляции. Сколько возникает

в ней угловых и синусных уравнений. Какие это уравнения?

III. Полигонометрические сети. При уравнива-

нии полигонометрических сетей условные уравнения чаще всего со-

ставляют для отдельных ходов, входящих в сеть. В каждом ходе

(рис. 73) возникает три условных уравнения. Уравнение дирекци-

онных углов имеет вид

п'

8а„

•

(4.65)

1= I

где 6а

нач

и 6а

кон

— поправки приближенных значений

направлений, а невязка

узловых

= «пач — «кон + ^ Р< лев ~

180° к.

(4.66)

Если а

нв

, _и а

кон

безошибочны, то поправки ба

нач

и ба

равны нулю. Два условных уравнения координат имеют вид

У«

соза

(

+ — +

р 1

ч®

нач

1кон^

кон~Ь

*нач —

кон Н Лкон^В + = 0,

Р ^

2°.

81П а

- ^ I

нач^-^нач

+ -1

>кон®

кон +

</нач —

</к он + 1й)

= 0,

где центральные координаты

"Чг

Уг

—

Уц>

— х

(4.67)

(

а координаты центра тяжести хода, если углы равноточны,

У1+У2 + ...+ У

. [у]

Уп =

• • •

+ V

п'

(4.68)

252.

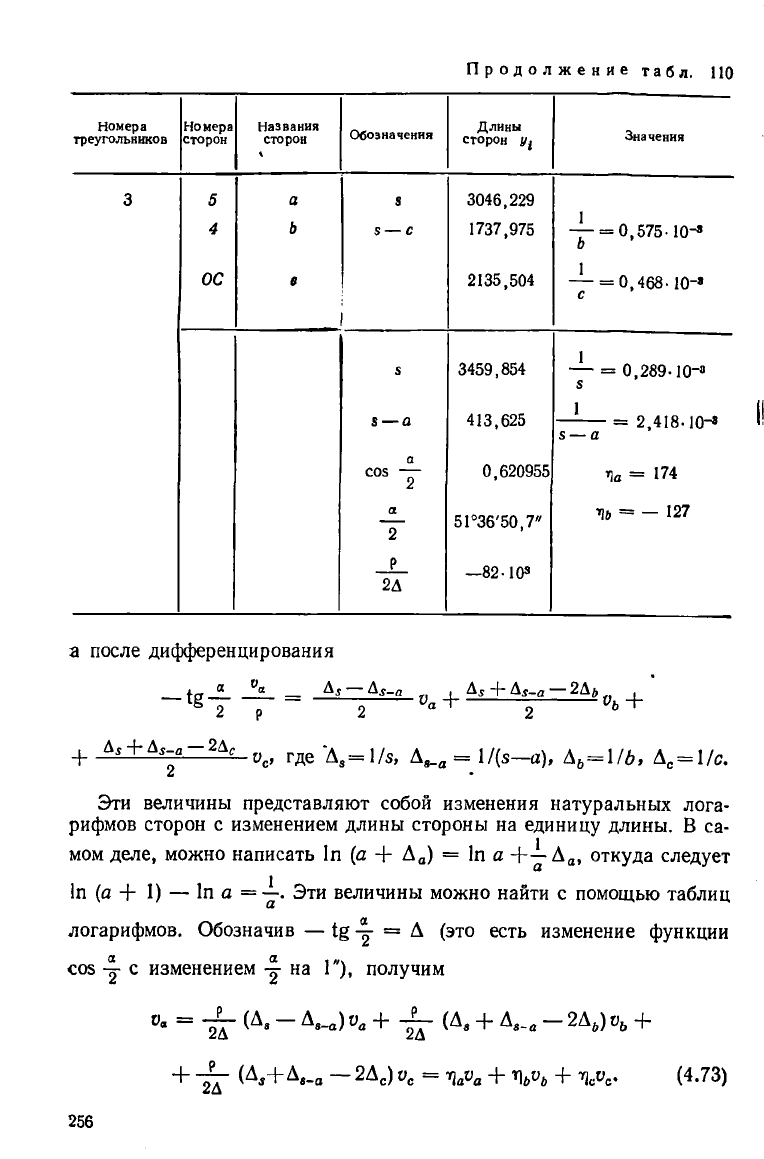
Продолжение табл. 110

Номера

треугольников

Номера

сторон

Названия

сторон

Обозначения

Длины

сторон Ух

Значения

3 5

8 3046,229

5 —

1737,975

- = 0,575-10-»

ОС

в 2135,504

- = 0,468.10"»

3 3459,854

- = 0,289- Ю

-3

— а

413,625

— а

413,625

5 —

— 2,41В-10 *

соз

0,620955

•Па

= 174

51°36'50,7"

Ч» = — 127

2Д

—82-10

а после дифференцирования

— 1а — А. - — ,, . + Д^-а — 2А» '

+ + р

, где А

= 1/з, А_

= 1/(5—а), Д

=1/6, А

= 1/с.

2, •

Эти величины представляют собой изменения натуральных лога-

рифмов сторон с изменением длины стороны на единицу длины. В са-

мом деле, можно написать 1п (а + А

) = 1п а +—А

, откуда следует

1п (а + 1) — 1п а = Эти величины можно найти с помощью таблиц

логарифмов. Обозначив — = Д (это есть изменение функции

соз ^ с изменением на Г), получим

Х>л =

~к

{А

> ~

Ав

а) х>а +

~к

(Л

+А

2Аь) +

+ Л_о - 2Д

) = Г\аО

+ Т)Л + Чв»е. (4-73)

256

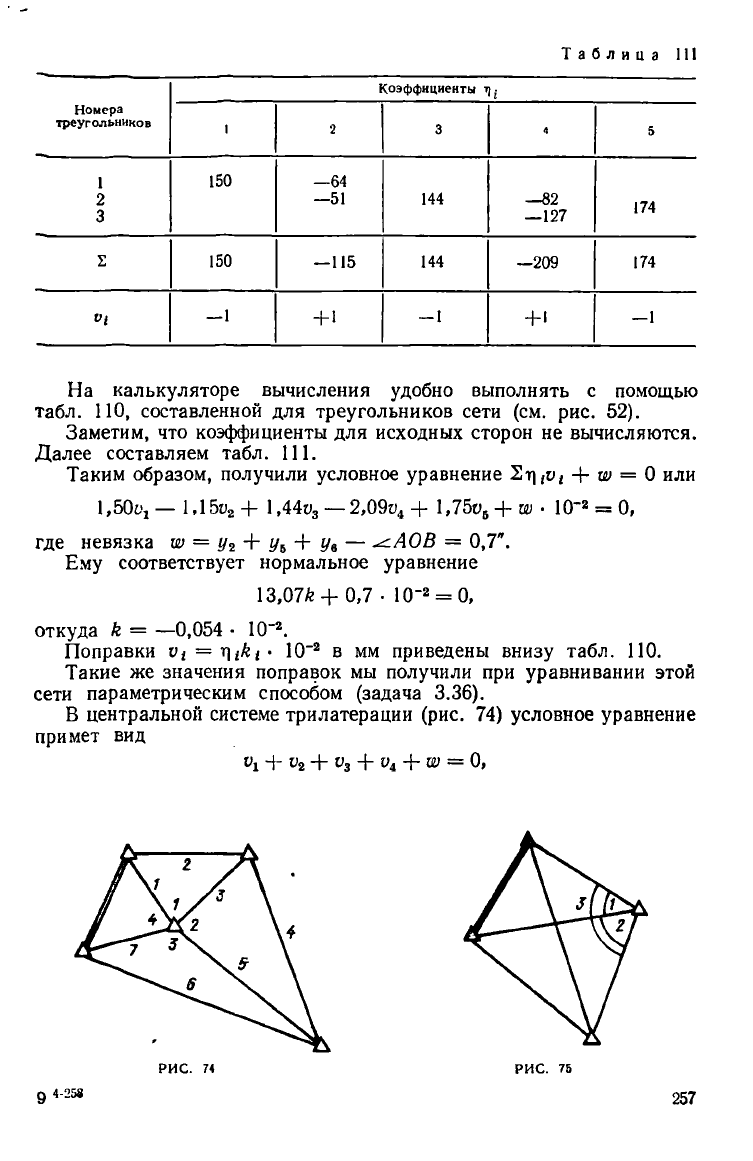
Таблица

143

Коэффициенты т)

;

Номера

треугольников

150

—64

—51

144

—82

—127

174

150

—115

144

—209

174

—1

+ 1

— 1

—1

На калькуляторе вычисления удобно выполнять с помощью

табл. 110, составленной для треугольников сети (см. рис. 52).

Заметим, что коэффициенты для исходных сторон не вычисляются.

Далее составляем табл. 111.

Таким образом, получили условное уравнение + ш = 0 или

1,500,- 1.150,+ 1,44у

— 2,09о

+ 1,75е

+ и>. 10"

= 0,

где невязка т = у

+ у

— ^АОВ = 0,7".

Ему соответствует нормальное уравнение

13,076 + 0,7 • 10"

= 0,

откуда к = —0,054 • 10"

Поправки = "Пс * Ю

-2 в мм

приведены внизу табл. 110.

Такие же значения поправок мы получили при уравнивании этой

сети параметрическим способом (задача 3.36).

В центральной системе трилатерации (рис. 74) условное уравнение

примет вид

^ +

1>2

+ Щ + 0

= 0,

9 4-258

257

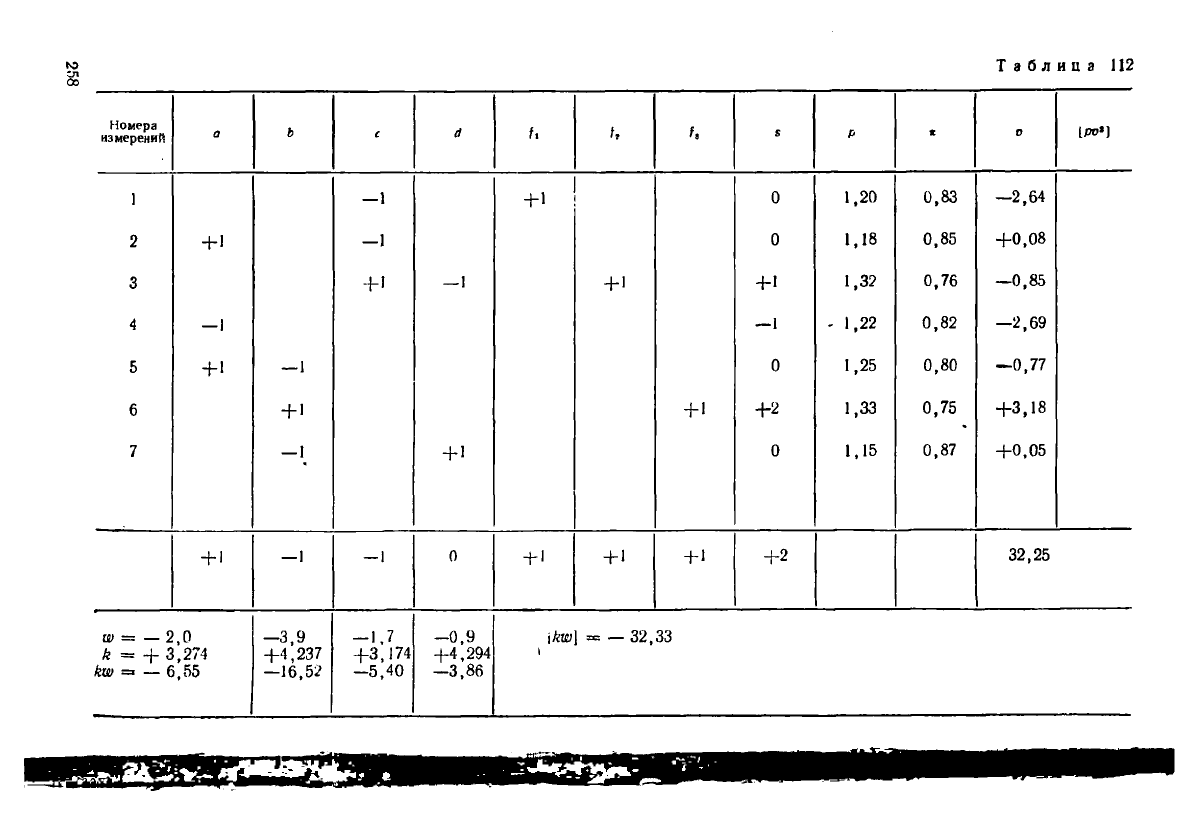
Таблица 143

Номера

измерений

с в

и 1,

1 ро»)

—1

1,20

0,83

—2,64

+ 1

—1

1,18 0,85

+0,08

+ 1

—1

+ 1

1,32 0,76

—0,85

— 1

— 1 - 1,22

0,82 -2,69

+ 1

— 1

0 1,25

0,80

—0,77

+ 1

+2 1,33 0,75

+3,18

—

+ 1

1,15

0,87

+0,05

+ 1

—1 — 1

+ 1

32,25

да = — 2,0

к = +

3,274

= — 6,55

-3,9

+4,237

—16,52

— 1,7

+3,174

—5,40

-0,9

+4,294

-3,86

/да] = —

32,33

а в системе с пересекающимися диагоналями (рис. 75)

Щ + Щ—Щ + до = О,

которое можно составить для любой вершины.

4.16. Определить, допустима ли невязка условного уравнения, составлен-

ная в рассмотренном выше примере уравнивания сети трилатерации, если сторо-

ны были измерены с точностью а = 0,02 м. Установить точность углов у

, уь,

г/

. вычисленных по измеренным длинам сторон.

Ответ: 3,2"; 3,5"; 4".

4.17. В задаче 4.16 вычислить все остальные углы каждого треугольника и

установить точность их определения. Найти корреляционные матрицы вычислен-

ных углов в каждом треугольнике и углов у

, уь, у

§ 43. ЗАДАЧИ НА УРАВНИВАНИЕ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ

КОРРЕЛАТНЫМ СПОСОБОМ

4.18. Уравнять нивелирную сеть (см. задачу 3.48) [10]. В этой сети возни-

кает г = 7 — 3=4 условных уравнения или полигона, показанных на рис. 66.

Решение

Условные уравнения полигонов имеют вид

— 04 + 06 + ^1 = 0, -0,-02 + 03+0)3 = 0,

— Vь+О

—

+ Щ = 0, — 0

+О

+Ш

= О.

Оценим также точность функций — отметок реперов 1, 2 и 3, составив весо-

вые функции по ходам 1, 3 и 6 (весовые полигоны). В табл. 112, 113 приведены

коэффициенты условных и нормальных уравнений.

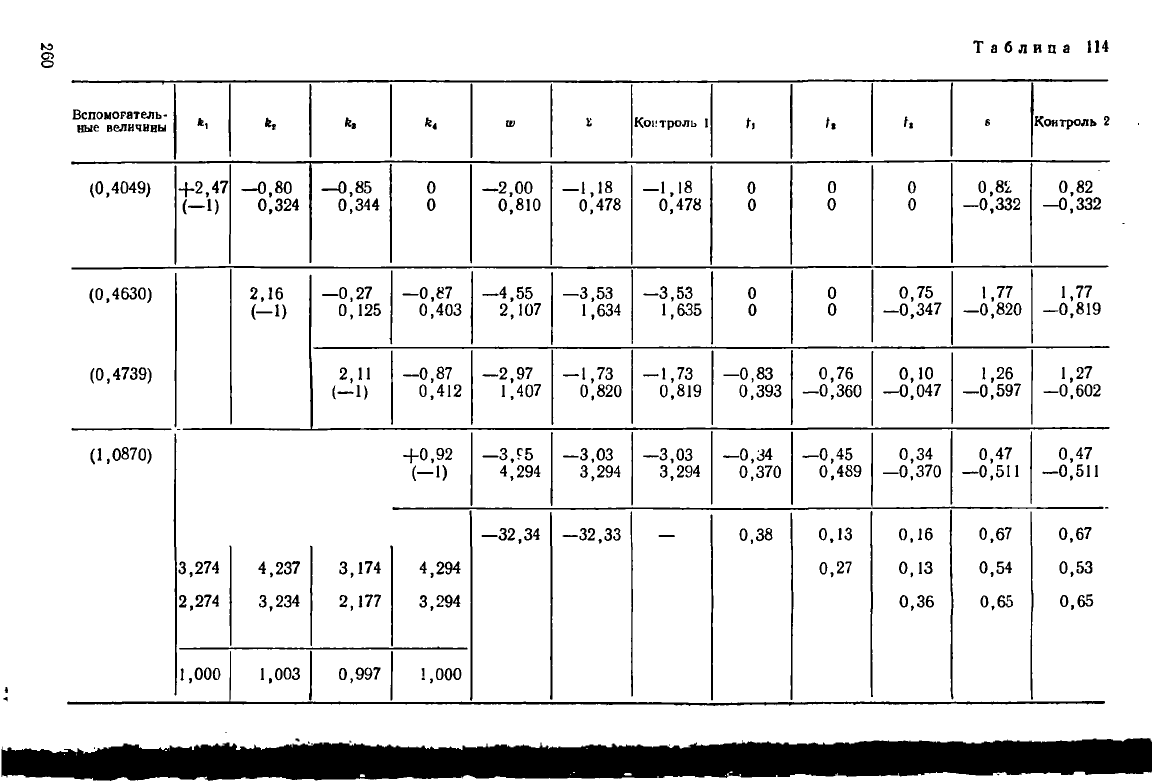
Решение нормальных уравнений по схеме Гаусса выполнено в табл. 114.

Обратим внимание, что последняя схема предусматривает двойной контроль.

Второй контроль получается вычитанием из чисел в графе «контроль 1» чисел

из графы ю и прибавлением чисел из граф /

Контроль вычисления обратных весов (или матрицы ) выполняется так

же, как и в параметрическом способе.

По найденным значениям коррелат в табл. 112 получены поправки и произ-

веден заключительный контроль вычислений: = —[кт\.

После введения поправок V, в измеренные значения получены уравненные

значения превышений и отметок реперов

й, = + 6,108

, А

= +8,343

, А

= + 5,605

А, = + 1,367,, Л

=-6,976,, Л

= —0,898

А, = +6,078

= 189,614,, Я

= 197,958

, Н

= 190,981

Таблица 113

а]

Ь]

г] <<]

Конт-

роль

1-а

\г.Ь

[КС

Ыз

2,47

—0,80

2,42

—0,85

2,44

—0,87

—0,76

1,63

—0,83

0,83

0,76

—0,76

0,76

0,75

0,82

1,50

0,76

—0,76

0,76

1,50

0,82

1,50

0,76

-0,76

0,76

1,50

—2,00

—3,90

— 1,70

—0,90

-1,18

—3,15

—0,87

—0,90

259

Таблица

143

Вспомогатель-

ные

величины

к,

к.

Контроль

и 1,

Г.

Контроль

(0,4049) +2,47

(-1)

—0,80

0,324

—0,85

0,344

—2,00

0,810

-1,18

0,478

-1,18

0,478

0,82

—0,332

0,82

—0,332

(0,4630)

2,16

(-1)

—0,27

0,125

—0,87

0,403

—4,55

2,107

—3,53

1,634

—3,53

1,635

0,75

—0,347

1,77

—0,820

1,77

—0,819

(0,4739)

2,11

(-1)

—0,87

0,412

—2,97

1,407

— 1,73

0,820

— 1,73

0,819

—0,83

0,393

0,76

—0,360

0,10

—0,047

1,26

-0,597

1,27

-0,602

(1,0870)

+0,92

(-1)

—З.Р5

4,294

—3,03

3,294

—3,03

3,294

—0,34

0,370

—0,45

0,489

0,34

—0,370

0,47

—0,511

0,47

—0,511

—32,34

-32,33

—

0,38 0,13 0,16

0,67

3,274

4,237

3,174

4,294

0,27

0,13

0,54 0,53

2,274 3,234

2,177

3,294

0,36 0,65

0,65

1,000 1,003

0,997

1,000

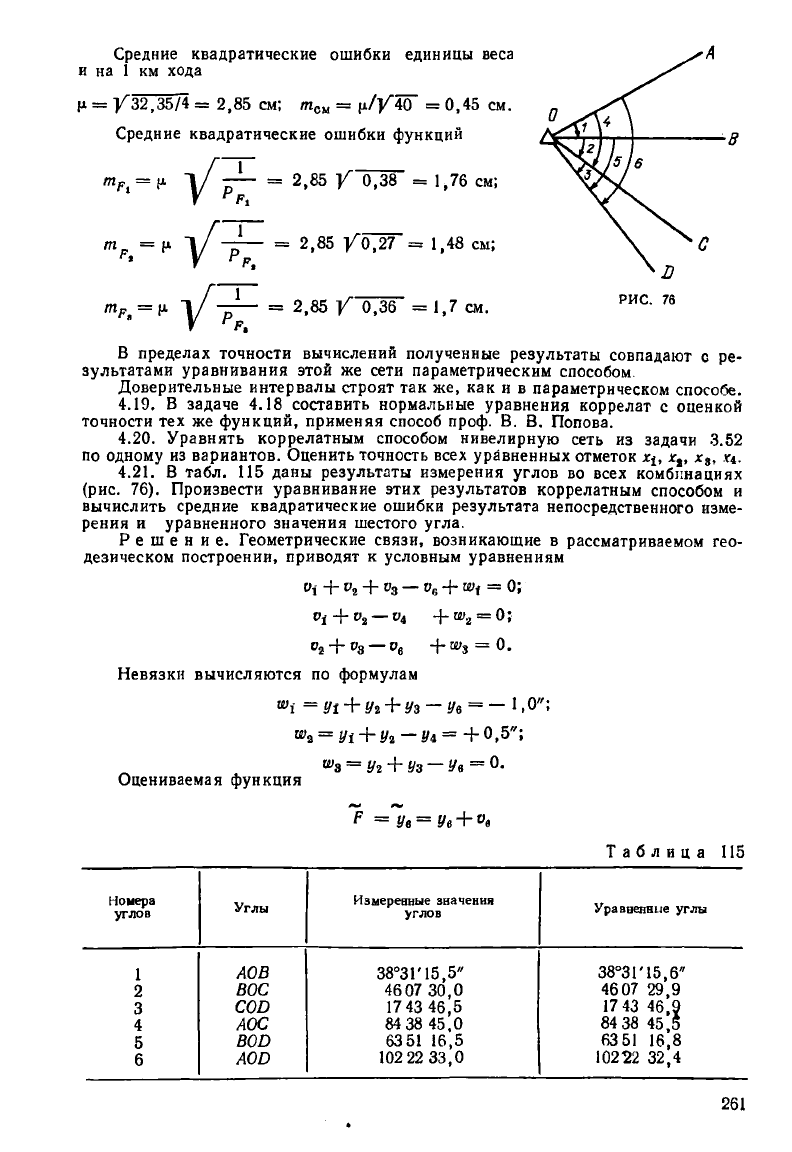
Средние квадратические ошибки единицы веса

и на 1 км хода

= 1/32,35/4= 2,85 см; т

см

= ц/уЧо =0,45 см.

Средние квадратические ошибки функций

т,

76 см;

= 2,85 =

^ У^

= 2,85= 1,48 см:

"у/"-^- =

•

V 0736~ = 1,7 см.

5 6

•л

РИС. 76

В пределах точности вычислений полученные результаты совпадают с ре-

зультатами уравнивания этой же сети параметрическим способом.

Доверительные интервалы строят так же, как и в параметрическом способе.

4.19. В задаче 4.18 составить нормальные уравнения коррелат с оценкой

точности тех же функций, применяя способ проф. В. В. Попова.

4.20. Уравнять коррелатным способом нивелирную сеть из задачи -3.52

по одному из вариантов. Оценить точность всех уравненных отметок *{, х

4.21. В табл. 115 даны результаты измерения углов во всех комбинациях

(рис. 76). Произвести уравнивание этих результатов коррелатным способом и

вычислить средние квадратические ошибки результата непосредственного изме-

рения и уравненного значения шестого угла.

Решение. Геометрические связи, возникающие в рассматриваемом гео-

дезическом построении, приводят к условным уравнениям

щ + °г + °з —

*>г,

®1

= о;

Р^ +

Р-8

—о

+ а»

= 0;

"г +

— +

о>з

= 0.

Невязки вычисляются по формулам

Щ=У1 +

У*

УЗ

—

У*

= —1 .0":

Щ =

У1

Уг

— </4= +0,5";

Щ =

У2

Уз

—

У«

= 0.

Оцениваемая функция

Ув

= Ув +

Таблица 115

Номера

углов

Углы

Измеренные значения

углов

Уравненные углы

АОВ

ВОС

СОй

АОС

ВОО

АОй

38°ЗГ15,5"

46 07 30,0

43 46,5

84 38 45,0

16,5

102 22 33.0

38°3г15,6"

46 07 29,9

17 43 46.9

84 38 45,5

16,8

10222 32,4

261.

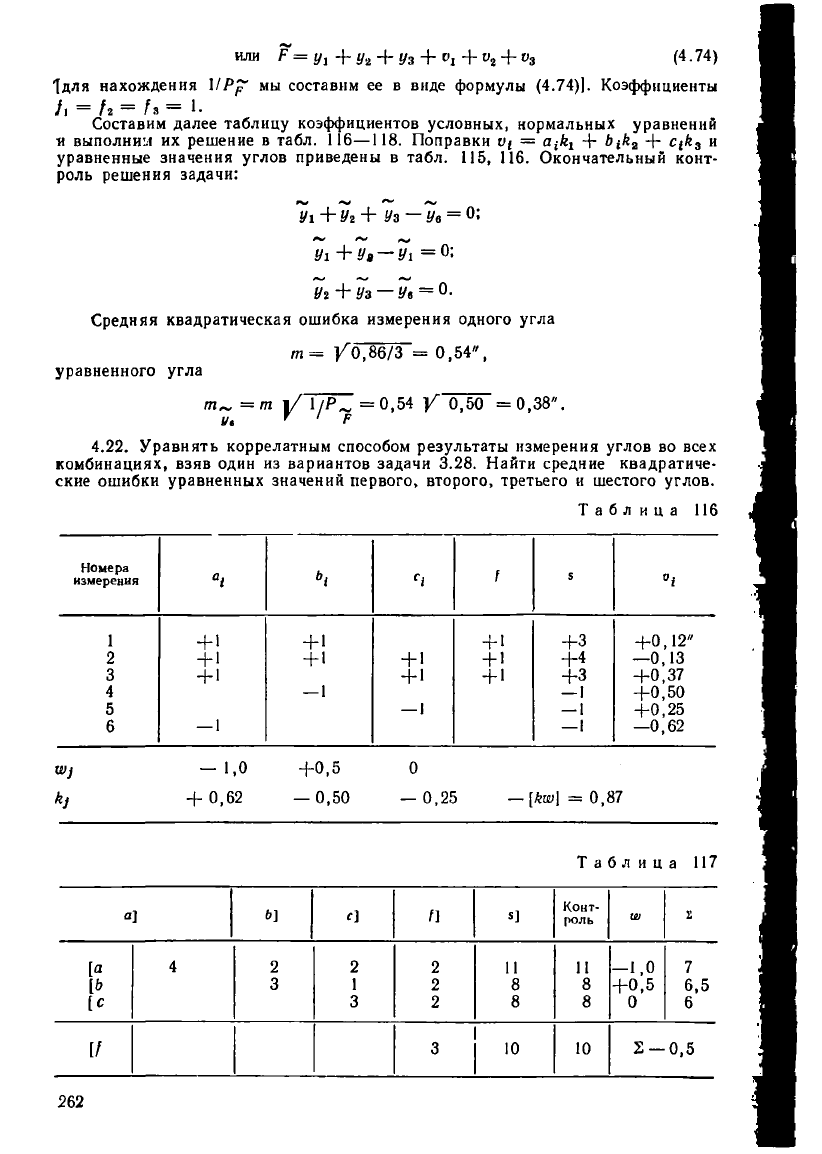
или Р = У\ +

Уч

+ Уз + 01 + ^ + ь

(4.74)

1для нахождения I/Рр' мы составим ее в виде формулы (4.74)]. Коэффициенты

/, = /. = /.= 1-

Составим далее таблицу коэффициентов условных, нормальных уравнений

и выполни:.! их решение в табл. 116—118. Поправки О; = а

+ + С(й

уравненные значения углов приведены в табл. 115, 116. Окончательный конт-

роль решения задачи:

+2/г+ Уз

*Ув

О»

У1+Уа —

У1

Уг +

Уз

—

У»

Средняя квадратическая ошибка измерения одного угла

т = 0,86/3 = 0,54",

уравненного угла

т„=т ^/1/ЯГ = 0,54 К~0Ж = 0,38".

4.22. Уравнять коррелатным способом результаты измерения углов во всех

комбинациях, взяв один из вариантов задачи 3.28. Найти средние квадратиче-

ские ошибки уравненных значений первого, второго, третьего и шестого углов.

Таблица 116

Номера

измерения

»1

°1

+ 1

+ 1 + 1

+0,12"

+ 1

+ 1 + 1

—0,13

+ 1 +1 + 1

+0,37

4 —1

— 1 +0,50

—1

— 1 +0,25

— 1

— 1 —0,62

— 1,0 +0,5 0

к, + 0,62 — 0,50 — 0,25 — [М = 0,87

Таблица 117

с]

Конт-

роль

[а

2 2

11 11

— 1,0 7

[Ь

3 1

2 8

+0,5

6,5

[с

8 8

3 10 10

2 —

0,5

262.

Таблица 118

Вспоыога•

тельнь'е

велнчнгы

Их

А.

Конт-

роль 1

Конт-

роль 2

(—0,250)

4.0

(-1)

2,0

—0,50

2,0

—0,50

-1,0

—0,25

7,0

— 1,75

7,0

— 1,75

3,0

—0,75

11,0

—2,75

11,0

—2,75

(—0,500)

2,0

(-П

1,0

-0,50

3,0

—1,50

3,0

—1,50

0,5

—0,25

2,5

—1,25

2,5

— 1,25

(—0,500)

2,0

(-0

0,5

—0,25

2,5

—1,25

2,5

-1,25

0,5

—0,25

2,5

—1,25

2,5

— 1,25

0,62

—0,28

—0,50

—1,50

—0,25

—1,25

—0,87 —0,87

РЕ

0,50 0,50

1,00

4.23. Уравнять коррелатным способом углы, измеренные в сети триангу-

ляции (см. задачу 3.38), и оценить точность уравненной стороны СБ (см. рис.

52). Исходные данные: 1е&х = 3.258 4263, = 3.329 5004, ^ВОА = 224°19'

40,5".

Решение. В этой сети возникает г = 9 — 4=5 условных уравнений,

в том числе:

3 условных уравнения фигур

"1 + + °3 + = 0.

"4 + + "в + Щ =

От

«9

+ Щ =

;

1 уравнение жесткого угла

+ 05 +

О*

+ ^4 = 0,

1 уравнение базисное

ЛЛ — Аз»з + Д404 — Д

"в + А?"? — Д9О9 + Щ = 0.

Вычисление невязок условных уравнений выполняют в табл. 119—121.

Условие базисов в линейном виде (коэффициенты и свободный член выраже-

ны в единицах 6-го знака логарифма)

+ 1,00(1) — 1,80(3) + 1,46(4) — 0,79(6) + 3,15(7) — 2,26(9) + 10,8 = 0.

При составлении базисного условного уравнения направление обхода вы-

брано от базиса Ь

к базису

Так как весовая функция и базисное условное уравнение одинаковы по ви-

ду, то весовая функция для стороны составляется точно так же и по тем же пра-

вилам, что и базисное условное уравнение, с той лишь разницей, что сневязка»

не вычисляется, так как величина /

не оказывает влияния на оценку точности.

Для нашей задачи, выбрав направление подхода к стороне ОС от базиса Ь

}

получим весовую функцию

Р = /о — Д,^ + Д

— Д

+ Д

263