Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.


Продолжение табл. 96
«<э>
„(4)
*/
4
5)
*<
7)
Х
1
,(8)
Х
1
0,40
—0,38
-1,18
0,37
—0,41
—1,20
0,35
—0,43
-1,21
0,340
—0,434
— 1,214
0,338
—0,436
—1,215
0,337
—0,437
—1,216
Обычно метод Зейделя дает лучшую сходимость, чем метод простой
итерации, хотя это бывает не всегда.
Отметим, что в геодезии для уравнивания геодезических сетей
часто применяют методы приближений, располагая вычисления на
схеме сети и полагая последовательно все пункты, за исключением
одного, исходными. Нетрудно показать, что по существу это тоже есть
метод Зейделя, только оформленный в иной вычислительной схеме.
Представляется, однако, что рассмотренная здесь схема более удобна
и поэтому упомянутые способы применять нецелесообразно.
Легко понять, что для получения обратной матрицы (}, необходи-
мой для оценки точности в параметрическом способе, также можно
применить метод простой итерации или Зейделя, приняв столбцы
свободных членов равными —как и в методе Гаусса (см. § 30).
3.61. Методом простой итерации и Зейделя найти с точностью до 0,01 по-
следний столбец матрицы ф для системы нормальных уравнений (3.86)
3.62. Можно ли применить для решения системы нормальных уравнений
3 2 1 \ /8*, \ / 0,5 \
2 4 2 ){ Ьх
г
) =[ 0,5 ) . (3.87)
1 2 3 / \ одгд / \ 1,0/
составленной в задаче 3.17, метод простой итерации?
3.63. Решить систему (3.87) по методу Зейделя. Получить также матрицу
О = Я"
1
.
3.64. Решить по методу итераций и Зейделя одну из систем нормальных
уравнений из задачи 3.18.
3.65. В угломерном ходе с п поворотными точками составить в общем виде
уравнения поправок и матрицу коэффициентов нормальных уравнений, приняв
в качестве неизвестных поправки дирекционных углов сторон. Можно ли полу-
ченную систему решать по способу простой итерации? Найти по этому методу
первую, вторую и третью строки обратной матрицы. Обнаружив простую зако-
номерность в образовании этих строк, написать всю обратную матрицу.
Глава 4.
КОРРЕЛАТНЫЙ СПОСОБ УРАВНИВАНИЯ
§ 38. ВЗАИМОСВЯЗЬ ПАРАМЕТРИЧЕСКОГО И КОРРЕЛАТНОГО СПОСОБОВ
УРАВНИВАНИЯ
Коррелатный способ уравнивания может быть выведен из пара-
метрического способа следующим образом. Напишем уравнения по-
224

правок так, чтобы первые к уравнений можно было разрешить относи-
тельно к неизвестных бдгу, т. е. чтобы поправка представляла собой
линейную функцию поправок = 1, 2, ..., к). Эту систему пред-
ставим так:
= ЯцС*! + а
12
о
г
+ .
Ьх
2
= + а
22
и
2
+ .
• + <4*»* + «01;
• + +
а
02
;
<к = +
а
А2«2 +
• + «**»* +
а
Ой-
(4.1)
Полученные поправки подставим в оставшиеся г = п—к уравне-
ний поправок. Тогда получим г уравнений, неизвестными в которых
будут только поправки Эти уравнения запишем в виде
а,о
1
+ а
2
V
2
+
Ь
1
ь
1
+ 6
2
о
2
+
+ щ = 0;
+ + щ = 0;
+ № + • • • + ёп^п + щ = 0
(4.2)
и назовем их условными уравнениями.
Излагая указанную процедуру в матричной форме, запишем си-
стему уравнений поправок А Ах + Ь = V в виде двух уравнений
А
х
Ах + Ь
х
= V» (4.3)
А
2
Ах + Ь
2
=У
г
, (4.4)
в которых матрица А
х
квадратная порядка к и имеет обратную мат-
рицу А~\. Матрица А
2
имеет размер г X к. Из уравнения (4.3) находим
вектор
Ах = А~
1
У
х
— А~
1
1
Х
(4.5)
[в подробной записи это система (4.1)]. Подставляя вектор (4.5) в урав-
нение (4.4), получим
откуда
где
А
2
(А~
1
У
1
-А~
1
+ =
У
1
-У
г
+ № = 0,
Г = Ь
2
-А
2
А~
1
1
х
.
Уравнение (4.6) можно переписать в виде
где Е — единичная матрица порядка г, а блочная матрица
(А
г
А~'—Е) =В •
гхл
8- <"258
(4.6)
(4.7)
(4.8)
(4.9)
225

РИС. 61 РИС. 62
С этим обозначением систему- перепишем в виде
+ № = 0. (4.10)
Если матрицу В представить так:
/а, а
2
. . .с
Я=
Ь
\ •
>6п
I. (4.11)
то (4.10) в подробной записи будет иметь вид (4.2).
Пример 1. Перейти от параметрического способа к коррелат-
ному при уравнивании трех углов, измеренных в треугольнике
(рис. 61). В качестве необходимых неизвестных выберем углы 1 и 2.
Тогда уравнения поправок будут
= 8лг
х
+ V, V
2
= 8*2 + /
2
; «3 = — — +
1
3-
Приняв в качестве приближенных значений = у
и
= у
ъ
где ух — измеренные значения углов, будем иметь свободные члены
1
1 =
0, /
2
= 0 и /
3
= 180° — у
х
— у
2
— у
3
= —да,
где
хю
— так называемая невязка. Поэтому
V! = у
2
= Ьх
г
; V
3
= —
8дг,
— 8*, — хо.
В этой системе матрицы
= = А~
Х
=Е\ = -1).
Поэтому согласно формулам (4.9) и (4.7) находим В = (—1 —1 —1),
а) = Ь
2
= —№ и, наконец, получаем условное уравнение
— V
1
— у
2
—1)
3
—
по
= 0,
или
Р
1
+ 1>2 + 1>
3
+
М>
= 0. (
4
-
12
)
Пример 2. Перейти от параметрического способа уравнивания
к коррелатному в нивелирной сети (рис. 62). Здесь уравнения попра-
вок имеют вид;
226.
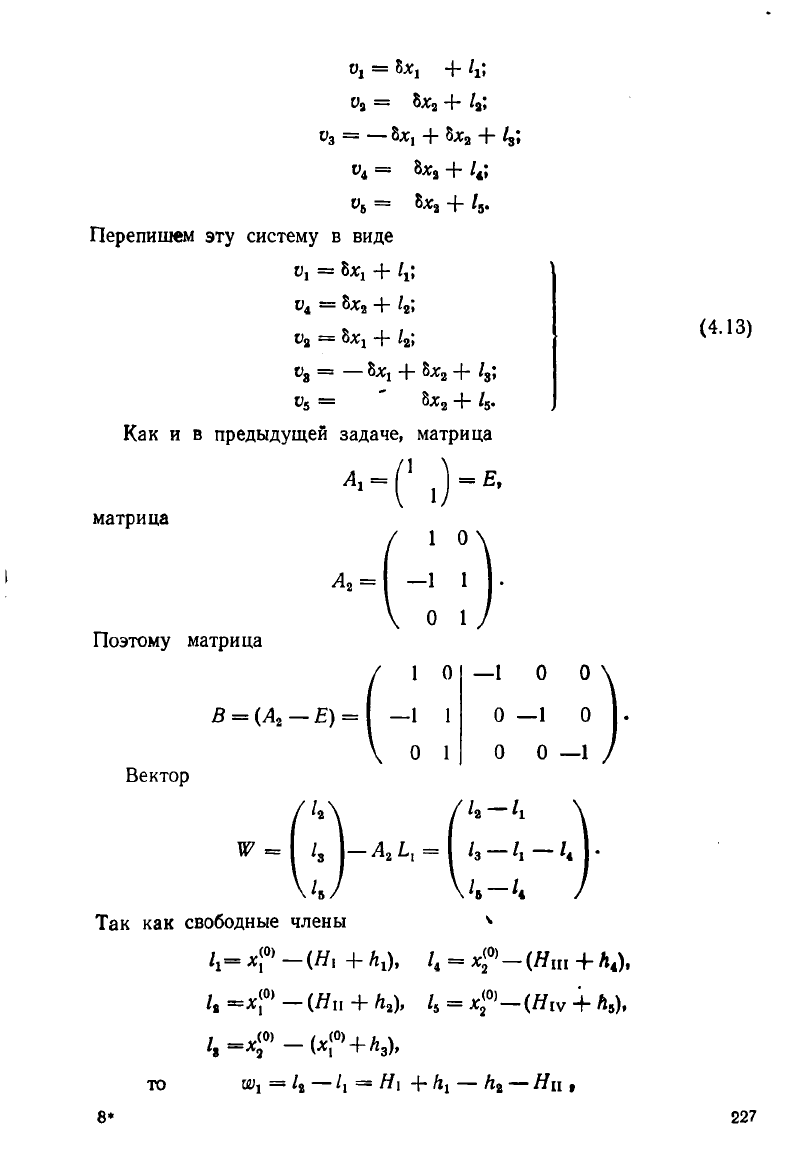
= +
1Ц
1>
а
= 8х
2
+ /
а
;
у
3
= —&*,+ 8дс
2
+ /
3
;
1*4 = +
= 8*2 + /
5
.
Перепишем эту систему в виде
V
^
= 8*, + 1ц
= +
1
г>
V
2
= 8х, + /
2
;
г, = — 5л;, + 8х
2
+ /
3
;
г
5
= " 8х
2
+ /
5
.
Как и в предыдущей задаче, матрица
Л,
матрица
Поэтому матрица
(4.13)
Вектор
V
л/
Так как свободные члены *
/
1=
*;
о>
- (я, + л
г
), и = +л
4
),
,(0)
- (//и + А,), /
5
= Х™-(Н
1У
+ Л
в
),
щ = — /] = Н\ 4- Л, — Л
2
— Ни ,
то
7*
227
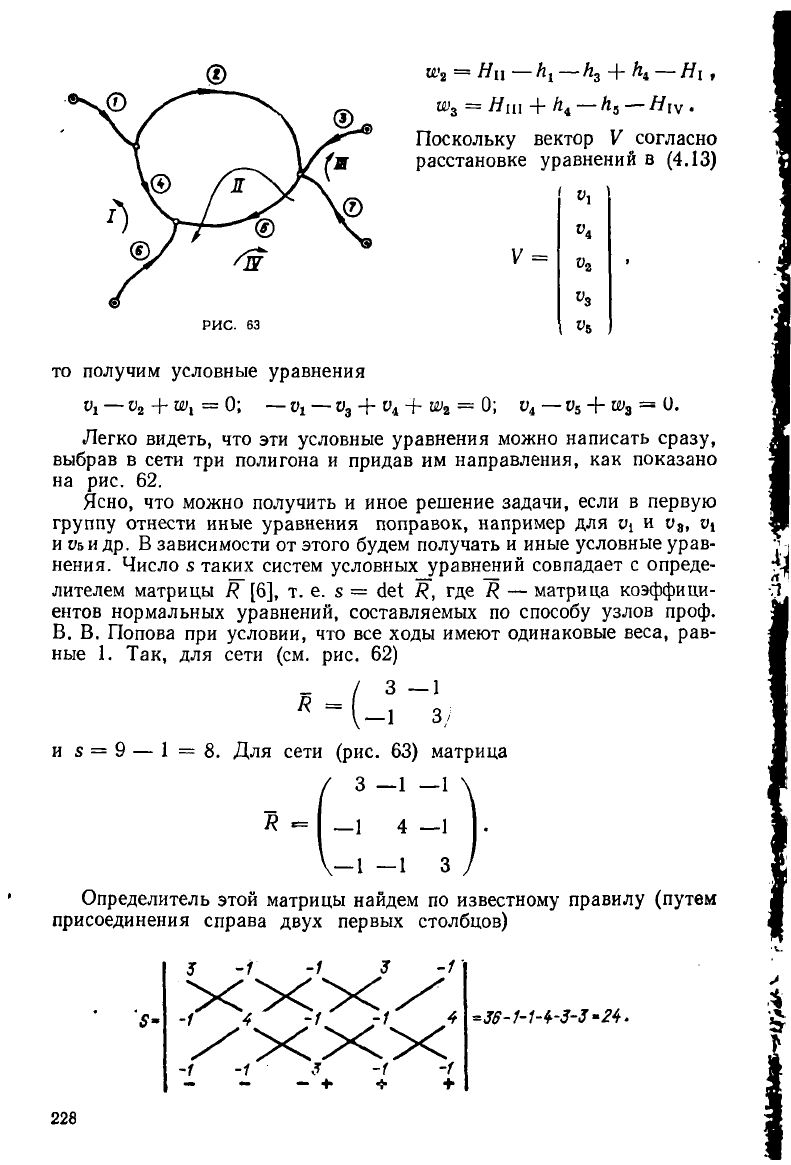
®
а<
2
= Н
и
—Л, —Н
3
+ Л
4
— Н
х
,
Поскольку вектор К согласно
расстановке уравнений в (4.13)
Щ = Н
ш
+ к
х
— Н
ь
— Н
1У
.
РИС. 63
УБ
то получим условные уравнения
V
1
— V
2
+ щ = 0•, ——а
3
+ с
4
+ ш
2
= 0; у
4
—и
5
+ ау
3
= 0.
Легко видеть, что эти условные уравнения можно написать сразу,
выбрав в сети три полигона и придав им направления, как показано
на рис. 62.
Ясно, что можно получить и иное решение задачи, если в первую
группу отнести иные уравнения поправок, например для и V
3
,
и
У5
и др. В зависимости от этого будем получать и иные условные урав-
нения. Число 5 таких систем условных уравнений совпадает с опреде-
лителем матрицы Н [6], т. е. 5 = ёе! где Я — матрица коэффици-
ентов нормальных уравнений, составляемых по способу узлов проф.
В. В. Попова при условии, что все ходы имеют одинаковые веса, рав-
ные 1. Так, для сети (см. рис. 62)
Определитель этой матрицы найдем по известному правилу (путем
присоединения справа двух первых столбцов)
и 5 = 9 — 1 = 8. Для сети (рис. 63) матрица
5 -Г -1 3 -1
-1 4 -1-1 4 =36-1-1-4-3-3-24.
<! -1 I
- +• •}• +
-1
+
228.

Таблица 81 Таблица 83
Номер дерева
Ветви дерева
;з
14
15
16
17
18
19
20
21
22
23
24
3,
7.
3,
7,
6,
1,
7,
3,
2,
2,
1,
1.
Номер дерева
Ветви дерева
1
1.
3,
6
2
1,
7,
6
3
1,
2,
6
4
1, 2,
4,
5
5
1,
2,
4,
5
6
1,
з,
4
7
1,
4,
7
8
6,
4,
2
9
6,
4,
3
10
6,
5,
2
11
6,
4,
7
12
6,
5, 1
Совокупность всех измерений, отнесенных в первую группу, на
языке теории графов называется деревом сети. Число таких деревьев
равно 5.
4.1. Составить деревья в сети (см. рис. 62) и по каждому дереву получить
систему условных уравнений.
4.2. Перейти к системе условных уравнений в нивелирной сети (см. рис. 64)
по одному из следующих деревьев (табл. 97).
Например, вариант 11 приведет к выбору полигонов, показанных на рис.
63.
4.3. Доказать, что матрицы коэффициентов условных уравнений и уравне-
ний поправок связаны соотношением ВА — 0. Проверить это свойство в задаче
4.2.
4.4. Перейти от уравнений поправок к условному уравнению в задачах
3.36, 3.37. Обращение и перемножение матриц выполнить на ЭВМ «Наири-К»
по стандартным программам.
4.5. Перейти от параметрического способа к коррелатному в сети триангу-
ляции с измеренными углами (см. рис. 52, задача 3.38), отнеся в первую группу
уравнения поправок для углов 2, 3, 7, 8, которых достаточно для однозначного
определения координат пунктов Д и С.
4.6. Исходя из параметрического способа, составить условные уравнения
при многократном измерении одной и той же величины.
Переход от параметрического способа к коррелатному выполняют в том слу-
чае, когда условные уравнения имеют сложный вид.
Переход от коррелатного способа к параметрическому делают значительно
реже и выполняют следующим образом. Из общего числа п поправок VI выбирают
к поправок и пишут выражения
о
1
= 8*
1
; о
2
— Ьх
2
, . . . ; ю
к
= Ьх
к
.
После этого систему условных уравнений записывают в виде
В
х
\х + В
2
У
2
+
П7
2
= 0
и выражают вектор
= — В'! ВуАх —В~- П7
2
.
Тогда получают систему уравнений поправок
V, = + У
г
= -4
2
Ах + Ц,
где матрицы
229

А
г
= — В-
1
В
и
1К-0, = — В^"
1
«7,.
4.7. Перейти от условного уравнения + + р, + да =• О (см. пример
1) к уравнениям поправок.
Решение. Пусть
тогда
8*! + 8*, + 0
Э
+ да = О,
откуда
Р
3
= — 8д;
1
—
Вдс
г
— да.
Уравнения поправок
"х = к, — = — 8*, — 8*, + /
8
,
где /
8
= —да.
4.8. Перейти от условных уравнений в примере 2 к уравнениям поправок.
§ 39. КОРРЕЛАТНЫЙ СПОСОБ УРАВНИВАНИЯ. УСЛОВНЫЕ
И НОРМАЛЬНЫЕ УРАВНЕНИЯ, ИХ РЕШЕНИЕ
Рассмотренные в предыдущем параграфе условные уравнения,
как правило, составляют независимо от параметрического способа
уравнивания, исходя из геометрических связей, возникающих в сети.
В самом деле, каждое избыточное измерение приводит к образованию
точной математической зависимости между истинными значениями
измеренных величин (условное уравнение связи)
ФуО^ У У„) = 0. (4.14)
Всего таких уравнений, которые назовем исходными уравнениями
связи, будет г = п — к. Например, если У
(
— углы треугольника, то
У.1 +У
г
+У
3
- 180° = 0.
Приводя (4.14) к линейному виду путем разложения в ряд Тей-
лора и приняв в качестве приближенных значений У= у
и
где
Ух — измеренные значения, получим
%(У1, У Уп)+
У1
(У, -Уд = 0.
(4.15)
1 = 1
Введя обозначения
=
0|
, =
Ь
, (&)
=
ЗУ1/1 \дУ1/о ' [дУг/о
= и>
/
= ч>,(у
1
, у
г
, . . ., у
п
) (4.16)
и учитывая, что разности у
{
— У
{
= А
{
есть истинные ошибки из-
мерений, вместо (4.15) напишем
230.

+ =
1=1
Уь
1
{-Ь) + Щ = 0,
1=1
2 ^ <—+= о.
1=1
(4.17)
Система (4.17), состоящая из г уравнений с п неизвестными, имеет
множество решений относительно Д Поэтому она не может быть
решена однозначно. Из всего множества решений выберем такие не-
известные (— Д
г
) та VI, которые удовлетворяют условию метода на-
именьших квадратов
или
Ф = [V
2
1 = гтпп
Ф = [ри
2
| = ппп
(4.18)
(4.18')
соответственно для равноточных и неравноточных измерений. Вели-
чины VI назовем поправками. Система
а,1>, + Ь
2
а
2
4- . . . + а„у„ + щ = 0, '
Ь
х
1>1
+ Ь
г
у
г
4- . . . + Ь„р
п
+ хю
2
= 0,
+ + • • • + ётРп + чу, = 0
(4.19)
носит название условных уравнений поправок (условных уравнений).
Для отыскания относительного минимума функций (4.18) и (4.18')
необходимо применить метод Лагранжа, согласно которому составляем
функцию
Фи
4
] +М1О0] + 0>х) + М(М + ю
2
) + . . . + Х
г
([я»] + и>,),
где — неопределенные пока множители Лагранжа. Беря производ-
ные от Ф по VI и приравнивая их к нулю, а также обозначая для удоб-
ства Яу = —2к), получаем после деления на —2 выражения
V
1
= а,Л, + Ь
х
к
2
+ . . . 4- д
г
к
г
,
V
2
= а
2
к
х
+ Ь
г
к
2
4- ... 4- д
2
к
г
,
и
п
= а
п
к
1
+ Ь
п
к
2
+ . . . + $
п
к
г
(4.20)
определяющие поправки через так называемые коррелаты к). Для
случая неравноточных измерений аналогично получим
231.

= — 4- Ь
х
к
2
+ . . . + |т,/г
г
),
Р\
0,= — (ОяЙ, + 6Л+ • • - + ЯЛ).
Рг Г*.^!)
с„ = — (аА + Мг 4- . . . +
Рп
Для определения коррелат к), подставив выражения (4.20) или
(4.21) в (4.19), получим соответственно для случая равноточных и не-
равноточных измерений систему уравнений
[аа\ к
х
+ \аЬ\ к
г
+ . . \а$\к
г
+ щ = О,
[аЬ]к
х
+ [ЬЬ\к
2
+ . . ,+ [Ь§]к
г
+ щ = 0,
• • • • •
(4.22)
или
(4.23)
Ш + к
2
+ . . . + {§§] к
г
+ т
т
= О
\паа] к
х
+ \тЬ\ к
2
+ . . . + [ад^] к
Т
+ ау, = О,
\паЬ\ к
х
+ \кЬЬ\ к
2
+ . . . + [ъЪц\ к
г
+ щ = О,
к, + \пЬ§| к
2
+ . , . + [гс^т] к
г
+ хи
г
= О,
где = — обратные веса.
Выражение (4.22) или (4.23) называют системой нормальных урав-
нений коррелат.
1
От аналогичной системы, возникающей в параметрическом спосо-
бе, она по виду отличается лишь свободными членами, которые теперь
не связаны с коэффициентами а
1у
Ь
{
, ..., Величины щ, вычислен-'
ные по формуле (4.16) и представляющие собой приближенные значе-
ния функций фу, вычисленных по измеренным значениям у
и
назы-
вают невязками условных уравнений.
В матричной форме условные уравнения (4.19) записываются в
виде
+ № = 0, (4.24)
а нормальные уравнения
МК + ЧР = 0, ' (4.25)
где матрица
\паа\ \ъаЪ\ . . . [па§]
N = ВР~
Х
В
т
=
аЬ] [КЬЬ]
' ' '
V = Р~
1
В
1
К,
что соответствует равенствам (4.21).
Вектор поправок
(4.25')
(4.26)
232.

В теории коррелатного способа уравнивания доказывается, что
- И
2
] = -
— [/и>
2
] = [да]
[там] \ъЬЬЛ)
(Г
~ I)
2
]
(4.27)
\щ(г-1)
2
][2, .(г-1)]
—
4
(4.28)
или
= К
+1
.Г] = [2г
+
1-П.
где величины
21 = 1
яаа
1 + \™Ь\ + . . . + [яа^] + юг = [»га5'| + ш,,
2г = + \кЬЬ\ + . . . + [кЬ§] + щ = |гб5'] + щ,
2, = + + • . . + + ау
г
= (я^! + ьи
г
,
(4.29)
(4.30)
а величины 5,- = а
(
-+-
Ь[ + ... +
Алгоритмы с одной буквой [до
2
.1], [се;
3
.2]... раскрываются точно
так же, как и алгоритмы [/
2
.1], [/з-2] и т. д. в параметрическом способе
уравнивания, например
|ш
2
. 11 = щ —
[ш
3
. 2] = щ
[ъаЬ\
Шл
[тага]
[лас]
и>1
[кЬс. 1] [ц>
2
.1]
[пЬЬ.1]
[паа]
и т.д. Раскрытие алгоритмов [2
2
.1], [2
3
.2]... выполняется по фор-
мулам
(V 1 I - V ГС'
2
! К.1][Е
2
.1)
12лА
1
~ ~ т^т \мл\
и т. д., подобно тому, как раскрываются аналогичные алгоритмы в
параметрическом способе.
Если условно обозначить
Щ = \раЦ>
Щ = I Р
Ь1
\>
(4.31)
ОУ, = \Р§1Ъ
ш
г
= |
Р
и\ = о
21 = \Р08\,
22 = [рЬз\,
• 94
(4.32)
2г 1/^5],
2г
+
1=1ау]=1р/5]»
233.
