Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

то алгоритмы [ш

.1], [хю

.2] и т. д., [2

.1], [2

.2] и т. д. будут раскры-

ваться так же, как и алгоритмы [рЫ. 1], [рс1.2] и т. д., 1], [рсз.2\

и т. д. в параметрическом способе уравнивания. Тогда вместо (4.27)

и (4.28) условно можно написать

[рх>

1 = [р11 . к]; — \р&\ = [р/

. к].

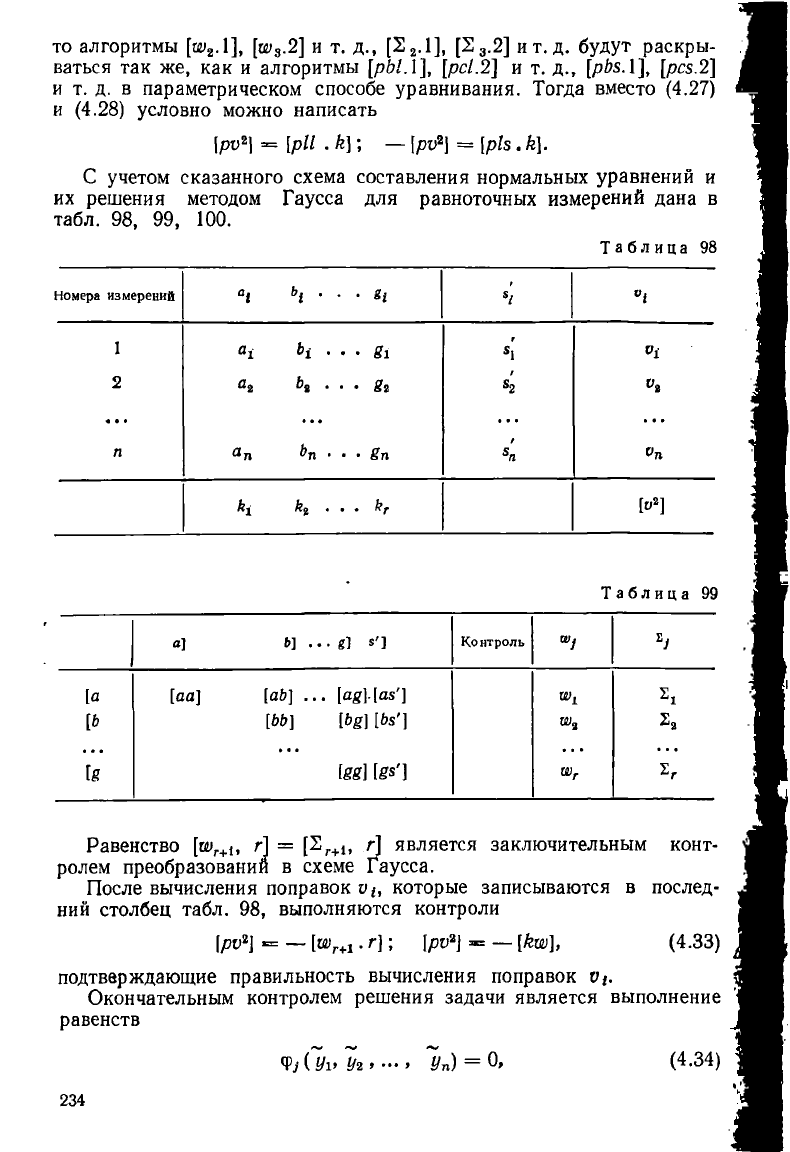
С учетом сказанного схема составления нормальных уравнений и

их решения методом Гаусса для равноточных измерений дана в

табл. 98, 99, 100.

Таблица 98

Номера измерений

1 •

• • «г

°1

Ьх •

• • 8х

«1

<*2

• ' 8г

«2

• • • 8п

*п

От»

кг

]

Таблица 99

а]

6] .

• •е! 8']

Контроль

Шу

[а

[аа]

[аЬ] ..

[Ь

[ЬЬ]

[Ь8] [Ьв']

[ 8

Равенство [ш

г+1

, г] = [2

г+1

, г1 является заключительным конт-

ролем преобразований в схеме Гаусса.

После вычисления поправок которые записываются в послед-

ний столбец табл. 98, выполняются контроли

\р&\ = - [а»

г+1

. г]; \р&\ - - [кт], (4.33)

подтверждающие правильность вычисления поправок с*.

Окончательным контролем решения задачи является выполнение

равенств

«М^» ~Уп) = 0, (4.34)

234.

Таблица 81 Таблица 83

Вспомога-

тельные

величины

А.

к, . . .

Контроль

<!/[««])

[аа]

[аЬ] ..

[ей

—1

\аЬ]

[«*]

И>,

—1

[аа]

\аа]

(1/[66.1]) [66.1] ...

[Ьё-Ц

К.1]

[Ьв.1]

К-1] [2,-1]

[66.1]

(г

-1)]

К(г-1)]

(г-1)]

-1

[ю

(г-1)]

[№(/—1)]

[И ('-Ш

К ...

А,

[Щ+1

. =

—

к, ...

1 ... 1

где

Уг = У г +

— уравненные значения измеренных величин. Иными словами, не-

вязки всех условных уравнений, вычисленных по уравненным резуль-

татам измерений, должны быть равны нулю.

Часто применяют такие контрольные формулы:

[сю] =

[Ьо] = — щ ,

= _ П1

(4.35)

Следует, однако, заметить, что они контролируют лишь правиль-

ность вычисления поправок. Однако если в вычислении коэффициентов

условных уравнений допущены ошибки, что особенно вероятно, когда

исходные функции (4.14) нелинейные, геодезическая сеть окажется

неупавненной даже при соблюдении равенств (4.35). Над столбцами и>

и 2 в табл. 100 делают такие же преобразования, как и под столб-

цами / и 5 в параметрическом способе. Коррелаты к

}

вычисляются

235

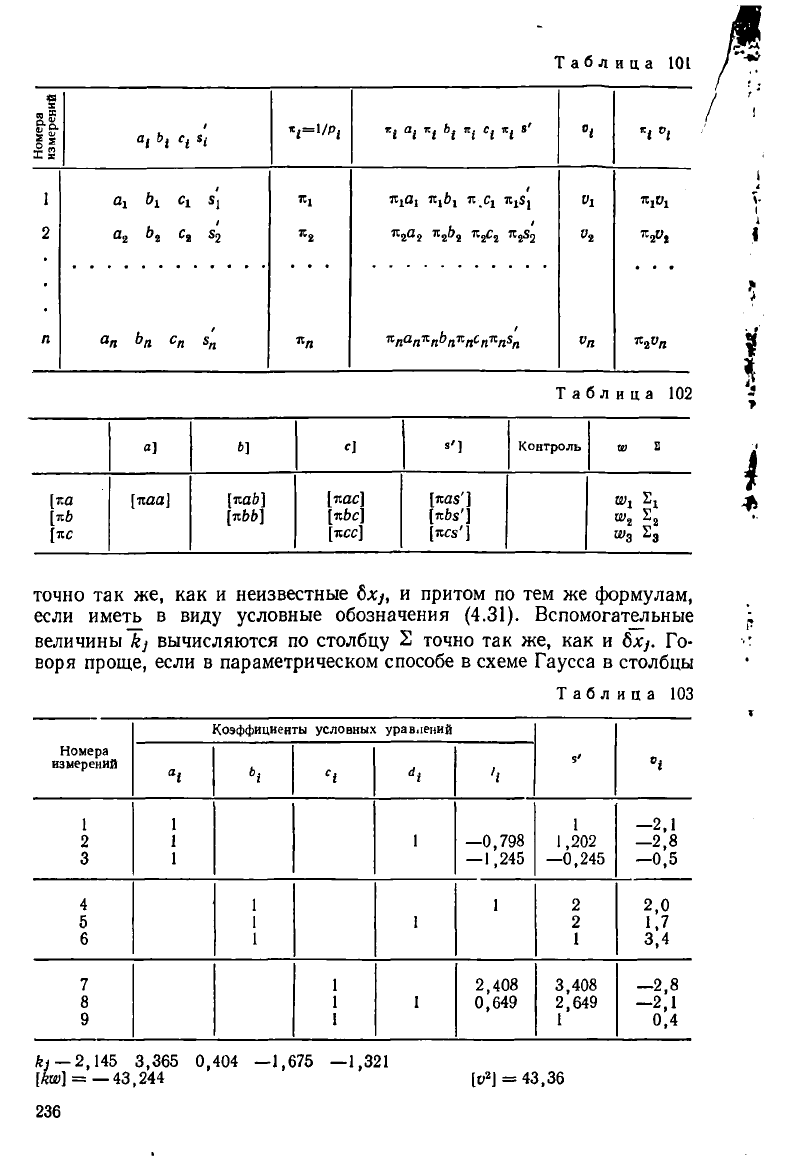
Таблица 81 Таблица 83

Номера

измерений

а, Ь

=1 /р

1 "1

1 *1

"1 "1

1 Й! &1

С1

"Л

Сг

«2

г.

«г

п с

«л

«г^л

Таблица 102

а]

ь1 с]

»'1

Контроль

а) Е

[па [иаа]

[яаЬ]

[нас]

[яа«']

щ 2

[пЬ

[иаа]

[яЬб]

[тсбс] [пЬз']

[тсс

[яЬб]

[нее]

[*«']

точно так же, как и неизвестные Ьх

, и притом по тем же формулам,

если иметь в виду условные обозначения (4.31). Вспомогательные

величины к) вычисляются по столбцу 2 точно так же, как и Ьх

}

. Го-

воря проще, если в параметрическом способе в схеме Гаусса в столбцы

Таблица 103

Коэффициенты условных уравнений

Номера

измерений

°1

1 —0,798

— 1,245

1,202

—0,245

—2,1

—2,8

—0,5

1 2

2,0

1,7

3,4

2,408

0,649

3,408

2,649

-2,8

-2,1

0,4

— 2,145 3,365 0,404 —1,675 —1,321

[кш\ = — 43,244 [ V

] = 43,36

236

Таблица 81 Таблица 83

с]

5']

Контроль О)

[О

[Ь

[с

3 0

—2,043

3,057

—0,149

9,406

1,957

5,000

7,057

5,851

11,271

1,957

5,000

7,057

5,851

11,271

I =

5.4

-7,1

4.5

3,2

9,2

7,357

—2,100

11,557

9,051

14,471

I и 5 поместить числа из столбцов до и 2, то вычисления будут выпол-

няться точно так же и по тем же формулам, что и в параметрическом

способе.

В случае неравноточных измерений схема составления нормальных

уравнений состоит из табл. 101 и табл. 102 (здесь для сокращения за-

писей принято г = 3).

Решение нормальных уравнений выполняется так же, как и в слу-

чае равноточных измерений.

4.9. Составить и решить нормальные уравнения коррелат, вычислить по-

правки углов в задаче 4.5.

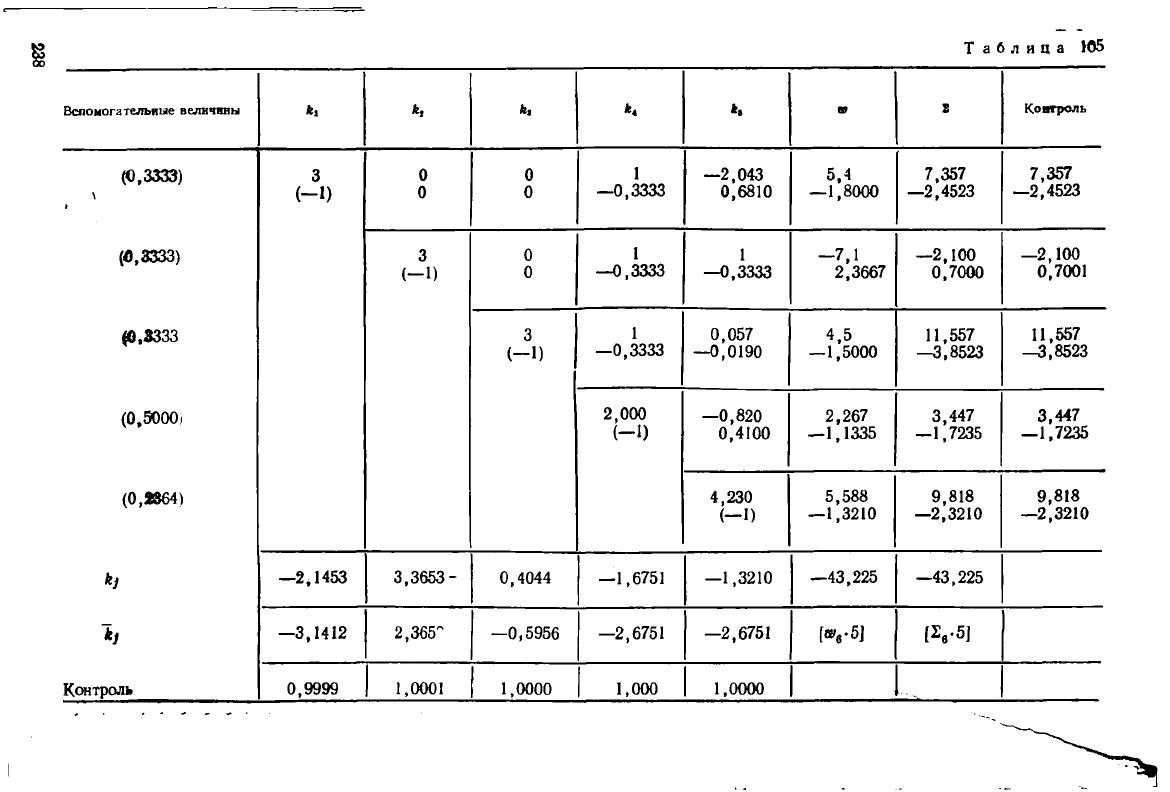
Решение. Составление и решение нормальных уравнений выполнено в

табл. 103—105.

Поправки вычисленные по формуле (4.20), приведены в последней графе

табл. 103. Для удобства их вычисления в последней строке этой таблицы выписа-

ны вычисленные коррелаты.

Как видно, величины поправок совпали с их значениями, полученными в

задаче 3.38 параметрическим способом, что говорит о правильности выполненных

вычислений. По этой причине в этой задаче опущены окончательные контроли

вычислений, присущие коррелатному способу уравнивания.

§ 40. ПОДСЧЕТ ДОПУСТИМОСТИ НЕВЯЗОК УСЛОВНЫХ

УРАВНЕНИЙ

Коррелатный способ по сравнению с параметрическим обладает

тем достоинством, что позволяет попутно с выполнением уравнивания

обнаружить присутствие превосходящих допуски ошибок измерений

путем вычисления значений допустимых невязок. Для этого перепишем

выражение (4.17) в матричной форме

Я( — Д) + 1Г = 0, (4.36)

откуда следует

«7 = В А. (4.37)

Так как коррелатная матрица вектора истинных ошибок измере-

ний, как и самих измерений,

к* = ^Г

где Р'

— матрица обратных весов измерений, а

— дисперсия еди-

237

Таблица

105

Вспомогательные величины

к,

*4 к.

Контроль

(0,3333)

(-1)

—0,3333

—2,043

0,6810

5,4

—1,8000

7,357

—2,4523

7,357

—2,4523

(0,3333)

(-1)

—0,3333

-7,1

2,3667

—2,100

0,7000

—2,100

0,7001

(0,3333

(-1)

—0,3333

0,057

—0,0190

4,5

—1,5000

11,557

—3,8523

11,557

—3,8523

(0,9000)

2,000

(-1)

—0,820

0,4100

2,267

—1,1335

3,447

—1,7235

3,447

—1,7235

(0,1864)

4,230

(-1)

5,588

—1,3210

9,818

—2,3210

9,818

—2,3210

к}

—2,1453 3,3653- 0,4044

—1,6751 —1,3210

—43,225

—3,1412 2,365"

—0,5956

—2,6751

К-5]

[2.-5]

Контроль

0,9999

1,0001

1,0000

1,000

1,0000

ницы-веса, то, применяя обобщенную теорему оценки точности (см.

§ 15), получим для функции (4.36)

= а\ВР'

или с учетом (4.25')

К„ = о2лГ; (4.38)

иными словами, корреляционная матрица невязок равна матрице

коэффициентов нормальных уравнений, умноженной на дисперсию

единицы веса. Из определения корреляционной матрицы следует,

что ее диагональные элементы

о», = о1 \ъаа\,

<4, = 6$, [кЬЬ\,

°1>

= я]

представляют собой дисперсии невязок. Так как измерения, как пра-

вило, подчиняются нормальному закону распределения, то можно

построить доверительные интервалы для математических ожиданий

невязок

и>] — 1ои>) < ЛЦ < и>

}

+ (а^ . (4.40)

При отсутствии систематических ошибок величины Ми// = 0 (так

как из формулы (4.37) М

= ВМ\ = 0, если М

= 0). Тогда из фор-

мулы (4.40) следует

I ^ I <

*»«,,

или (и>Д.оп = ±. (4.41)

где определяется согласно уравнениям (4.39).

Напомним, что коэффициент I выбирается равным 2; 2,5 или 3,

что соответствует вероятности 0,95; 0,987; 0,997.

Отметим, что для решения поставленной задачи необходимо знать

величину о

или а (при равноточных измерениях), в качестве которых

можно принять средние квадратические ошибки, если они получены

надежно, например при предварительной обработке измерений или

из предыдущего опыта измерений.

4.10. Доказать, что в параметрическом способе уравнивания корреляцион-

ная матрица свободных членов нормальных уравнений Я Ах +6 = 0 имеет вид

Кь — °о

н0 на

йти допустимые свободные члены не удается.

4.11. Проверить допустимость невязок условных уравнений в задаче 4.9,

приняв а = 3" и I = 2.

Решение. Для полученных в этой задаче пяти невязок согласно выраже-

ниям (4.39) и (4.41) имеем

Мдоп = Юдоп = (а>з)доп = Мдоп = 2-3 УТ = 10,4";

(ю»)доп = 2-3 У[Щ~ = 6 /9Х = 18.

Как видно, все невязки допустимы.

239.

Таблица 81 Таблица 83

Номера

«1

•

Номера

л»

Л»

п,

вариантов

«1

"г

•

вариантов

л»

Л»

п,

5 6

6 3 3 3

7 7 9

8 4

9 10 5

5 /

8 9

10 12

7 /

4.12. Проверить допустимость невязки га = 70 мм нивелирного полигона,

состоящего из трех ходов с весами Р{ = 1где = 5 км, = 1 км, =»

= 10 км, если среднее квадратическое отклонение на 1 км хода а

= 5 мм, а

I ~ 2.

Решение. Квадратичный коэффициент нормального уравнения, соот-

ветствующего этому полигону, будет я

+ л

+ я

= Ц + + /,

= 22.

Допустимая невязка (ш)

ДО

п = 2 • 5|Л22 ж 50 мм.

Ответ. Невязка недопустима.

4.13. Определить допустимые угловые невязки полигона полигонометриче-

ской сети, состоящего из трех ходов с числом вершин п

(

, по одному из следую-

щих вариантов (табл. 106), если каждый угол измерен с точностью о = 3", а

I •= 2,5.

4.14. Определить допустимость невязок ы>

и ш

условных уравнений коор-

динат в полигонах светодальномерной полигонометрической сети, если при со-

ставлении нормальных уравнений в качестве а

была принята величина

= 0,02 м, а / «= 2. Необходимые данные приведены ниже.

Невязки, м Квадратичные Невязки, ы Квадратичные

коэффициенты Nц коэффициенты Nц

0,090 9,90 —0,260 9,33

—0,010 10,00 +0,090 9,61

—0,150 36,09

§ 41. ОЦЕНКА ТОЧНОСТИ ФУНКЦИЙ В КОРРЕЛАТНОМ СПОСОБЕ

УРАВНИВАНИЯ

Пусть в процессе уравнивания требуется оценить точность функ-

ции

Р = Р(У1 >Уг. Уп). (4.42)

где у

= у

+ VI — уравненные результаты измерений. Приводя

функцию (4.42) к линейному виду путем разложения в ряд Тейлора,

получим

^ = 2 Пщ, (4.43)

11=1

где обозначено /

= Р(у

{

, у

, ..., у

дР

дУ1

• (4-44)

240

В теории коррелатного способа доказывается, что обратный вес

уравненной функции выражается в виде алгоритма Гаусса

1 11

{паа]

[ъЫ.Ц

причем

ЫП = (4-46)

естк обратный вес функции, вычисленной по неуравненным измере-

ниям. Если алгоритм (4.45) не зависит от того, как выбрана функция,

т. е. по каким измерениям она вычислена, то для выражения (4.46)

будем получать различные значения в зависимости от выбора измере-

ний. Например, для обратного веса уравненной отметки репера 1

нивелирной сети (см. рис. 62) получим одно и то же значение, если

вычислить ее от отметок марок /, //, III и IV, тогда как формула

(4.46) даст различные значения. Заметим также, что всегда

< '

р*

где

Для контроля вычисления применяется формула

—!— = [ф . Г] = [./5]

[7ШЛ

- •

Р ^ [тсаа] [пбб •

]

[*уМ'-0П«Д»- ('-'))

Ые • (

— 01

[та^ = [тс аа] +

Гтсаб]

+ ... + Ка^] + [«а/],

[лбе] = [ъаЬ] + [кЬЬ] + ... + + 1кЦ),

[тг§5] = + [тг Ьв] + • • • + [тс^] +

«1 = «I + к = Щ + Ь

+ ••• + /х»

®2 = 4 + /г =

2 + + • • • +^2 + /г»

= < + /п = а

+ Ь

н !-«» + /„.

(4.47)

Как видно, в коррелатном способе суммы (4.47) отличаются от

(3.29) тем, что вместо свободных членов /

в них фигурируют коэффи-

циенты функции С учетом этого схемы для составления нормаль-

ных уравнений имеют тот же вид, что и в параметрическом способе

уравнивания, однако с той разницей, что столбец / заменяется столб-

цом Д а столбец коэффициентов функций — столбцом невязок до.

241.

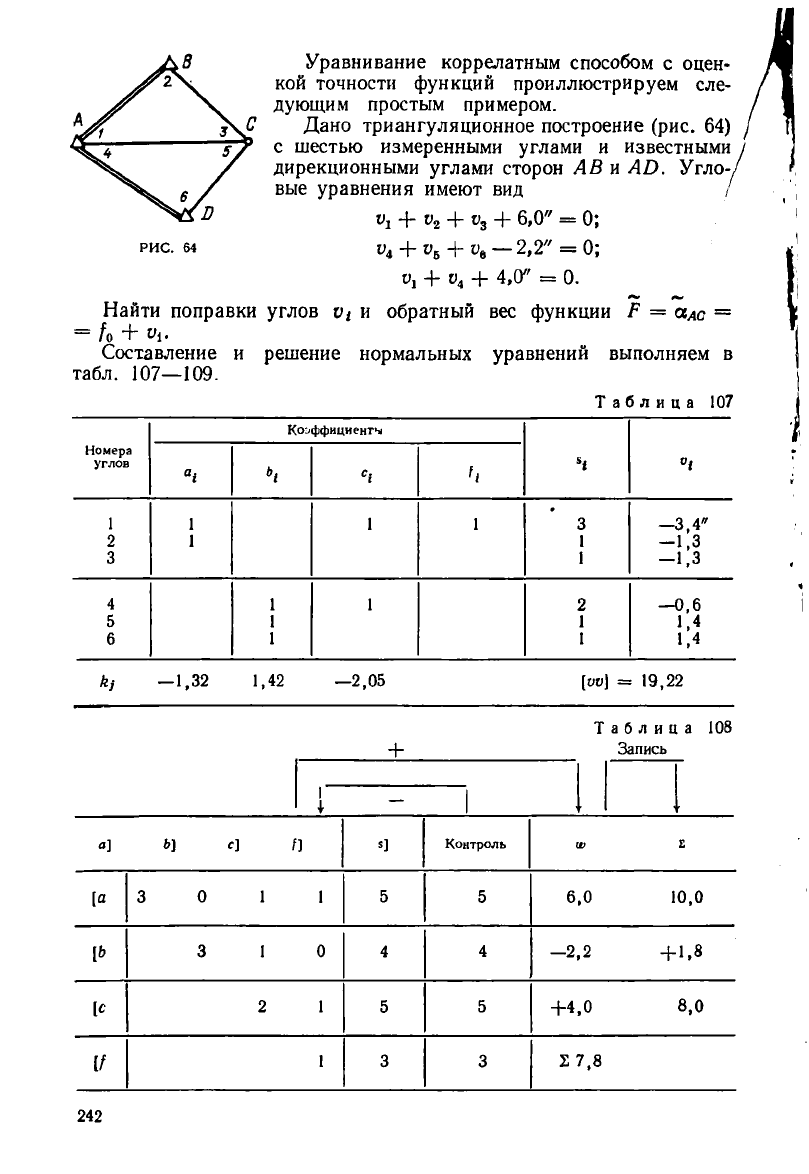
Уравнивание коррелатным способом с оцен-

кой точности функций проиллюстрируем сле-

дующим простым примером.

.С Дано триангуляционное построение (рис. 64)

с шестью измеренными углами и известными

дирекционными углами сторон А В и АО. Угло-/

у вые уравнения имеют вид /

я V

+ V

+ 6,0" = 0;

РИС. 64 У

+ У

+ о

— 2,2" = 0;

+ V

+ 4,0" = 0.

Найти поправки углов VI и обратный вес функции Р = аас =

= /о +

Составление и решение нормальных уравнений выполняем в

табл. 107—109.

Таблица 107

Коэффициент»»

Номера

углов

1 1 3

—3,4"

-1,3

1 2

—0,6

1,4

к}

—1,32 1,42 —2,05

м =

19,22

Таблица 108

Запись

а]

Ь] с] /) 5]

Контроль

ш Е

3 0 11 5

5 6,0 10,0

[Ь

3 I 0 4

-2,2

+ 1.8

[С

2 1

+4,0

8,0

3 3

2 7,8

242.

В табл. 108 и 109 стрелками показан порядок выполнения конт-

ролеЙ. Так, в табл. 108 для того, чтобы получить столбец 2, необхо-

димо в каждой строке из чисел столбца «контроль» вычесть числа столб-

ца/и прибавить числа столбца невязок т.

Контролем решения этой задачи являются равенства

+ Щ + у

= — щ = — 6,0;

«4 + + Ч = — Щ = 2,2;

Щ + = — = —

»°

и соотношение [от] = —

Для вычисления средней квадратической ошибки уравненной

функции применяем формулу

т~ = т I/ 1 /Р~ .

р г р

Обратный вес функции в решенной задаче получен равным

1/Р~ = 0,329, (4.48)

а средние квадратические ошибки

от = У 19,22/3 = 2,5"; = 2,5 }/0,329 = 1,4"

(следует, однако, иметь в виду, что их значения ненадежны из-за

малого числа избыточных измерений г = 3).

В случае необходимости в схеме Гаусса можно найти обратные

веса сразу нескольких функций (см. задачу 3.48).

В заключение приведем матричную форму

/Р„ = [Р-^Г — !Р-

• ЛГ"

• ВР^р (4.49)

для вычисления обратного веса функции, где матрица / =•= Шг---!п)

(остальные матрицы были объяснены ранее).

Для случая равноточных измерений

1 /Р„ = (Г — (4.50)

Матрица Ы'

может быть получена в схеме Гаусса точно так же,

как и матрица весовых коэффициентов <2 в параметрическом способе.

Так, в рассмотренном примере эта матрица

/ 0,416 0,083 — 0,250\

ЛГ1 =1 0,083 0,416 —0,250).

\—0,250 —0,250 0,752/

Поскольку матрицы

/1 1 1 0 0 0\

0 0 0 111,

\1 0 0 10 0/

/ = (1 0 0 0 0 0 0),

243.