Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Таблица 64

Номера

сторон

д*

д»

Ду

Ах

—1189,756

623,363

—121,033

—897,670

629,968

—1393,245

—94,875

—1488,120

—2980,333

1,1710342

—2,235046

0,0623754

1,6577584

—4,7309276

49°30'16,0"

294 06 16,6

3 34 09,2

238 54 02,2

281 56 06,8

Матрица

/? =

2,263 — 0,058

2,661

— 0,007 + 0,113

+ 0,113 —1,822

1,482 — 0,645

2,219

Вектор свободных членов

= АЧ =

1,150'

— 3,973

0,926

7,060,

Юз.

Такой же результат получается по обычной схеме составления нормальных

уравнений.

Векторы неизвестных и поправок

Д* = 10"

'0,271

2,683

3,139

6,283.

Уравненные неизвестные представлены ниже

Пункт *

623,363

—897,670

—1393,245

—1488,120

а окончательный контроль — в табл. 64.

Как видим, вычисленные по уравненным координатам дирекционные углы

совпали в пределах точности вычислений с уравненными дирекционными углами,

приведенными в табл 60.

В этой задаче, очевидно, матрица / совпадает с матрицей /, полученной в

предыдущей задаче, так как оцениваются те же функции 5

и а

. По упомянутой

выше программе получена матрица

г'0,443 •0,0181 —0,015 —0,042'

0,971 0,313 0,890

0,874 0,513

1,333

ю-

184

_/ 0,458- Ю-

—0,340- 10"

—0,900- Ю"

—0,581 • 10~П

^"1—0,006 • Ю-

+ 0,137 • 10"* — 0,195 • 10"

—0,551 • 10"

/ '

С,=

/д/Т =

(

371

О.*» 10-П

* \0,232 • Ю

-2

0,912 }

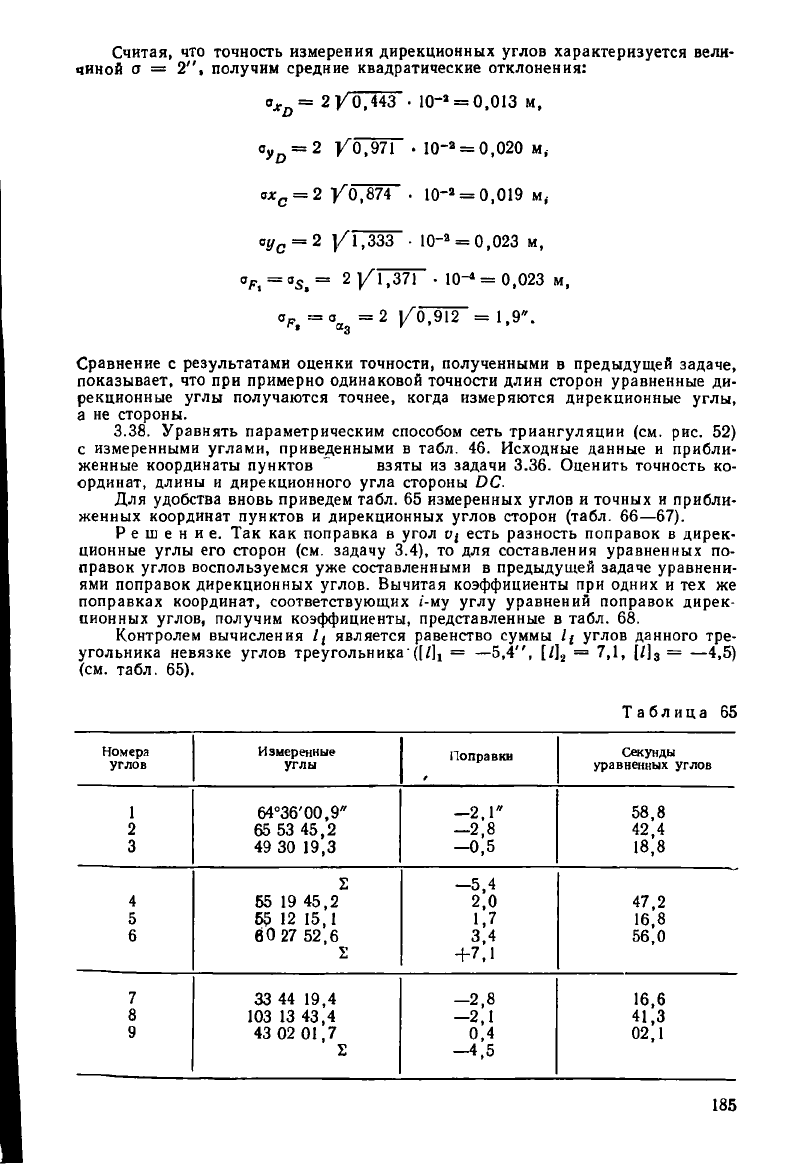
Считая, что точность измерения дирекционных углов характеризуется вели-

чиной а = 2", получим средние квадратические отклонения:

Хо

= 2 У 0,443 • Ю~

= 0,013 м,

0у

= 2 УО^ШГ • Ю-

= 0,020 м,

чх

= 2 У0^Ш~ . 10"

= 0,019 м,

оу

= 2 }/1,333 • 10-

= 0,023 м,

= =

371

10-4

= °.°

23 м

V, = =

КМГ2"= 1,9'.

Сравнение с результатами оценки точности, полученными в предыдущей задаче,

показывает, что при примерно одинаковой точности длин сторон уравненные ди-

рекционные углы получаются точнее, когда измеряются дирекционные углы,

а не стороны.

3.38. Уравнять параметрическим способом сеть триангуляции (см. рис. 52)

с измеренными углами, приведенными в табл. 46. Исходные данные и прибли-

женные координаты пунктов ~ взяты из задачи 3.36. Оценить точность ко-

ординат, длины и дирекционного угла стороны ОС.

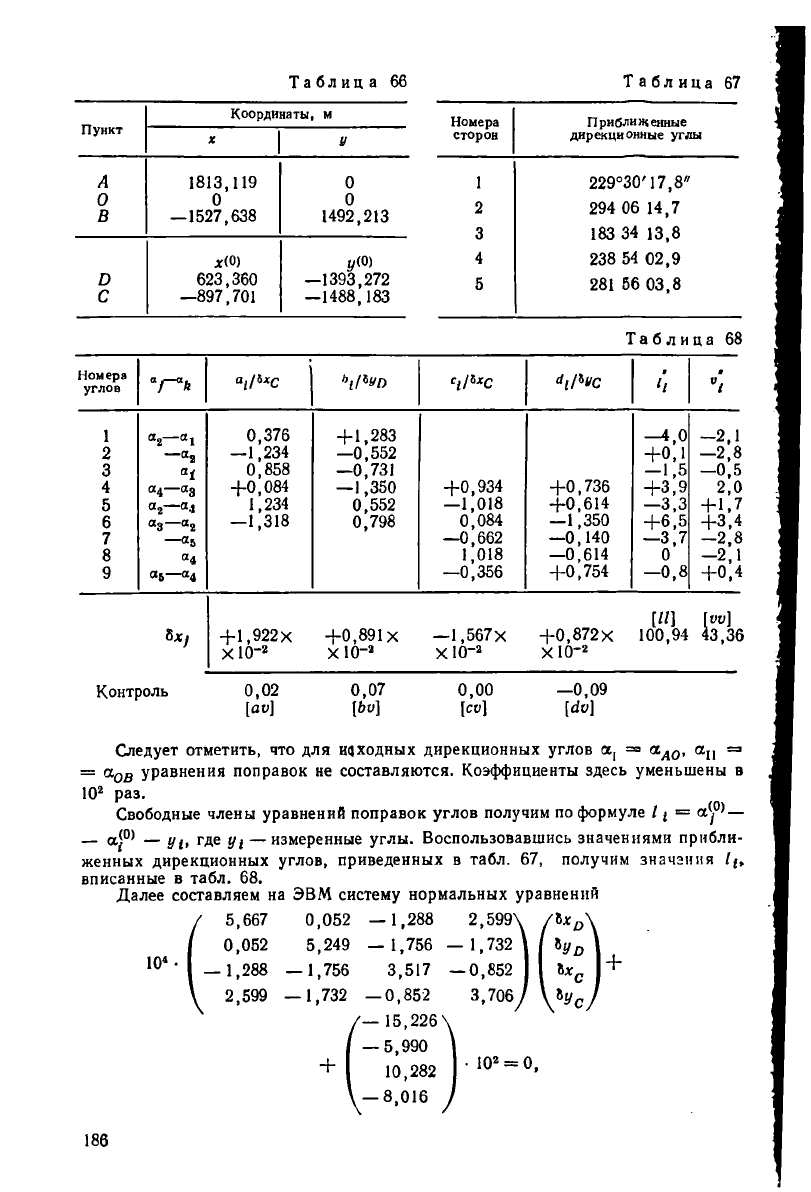
Для удобства вновь приведем табл. 65 измеренных углов и точных и прибли-

женных координат пунктов и дирекционных углов сторон (табл. 66—67).

Решение. Так как поправка в угол есть разность поправок в дирек-

ционные углы его сторон (см. задачу 3.4), то для составления уравненных по-

правок углов воспользуемся уже составленными в предыдущей задаче уравнени-

ями поправок дирекционных углов. Вычитая коэффициенты при одних и тех же

поправках координат, соответствующих 1-му углу уравнений поправок дирек-

ционных углов, получим коэффициенты, представленные в табл. 68.

Контролем вычисления Ц является равенство суммы углов данного тре-

угольника невязке углов треугольника'([/]

= —5,4", [/]

= 7,1, [/]

= —4,5)

(см. табл. 65).

Таблица 65

Номера

углов

Измеренные

углы

Поправки

Секунды

уравненных углов

64°36'00,9"

65 53 45,2

49 30 19,3

—2,1"

-2,8

-0,5

58,8

42,4

18,8

55 19 45,2

55 12 15,1

6 0 27 52,6

—5,4

2.0

1,7

3,4

+7,1

47,2

16,8

56,0

33 44 19,4

103 13 43,4

43 02 01,7

-2,8

-2,1

0,4

—4,5

16,6

41,3

02,1

185.

Таблиц а 66

Таблица 67

Пункт

Координаты, м Ном,™

Приближенные

дирекционные углы

Пункт

X | у сторон

Приближенные

дирекционные углы

1813,119

— 1527,638

0 1

1492,213 *

229°30'17,8"

294 06 14,7

183 34 13,8

238 54 02,9

281 56 03,8

*<0)

623,360

—897,701

1/(0) 4

—1393,272 к

-1488,183

229°30'17,8"

294 06 14,7

183 34 13,8

238 54 02,9

281 56 03,8

Таблица 68

Номера

углов

а,/

8х

Ь^Ьур

{

/Ъх

/ьи

* а

—а,

0,376 +1,283

-4,0

-2,1

—=2

—1,234

—0,552

+0,1

-2,8

0,858

—0,731 —1,5 -0,5

4 а

—а

+0,084

—1,350

+0,934

+0,736 +3,9

2,0

—

1,234

0,552

—1,018

+0,614

-3,3

+1.7

3—

—1,318

0,798

0,084 —1,350

+6,5

+3,4

—а

—1,318

0,798

—0,662 —0,140

-3,7

-2,8

1,018

—0,614

-2,1

—а

—0,356

+0,754 -0,8 +0,4

+1.922Х

X Ю

-2

+0,891 х

X Ю

-2

—1.567Х

X Ю

-2

+0.872Х

Х10-

[Щ

100,94

Гго]

43,36

Контроль 0,02 0,07 0,00 —0,09

[аь] [Ьо] [со]

Следует отметить, что для исходных дирекционных углов а, = а

А0

, а

=•

= а

ов

уравнения поправок не составляются. Коэффициенты здесь уменьшены в

раз.

Свободные члены уравнений поправок углов получим по формуле 1^ = а

(

—

— а|

— У1, где У1 — измеренные углы. Воспользовавшись значениями прибли-

женных дирекционных углов, приведенных в табл. 67, получим значзния 1

(

вписанные в табл. 68.

Далее составляем на ЭВМ систему нормальных уравнений

5,667 0,052 — 1,288 2,599\

0,052 5,249 — 1,756 —1,732

' 1 — 1,288 — 1,756 3,517 —0,852

2,599 — 1,732 — 0,852 3,706

15,226

— 5,990

10,282 1-

102

= °.

, —8,016

186.

получаем обратную матрицу

0,287 — 0,077 0,010 — 0,235^

— 0,077 0,349 0,210 0,266

С==

1 0,010 0,210 0,440 0,193 I '

10_4

у—0,235 0,266 0,193 0,604

вектор неизвестных поправок

В табл. 68 вычисляем поправки и выполняем контроль [аа] = [М =

•= [а>] = [А>] = 0.

Окончательный контроль решения задачи выполняется путем вычисления

' по уравненным координатам, приведенным ниже, сначала дирекционных углов

сторон, а по ним — углов. Последние должны совпадать с их значениями, при-

веденными в табл. 65. Этот процесс здесь опущен, тем более что задача будет

решена коррелатным способом в главе 4.

Пункт * у

О 623,379 —1393.263

С —897,717 —1488,174

Оценка точности. В рассматриваемой сети число избыточных изме-

рений достаточно, чтобы можно было вычислить среднюю квадратическую ошиб-

ку измерения одного угла

[то] Аз, 36

5 =У

Средние квадратические ошибки уравненных координат:

= 2,9/0,287 • 10"

= 0,016 м,

Уо

= 2,9 /М49~ • 10~

= 0,017 м,

"о

хс

= 2,9 /0,440 • 10"

= 0,019 м,

= 2,9 /67604" • Ю-

= 0,023 м.

Для оцениваемых функций, как и в предыдущих задачах, находим

/0,286-Ю"

—0,281 • 10"

— 0,428- 10"

— 0,448 . Ю"

]

~ \0,190 • Ю

-2

0,136- Ю-

0,059- 10"

—0,420 )'

/0,723 • Ю

-4

0,165 • Ю"

~ \0,164 • 10"

0,740 Г

Средние квадратические ошибки:

= 2,9 /о,723 • 10"

= 0,025 м,

«, = 2,9/0,740 = 2,5".

187.

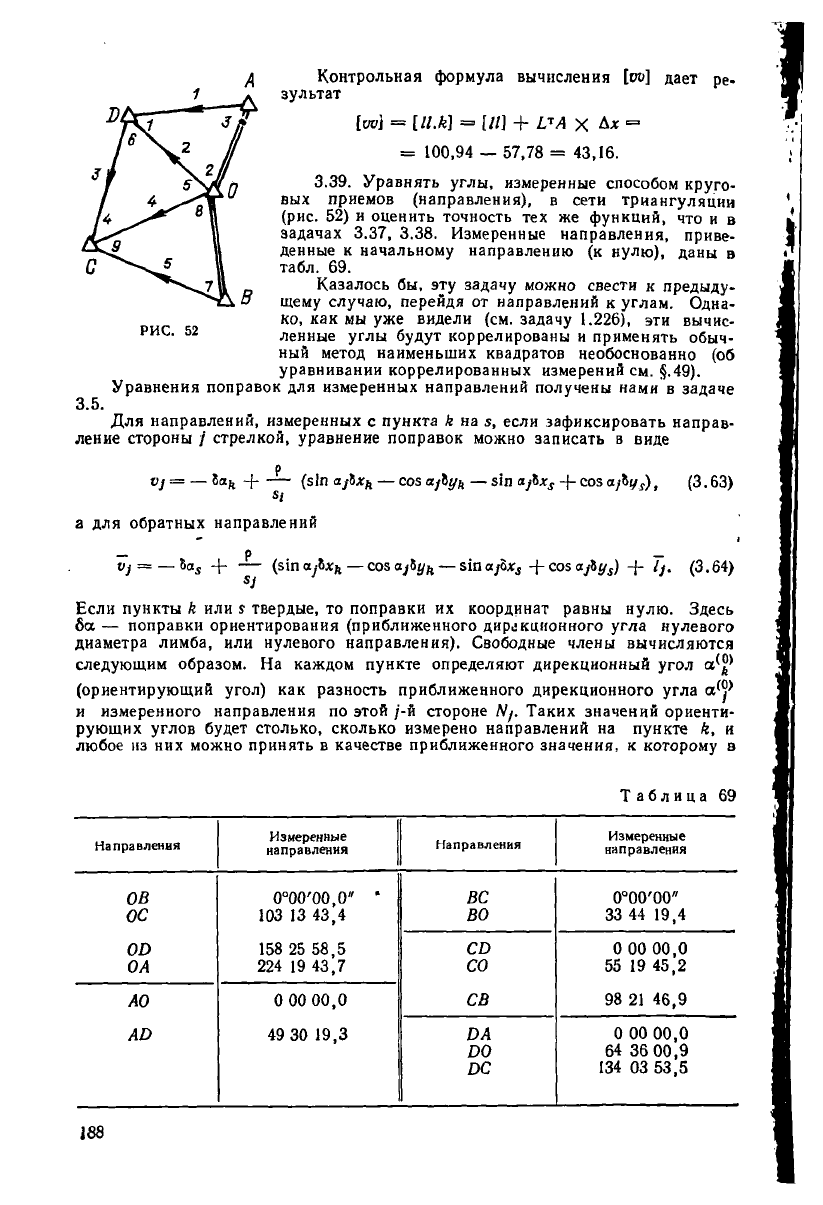
^ Контрольная формула вычисления [со] дает ре-

зультат

[Ы = [Ц.к] = [//] + X А* =

= 100,94 — 57,78 = 43,16.

3.39. Уравнять углы, измеренные способом круго-

вых приемов (направления), в сети триангуляции

(рис. 52) и оценить точность тех же функций, что и в

задачах 3.37, 3.38. Измеренные направления, приве-

денные к начальному направлению (к нулю), даны в

табл. 69.

Казалось бы, эту задачу можно свести к предыду-

щему случаю, перейдя от направлений к углам. Одна-

ко, как мы уже видели (см. задачу 1.226), эти вычис-

ленные углы будут коррелированы и применять обыч-

ный метод наименьших квадратов необоснованно (об

уравнивании коррелированных измерений см. §.49).

Уравнения поправок для измеренных направлений получены нами в задаче

3.5.

Для направлений, измеренных с пункта к на 5, если зафиксировать направ-

ление стороны / стрелкой, уравнение поправок можно записать в виде

V] = — Ьа

+ (з

!л

а— соз аАуь — 51п

Лх

-{- соз

Лу

(3.63)

а для обратных направлений

— Р —

V) = — + — (зш — соз а)Ьу

— 5Ш а-(- С05

<х]Ъу

)

-{- /у. (3.64)

Если пункты к или у твердые, то поправки их координат равны нулю. Здесь

8а — поправки ориентирования (приближенного дир^кционного угла нулевого

диаметра лимба, или нулевого направления). Свободные члены вычисляются

следующим образом. На каждом пункте определяют дирекционный угол

(ориентирующий угол) как разность приближенного дирекционного угла а'^

и измеренного направления по этой /-й стороне N1. Таких значений ориенти-

рующих углов будет столько, сколько измерено направлений на пункте к, и

любое из них можно принять в качестве приближенного значения, к которому а

Таблица 69

Направления

Измеренные

направления

Направления

Измеренные

направления

ов

ОС

0°00'00,0" •

103 13 43,4

ВС

во

0°00'00"

33 44 19,4

Ой

ОА

158 25 58,5

224 19 43,7

СИ

СО

0 00 00,0

55 19 45,2

АО

0 00 00,0

св

98 21 46,9

Ай 49 30 19,3

сл

оо

ОС

0 00 00,0

64 36 00,9

134 03 53,5

188.

результате уравнивания и будет определена поправка 6а. Но с целью удобства

вычислений в качестве приближенного значения а

<0)

берут среднее из значений,

полученных по всем направлениям.

Таким образом, на каждом пункте к для направления /

Контроль: ^ I] = 0.

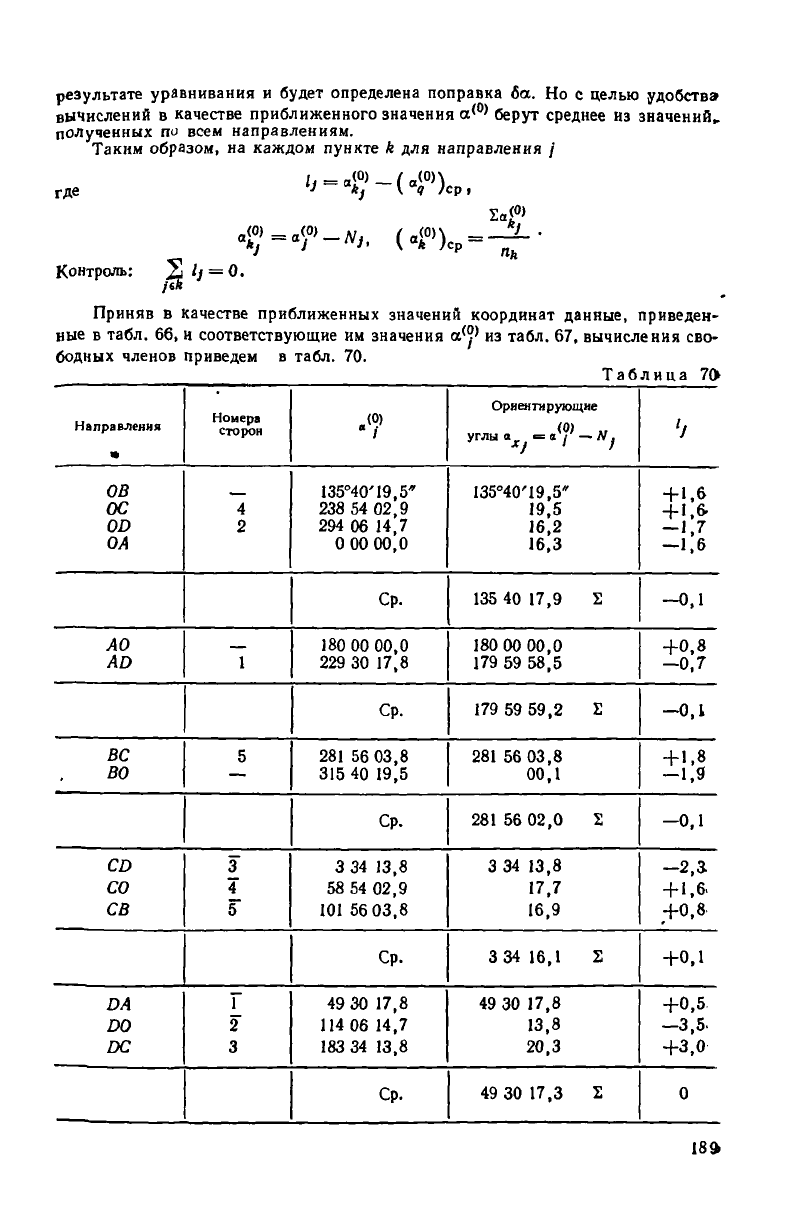
Приняв в качестве приближенных значений координат данные, приведен-

ные в табл. 66, и соответствующие им значения а

(

?' из табл. 67, вычисления сво-

бодных членов приведем в табл. 70.

Таблица 70

Направления

•

Номера

сторон

Ориентирующие

(0)

углы а =« / — N!

ОВ

ОС

ОИ

ОА

135°40'19,5*

238 54 02,9

294 06 14,7

0 00 00,0

135°40'19,5*

19,5

16,2

16,3

+ 1.6

+1,6-

-1.7

-1,6

Ср.

135 40 17,9 X

—0,1

АО

Ай 1

180 00 00,0

229 30 17,8

180 00 00,0

179 59 58,5

+0,8

-0,7

Ср.

179 59 59,2 Е

-0,1

ВС

ВО

281 56 03,8

315 40 19,5

281 56 03,8

00,1

+1.8

—1,9

Ср.

281 56 02,0 X

-0,1

СО

3 34 13,8

—2,3.

СО

58 54 02,9

17,7

+ 1.&

СВ

101 56 03,8

16,9 +0,8

Ср. 3 34 16,1 2

+0,1

ОА

49 30 17,8 49 30 17,8

+0,5

цо

114 06 14,7

13,8

-3,5.

йС

183 34 13,8

20,3

+3,0

Ср.

49 30 17,3 2 0

18»

Учитывая, что решаемая и предыдущая задачи имеют одни и те же цифровые

данные, можно показать, что свободные члены уравнений поправок углов (см.

табл. 68) должны быть равны разностям свободных членов Ц уравнений попра-

вок направлений, образующих 1-й угол. Действительно,

'^'ш-'о^-

'^-

= = - 0,7-0.8=-!,5",

ОО ОЛ

ОА ~~ 'оо

'АО~

АО'

/4 = / _ — /= —1,6 + 2,3 = 3,9",

со со

ос

~ '>

7 —

1,6 = —3,3",

/. =

— / =3,0 + 3,5 = 6,5",

' ОС оо

= '„ — / „ _ = — 1,9 — 1,8 = — 3,7",

ВО ВС ' ' ' '

/ = / _ / =1,6—1,6 = 0,

" ОС ОВ ' ' '

/, = /-/ =0,8 —1,6= —0,8".

св со ' ' '

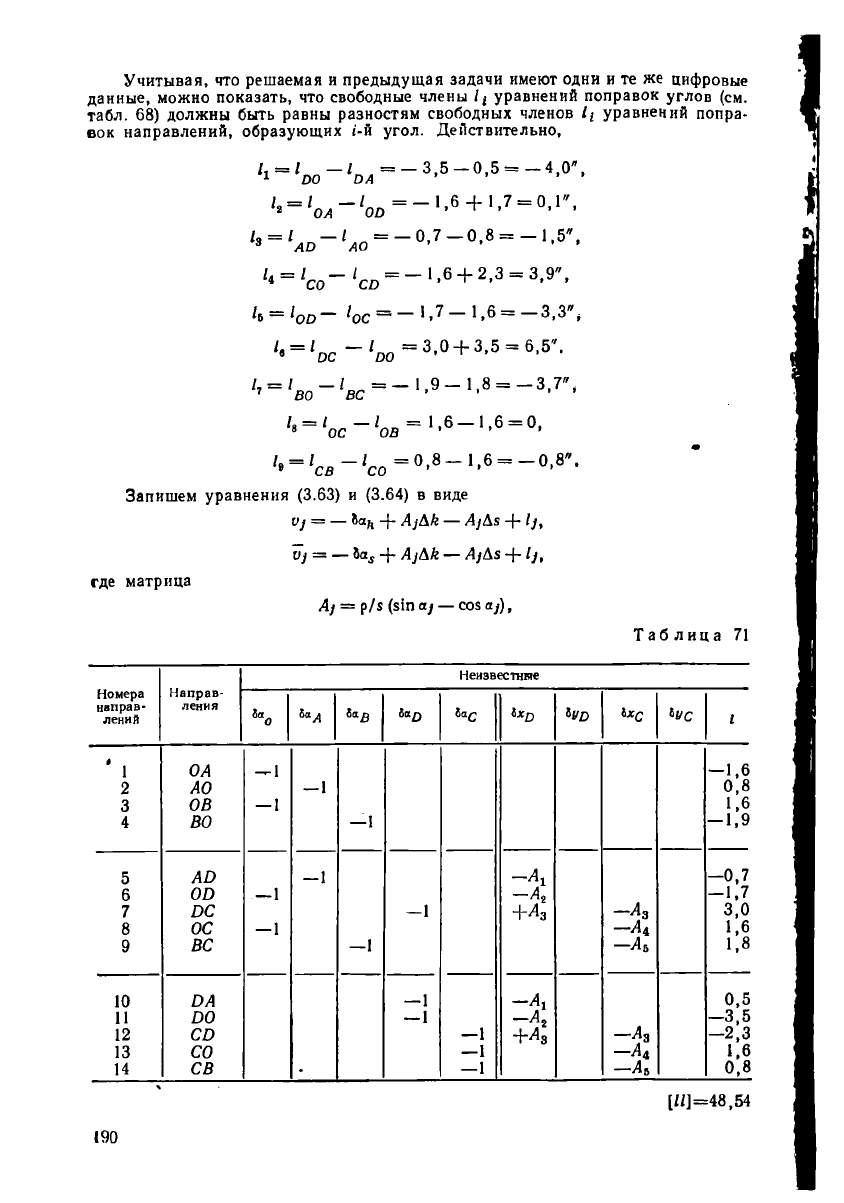
Запишем уравнения (3.63) и (3.64) в виде

V] = — + А]ИК — Д1Д5 + I),

= — 8а, + А]&к — А]Аз + I],

где матрица

Лу

—

р/5 (з!п а] — соз а]),

Таблица 71

Номера

неправ*

лений

Направ-

ления

Неизвестнне

Номера

неправ*

лений

Направ-

ления

»о

5а

Ьл

8ад 8а

Ьх

'(/О

ЬУС

ОА

АО

ОВ

ВО

— 1

—1

—1,6

0,8

1,6

-1,9

ЛО

ОЙ

ОС

ВС

— 1

—1

-1

-А,

+А

-А,

—А

-А

-0,7

-1.7

3,0

1,6

1,8

ЙА

ОО

СО

СВ

—1

-А

—л

+А

-А

А 4

АЪ

0,5

-3,5

-2,3

1,6

0,8

[»]=48,54

(90

векторы

"-Ю- -с;;)-

'Для нашей сети уравнения поправок представим в табл. 71. С ее помощью

составим систему нормальных уравнений, матрицу коэффициентов которых за-

пишем в блочном виде [7]

При этом легко получаем

Д« =

Видно, что ее диагональные элементы равны числу направлений, измерен-

ных на каждом пункте и расположенных в ней в порядке нумерации пунктов.

Матрица

Л, О

*и-Г ° *

— А

+ А

+ А, А

— Аз +Л

+Л

Блоки ее первых трех строк, относящихся к исходным пунктам, равны мат-

рице Л/, расположенной в столбце, номер которого равен номеру определяемого

пункта, причем / — номер стороны, связывающей пункт с определяемым.

Блоки остальных строк, относящихся к определяемым пунктам и располо-

женным по диагонали, равны 2± А] тех сторон, которые входят в соответству-

ющий определяемый пункт, причем «+» ставится, если сторона направлена к

пункту, «—» — если выходит из него. Недиагональные блоки равны ±Лу той

стороны, которая связывает определяемые пункты, номера которых определяют-

ся пересечением строки и столбца; «+» ставится, если номар строки меньше но-

мера столбца, «—» — в противном случае.

Наконец, как видно из табл. 71, блок /?

2г

= 2/?, а матрица К составляется

точно так же, как при уравнивании сети с измеренными дирекционными углами

(см. задачу 3.37).

Вектор свободных членов представим в виде

причем, как легко убедиться, Ь^ = 0, а вектор Ь

составлен из блоков

(Ь

)=2±ЛТ^, (3.65)

/65

где /.у = I) + /у (сумма свободных членов уравнений поправок прямых и обрат-

ных направлений). Знак «+» ставим, если пункт « — начальная по отношению

к /-й стороне точка, «—» — если конечная.

Так, в нашей задаче

ь==

(— ~

* +

з \

Ц —А

—А

Ц/ '

Составим теперь матрицу Я в численном виде, используя матрицы Л/, уже

полученные в предыдущей задаче.

191.

«11

«й

4 0 0

2 0

0 0

—1,234

—0,856

—0,552

0,731

—1,018

—0,662

+0,614

—0,140

3 0

—2,006

+0,084

4,526

—1,171

—1,350

—0,116

5,322

—0,084

—1,764

—0,014

+0,226

2,964

1,350

1,824

+0,226

—3,664'

—1,290

4,438

Заметим, что коэффициенты матрицы уменьшены в 10' раз, а матрицы

— в 10

. Это равносильно представлению системы нормальных уравнений в

виде

/?„ • 10

'(Д* • 10

-8>

) + /?

• 10

8,+5

'(д

• Ю-'О +

Ь]

• Ю

' =0,

, • 10

8,+8

> • 10

+ /?

2г

• 10

' (Д, • Ю

-5

') + Ь

. 10

> = О,

эквивалентной системе уравнений

К11Л1+Я

+&,=0,

(Л, +Я

г2

+й

= 0.

Здесь Д

— вектор поправок ориентирующих углов, Д

— вектор поправок

координат.

Мы приняли ^ «= 0, з

= —2. Поэтому поправки бс^ и 6х '6у) после решения

системы следует соответственно оставить без изменения и уменьшить в 10

раз.

Свободные члены нормальных уравнений согласно выражению (3.65) полу-

чим с помощью табл. 72.

Таблица 72

Номера

сторон

г.,-1,+1,

1-, = ь ,

1 1 г!

1 —0,856

0,731 .

-0,2

0,171

—0,146

-1,234

-0,552

—5,2

6,417

2,870

—0,084

1,350

0,7

—0,059

0,945

-1,018

0,614

3.2

—3,258

1,965

—0,662

—0,140

2,6

-1,721

—0,364

е виде вектора

(

—6,647 \

— 1,779 \

Г — 2,546/

892.

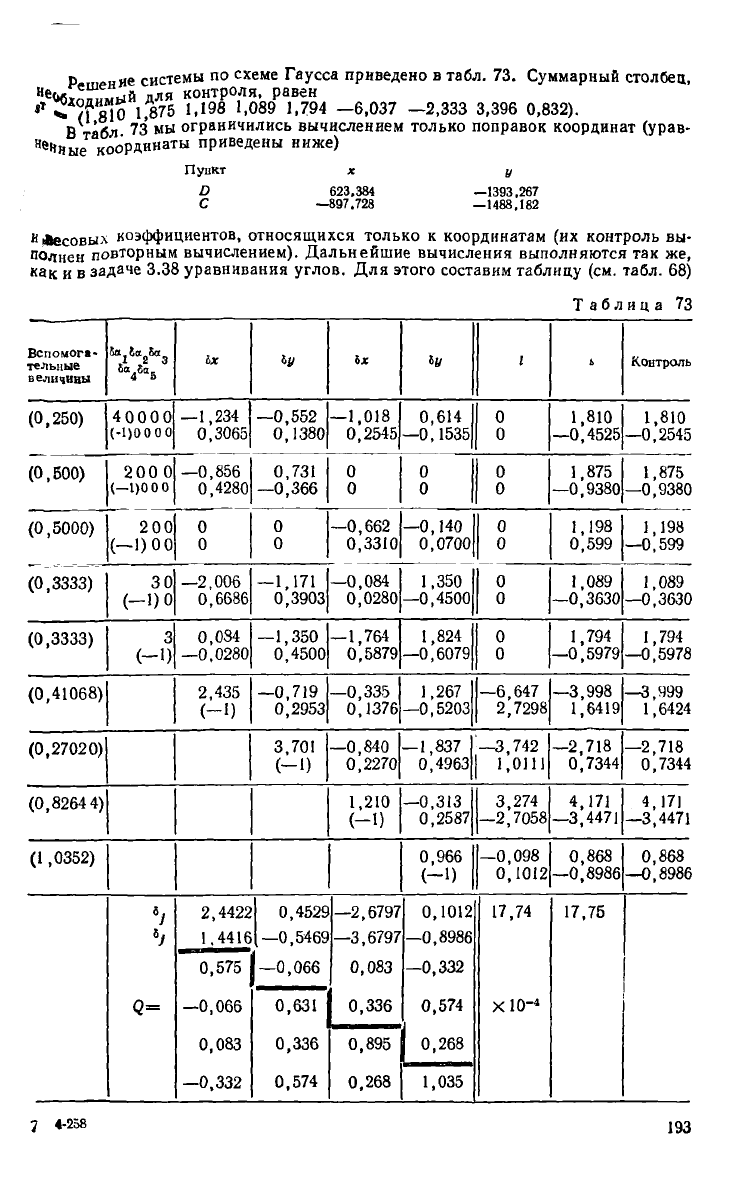
р „няе системы по схеме Гаусса приведено в табл. 73. Суммарный столбец,

Не

мС;!г;;„ый для контроля, равен

П 8\0 1,875 1,198 1,089 1,794 —6,037 —2,333 3,396 0,832).

В табл 73 мы ограничились вычислением только поправок координат (урав-

ненные координаты приведены ниже)

Пункт х у

й 623,384 —1393,267

С —897.728 —1488,182

"Лесовых коэффициентов, относящихся только к координатам (их контроль вы-

полнен повторным вычислением). Дальнейшие вычисления выполняются так же,

как и в задаче 3.38 уравнивания углов. Для этого составим таблицу (см. табл. 68)

Таблица 73

Вспомога-

тельные

величины

Ьх

Ьу

5х

Ьу

1 &

Контроль

(0,250)

40000

(-1)0000

—1,234

0,3065

—0,552

0,1380

—1,018

0,2545

0,614

—0,1535

1,810

—0,4525

1,810

—0,2545

(0,500)

200 0

(—1)0

0 0

—0,856

0,4280

0,731

—0,366

1,875

—0,9380

1,875

—0,9380

(0,5000)

200

(-1)0 0

—0,662

0,3310

—0,140

0,0700

1,198

0,599

1,198

—0,599

(0,3333)

(-1)0

—2,006

0,6686

—1,171

0,3903

—0,084

0,0280

1,350

—0,4500

1,089

—0,3630

1,089

—0,3630

(0,3333)

(-1)

0,034

—0,0280

—1,350

0,4500

—1,764

0,5879

1,824

—0,6079

1,794

—0,5979

1,794

—0,5978

(0,41068)

2,435

(-1)

—0,719

0,2953

—0,335

0,1376

1,267

—0,5203

—6,647

2,7298

—3,998

1,6419

—3,999

1,6424

(0,27020)

3,701

(-1)

—0,840

0,2270

— 1,837

0,4963

—3,742

1,0111

—2,718

0,7344

—2,718

0,7344

(0,8264 4)

1,210

(-1)

—0,313

0,2587

3,274

—2,7058

4,171

—3,4471

4,171

—3,4471

(1,0352)

0,966

(-1)

—0,098

0,1012

0,868

—0,8986

0,868

—0,8986

2,4422

1,4416

0,575

0,4529

—0,5469

—0,066

—2,6797

—3,6797

0,083

0,1012

—0,8986

—0,332

17,74

17,75

а=

—0,066

0,631 0,336

0,574

Х10"

0,083

0,336

0,895

0,268

—0,332

0,574

0,268 1,035

7 4-258

193