Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений
Подождите немного. Документ загружается.


Таблица 29
Варианты
5, м 7, градус
см
Варианты
5, м
7, градус
т^, см
1
120
6
3,0 6 225
9 4,0
2
150
7
3,0
7
100
4
1,0
3 200
5
2,0
8
250 6
4,0
4
140 10 2,0
9
130 3
1,0
5
175
8
3,0
10
240 7
4,0
откуда
т
2
=
2
т„ = •
° 2 соз
2
7 ' 1 2П
2
з'щ
2
•(
Далее
т
5
0,10
- - = 0,072 м;
У 2 соз 7 У
2
соз 10°
0,072 1
й 210 3000
_ тд' о ПО?' _
й
,,
т = = — — = о,о.
7
У 20
51П
у У 2 • 210 • 81П 10°
2.62. Превышение к получено по формуле к = О какой точностью
должно быть измерено расстояние « и угол наклона у, если к требуется получить
со средней квадратической ошибкой т/,?
Значения величин 8, у я т/, даны в табл. 22.
2.63. В государственной геодезической сети 1 класса на концах базисных
сторон определяют азимуты Лапласа А, которые вычисляют по формуле А =•
= а — (А, — /,)51П<р.
Найти, с какой точностью должны быть определены астрономический ази-
мут а, разности долгот (А, — Ь) и широта <р, чтобы азимут был получен не грубее
6,5" при данных ср = 60°, (X — I) => 15".
Ответ: т
а
= 0,29".
Ниже приводится еще ряд задач на оценку точности функций.
2.64. Найти с. к. о. угловой невязки разомкнутого полигонометрическо-
го хода, если с. к. о. измерения одного угла а = 3 а число вершин 10.
Ответ: а
2
= 90.
2.65. Найти то же, если примычные дирекционные углы а
нач
и а
нон
не
безошибочны, а определены с точностью а = а = I".
а
нач "кон
Ответ: <т
2
= 92.
2.66. Написать формулу для определения с. к. о. линии длиной 5 м, если
ее измеряли подвесным мерным прибором со с. к. о. измерения 1 м (коэф-
фициентом случайного влияния), равным а
ш
.
2.67. Углы Р] и ^ треугольника измерены с точностью а
1
= 6,1" и а
г
=
= 7,9". Найти с. к. о. третьего угла ($
3
, вычисленного по двум измеренным уг-
лам.
Ответ: о
3
— 10".
2.68. Измерены две линии: одна длиной 210,0 м с точностью т
1
= 8,9 см
и вторая — длиной 180,0 м о точностью щ = 8,1 см. С какой точность» будут
вычислены расстояния, равные: а) сумме линий и б) их разности?
114

РИС, 36
Ответ: 12 см.
2.69. Определить.*!, к. о. измерения угла теодоли-
том одним полным приемом, если с. к. о. измере
ния одного направления равен 0,5".
Ответ: 0,5*.
2.70. Измерены направления Ж/, как показано на
рис. 36, и вычислены углы = — Два угла,
имеющие общую сторону, зависимы между собой (см.
задачу 1.225). Коэффициент корреляции между такими
углами гу = —0,5 при г = / + 1. Средние квадрати-
ческие ошибки измерения направлений одинаковы и
равны т. Найти среднюю квадратическую ошибку сум-
мы всех углов.
4
Решение. Имеем функцию и = 2Р{.
Применяя формулу (2.93'), получим
«и =
4т
$ +
2т
\ (
г
и +
Г
П + '14 +'гя + г.
л
+ г
34
) =
= 4т$ + {г
и
+ г
м
+ г
34
);
Так как все гц = 0 для / ф I + 1, окончательно получаем
т
1 =
4т
1 ~
Зт
з =
т
1 = 2т». (2.98)
ЭТОТ результат, очевидно, шраведлив и для любого числа углов. Заметим, что
если пренебречь зависимость» углов, то вместо формулы (2.98) мы получили бы
т
2
= 4т
2
= 8т», (2.99)
а в общем случае т
а
= т^ \Гп.
2.71. Определить среднюю квадратическую ошибку вычисленной длины
волны модулированного светового потока
%
=> с//, если скорость света с =
= 299792,5 км/с± 0,4 км/с (т
с
), а частота, равная / = 10000,0 кГц, определена
со средней квадратической ошибкой т/ =* 0,15 кГц.
Ответ: т.
0,45 мм.
2.72. Известна средняя квадратическая ошибка измерения угла способом
повторений /Пр = 6". Определить среднюю квадратическую ошибку суммы двух
смежных углов Р] и Р,.
Решение. Составим функцию
(2.100)
Как известно, ошибки значений смежных углов, измеренных способом пов-
торений, корреляционно связаны (через ошибку общего направления), причем
г = —0,25. Применяя для оценки точности формулу (2.93'), для функции (2.100)
запишем
или
т
г
= У2— 2 • 0,25т
2
= т, V 1,5 да 7,3".
Если бы не была учтена корреляция ошибок, то было бы т/
:
2.73. Дана матрица
/ 0,50 + 0,25\
\+0,25 0,80/
8,5".
ЛИ
115

<3
РИС. 37
(-.
+
.>иг
5
+0
.Я) (;!)-<-.•»..*
2.74. Дана матрица
/0,70 +0,50 + 0,20\
М
г
= I 0,60 +0,45
V 0,80/
для отметок трех узловых точек нивелирной сети (рис. 37).
Найти матрицу М\ трех превышений.
Ответ:
/0,30 0,15 0,45\
М\ = 0,50 0,65 .
V 1.Ю/
Если имеем функцию
и= /(*!, х
г
, ... ,~х
3
), (101)
где х
1
— средние значения из л^ (I =• 1, 2, ..., «) равноточных измерений х
{
, то
для истинного значения II функции (2.101) можно построить доверительный ин-
тервал
и
— Ц
т
а < V + «а, (2.102)
где величина от
и
вычисляется по формуле (2.93) или (2.93') с аргументами от-
вместо т
х
, а т^ = т/Уп
г
. Средняя квадратическая ошибка от определяется
выражением (2.67), коэффициент выбирается из таблиц распределения Стью-
дента по доверительной вероятности Р и числу степеней свободы [7]
г = 2 11 — от, (2.103)
1=1
Этому же значению равно число степеней свободы для определения коэффи-
циентов у
1
и у
2
для доверительного интервала
7
1
от
ц
< а„ < 7
г
т
а
. (2.104)
2.75. В треугольнике один угол измерен 5 раз, а второй 9 раз с одинаковой
точностью измерения в одном приеме. Средние значения измеренных углов
Р! = 40°18'19,5" и Р
2
= 59°30'20,0". Построить доверительные интервалы для
истинного значения третьего угла и с. к. о. ст^ , приняв Р = 0,95, если т
х
=
= 0,89", от- = 0,67".
Ре ш е н и е. Угол Р
8
= 180° — ?! — Р
2
= 80°1Г20,5". Далее находим
от
?>
= У0,89
2
+ 0,67
2
= 1,11". По формуле (2.103) г = 5 + 9 — 2 = 12. Вы-
брав из таблиц прил. V коэффициент ^ = 2,2, вычисляем т
а
= 2,2
«
1,1 =>
= 2,4 и строим доверительный интервал
80°
11'
18,1" < С/ < 80°1Г22,9".
116
для двух узловых точек нивелирной сети. Найти
среднюю квадратическую ошибку превышения меж-
ду ними.
Решение. Составляем функцию
Н
= #
кон
—
— //
Н
ач и матрицу А = (—1 + 1). Далее согласно
формуле (2.94) находим = АМ*А
Т
или

Так как у
1
= 0,717, у
2
= 1,651 (прил. VIII), то 0,60" < а < 1,83".
2.76. Построить доверительный интервал для истинного значения угловой
невязки полигонометрического хода, содержащего 8 вершин, и еа дисперсии, ес-
ли каждый угол был измерен 8 приемами с ошибкой одного приема т =» 5", а
невязка оказалась равной а> = —10,2".
В случае если аргументы функции — разнородные величины или неравно-
точные с неизвестными дисперсиями, для построения интервала (2.102) число
степеней свободы [4]
5 \
а
1=\
х
1)
V—]— г
4
{=п
п
1 —
1
*1
где I = —.
йх
{
2.77. Построить доверительный интервал в условиях задачи 2.75, если
угол измеряли с ошибкой одного измерения т = 2", а угол р
2
— с ошибкой
т= 3". _
Решение. Находим ошибки т^ = 2/]^5 = 0,89", /лр- = 3 /]/"9" =
= 1,0", т
э>
= 1^0,89
2
+ 1,0
2
= 1,3". Величина
(0,89
2
+^0
2
)
2
3,21
— II»
1 1 0,282
— 0,89
4
+ — 1,0
2
Коэффициент = 2 в согласно (2.102)
80°11' 17,9" <11 <80°11"23,1".
Еслй аргументы функции и содержат не только случайные, но и система-
тические ошибки то среднюю квадратическую ошибку функции и получим
по формуле т
г
и
= т
2
„ + с
%
и
, где ошибка т
и
определяется по формулам (2.93)
или (2.93'), а величина
п п
1=1
Аналогично
Ч = + (2-106)
Заметим, что величина т
2
и
(или а
2
ц
) оценивает точность относительно ис-
тинного значения функции, а т
2
и
(или а\) — относительно математического
ожидания функции, т. е. точность самого процесса измерений.
2.78. Найти дисперсию а
2
и
в условиях задачи 2.64, если каждый угол
содержит систематическую ошибку = 0,5".
Решение. На основании формул (2.105) и (2.106) находим
" -2
Сц = 2
= т = 5
"
;
=90 + 25= 115.
/=1
2.79. Решить задачу 2.67, если с
а
= 1", = 0,5".
Ответ: о
7
= 10,1".
2.80. Решить задачу 2.70, если каждое измеренное направление содержало
систематическую ошибку с^ = 1".
117

§ 23. ОЦЕНКА ТОЧНОСТИ ПО РАЗНОСТЯМ ДВОЙНЫХ РАВНОТОЧНЫХ
ИЗМЕРЕНИЙ
Если имеем двойные равноточные измерения п величин Х
и
Х
г
,
Х
п
и получены результаты
* ^
9 9
I
то составляем разности
— х'
{
. (2.107)
При отсутствии систематических ошибок эти разности можно рас-
сматривать как ошибки величин, истинное значение которых равно
0. Поэтому, применяя формулу Гаусса, имеем
Для среднего значения х
1ср
= + х\)12 получаем
т =3*-=-^. (2.Ю9)
ср 2 у2~
х
'
На наличие в постоянной систематической ошибки укажет зна-
чительное отклонение от нуля величины
В = 1й]/п. (2.110)
В этом случае, рассматривая разности
—9 (2.111)
как уклонения от арифметической средины и применяя формулу Бес-
селя, получим
(2Л12)
Формулы для /ад, и (2.109) остаются в силе и в этом случае. Конт-
ролем вычислений служит формула Ы'] = —яр, где р = Э
окр
— 0.
На основании формулы (2.60) напишем неравенство [3]
| № | < 2,5[ | а | ]/уТ, (2.113)
при выполнении которого можно принять гипотезу об отсутствии в
разностях й
х
постоянной систематической ошибки*.
2.81. В табл. 23 даны результаты нивелирования (превышения в м) между
точками при двух положениях нивелира. Вычислить средние квадратические
ошибки одного измерения и среднего из двойных измерений.
* В учебнике [3] приведено более жесткое неравенство < 0,25[|^|],
при соблюдении которого величина та не будет искажена систематическими
ошибками в пределах точности ее вычисления.
118
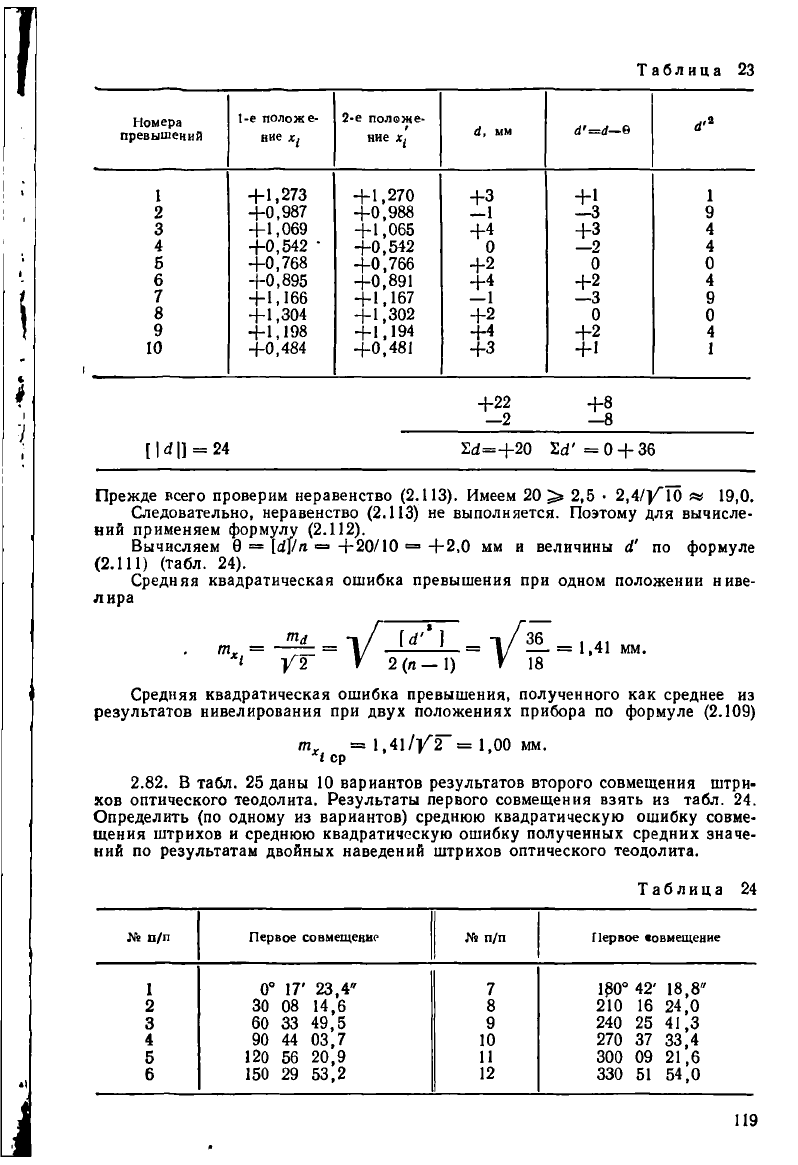
Таблица 29
Номера
1-е положе-
2-е положе-
й, мм
<*'=<*—е
а-
2
превышений
ние х^
ние
й, мм
<*'=<*—е
1
+1,273
+ 1,270
+3
+1
1
2
+0,987
+0,988
—1 —3 9
3
+1,069
+1,065
+4
+3
4
4
+0,542 '
+0,542
0 —2
4
5
+0,768
+0,766
+2
0 0
6
+0,895
+0,891
+4
+2 4
7
+ 1,166
+1,167 — 1
—3
9
8
+1,304
+1,302
+2
0
0
9
+ 1,198
+1,194
+4
+2
4
10
+0,484 +0,481
+3
+1
1
+22 +8
—2 —8
[|<*|] = 24 2<*=+20 &Г =0 + 36
Прежде всего проверим неравенство (2.113). Имеем 20 > 2,5 • 2,4/|^10 да 19,0.
Следовательно, неравенство (2.113) не выполняется. Поэтому для вычисле-
ний применяем формулу (2.112).
Вычисляем 9 = Ы\1п = +20/10 = +2,0 мм и величины Л' по формуле
(2.111) (табл. 24).
Средняя квадратическая ошибка превышения при одном положении ниве-
лира
. ,41 мм.
х
' /2 V 2 (п — 1) V 18
Средняя квадратическая ошибка превышения, полученного как среднее из
результатов нивелирования при двух положениях прибора по формуле (2.109)
т = 1,41//2~= 1,00 мм.
I ср
2.82. В табл. 25 даны 10 вариантов результатов второго совмещения штри-
хов оптического теодолита. Результаты первого совмещения взять из табл. 24.
Определить (по одному из вариантов) среднюю квадратическую ошибку совме-
щения штрихов и среднюю квадратическую ошибку полученных средних значе-
ний по результатам двойных наведений штрихов оптического теодолита.
Таблица 24
№ п/п
Первое совмещение
7
8
9
10
11
12
1$0° 42' 18,8"
210 16 24,0
240 25 41,3
270 37 33,4
300 09 21,6
330 51 54,0
119
Первое совмещение
0° 17' 23,4"
30 08 14,6
60 33 49,5
90 44 03,7
120 56 20,9
150 29 53,2
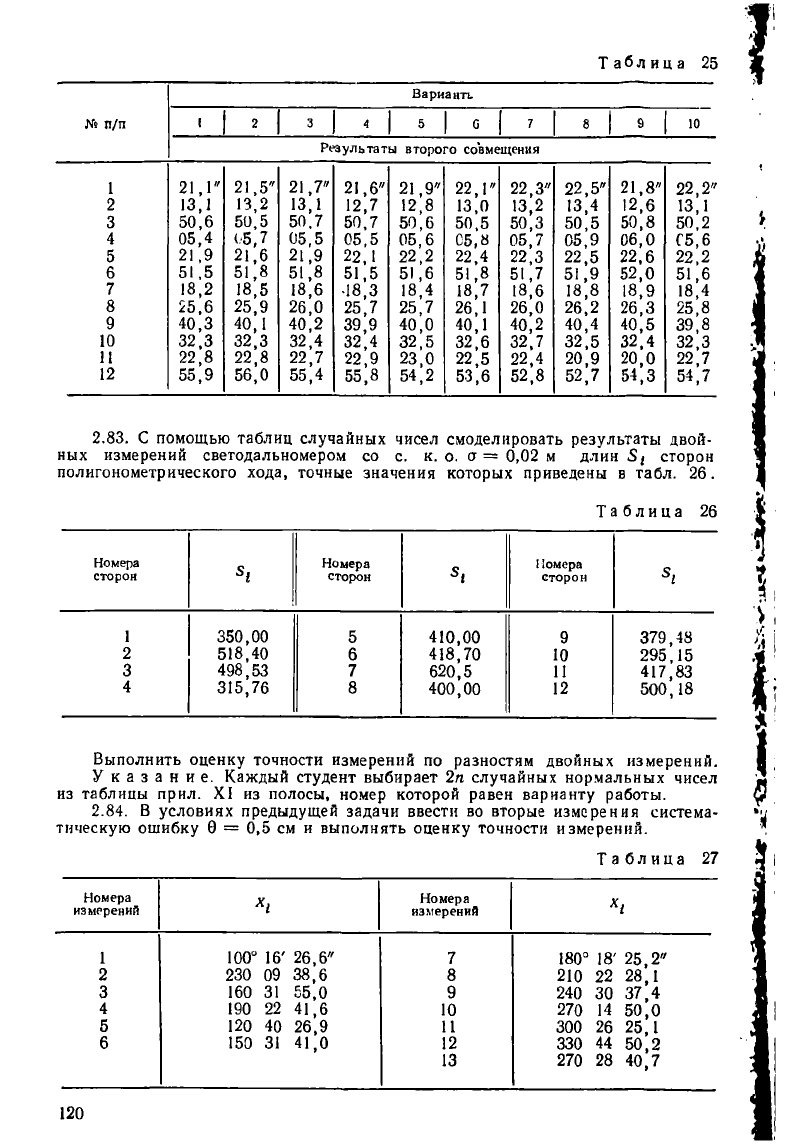
Таблица 29
Вариант!.
Результаты второго совмещения
21,1"
13.1
50,6
05.4
21,9
51.5
18.2
55.6
40,3
32,3
22,8
55,9
21,5"
13.2
50.5
(,5,7
21.6
51.8
18,5
25.9
40,1
32.3
22,8
56,0
21,7"
13.1
50.7
05.5
21,9
51.8
18.6
26,0
40.2
32,4
22,7
55,4
21,6"
12,7
50,7
05,5
22,1
51,5
•18,3
25.7
39,9
32,4
22,9
55.8
21,9"
12,8
50,6
05,6
22,2
51.6
18.4
25.7
40,0
32.5
23,0
54,2
22,1"
13.0
50.5
С5,8
22.4
51,8
18,7
26.1
40,1
32.6
22.5
53.6
22,3"
13.2
50.3
05,7
22.3
51,7
18,6
26,0
40,2
32.7
22.4
52.8
22,5"
13.4
50.5
05,9
22,5
51,9
18,8
26,2
40.4
32.5
20,9
52,7
21,8"
12,6
50.8
06,0
22,6
52,0
18.9
26.3
40,5
32.4
20,0
54,3
2.83. С помощью таблиц случайных чисел смоделировать результаты двой-
ных измерений светодальномером со с. к. о. о — 0,02 м длин 5, сторон
полигонометрического хода, точные значения которых приведены в табл. 26.
Таблица 26
Номера
Номера
1
Еомера
сторон
сторон сторон
1
350,00
5
410,00 9 379,48
2
518,40
6 418,70
10 295,15
3 498,53 7
620,5 11
417,83
4
315,76 8
400,00
12
500,18
Выполнить оценку точности измерений по разностям двойных измерений.
Указание. Каждый студент выбирает 2 п случайных нормальных чисел
из таблицы прил. XI из полосы, номер которой равен варианту работы.
2.84. В условиях предыдущей задачи ввести во вторые измерения система-
тическую ошибку 9 = 0,5 см и выполнять оценку точности измерений.
Таблица 27
Номера
измерений
7
8
9
10
11
12
13
180° 18' 25,2"
210 22 28,1
240 30 37,4
270 14 50,0
300 26 25,1
330 44 50,2
270 28 40.7
100° 16' 26,6"
230 09 38,6
160 31 55,0
190 22 41,6
120 40 26,9
150 31 41,0
120

2.85. Смоделировать результаты измерений п — 13 углов полигонометри-
ческого хода двумя приемами со стандартом а = 3" измерения в каждом при-
еме и выполнять оценку точности результатов измерений. Истинные значения
углов приведены в табл. 27 (см. указание к задаче 2.83).
§ 24. НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. ПОНЯТИЕ ВЕСА. ВЕС ФУНКЦИИ
ИЗМЕРЕННЫХ ВЕЛИЧИН
Неравноточными называются измерения, дисперсии которых не
равны между собой. В этом случае дисперсия определяется формулой
°? = о*/Д, (2.114)
где 0о = с = сопз!:, постоянная для всех измерений произвольно
выбираемая величина, а — так называемые веса измерений. Из
формулы (2.114) следует определение веса
Р, =<%<$. (2-П5)
т. е. вес — величина, обратно пропорциональная дисперсии. Веса -г-
величины относительные. О весе имеет смысл говорить, когда число
измерений л > 1. Приняв = 1, устанавливаем смысл а\. Так как
при этом <то = о?, то Оо есть дисперсия измерения, вес которого при-
нят за единицу (сокращенно — дисперсия единицы веса).
Измерение с весом р = 1 может быть как реально существующим,
так и фиктивным.
В случае когда дисперсии о? неизвестны, вес вычисляют по приб-
лиженной формуле
р
1
= \*1т}, (2.116)
где тI — средняя квадратическая ошибка «-го измерения, а величи-
на р., введенная вместо а
0
, — ошибка единицы веса. Для применения
формулы (2.116) ошибка т
1
должна быть определена надежно (полу-
чена из результатов измерений, число которых п > 8), а также сво-
бодна от систематического влияния.
Часто, пользуясь свободой выбора о
0
(или р), веса измерений мож-
но установить, не зная а
4
(или т{). Приведем примеры.
. Пример 1. Пусть одним и тем же инструментом измерено п линий дли-
ной 5/. Полагая известным коэффициент случайного влияния а
1м
, можно напи-
сать
Тогда
Р
31
= °о/
Полагая а = о
1м
, получим
Р
ч
=1/5*. (2.117)
Здесь из измерения с весом 1 принято фиктивное измерение линии длиной 5 =
= 1 м.
121

Пример 2. Измерено несколько углов одним и тем же инструментом
числом приемов Л{ каждый. Найти веса средних значений каждого угла. Обозна-
чая с. к. о. измерения угла одним приемом через а
х
, имеем
с
Р
= А/
п
ь Р1 = °о/ ср = °о V •
Полагая а
0
= с^, получаем
Р1 = п. (2.118)
За измерение с весом 1 принято измерение угла одним приемом.
ПримерЗ. Одним и тем же инструментом «измерена» сумма углов П;-
угольника (например, найдена сумма углов в треугольнике; я, = 3). Найти вес I
суммы. Обозначая через а
х
с. к. о. измерения одного угла в я,-угольнике, полу-
чаем с. к. о. суммы углов а, = а
х
Уп
1
и вес = а^/а^л,.
Полагая а = о
и
получаем
Р1 = 1/л,. (2.119)
За единичный принят вес одного измеренного угла.
Отметим, что при вычислении весов однородных результатов из-
мерений по формулам (2.115) или (2.116) размерность с = о1 (или
р.
2
) принимают равной размерности о\п%). В этом случае вес есть
величина безразмерная.
При вычислении весов неоднородных измерений (например, углов
и линий) постоянную с считают величиной безразмерной. При этом
размерность веса равна размерности измерения в степени —2, а раз-
мерность дисперсий должна совпадать в размерностью результатов
измерений.
При вычислении весов достаточно удерживать две значащие цифры.
2.86. Дана функция и = хУр. Найти вес
Ри
, если х — результат измерения,
а р — его вес (2.120).
Решение. — = —= 1.
Ра Р
Вывод: если результат измерения умножить на корень квадратный из
его веса, то полученный результат будет иметь вес, равный 1. На этом основано
приведение неравноточных измерений к равноточным.
2.87. В треугольнике измерены три угла со средними квадратическими ошиб-
ками т
1
одного измерения и числом приемов, соответственно равными т
х
=
= 3", п
х
= 4; т
2
= 4", я
2
= 9, и т
3
= б", я
3
= 12. Найти веса среднего зна-
чения каждого угла и вес невязки, приняв за ошибку единицы веса ошибку щ.
Решение. Веса средних значений углов определим по формуле
Рг
=
И
2
/Л1?, где М
{
= т^Уп^ причем (л =
Имеем
2 О
Щ
т
1 9
Щ т\ 16
т\ 9
Рз=-ГП
3
= —-. 12 = 4,3.
т| 25
Вес невязки найдем по формуле (2.121). где
з
и = 180
е
— 2р., а именно
122

1 /Ри = 11Р1 + 1 /Р2 + 1/Рз = 0,25 + 0,20 + 0,23 = 0,68.
2.88. Найти вес приращения координат Длг = 5 соза, приняв за ошибку едини- '
цы веса ц: а) ошибку т
3
, б) ошибку т
а
.
Решение. Имеем —— = соз
2
а — + 5
2
5Ш
2
а —— .
Р Ах Рз Ра
а) Веса р
5
= ц
2
/т| = 1, р
а
= т|/т
2
.
Примечания: 1) ошибку т
а
следует выразить в радианах (т
а
/р),
2) так как измерения неоднородны и |х — величина безразмерная, то вес р
3
имеет
размерность м
-2
, вес р
а
— величина безразмерная. Обратный вес 1/р
Дл:
имеет
размерность м
-2
; б) веса р
3
= п?
а
!гг?
8
(размерность м
-2
), р
а
= т
2
/т
2
— 1 (ве-
личина безразмерная).
Размерность 1 /р
Дх
равна м
2
. В обоих случаях вес р
Ах
имеет одинаковую раз-
мерность, равную м~
2
.
2.89. Площадь многоугольника определялась разбивкой его на местности
на треугольники и трапеции. Веса площадей отдельных фигур получились сле-
дующие: р
х
= 4, р
г
= 2, рз =3, /74 = 6.
Определить вес площади многоугольника.
Ответ: 4/5.
2.90. При нивелировании отсчеты по рейке делались по трем нитям. Вес
отсчета по крайней нити в 2 раза меньше веса отсчета по средней нити. Приняв
вес отсчета по крайней нити за единицу, найти веса простой и общей арифмети-
ческих средин из отсчетов по трем нитям.
О т в е т: 3,6 и 4,0.
2.91. Найти обратный вес функции и = *
2
± ...± х
п
), где к — по-
стоянная величина, если вес каждого аргумента равен р.
2.92. В треугольнике один угол измерен я
х
раз со средней квадратической
ошибкой одного измерения т
г
. Второй угол измерен л
2
раз со средней квадрати-
ческой ошибкой т
2
. Найти средние квадратические ошибки и веса средних зна-
чений всех трех углов треугольника, приняв за единицу вес среднего значения
первого угла по одному из вариантов значений т
х
, /л
а
, п
1г
и га
2
, приведенных в
табл. 28.
Ответ:
1) />! = 1,00; р
2
= 2,16; р
3
= 0,685; 2) = 1,00; р
2
= 0,808; р
3
= 0,446;
3) = 1,00; р
2
= 0,376; р
8
= 0,274; 4) р
х
= 1,00; р
2
= 0,393; р
3
= 0,282;
5) р
х
= 1,00; р
2
= 0,031; р
3
= 0,030; 6) р
х
= 1,00; р
г
= 0,243; р
3
= 0,194;
7) р
х
= 1,00; р
а
= 0,643; р
3
= 0,605; 8) р
х
= 1,00; р
2
= 10,6; р
8
= 0,914;
9) р! = 1,00; р
2
= 14,1; р
3
= 0,935; 10) р
х
= 1,00; р
2
= 0,510; р
8
•= 0,484.
Учитывая формулу (2.115) и выражение дисперсии (2.93'), легко получить
формулу для вычисления обратного веса функции и = !(*!, х
2
х
п
) зависимых
аргументов в виде
1=1 ' К1
Г
Х
1 *)
Таблица 28
Варианты
12,0
4,0
3.2
2.3
6
8
9
10
4
10,0
7.0
8,0
6.1
9,2
6
7
8
9
10
9
10
3
4
12
4,5
2,5
6,2
7,1
1.5
123
