Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Conditional

Convergence

We have seen that the alternating harmonic series

n51

ð21Þ

n11

=n is convergent

(Example 1) but not absolutely convergent (Example 5). This suggests that there is

an interesting class of series that converge but do not converge absolutely.

DEFINITION

If a series

n51

converges but does not converge absolutely,

then we say that the series converges conditionally.

⁄ EX

AMPLE 8 For what positive values of p is the alternating p-series

n51

ð21Þ

n11

conditionally convergent?

Solution For p . 1,

the series

n51

jð21Þ

n11

j is just the convergent p-series

n51

1=n

. Therefore

n51

ð21Þ

n11

is absolutely convergent for 1 , p.By

deﬁnition, an absolutely convergent series is not conditionally convergent.

Now suppose that 0 , p # 1.

The series

n51

jð21Þ

n11

j is the divergent

p-series

n51

1=n

. Thus

n51

ð21Þ

n11

is not absolutely convergent. Because

5 1/n

decreases to 0 as n tends to inﬁnity, the series

n51

ð21Þ

n11

is con-

vergent by the Alternating Series Test. We conclude that

n51

ð21Þ

n11

conditionally convergent for 0 , p # 1 and for no other positive values of p.

QUICK QUIZ

1. True or false: If 1 2 1/3 1 1/5 2 1/7 1 1/9 is used to approximate

n51

ð21Þ

n21

=ð2n 2 1 Þ, then the error is less than 0.1.

2. For what values of p is the series

n51

ð21Þ

conditionally convergent?

3. True or false: If

n51

is conditionally convergent, then

n51

j is divergent.

4. True or false: Every series is either absolutely convergent or conditionally

convergent or divergent.

Answers

1. True 2. 0 , p # 1

3. True 4. True

EXERCISES

Problems for Practice

c In each of Exercises 1212, the given series may be shown

to converge by using the Alternating Series Test. Show that

the hypotheses of the Alternating Series Test are satisﬁed. b

n51

ð21Þ

1 1

n51

ð21Þ

ﬃﬃﬃ

n51

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

n52

ð21Þ

lnðnÞ

n51

ð21Þ

n11

ð2=3Þ

n51

ð21Þ

n11

n51

ð24=5Þ

n 1 2

n51

ð21Þ

n11

1 1

n52

ð21Þ

n11

10.

n51

ð21Þ



1 1





1 1



8.4 Alternating Series 665

11.

n52

cosðπnÞsinðπ=nÞ

12.

n51

ð21Þ

ðπ=2 2 arctanðnÞÞ

c In each of Exercises 13236, determine whether the given

series

converges absolutely, converges conditionally, or

diverges. b

13.

n51

ð21Þ

1 1

14.

n51

ð21Þ

ﬃﬃﬃ

15.

n51

ð21Þ

1 1

16.

n51

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

17.

n52

ð21Þ

lnðnÞ

18.

n51

ð21Þ

2=3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 e

19.

n51

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃ

1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

20.

n51

ð21Þ

n11

ð2=3Þ

21.

n51

ð21Þ

n11



n 1 lnðnÞ



3=2

22.

n52

ð21Þ

ðnÞ

23.

n51

sinðnÞe

24.

n51

ð21Þ

ðnÞ

1=3

25.

n51

ð21Þ



lnðnÞ



26.

n51

ð21Þ

1 1 sinðnÞ

27.

n51

ð21Þ



1 1 1=n



28.

n51

ð21Þ



en 1 1

πn 1 1



29.

n51

ð21Þ

ð1 1 1=nÞ

30.

n51

ð21Þ

ð1 1 1=nÞ

31.

n51

ð21Þ

ð1 2 1=nÞ

32.

n51

ð21Þ

arctanðnÞ

2 n

33.

n51

ð21Þ

34.

n52

ð21Þ

lnðnÞ

lnðn

35.

n53

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

lnðnÞ

36.

n53

ð21Þ

nln

ðnÞ

c In each of Exercises 37242, a convergent alternating series

S 5

n51

ð21Þ

n11

is given. Use inequality (8.4.1) to ﬁnd a

value of N such that the partial sum S

n51

ð21Þ

n11

approximates the given inﬁnite series to within 0.01. That is,

ﬁnd N so that jS 2 S

j# 0.01 holds. b

37.

n51

ð21Þ

n11

ﬃﬃﬃ

38.

n51

ð21Þ

n11

39.

n51

ð21Þ

n11

2n 2 1

40.

n51

ð21Þ

n11

41.

n51

ð21Þ

n11

1 15n

42.

n51

ð21Þ

n11

lnðn 1 1Þ

Further Theory and Practice

c In each of Exercises 43246, ﬁnd a value of M for which the

Alternating Series Test may be applied to the tail

n5M

ð21Þ

of the given series

n51

ð21Þ

. b

43.

n51

ð21Þ

2 20n 1 101

44.

n51

ð21Þ

2 32n

1 400

45.

n51

ð21Þ

46.

n51

ð21Þ

lnðn

ﬃﬃﬃ

c In each of Exercises 47250, calculate the given alternating

series

to three decimal places. b

47.

n51

ð21Þ

48.

n51

ð21Þ



1 1 1=n



666 Chapter 8 Inﬁnite Series

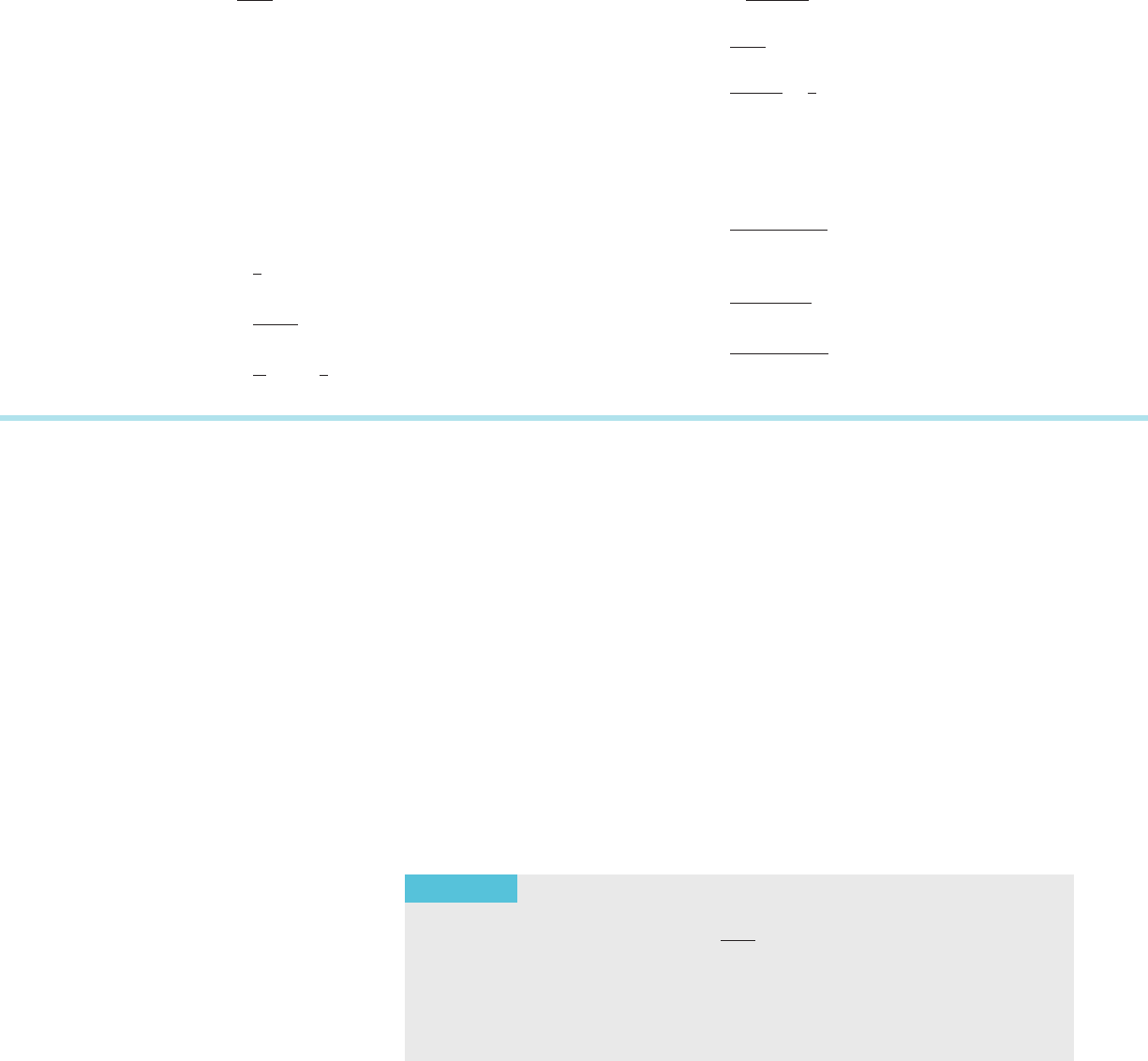
49.

n51

ð21Þ

ð2nÞ!

50.

n51

ð21Þ

22n

Calculator/Computer Exercises

c In each of Exercises 51256, an equation is given that

expresses the value of an alternating series. For the given d,

use the Alternating Series Test to determine a partial sum

that is within 5 3 10

2(d11)

of the value of the inﬁnite series.

Verify that the asserted accuracy is achieved. b

51.

n51

ð21Þ

n11

5 lnð2Þ d 5 2

52.

n51

ð21Þ

n11

2n 2 1

5 π d 5 2

53.

n51

ð21Þ

n11

5 1 2

d 5 5

54.

n51

ð21Þ

n11

ð2n 2 1Þ!

5 sinð1Þ d 5 5

55.

n50

ð21Þ

ð2nÞ!

5 cosð1Þ d 5 5

56.

n50

ð21Þ

ðπ=3Þ

ð2nÞ!

d 5 5

c In each of Exercises 57260, ﬁnd a value of M for

which the

Alternating Series Test may be applied to the tail

n5M

ð21Þ

of the given series

n51

ð21Þ

. b

57.

n51

ð21Þ

1 13

1 55n 1 60

58.

n51

ð21Þ

lnðnÞ

59.

n51

ð21Þ

100n

9=4

1 n

150 1 n

5=2

60.

n51

ð21Þ

expð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n=100

8.5 The Ratio and Root Tests

There are two powerful and easy-to-use tests that tell when a series converges

absolutely: the Ratio Test and the Root Test. We will discuss them in this section.

Bear in mind, however, that they are of no use in telling whether a series converges

conditionally.

The Ratio Test Suppose that

n51

is a series of pos itive terms for which each term a

n11

approximately equal to a ﬁxed multiple L of its predecessor a

. That is, suppose

that a

n11

L a

for every n. For n 5 1 and n 5 2, we have a

L a

and a

L a

Because a

L a

L (L a

), we conclude that a

L

a

. Similarly,

L a

L (L

a

) 5 L

a

. By continuing this process, we obtain the estimate

L

n21

a

for each positive integer n.

Now, if the approximate ratio L is less than 1, then the series

n51

will

converge by comparison with the convergent geometric series a

n51

n21

.On

the other hand, if the approximate ratio L is greater than 1, then a

n11

. a

, and the

terms of the series do not tend to 0. In this case, the series diverges by the

Divergence Test. These are the ideas behind the next test.

THEOREM 1

(The Ratio Test) Let

n51

be a series. Suppose that

lim

n-N



n11



5 L:

a. If L , 1, then the series converges absolutely.

b. If L . 1, then the series diverges.

c. If L 5 1, then the Ratio Test gives no information.

8.5 The Ratio and Root Tests 667

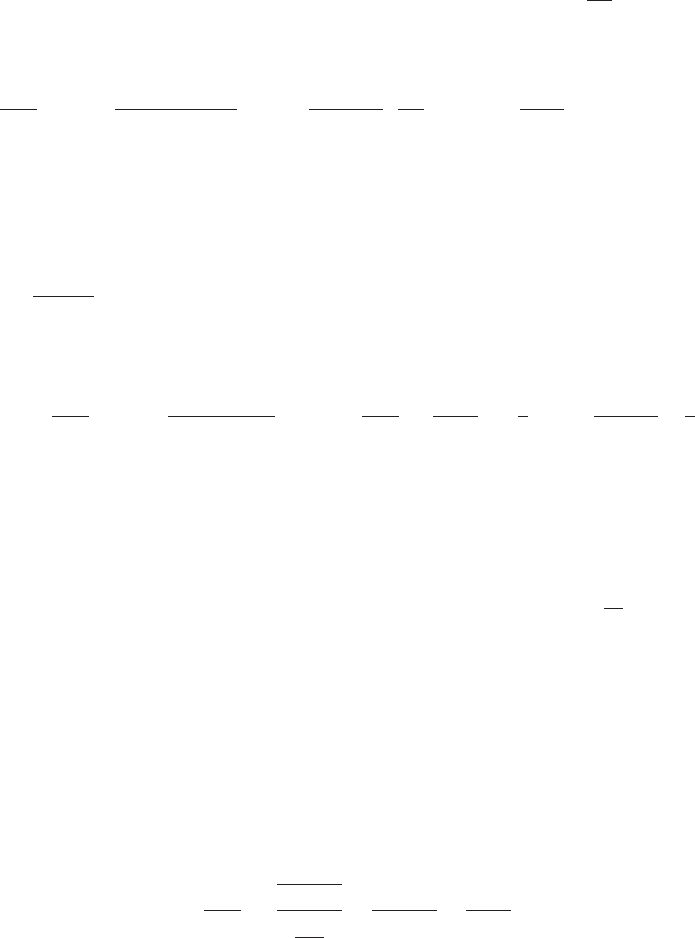
Take particular notice that the Rat io Test yields no information when L 5 1. This

point will be made clearer in the examples. Also remember that the limit of the

ratio ja

n11

j might not even exist. In this case, we cannot use Theorem 1. Finally,

notice that the test only depends on the limit of the ratio ja

n11

j. The outcome

does not depend on the ﬁrst million or so terms of the series, and that is the way it

should be: The convergence or divergence of a seri es depends only on its tail.

Now we look at some examples that illustrate when the Ratio Test gives

convergence and when it gives divergence.

⁄ EX

AMPLE 1 Use the Ratio Test to analyze the series

n51

Solution We

set a

5 2

. Then, as -N,

L 5 lim

n-N



n11



5 lim

n-N

n11

=ðn 1 1Þ

5 lim

n-N

n11

ðn 1 1Þ



5 lim

n-N



n 1 1



5 2  1

5 2:

Because L . 1, the Ratio Test says that the series diverges. (The Divergence Test

also can be used to reach this conclusion.)

⁄ EXAMPLE 2 Discuss the convergence or divergence of the series

n51

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

Solution In

this example, we let a

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

. Then,

L 5 li

n-N



n11



5 lim

n-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 2

n11

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

5 lim

n-N



n11



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 2

n 1 1



lim

n-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 2=n

1 1 1=n

Part a of the Ratio Test then tells us that the series converges. (As a matter of style

the adjec tive “absolute” is generally not used in discussions about the convergence

of a series of positive terms a

. Doing so would add no information because

n51

.) ¥

⁄ EXAMPLE 3 Use the Ratio Test to show that the series

n50

converges

for every real num ber x.

Solution Recall

that 0! 5 1, 1! 5 1, and n! 5 n (n 2 1) (n 2 2) 3 2 1. When

using the Ratio Test, it is easiest to spot cancellation when a larg er factorial is

written in terms of a smaller one. Thus

ðn 1 1Þ! 5 ðn 1 1Þn ðn 2 1Þðn 2 2Þ

3  2  1

5 ðn 1 1Þn!:

Let a

5 x

/n!, so that



n11



jxj

n11

ðn 1 1Þ!

jxj

jxjn!

ðn 1 1Þ!

jxj

n 1 1

668 Chapter 8 Inﬁnite Series

As n -N, the limit of this expression is 0. Therefore L 5 lim

n-N

n11

exists and is less than 1. By part a of the Ratio Test, we conclude that the series

converges.

INSIGHT

The Ratio Test often works well when the general term a

of a series

factors into powers and factorials. In such cases, the ratio ja

n11

j can simplify greatly

due to cancellation, as Example 3 illustrates.

⁄ EXAMPLE 4 Test the series

n51

for convergence.

Solution Set a

5 n

/n!. Then



n11



ðn 1 1Þ

n11

=ðn 1 1Þ!

=n!



n 1 1





1 1



This last expression converges to the number e when n-N, as we know from

Section 2.6 in Chapter 2. Because e 5 2.718 . . . . 1, the series diverges. Exercise 64

contains some further remarks about this example.

⁄ EXAMPLE 5 Apply the Ratio Test to the harmonic series

n51

1=n.

Solution Setting a

5 1/n, we have

lim

n-N



n11



5 lim

n-N

1=ðn 1 1Þ

1=n

5 lim

n-N

n 1 1

5 1:

Therefore the Ratio Test gives no information whatever. Of course we already

know from independent reasoning that the harmonic series diverges.

⁄ EXAMPLE 6 Apply the Ratio Test to the series

n51

1=n

Solution Set a

5 1/n

. Then,

lim

n-N



n11



5 lim

n-N

1=ðn 1 1Þ

1=n

5 lim

n-N

ðn 1 1Þ

5 lim

n-N



n 1 1



5 1

5 1:

Therefore the Ratio Test gives no information. Of course we already know from

independent reasoning that this series is a con vergent p-series.

INSIGHT

Examples 5 and 6 together explain what we mean when we say that the

Ratio Test gives no information when the limit L is equal to 1. Under these circum-

stances, the series could diverge (Example 5), or the series could converge (Example 6).

There is no way to tell when L 5 1; you must use another convergence test to ﬁnd out.

8.5 The Ratio and Root Tests 669

The Root Test The next test, the Root Test, has a simila r ﬂavor to the Ratio Test. Sometimes it is

easier to apply the Ratio Test than it is to apply the Root Test (and vice versa).

Thus even though the tests look rather similar, you should be well-versed in using

both of them.

THEOREM 2

Let

n51

be a series. Suppos e that lim

n-N

1=n

5 L.

a. If L , 1, then the series converges absolutely.

b. If L . 1, then the series diverges.

c. If L 5 1, then the test gives no information.

The Root Test is based on a comparison with a tail of the geometric series

n51

. If lim

n-N

1=n

5 L, then there is an N such that ja

jL

for all n $ N.

Thus we compare

n5N

j with the geometric series

n5N

, which is con-

vergent when L , 1 and divergent when L . 1. Once again, take particular note

that when L 5 1, the Root Test gives no information. Also, the limit L might not

even exist. In this case, we cannot use Theorem 2. Finally, the Root Test does not

depend on the ﬁrst million or so terms of the series—only on the tail.

When applying the Root Test, the limit formula

lim

n-N

1=n

5 1 ð8:5:1Þ

is often useful. We have considered this limit already (Example 4 of Section 8.1),

but let us give a quick reminder of its proof. We use the basic form ula

lim

x-N

lnðxÞ

5 0, which is limit formula (8.3.1) with q 5 1. It then follows that

lim

n-N

1=n

5 lim

n-N

exp



lnðn

1=n



5 lim

n-N

exp



lnðnÞ



5 exp



lim

n-N

lnðnÞ



5 e

5 1:

Examples Now we look at some examples that will illustrate when the Root Test gives

convergence, when it gives divergence, and when it gives no informat ion.

⁄ EX

AMPLE 7 Analyze the series

n51

ðn

1 6Þ

Solution We apply the Root Test with a

5 n/(n

1 6)

. Then, ja

1/n

5 n

1/n

/(n

1 6).

The numerator of this express ion tends to 1 by equation (8.5.1). Because the

denominator becomes unbounded, we have L 5 lim

n-N

1=n

5 0. Because this

limit is less than 1, the Root Test tells us that the series converges.

INSIGHT

Notice that

ðn

1 6Þ

2n21

Thus the series from Example 7 is termwise dominated by the convergent p-series

n51

1=n

. We can therefore deduce that the given series converges by applying the

Comparison Test for Convergence. The Root Test, however, proves to be more

straightforward to apply in this example.

670 Chapter 8 Inﬁnite Series

⁄ EXAMPLE 8 Apply the Root Test to the series

n53

ðnÞ

Solution When a

5 1/ln

(n), we have ja

1/n

5 1/ln(n). This expression tends to 0

as n-N. Therefore L 5 0 , 1, and the Root Test says that the series converges.

INSIGHT

Try using the Ratio Test or the Integral Test on the series of Example 8.

Each of those tests results in a difﬁcult calculation. The Root Test is an obvious

choice for Example 8 because a

is a n

power. The Comparison Test for Convergence

might also be used. For example, ln(n) is greater than 2 for n $ 8. Therefore 1/ln

(n) ,

1/2

for n $ 8. We deduce that the given series is convergent by comparison with the

convergent geometric series

n58

1=2

⁄ EXAMPLE 9 Apply the Root Test to the series

n51

ð22Þ

Solution With a

5 (22)

, we have

lim

n-N

1=n

5 lim

n-N

10=n

ðlim

n-N

1=n

ð8:5:1Þ

. 1:

We conclude, using the Root Test, that the series diverges.

⁄ EXAMPLE 10 Let p be positive. Apply the Root Test to the p-series

n51

1=n

Solution If a

5 1/n

, then

L 5 lim

n-N

1=n

j5 lim

n-N

1=n

p=n

ðlim

n-N

1=n

ð8:5:1Þ

Whatever the value of p, the Root Test is inconclusive.

INSIGHT

Example 10 explains what we mean when we say that the Root Test gives

no information when the limit L is equal to 1. Under these circumstances, the series could

diverge (a p-series with p # 1) or the series could converge (a p-series with p . 1). There

is no way to tell from the Root Test; you must use another test to ﬁnd out.

QUICK QUIZ

1. True or false: The Ratio Test fails if applied to a series

n51

for which

lim

n-N

n11

j5 N.

2. True or false: The Ratio Test always fails when applied to a conditionally

convergent series.

3. What is lim

n-N

1=n

4. Determine whether

n51

=ð210Þ

converges absolutely, converges con-

ditionally, or diver ges.

Answers

1. False 2. True 3. 1 4. converges absolutely

8.5 The Ratio and Root Tests 671

EXERCISES

Problems for Practice

c In each of Exercises 1212, use the Ratio Test to determine

the convergence or divergence of the given series. b

n51

100

n51

ðn 1 12Þ

n51

ﬃﬃﬃﬃ

 7

n51

1 n

10.

n51

3n 1 n

11.

n51

ﬃﬃﬃ

12.

n51

1 n

c In each of Exercises 13224, verify that the Ratio Test

yields

no information about the convergence of the given

series. Use other methods to determine whether the series

converges absolutely, converges conditionally, or diverges. b

13.

n52

ð21Þ

lnðnÞ

14.

n52

ð21Þ

lnðn

15.

n51

ð21Þ

lnðnÞ

16.

n51

ð21Þ



n 1 1

1 1

17.

n51

ð21Þ





1 1



18.

n51

ð21Þ

ﬃﬃﬃ

n 1 4

19.

n51

ð21Þ

1 lnðnÞ

 n

20.

n51

ð21Þ

1 n

21.

n51

ð23Þ

1 3

22.

n51

ð21Þ



n! 1 2

23.

n51

ð21Þ

arctanðnÞ

24.

n51

ð21Þ

sin





c In each of Exercises 25234, use the Root Test to deter-

mine

the convergence or divergence of the given series. b

25.

n51

2n=2

26.

n51

27.

n51

28.

n51

29.

n51

100

ð1 1 nÞ

30.

n52

ðnÞ

31.

n53



lnðnÞ

lnðn

2 4Þ



32.

n51





33.

n51



1 7n 1 13

1 1



34.

n51



1 2



Further Theory and Practice

c In Exercises 35240, use the Ratio Test to determine the

convergence or divergence of the given series. b

672 Chapter 8 Inﬁnite Series

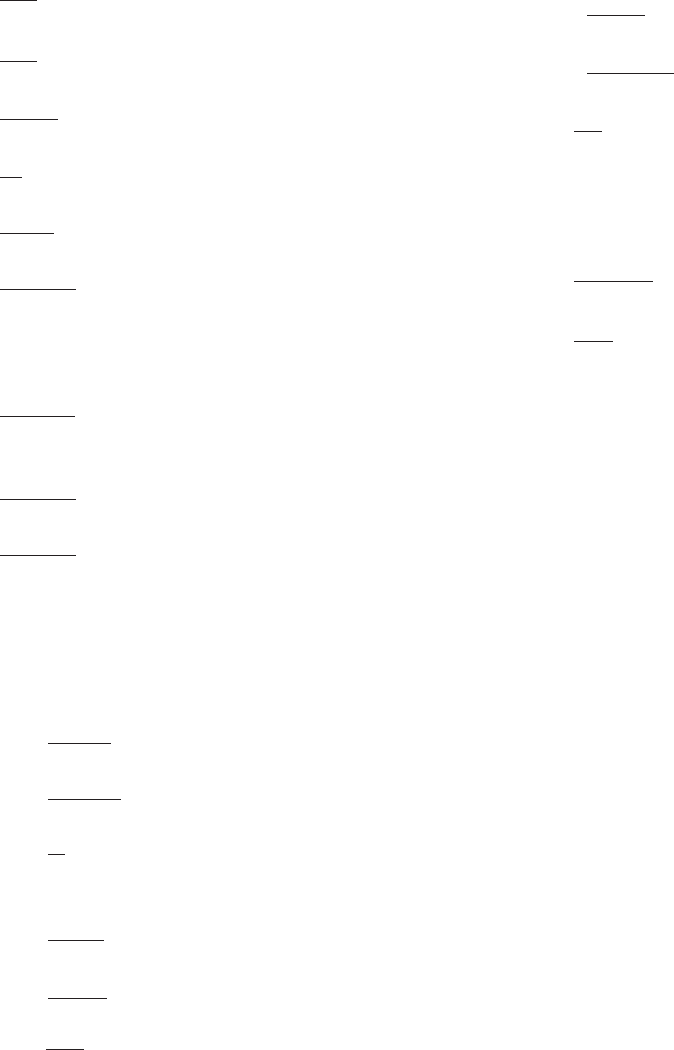
35.

n51

ð2nÞ!

ð3nÞ!

36.

n51

ðn!Þ

ð2nÞ!

37.

n51

ð2nÞ!

ðn!  2

38.

n51

39.

n51

n 1 3

1 2

40.

n51

1 1 ln

ðnÞ

c In each of Exercises 41244, use the Root Test to deter-

mine

the convergence or divergence of the given series. b

41.

n51

ðn

1=n

12Þ

42.

n51

ðn

1=n

11=2Þ

43.

n51

1 1 ln

ðnÞ

44.

n51

expðnÞ

1 1 ln

ðnÞ

c In each of Exercises 45260, determine whether the series

converges

absolutely, converges conditionally, or diverges.

The tests that have been developed in Section 5 are not the

most appropriate for some of these series. You may use any

test that has been discussed in this chapter. b

45.

n51

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 10

46.

n51

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 10

47.

n51

ð21Þ

48.

n51

ð23=4Þ

49.

n51

ð21Þ

2 11

50.

n52

ð21Þ

n ln

ðnÞ

51.

n52

ð21Þ

1=n

lnðnÞ

52.

n51

ð21Þ

lnðn

1=n

53.

n51

ð21Þ



1=n

1 1 1=n



54.

n51

ð21Þ



1 2n 1 2

1 7



55.

n51

ð21Þ

1=n

56.

n51

ð21Þ

lnð2 1 1=nÞ

57.

n51

ð21Þ

lnð1 1 1=nÞ

58.

n51

ð21Þ

n 2

59.

n51

ð21Þ

ð1 1 1=nÞ

60.

n51

ð21Þ

lnðnÞ

ﬃﬃﬃ

61. Let p be a ﬁxed real number (possibly negative). Show

that the Ratio Test results in the same conclusion when

applied to both

n51

and

n51

. Explain how this

observation can save work in the application of the Ratio

Test. Deduce that the Ratio Test is inconclusive when

applied to all p-series.

62. Suppose that p is a polynomial. Show that the Ratio Test

results in the same conclusion when applied to both

n51

pðnÞa

and

n51

63. Let p be a ﬁxed real number (possibly negative). Show

that the Ratio Test results in the same conclusion when

applied to both

n52

ðnÞ and

n52

64. In Example 4, the Ratio Test is used to show that

n51

=n! diverges. Use the Divergence Test to reach

the same conclusion. However, the Divergence Test says

nothing about

n51

n!=n

. Use the calculation of Exam-

ple 4 to show that this series converges.

Calculator/Computer Exercises

c Let {a

} be a sequence of positive numbers. In a course on

mathematical analysis, one learns that if the two limits

lim

n-N

n11

and lim

n-N

1=n

exist, then they are equal. In

each of Exercises 65268, produce a plot that illustrates the

equality

of these two limits. Your plot should include a hor-

izontal line that is the asymptote of the points {(n, a

n11

)}

and {(n, a

1/n

)}. b

65. a

5 1/n

66. a

5 n/2

67. a

5 e

/ln(1 1 n)

68. a

5 n!/n

8.5 The Ratio and Root Tests 673

8.6 Introduction to Power Series

The simplest functions that we know are those that are of the form x / x

where n

is a nonnegative integer: The constant function f (x) 5 x

5 1, the functions g(x) 5 x,

h(x) 5 x

, and so on. These functions are easy to understand and simple to com-

pute. We use them to form polynomials a

1 a

x 1 1 a

, which are also

straightforward to handle. Now that we understand the concept of “inﬁnite series,”

it is natural to create functions by summing inﬁnitely many powers of x.

DEFINITION

An expression of the form a

1 a

x 1 a

1 a

1 , where the

’s are constants, is called a power series in x. It is convenient to denote the

constant term a

by a

so that we may use sigma notation to express the power

series a

1 a

x 1 a

1 a

1 as

n50

⁄ EX

AMPLE 1 Are the inﬁnite series

n50

ﬃﬃﬃ

n53

ð2xÞ

and

n50

ðx

power series in x?

Solution In

the deﬁnition of a power series, each power of x that appears is a

nonnegative integer. Therefore the series

n50

ﬃﬃﬃ

n50

n=2

5 1 1

ﬃﬃﬃ

x 1 x

ﬃﬃﬃ

1  is not a power series. The series

n53

ð2xÞ

n53

may be

written as 0 1 0 x 1 0 x

1 2

x

1 2

x

1 

Therefore

n53

ð2xÞ

is a power

series even though it begins with the index n 5 3. Similarly,

n50

ðx

5 1 1 x

1 x

1 5 1 1 0  x 1 x

1 0  x

1 1  x

1 

is a power series.

Notice that the power series a

1 a

x 1 a

1 converges for x 5 0 because it

reduces to its initial term a

when x 5 0. Thus the set on which the series

n50

converges is not empty; it contains the point 0 at the least. We may therefore regard

n50

as a function of x . The domain of this function is the (nonempty) set of x

for which the series converges.

⁄ EX

AMPLE 2 For what values of x does the power series f ðxÞ5

n50

converge?

Solution Compare

n50

with the left side of equation (8.1.2). The only

difference is that here we are using x instead of r. Thus we see that f (x)isa

geometric series with ratio x. As we know from Section 1, it converges when jxj, 1

and diverges when jxj$ 1. Thus the function f is deﬁned for x 2(21, 1). From our

study of geometric series, we know that f (x) 5 1/(1 2 x) for these values of x.

Radius and Interval

of Convergence

The set of values at which a power series converges always has a special form.

Suppose, for example, that the power series

n50

converges at some x 5 t and

that jsj, jtj. Then, lim

n-N

j5 0 by the Divergence Test (Section 8.2). In par-

ticular, we have ja

j# 1 for sufﬁciently large n. For such n, and for r 5 jsj/jtj,we

see that r , 1andja

j5 r

ja

t

j# r

. We conclude that

n50

j converges

674 Chapter 8 Inﬁnite Series