Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


P
N
n51
a
n
, we compute the partial sum S
N
5 a
1
1 a
2
1 a
3
1 1 a
N
for large integer
values N and take the limit of S
N
as N tends to infinity. We define
P
N
n51
a
n
to be the limit
S 5 lim
N-N
S
N
5 lim
N-N
ða
1
1 a
2
1 a
3
1 1 a
N
Þ, if it exists. Although we call S the
“sum” of the series, it is not a sum in the conventional sense of the word: By definition, it
is a limit.
Examples ⁄ EXAMPLE 7 Does the series
X
N
n51
1
2
n21
converge? If so, to what limit?
Solution In
Example 6, we calculated the N
th
partial sum S
N
5 2 2 1/2
N 2 1
of this
infinite series. We may now pass to the limit:
lim
N-N
S
N
5 lim
N-N
2 2
1
2
N21
5 2:
By definition, we say that the series
X
N
n51
1
2
n21
converges to 2. ¥
⁄ EXAMPLE 8 Discuss convergence for the series
P
N
n51
ð21Þ
n
521 1 1 2
1 1 1 2 1 1
.
Solution If N is
even then the partial sum S
N
5
P
N
n51
ð21Þ
n
521 1
1 2
:::
2 1 1 1 comprises an equal number of 11’s and 21’s. Therefore S
N
5 0
for N even. If N is odd, then there is one more 21 than 1 1 in the sum
S
N
5
P
N
n51
ð21Þ
n
and S
N
521. Therefor e the sequence fS
N
g
N
N51
of partial sums is
just the sequence 21, 0, 21, 0, 21, 0, . . . which does not converge. We conclude
that the series
P
N
n51
ð21Þ
n
does not converge. ¥
INSIGHT
Example 8 sheds some light on the apparent contradiction that we
encountered in Example 1. When we first investigated the series
P
N
n51
ð21Þ
n
5
21 1 1 2 1 1 1 2 1 1
,
we formed two different groupings of its summands. Those
groupings suggested different values, 21 and 0, for the series. Now we understand that
21 is the limit of the odd partial sums, and 0 is the limit of the even partial sums. The
partial sums taken together do not have a limit, and the series therefore does not con-
verge. The lesson is that we should not attempt to perform arithmetic operations on
series that do not converge.
b A LOOK BACK It is important to understand the difference between a sequence,
which is a list of numbers, and a series, which is a sum (or a limit of a sum) of
numbers. A sequence a
1
, a
2
, a
3
, . . . is used to create an infinite series
a
1
1 a
2
1 a
3
1
.
In turn, this series gives rise to a second sequence, the sequence
a
1
, a
1
1 a
2
, a
1
1 a
2
1 a
3
, . . . of partial sums of the infinite series. We determine
whether we can assign a value to the infinite series
P
N
n51
a
n
by examining the
limiting behavior of its sequence of partial sums.
A Telescoping Series It is relatively rare to find an explicit formula for the partial sums of an infinite
series. In the ne xt example, we employ a useful algebraic “trick” to evaluate the
partial sums.
8.1 Series 635
⁄ EXAMPLE 9 Discuss convergence for the series
X
N
n51
1
nðn 1 1Þ
.
Solution If
you use a calculator to compute some partial sums, then you will
probably be convinced that the series converges. We can justify this conclusion by
writing each summand in its partial fraction decomposition:
1
nðn 1 1Þ
5
1
n
2
1
n 1 1
:
As a result, we have
S
N
5
1
1 2
1
1
2 3
1
1
3 4
1 1
1
N ðN 1 1Þ
5
1
1
2
1
2
1
1
2
2
1
3
1
1
3
2
1
4
1 1
1
N 2 1
2
1
N
1
1
N
2
1
N 1 1
:
Almost everything cancels, and we have S
N
5 1 2 1/(N 1 1). Clearly lim
N-N
S
N
5 1.
Therefore the series
X
N
n51
1
nðn 1 1Þ
converges to 1.
¥
INSIGHT
If we set f (n) 5 1/n, then we may write the series of Example 9 in the form
X
N
n51
f ðnÞ2 f ðn 1 1Þ
:
In general, a series that may be expressed this way is said to be a collapsing or telescoping
series. That is because each partial sum collapses to two summands:
X
N
n51
f ðnÞ2 f ðn 1 1Þ
5
f ð1Þ2 f ð2Þ
1
f ð2Þ2 f ð3Þ
1
f ð3Þ2 f ð4Þ
1
1
f ðN 2 1Þ2 f ðNÞ
1
f ðNÞ2 f ðN 1 1Þ
5 f ð1Þ2 f ðN 1 1Þ:
Such a series converges if and only if lim
N-N
f ðNÞ5 0.
The Harmonic Series The infinite series
P
N
n51
1=n comesupofteninmathematicsandphysics.Itiscalled
the “harmonic series” because of its role in the theory of acoustics: If the natural
frequencies at which a given body vibrates are ρ
1
, ρ
2
,... andif ρ
n
/ρ
n11
5 1/(n 1 1) for
all n, then the frequencies are said to form a sequence of harmonics. Although the
harmonic series is divergent, you might not think so if you calculate a large number of
partial sums using a computer. The divergence is taking place so slowly that it is
difficult to be certain what is actually happening. For example, if we sum the first
1 million terms, then we obtain S
1 000 000
5 14.3927 (rounded to four decimal places).
If we add the next 1,000 terms to this, then we obtain S
1 001 000
514.3937—the change is
barely noticeable despite the additional 1,000 terms! If you sum the first 10
43
terms of
the harmonic series, then the result is a value that is still less than 100. To be certain of
the divergence, we need a mathematical proof.
THEOREM 1
The harmonic series
X
N
n51
1
n
is divergent.
636 Chapter 8 Infinite Series
Proof. Notice that
S
1
5 1 5
2
2
S
2
5 1 1
1
2
5
3
2
S
4
5 1 1
1
2
1
1
3
1
1
4
$ 1 1
1
2
1
1
4
1
1
4
$ 1 1
1
2
1
1
2
5
4
2
S
8
5 1 1
1
2
1
1
3
1
1
4
1
1
5
1
1
6
1
1
7
1
1
8
$ 1 1
1
2
1
1
4
1
1
4
1
1
8
1
1
8
1
1
8
1
1
8
5
5
2
:
In general, this argument shows that S
2
k
$ ðk 1 2Þ=2: The sequence of S
N
’s is
increasing because the series contains only positive terms. The fact that the partial
sums S
1
, S
2
, S
4
, S
8
, . . . increase without bound shows that the entire sequence of
partial sums must increase without bound. We conclu de that the series diverges. ’
Basic Properties of
Series
We now present some elementary properties of series that are similar to the
properties of sequences that you learned in Chapter 2.
THEOREM 2
Suppose that
P
N
n51
a
n
converges to A, that
P
N
n51
b
n
converges to
B, that
P
N
n51
c
n
diverges, and that λ is a constant. Then
a.
P
N
n51
ða
n
1 b
n
Þ converges to A 1 B, and
P
N
n51
ða
n
2 b
n
Þ converges to A 2 B.
b.
P
N
n51
ðλa
n
Þ converges to λA.
c.
P
N
n51
ðλc
n
Þ diverges if λ 6¼0.
⁄ EX
AMPLE 10 Discuss convergence of the series
X
N
n51
5
nðn 1 1Þ
2
3
2
n21
.
Solution Examp
le 9 combined with Theorem 2b tells us that
P
N
n51
5
1
nðn 1 1Þ
converges to 5. Similarly, Example 7 and Theorem 2b tell us that
P
N
n51
3
1
2
n21
converges to 3 2, or 6. Hence, by Theorem 2a, we may conclude that the given
series converges to 5 2 6, or 21.
¥
⁄ EXAMPLE 11 Let a
n
5
2
n
2 n
n2
n
. Does the series
P
N
n51
a
n
converge?
Solution We
may write the summand a
n
as
a
n
5
2
n
2 n
n2
n
5
2
n
n2
n
2
n
n2
n
5
1
n
2
1
2
n
:
8.1 Series 637

Let b
n
5 1/2
n
. Because b
n
5 λ
1
2
n21
with λ 5 1/2, we know from Example 7 and
Theorem 2b that
P
N
n51
b
n
converges. If the series
P
N
n51
a
n
were to converge, then so
would the series
P
N
n51
ða
n
1 b
n
Þby Theore m 2a. But a
n
1 b
n
5 1/n, and we know that
the harmonic series diverges (Theorem 1). Therefore
P
N
n51
a
n
must diverge. ¥
INSIGHT
The method used to solve Example 10 shows that if
P
N
n51
a
n
converges
and
P
N
n51
b
n
diverges, then
P
N
n51
ða
n
1 b
n
Þ diverges.
Series of Powers
(Geometric Series)
We now consider the series
P
N
n50
r
n
5 1 1 r 1 r
2
1 r
3
1 of all nonnegative
integer powers of a fixed number r. We call this series a geometric series with ratio r.
Notice that this series begins with index value n 5 0. Occasionally, it will be useful
to begin such series, and others, with a first summation index value that is an
integer M not equal to 1.
THEOREM 3
If jrj, 1, then the geometric series with ratio r converges and
X
N
n50
r
n
5
1
1 2 r
: ð8:1:13Þ
In general, for any M in Z,ifjrj, 1, then
P
N
n5M
r
n
converges and
X
N
n5M
r
n
5
r
M
1 2 r
: ð8:1:14Þ
If 1 # jrj, then the series
P
N
n50
r
n
and
P
N
n5M
r
n
diverge.
Proof. Let S
N
5
P
N21
n50
r
n
5 1 1 r 1 r
2
1 1 r
N21
denote the N
th
partial sum of
the geometric series
P
N
n50
r
n
.If1# r, then it is clear that S
N
satisfies
S
N
5 1 1 r 1 r
2
1 1 r
N21
$ 1 1 1 1 1 1 1 1 5 N. It follows that the
sequence {S
N
} cannot converge to any real number ‘. In other words, the series
P
N
n50
r
n
is divergent for 1#r. We put aside the case r #21 for now. (In Section 8.2,
we will see how to prove this divergence without analyzing partial sums.)
Now suppose that jrj, 1.
Then, using formula (8.1.12), we have
S
N
5
X
N21
n50
r
n
5 1 1 r 1 r
2
1 1 r
N21
5
r
N
2 1
r 2 1
:
Because jrj, 1, we have lim
N-N
r
N
5 0 and
X
N
n50
r
n
5 lim
N-N
S
N
5
0 2 1
r 2 1
5
1
1 2 r
;
which is equation (8.1.13). Finally, if jrj, 1 and if M is any integer, then we deduce
equation (8.1.14) from (8.1.13) as follows:
X
N
n5M
r
n
5 lim
N-N
X
M1N
n5M
r
n
5 lim
N-N
ðr
M
1 r
M11
1 r
M12
1 1 r
M1N
Þ
5 r
M
lim
N-N
ð1 1 r 1 r
2
1 1 r
N
Þ5 r
M
1
1 2 r
5
r
M
1 2 r
:
’
638 Chapter 8 Infinite Series

⁄ EXAMPLE 12 At a certain aluminum recycling plant, the recycling pro-
cess turns x pounds of used aluminum into 0.9x pounds of new aluminum. Including
the initial quantity, how much usable aluminum will 100 pounds of virgin aluminum
ultimately yield, if we assume that it is continually returned to the same recycling
plant?
Solution We
begin with 100 pounds of aluminum. When it is returned to the plant
as scrap and recycled, 0.9 100 pounds of new aluminum results. When that
aluminum is returned to the plant as scrap and recycled, 0.9 (0.9 100) 5 0.9
2
100
pounds of new aluminum results. This process continues forever. Writing the initial
quantity of aluminum as 0.9
0
100, and using formula (8.1.13) and Theorem 2b, we
see that the total amount of aluminum created is
0:9
0
100 1 0:9 100 1 0:9
2
100 1 5
X
N
n50
ð0:9
n
100Þ5 100
X
N
n50
0:9
n
5 100
1
1 2 0:9
5 1000:
Therefore 1000 pounds of usable aluminum is ultimately generated by an initial 100
pounds of virgin aluminum.
¥
⁄ EXAMPLE 13 Express the repeating decimal 1212.121212121 . . . as a ratio
of two integers.
Solution There
are several ways we can apply formula (8.1.14) with r 5 1/100. For
example, choosing M 5 1, we have
1212:12121212
1::: 5 1212 1 0:12 1 0:0012 1 0:000012 1
5 1212 1 12
1
100
1
1 12
1
100
2
1 12
1
100
3
1
5 1212 1 12
X
N
n51
1
100
n
5 1212 1 12
ð1=100Þ
1 2 ð1=100Þ
5 1212 1 12
1
99
5
40000
33
:
Alternatively, we can use formula (8.1.14) with r 5 1/100 and M 521 as follows:
1212:121212121::: 5 1200 1 12 1 0:12 1 0:0012 1 0 :000012 1
5 12
1
100
21
1 12
1
100
0
1 12
1
100
1
1 12
1
100
2
1 12
1
100
3
1
5 12
X
N
n521
1
100
n
5 12
ð1=100Þ
21
1 2 ð1=100Þ
5 12
10000
99
5
40000
33
: ¥
8.1 Series 639

QUICK QUIZ
1. Which of the numbers 9/8, 10/8, 11/8, 12/8, is a partial sum of
P
N
n51
n=2
n
?
2. True or false: The sum of two convergent series is also convergent.
3. What is the value of
P
N
n50
5=3
n
?
4. Does
P
N
n51
5=n converge or diverge?
Answers
1. 11/8 2. True 3. 15/2 4. Diverge
EXERCISES
Problems for Practice
c In each of Exercises 1220, evaluate lim
n-N
a
n
for the
given sequence {a
n
}. b
1. a
n
5
2n
2
2 1 1 n
3
5n
3
1 n 1 2
2. a
n
5
3n
2
1 n 1 4
2n
3
1 1
3. a
n
5
2
n11
1 5
2
n
1 3
4. a
n
5
3
2n
1 2
9
n11
1 1
5. a
n
5
3
n
1 2 5
n
2
n
1 3 5
n
6. a
n
5
2
n
1 5
n
7
n
7. a
n
5
6n 1 cosðnÞ
3n 1 2 2 sinðn
2
Þ
8. a
n
5
n2
n
1 2
n
1 1
n2
n
1 1
9. a
n
5
n2
n
1 3
n
1 1
n2
n
1 3
n
1 2
10. a
n
5
lnðnÞ
n
11. a
n
5
ln
2
ðnÞ
ffiffiffi
n
p
12. a
n
5 ne
22n
13. a
n
5 n
2
/e
n
14. a
n
5
X
n
k51
1
kðk 1 1Þ
15. a
n
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
2
1 3n
p
2 n
16. a
n
5 arcsin
n
n 1 1
17. a
n
5 arctan(n)
18. a
n
5 n sin(1/n)
19. a
n
5
n 1 1
n
n
20. a
n
5
n 2 1
n
n
c In each of Exercises 21228, a series
P
N
n51
a
n
is given.
Calculate the first five partial sums of the series. That is,
calculate S
N
5
P
N
n51
a
n
for N 5 1, 2, 3, 4, 5. b
21.
P
N
n51
1=n
22.
P
N
n51
2
n
=n!
23.
P
N
n51
ð2
2n
1 1Þ
24.
X
N
n51
1
n
2
1
n 1 1
25.
P
N
n51
2
n
=3
n
26.
P
N
n51
1=n
2
27.
P
N
n51
ð21Þ
n11
=n
2
28.
P
N
n51
n
2
=2
n
c In each of Exercises 29244, find the sum of the given
series. b
29.
P
N
n51
ð3=7Þ
n
30.
P
N
n51
ð2=3Þ
2n
31.
P
N
n50
ð22=3Þ
n
32.
P
N
n51
8
2n
33.
P
N
n50
9ð0:1Þ
n
34.
P
N
n54
ð0:2Þ
n
35.
P
N
n523
ð1=5Þ
n
36.
P
N
n51
7
ð2n=3Þ
37.
X
N
n52
1
2
n=2
38.
P
N
n521
ð2=3Þ
2n11
39.
P
N
n53
ð0:1Þ
n
=ð0:2Þ
n12
40.
P
N
n53
ð2
2n
1 3
2n
Þ
41.
P
N
n51
ð2
2n
3
2n
1 7
2n
Þ
42.
P
N
n51
ð5
2n
3
2n
4
n
Þ
43.
X
N
n51
2
n11
5
n21
44.
X
N
n51
3
n21
4
n11
640 Chapter 8 Infinite Series
c In Exercises 45250, write each of the given repeating
decimals as a constant times a geometric series (the geometric
series will contain powers of 0.1). Use the formula for the sum
of a geometric series to express the repeating decimal as a
rational number. b
45. 0.8888888
. . .
46. 0.131313131313 . . .
47. 0.017017017 . . .
48. 0.983983983 . . .
49. 0.1221212121 . . .
50. 0.31323232 . . .
c In Each of Exercises 51256, the partial sum S
N
5
P
N
n51
a
n
of an infinite series
P
N
n51
a
n
is given. Determine the value of
the infinite series. b
51. S
N
5 2 2 1/N
2
52. S
N
5 (N 1 1)/(N 1 4)
53. S
N
5 (3N 1 2)/(N 1 1)
54. S
N
5 2N
2
/(N
2
1 2)
55. S
N
5 (3N 1 1)/(2N 1 4)
56. S
N
5 2 2 2
N11
/3
N12
Further Theory and Practice
c In each of Exercises 57262, prove that the given series
diverges by showing that the N
th
partial sum satisfies
S
N
$ k N for some positive constant k. b
57.
X
N
n51
ð1:01Þ
n
58.
X
N
n51
n
n 1 1
59.
X
N
n51
n
2n 1 3
60.
X
N
n51
n
ffiffiffiffiffiffiffiffiffiffiffiffiffi
n
2
1 1
p
61.
X
N
n51
4
n
4
n
1 2
n
62.
X
N
n51
n 1 10
10n
c In each of Exercises 63268, calculate the N
th
partial sum
S
N
of the given series in closed form. Sum the series by finding
lim
N-N
S
N
. b
63.
X
N
n51
1
n
2
1
n 1 1
64.
X
N
n51
n 1 1
n 1 2
2
n
n 1 1
65.
X
N
n51
2n 2 2
n
3
2
2n
ðn 1 1Þ
3
66.
X
N
n51
1
n
2
2
1
ðn 1 1Þ
2
67.
X
N
n51
1
ffiffiffi
n
p
2
1
ffiffiffiffiffiffiffiffiffiffiffi
n 1 1
p
68.
X
N
n51
arctanðn 1 1Þ2 arctan ð nÞ
c In each of Exercises 69272, use partial fractions to cal-
culate
the N
th
partial sum S
N
of the given series in closed
form. Sum the series by finding lim
N-N
S
N
. b
69.
X
N
n51
1
nðn 1 2Þ
70.
X
N
n51
1
nðn 1 4Þ
71.
X
N
n51
1
ð2n 1 1Þð2n 1 3Þ
72.
X
N
n51
2n 1 1
ðn
2
1nÞ
2
73. Calculate the N
th
partial sum of
X
N
n51
ln
n
n11
. Show
that the series is divergent.
74. Show that
X
N
n52
ln
1 2
1
n
2
5 ln
ðN 2 1Þ!
1 ln
ðN 1 1Þ!
2 2lnðN!Þ2 lnð2Þ;
and use this formula to sum
X
N
n52
ln
1 2
1
n
2
:
75. Suppose that r is a constant greater than 1. Calculate
the N
th
partial sum of
P
N
n51
r
n
ðr
n
2 1Þðr
n11
2 1Þ
; and use
the formula to evaluate the infinite series.
76. The Fibonacci sequence { f
n
} is recursively defined by
f
0
5 f
1
5 1 and f
n
5 f
n21
1 f
n22
for n $ 2. Show that
1
f
n
f
n12
5
1
f
n
f
n11
2
1
f
n11
f
n12
;
and use this formula to sum
P
N
n50
1=ðf
n
f
n12
Þ.
77. It is known that
P
N
n51
1=n
2
5 π
2
=6. What are the values of
the convergent series
1=2
2
1 1=4
2
1 1=6
2
1 1=8
2
1
and
1 1 1=3
2
1 1=5
2
1 1=7
2
1 ?
78. It is known that
X
N
n51
n
2
n
5 2 and
X
N
n51
1
n2
n
5 lnð2Þ.
Supposing that a, b, and c are constants, evaluate
X
N
n51
an
2
1 cn 1 b
n2
n
:
8.1 Series 641
79. It is known that
P
N
n51
1
n
2
5
1
6
π
2
and
P
N
n51
1
n
4
5
1
90
π
4
. Let
f ðx; yÞ5
P
N
n51
x 1 y ðπnÞ
2
n
4
. Describe the solution set
fðx; yÞ2R
2
: f ðx; yÞ5 0g.
80. The infinite series
P
N
n51
nr
n21
arises in genetics and other
fields. Notice that the partial S
N
5
P
N
n51
nr
n21
is equal to
d
dr
X
N
n51
r
n
. Use this observation to derive a closed form
expression for S
N
. Show that
P
N
n51
nr
n21
converges for
jrj, 1, and determine its value.
81. Prove that
P
N
n51
lnð1=nÞ diverges.
82. Use the inequality x/2 , ln(1 1 x) for x A (0, 1) to prove
that
P
N
n51
lnð1 1 1=nÞ diverges.
83. A tournament ping-pong ball bounces to 2/3 of its original
height when it is dropped from a height of 25 cm or less
onto a hard surface. How far will the ball travel if drop-
ped from a height of 20 cm and allowed to bounce
forever?
84. Suppose that every dollar that we spend gives rise (through
wages, profits, etc.) to 90 cents for someone else to spend.
That 90 cents will generate a further 81 cents for spending,
and so on. How much spending will result from the pur-
chase of a $16,000 automobile, the car included? (This
phenomenon is known as the multiplier effect.)
85. Suppose that the national savings rate is 5%. Of every
dollar earned, 5b is saved and 95b is spent. Of the 95b
that goes into the hands of others, 5% will be saved and
95% spent, and so on. How much spending will be gen-
erated by a 100 billion dollar ($10
11
) tax cut?
86. A heart patient must take a 0.5 mg daily dose of a med-
ication. Each day, his body eliminates 90% of the medi-
cation present. The amount S
N
of the medicine that is
present after N days is a partial sum of which infinite
series? Approximately what amount of the medicine is
maintained in the patient’s body after a long period of
treatment?
87. A particular pollutant breaks down in water as follows: If
the mass of the pollutant at the beginning of the time
interval [t, t 1 T]isM, then the mass is reduced to Me
2kT
by the end of the interval. Suppose that at intervals 0, T,
2T,3T, . . . a factory discharges an amount M
0
of the
pollutant into a holding tank containing water. After a
long period, the mixture from this tank is fed into a river.
If the quantity of pollutant released into the river is
required to be no greater than Q , then, in terms of k, T,
and Q, how large can M
0
be if the factory is compliant?
88. Sketch the graphs of y 5 x
n
, n 5 1, 2, 3, . . . in one viewing
window [0, 1] 3 [0, 1]. Find the area between two con-
secutive graphs y 5 x
n21
and y 5 x
n
. Use your calculation
to calculate
P
N
n51
1=
n ðn 1 1Þ
by a geometric argument.
89. If r is a fixed number in (0, 1), then
P
N
n51
r
n
converges.
However, if {r
n
} is a sequence of numbers in (0, 1), then
P
N
n51
r
n
n
may diverge. Prove the divergence of this series
for r
n
5 1 2 1/n.
90. Show that
2 3 6 8 ð2NÞ5 N!2
N
:
91. Show that
1 3 5 7 ð2N 2 3Þð2N 2 1Þ5
ð2NÞ!
N!2
N
:
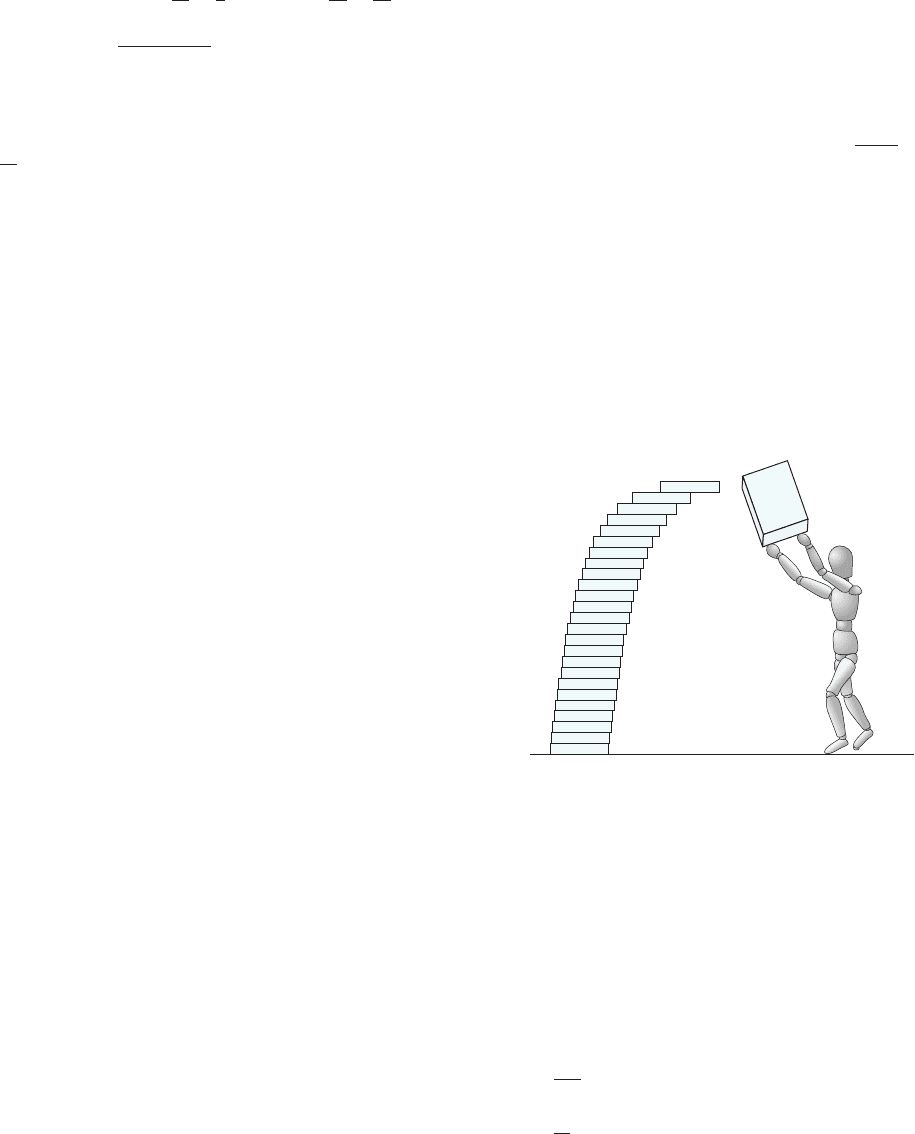
92. Mr. Woodman has an unlimited supply of 1 inch long,
3/16 inch thick dominoes. He stacks N of them so that for
each 2 # n # N, the n
th
domino, counting from the bottom
of the stack, protrudes 1/( 2(N 2 n 1 1)) inch over the end
of the (n 2 1)
st
domino (see Figure 1). Show that the
center of mass of Mr. Woodman’s tower of dominoes lies
over the bottom domino (and so the stack will not fall).
Deduce that by using a sufficiently large number N,
Mr. Woodman can make his stack span, from left to right,
any given distance. About how many dominoes would it
take to span the 10 foot length of his playroom? How high
would the tower be?
Calculator/Computer Exercises
c In each of Exercises 93297, a convergent series is given.
Estimate the value ‘ of the series by calculating its partial sums
S
N
for N 5 1, 2, 3, . . . . Round your evaluations to four decimal
places and stop when three consecutive rounded partial sums
agree. (This procedure does not ensure that the last partial sum
calculated agrees with ‘ to four decimal places. The error that
results when a partial sum is used to approximate an infinite
series is called a truncation error. Methods of estimating
truncation errors will be discussed in later sections.) b
93.
X
N
n51
e
2n
n
94.
X
N
n51
e
n
n!
m Figure 1
642 Chapter
8 Infinite Series
95.
X
N
n51
1:1
n
n
96.
X
N
n51
2
n
1 n
2
10
n
97.
X
N
n51
2n 1 1
n
5
1 n 1 1
98. Let a and b be positive numbers, and set r 5 1/(1 1 a
2b
).
Observe that 0 , r , 1, and therefore
P
N
n51
r
n
is con-
vergent. Let S denote the value of this infinite series.
a. Let τðNÞ5
P
N
n5N11
r
n
. Show that
τðNÞ5
a
bðN11Þ
ða
b
11Þ
N
:
b. For what constants α and β is ln(τ(N)) 5 α ln( a) 2β ln
(a
b
1 1)?
c. Calculate ln(τ(N)) for a 5 10, b 5 50, and N 5 10
6
.By
about how much does the millionth partial sum S
10
6
of
X
N
n51
1
1 1 10
250
n
differ from the full sum? (The difference is very large.
The number N of terms that must be summed for
S 2 S
N
to be less than 0.1 is around 1.17 3 10
52
.)
8.2 The Divergence Test and the Integral Test
In the preceding section, you learned that the convergence of a series
P
N
n51
a
n
depends on the behavior of the N
th
partial sum S
N
5
P
N
n51
a
n
5 a
1
1 a
2
1 1
a
N21
1 a
N
as N tends to infinity. The problem is that it is often difficult or impos-
sible to find an explicit formula for S
N
. Fortunately, in many cases, we do not need
such an explicit formula. Beginning in this section, we will develop “tests” that
permit us to decide whether an infinite series converges or diverges without having
to directly analyze the sequence of partial sums.
The Divergence Test To show that a series
P
N
n51
a
n
converges, we must show that the sequence {S
N
}of
partial sums converges (either directly or by using one of the theorems that will be
presented in this and subsequent sections). We may wonder whether the con-
vergence of {a
n
} itself tells us anything about the convergence of
P
N
n51
a
n
. There are
three possibilities:
a. lim
n-N
a
n
does not exist.
b. lim
n-N
a
n
exists and this limit is nonzero.
c. lim
n-N
a
n
5 0:
The next theorem tells us that, in cases a and b, the series
P
N
n51
a
n
diverges.
THEOREM 1
(The Divergence Test) If the summands a
n
of an infinite series
P
N
n51
a
n
do not tend to 0, then the series
P
N
n51
a
n
diverges.
Proof. The
statement, “A implies B,” is logically equivalent to the statement, “not
B implies not A.” This equivalence is known as the law of the contrapositive. Using
this law with A 5 ‘‘lim
n-N
a
n
6¼ 0’’ and B 5 “
P
N
n51
a
n
diverges,” we will prove the
Divergence Test in the form,
P
N
n51
a
n
converges implies lim
n-N
a
n
5 0.
We may always write a partial sum S
N
5 a
1
1 a
2
1 1 a
N21
1 a
N
in terms of
the preceding partial sum S
N21
:
S
N
5 ða
1
1 a
2
1 1 a
N21
Þ1 a
N
5 S
N21
1 a
N
:
8.2 The Divergence Test and the Integral Test 643

This equation may also be written as a
N
5 S
N
2 S
N21
. Notice that if we have
lim
N-N
S
N
5 ‘, then we also have lim
N-N
S
N21
5 ‘. As a result, if the infinite series
P
N
n51
a
n
converges to ‘, then
lim
N-N
a
N
5 lim
N-N
ðS
N
2 S
N21
Þ5 ‘ 2 ‘ 5 0: ’
Notice that the Divergence Test tells us that certain infinite series diver
ge, but
it never tells us that a particular infinite series converges. The next two examples
show how the Divergence Test can be used and how it should not be used.
⁄ EX
AMPLE 1 What does the Divergence Test tell us about the geometric
series
P
N
n50
r
n
?
Solution Let a
n
5 r
n
.Ifjrj, 1, then lim
n-N
a
n
5 0. In this case, the hypothesis of
the Divergence Test is not satisfied. The Divergence Test therefore yields no
information about the series
P
N
n50
r
n
when jrj, 1. Of course, we do know from
Section 8.1 that the series
P
N
n50
r
n
converges for jrj, 1.
Now suppose that 1 # jrj.
Then, 1 # jr
n
j, and lim
n-N
a
n
6¼ 0. In this case, the
hypothesis of the Divergence Test is satisfied. Thus the Divergence Test tells us
that
P
N
n50
r
n
diverges when 1#jrj. (This application of the Divergence Test com-
pletes the proof of Theorem 3, Section 8.1.)
¥
⁄ EXAMPLE 2 What does the Divergence Test tell us about the two series
P
N
n51
1=n and
P
N
n51
1=ðn
2
1 nÞ?
Solution The
answer is, “Not a thing!” The Divergence Test can only be applied to
infinite series
P
N
n51
a
n
for which lim
n-N
a
n
6¼ 0. That is not the case with either of
these series. We do know from Section 8.1 that
P
N
n51
1=n diverges and
P
N
n51
1=ðn
2
1 nÞ converges (Theorem 1 and Example 9, respectively). But the
Divergence Test does not provide us with an alternative justification for either of
these conclusions.
¥
INSIGHT
It is a common error to conclude that an infinite series converges because
its terms tend to 0. Such reasoning is faulty and the conclusion may be false: the harmonic
series shows that a series
P
N
n51
a
n
may be divergent even though lim
n-N
a
n
5 0. In the
theory of infinite series, it often happens that one particular test is inconclusive, which
only means that we must resort to a different line of reasoning.
Series with
Nonnegative Terms
Some series have both positive and negative terms and converge b ecause the terms
tend to cancel each other out. The situation is more straightforward when a series has
summands that are all nonnegative. Suppose that a
n
$ 0foreachn.LetS
N
5
P
N
n51
a
n
.
Notice that S
N
5 S
N21
1 a
N
, and therefore S
N 2 1
# S
N
. Thus th e sequence of partial
sums is increasing: 0 # S
1
# S
2
# S
3
# . . . . There are now only two possibilities. Either
the S
N
’s increase without bound, or they do not. If they increase without bound,
then the series diverges. On the other hand, if the S
N
’s are bounded above, then by the
Monotone Convergence Property (Section 2.6 of Chapter 2), the S
N
’s converge to a
limit ‘. In this case,
P
N
n51
a
n
5 ‘. We state this observation as a theorem.
THEOREM 2
Suppose that 0 # a
n
for each n. Let S
N
5
P
N
n51
a
n
. If there is a real
number U such that S
N
# U for all N, then the infinite series
P
N
n51
a
n
converges.
644 Chapter 8 Infinite Series
