Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.

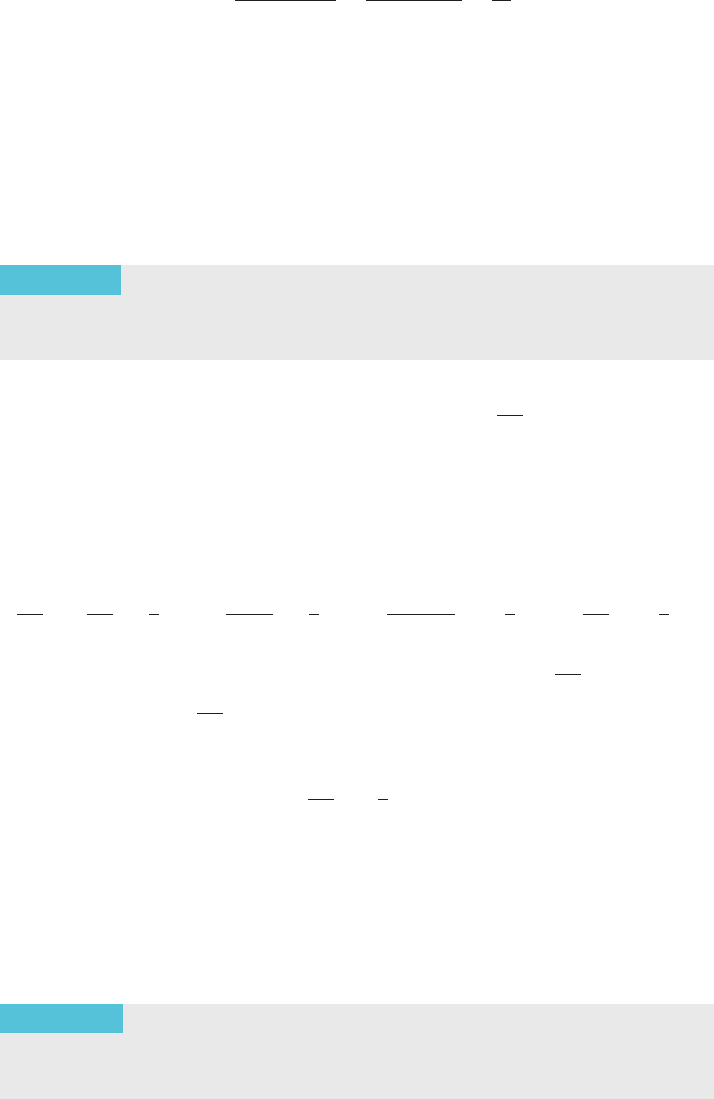
Solution Observe that
0 #
sin
2
ð2n 1 5Þ
n
4
1 8n 1 6
#
1
n
4
1 8n 1 6
#
1
n
4
:
Also,
P
N
n51
1=n
4
is a p-series that is convergent (because p 5 4 . 1). By the Com-
parison Test for Conver gence, the given series converges.
¥
An Extension of the
Comparison Test For
Convergence
Because the convergence or divergence of a seri es does not depend on the first
several terms, we can restate the Comparison Test for Convergence so that it
applies even when there are a finite number of exceptions to the termwise com-
parison 0 # a
n
# b
n
. We say that a property P holds “for all sufficiently large n”if
there is an integer M such that P holds for all n $ M.
THEOREM 2
(The Comparison Test for Convergence) Let 0 # a
n
# b
n
for all
sufficiently large n. If the series
P
N
n51
b
n
converges, then the series
P
N
n51
a
n
also
converges.
⁄ EX
AMPLE 4 Determine whether the series
X
N
n510
n
10
4
n
converges.
Solution This
series begins with large terms—the first is 10
10
/4
10
, or 9536.7.
However, the exponential in the denominator eventually catches up to the
polynomial in the numerator, exceeds it, and then continues to grow substantially
faster than the numerator. We therefore expect the series to converge. To justify
our intuition, we can reason as follows:
n
10
4
n
5
n
10
2
n
1
2
n
5
n
10
e
nlnð2Þ
1
2
n
5
n
e
nlnð2Þ=10
10
1
2
n
5
n
e
λn
10
1
2
n
;
where λ 5 ln(2)/10. Example 3 of Section 8.1 shows that lim
n-N
n
e
λn
5 0. Therefore
there is an N such that
n
e
λn
, 1 for all n $ N. Thus if a
n
5 n
10
/4
n
and b
n
5 (1/2)
n
, then
we have
a
n
5
n
10
4
n
#
1
2
n
5 b
n
for all n $ N. We compare
P
N
n5N
a
n
to the series
P
N
n5N
b
n
, which, being a geometric
series with positive ratio 1/2 (less than 1), is convergent. We conclude that the given
series that begins with summation index 10 converges as well.
¥
The Comparison Test
for Divergence
We can now reverse our reasoning to obtain a comparison test for divergence.
THEOREM 3
(The Comparison Test for Divergence) Let 0 # b
n
# a
n
for all
sufficiently large n. If the series
P
N
n51
b
n
diverges, then the series
P
N
n51
a
n
also
diverges.
8.3 The Comparison Tests 655

Proof. Suppose that there is an M such that b
n
# a
n
for all M # n.If
P
N
n51
a
n
converged, then the Comparison Test for Convergence would imply that
P
N
n51
b
n
converged, which would contradict the hypothesis. Thus
P
N
n51
a
n
must diverge. ’
⁄ EXAMPLE 5 Show that the series
X
N
n51
lnðn 1 4Þ
n
diverges.
Solution Observe
that 1 , ln(1 1 4) # ln(n 1 4) for every n $ 1. It follows that
1/n , ln(n 1 4)/n for n $ 1. Because the harmonic series
P
N
n51
1=n diverges, the
Comparison Test for Divergence allows us to conclude that the given series
diverges as well.
¥
⁄ EXAMPLE 6 Analyze the series
X
N
n52
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
nlnðnÞ
p
:
Solution Notice
that
ffiffiffi
y
p
, y if 1,y. We may apply this observation to y 5 n ln(n),
which is greater than 1 for every n $ 2. Thus each term of the given series satisfies
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n lnðnÞ
p
, n lnðnÞ and 1=ðnlnðnÞÞ, 1=
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n lnðnÞ
p
. In Example 10 of Section 8.2, we
proved that the series
P
N
n52
1=ðnlnðnÞÞ diverges. By the Comparison Theorem for
Divergence, the given series also must diverge.
¥
⁄ EXAMPLE 7 Use the Comparison Theorem for Divergence to study the
series
X
N
n51
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffiffi
n
p
1 3
p
Solution A
rough analysis tells us that we are dealing with terms that are
comparable to 1/n
1/4
for large n. Because the p-series with p 5 1/4 is divergent, we
predict that the given series diverges. We can make this informal observation
precise by noting that, for n $ 9, we have n
1/2
$ 3, or 2n
1/2
5 n
1/2
1 n
1/2
$ n
1/2
1 3, or
(2n
1/2
)
1/2
$ (n
1/2
1 3)
1/2
,or
1
ffiffiffi
2
p
1
n
1=4
#
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffiffi
n
p
1 3
p
:
The series ð1=
ffiffiffi
2
p
Þ
P
N
n51
1=n
1=4
diverges (because it is a multiple of a p-series with
p 5 1/4 , 1). Therefore the given series diverges by the Comparison Test for
Divergence.
¥
An Advanced Example The next example is more sophisticated than the preceding examples. As you read
the solution, pay particular attention to the way the logarithm is handled. The basic
principle to keep in mind is that logarithmic growth is very slow. In fact,
lim
x-N
lnðxÞ
x
q
5 0 ð8:3:1Þ
for any positive number q. To derive limit formula (8.3.1), we apply l’Ho
ˆ
pital’s
Rule as follows:
lim
x-N
d
dx
lnðxÞ
d
dx
x
q
5
1
q
lim
x-N
1=x
x
q21
5
1
q
lim
x-N
1
x
q
5 0:
Limit formula (8.3.1) tells us that ln(x)/x
q
becomes, and remains, less than 1. In
other words, for any positive q, there is an integer M such that
lnðxÞ# x
q
ðM # xÞ: ð8:3:2Þ
656 Chapter 8 Infinite Series
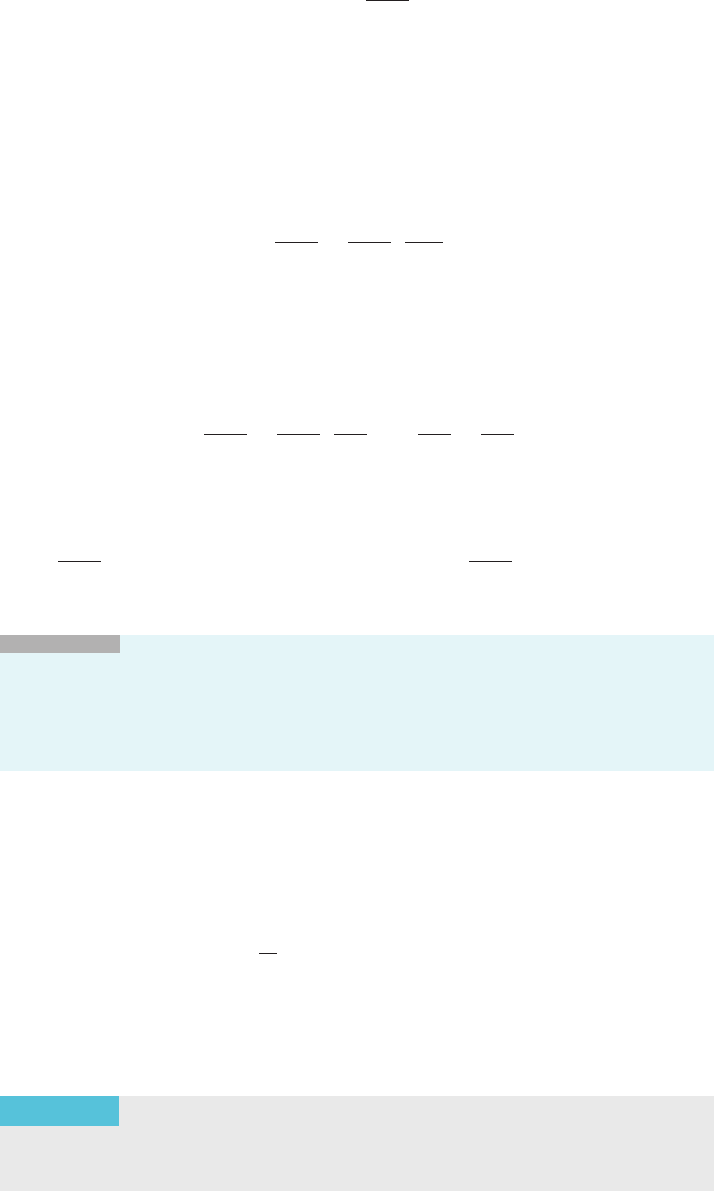
⁄ EXAMPLE 8 Does the series
X
N
n53
lnðnÞ
n
2
converge?
Solution This
series of nonnegative summands termwise exceeds the series
P
N
n53
1=n
2
. But this last series converges. Thus the Comparison Test for
Divergence does not tell us anything about the converge nce or divergence of the
series
P
N
n53
lnðnÞ=n
2
based on the comparison we have made. We must try another
approach. This time, we will analyze the size of ln(n)/n
2
more carefully . The idea is
that we can use some of the growth in the denominator to counteract the
logarithmic growth in the numerator. We write
lnðnÞ
n
2
5
lnðnÞ
n
q
1
n
22q
for a positive q that will be chosen appropriately. If 1 , 2 2 q,orq , 1, then we
may make a comparison with the convergent p-series
P
N
n53
ð1=n
22q
Þ. Choosing
q 5 1/2—any positive value less than 1 would do just as well—we see from
inequality (8.3.2) that there is an integer M such that
lnðnÞ
n
2
5
lnðnÞ
n
1=2
1
n
3=2
# 1
1
n
3=2
5
1
n
3=2
for n $ M. Because the infinite series
P
N
n5M
1=n
3=2
is a convergent p-series ( p 5
3/2 . 1), it follows from the Comparison Test for Convergence that the series
P
N
n5M
lnðnÞ
n
2
converges. Because the given series
P
N
n53
lnðnÞ
n
2
has a convergent tail, it
must also be convergent.
¥
INSIGHT
Example 8 reminds us that the comparison tests are not “if and only if”
statements. If we find a divergent series
P
N
n51
b
n
such that a
n
# b
n
, then the Comparison
Test for Convergence tells us nothing about
P
N
n51
a
n
because not all the hypotheses of
the test are satisfied. Likewise, if we find a convergent series
P
N
n51
b
n
such that a
n
$ b
n
,
then the Comparison Test for Divergence tells us nothing about
P
N
n51
a
n
.
The Limit Comparison
Test
We close this section with a variant of the comparison tests called the Limit
Comparison Test. In practice, you may find this new test easier to apply than the
Comparison Tests from Theorems 1 and 2. The idea behind this new test is also
easy to understand. If
P
N
n51
a
n
and
P
N
n51
b
n
are series of positive terms and if
‘ 5 lim
n-N
a
n
b
n
exists and 0 , ‘ , N;
then for large n, we have the approximation a
n
‘ b
n
. Because the terms of the
tail series of
P
N
n51
a
n
and
P
N
n51
b
n
are approximately proportional, we expect
the two series to have the same convergence properties. We state this as a theorem.
THEOREM 4
(The Limit Comparison Test) Let
P
N
n51
a
n
and
P
N
n51
b
n
be series
of positive terms. Suppose that ‘ 5 lim
n-N
a
n
=b
n
exists and 0 , ‘ ,N. Then
P
N
n51
a
n
converges if and only if
P
N
n51
b
n
converges.
8.3 The Comparison Tests 657

⁄ EXAMPLE 9 Does the series
X
N
n51
n
2n
3
2 4n 1 6
converge?
Solution As
discussed in the Insight following Example 1, we neglect the lower
order terms 4n and 6 in the denominator. The n
th
summand a
n
is approximately
n/(2n
3
), or 1/(2n
2
) for large values of n. This suggests that we apply the Limit
Comparison Test with the series
P
N
n51
b
n
5
P
N
n51
1=ð2n
2
Þ. We calculate
lim
n-N
a
n
b
n
5 lim
n-N
n=ð2n
3
2 4n 1 6 Þ
1=ð2n
2
Þ
5 lim
n-N
2n
3
2n
3
2 4n 1 6
5 lim
n-N
2
2 2 4n=n
2
1 6=n
3
5 1:
Because the limit is positive and finite and because the simpler series
P
N
n51
1=ð2n
2
Þ
converges, we conclude that the original series converges as well.
¥
INSIGHT
The Limit Comparison Test allows us to compare series without having to
do a term-by-term comparison. In Example 10, we are able to compare the series
P
N
n51
n=ð2n
3
2 4n 1 6Þ with the series
P
N
n51
1=ð2n
2
Þ. In doing so, we do not have to worry
about proving the inequality n/(2n
3
2 4n 1 6) # 1/(2n
2
) as we would with the Comparison
Test for Convergence. (In fact, for n . 1, this inequality is false.)
⁄ EXAMPLE 10 Show that the series
X
N
n51
2
n
1 1
n2
n
1 1
diverges.
Solution The n
th
summand a
n
5 (2
n
1 1)/(n2
n
1 1) may be written as
a
n
5 (1 1 2
2n
)/(n 1 2
2n
). It follows that a
n
1/n for large n. We apply the Limit
Comparison Test using the infinite series
P
N
n51
b
n
5
P
N
n51
1=n for comparison:
lim
n-N
a
n
b
n
5 lim
n-N
ð2
n
1 1Þ=ðn2
n
1 1Þ
1=n
5 lim
n-N
n2
n
1 n
n2
n
1 1
5 lim
n-N
1 1 1=2
n
1 1 1=ð n2
n
Þ
5 1:
Because this limit is finite and positive and because the harmonic series
P
N
n51
1=n
diverges, we conclude that the given series diverges.
¥
QUICK QUIZ
1. True or false: The Compariso n Tests yield no information about the series
P
N
n51
a
n
when 0 # b
n
# a
n
for all n and
P
N
n51
b
n
is convergent.
2. True or false: If a series
P
N
n51
a
n
of positive terms converges, then
X
N
n51
n 1 1
n
a
n
also converges.
3. True or false: It follows from the Limit Comparison Test that if
P
N
n51
a
n
is a
divergent series of positive terms and if {λ
n
} is a sequence of positive numbers
with a finite limit, then
P
N
n51
λ
n
a
n
is also divergent.
4. For what values of p is
X
N
n51
n 1 1
n
p
convergent?
Answers
1. True 2. True 3. False 4. 2 , p
658 Chapter 8 Infinite Series

EXERCISES
Problems for Practice
c In each of Exercises 1216, use the Comparison Test for
Convergence to show that the given series converges. State
the series that you use for comparison and the reason for its
convergence. b
1.
X
N
n51
n
n
3
1 1
2.
X
N
n51
5n 2 4
n
9=4
3.
X
N
n51
1
ðn 1
ffiffiffi
2
p
Þ
2
4.
X
N
n51
1
ð
ffiffiffi
n
p
1
ffiffiffi
2
p
Þ
4
5.
X
N
n51
2 1 sinðnÞ
n
4
6.
X
N
n51
2n 2 1
ne
n
7.
X
N
n51
n 1 2
2n
5=2
1 3
8.
X
N
n51
n
2
1 2n 1 10
2n
4
9.
X
N
n51
2
n
n3
n
10.
P
N
n51
ð1=3Þ
n
2
11.
X
N
n51
1
2n
ffiffiffi
n
p
2 1
12.
X
N
n51
ffiffiffi
n
p
n
2
1 1
13.
X
N
n51
n
3
n
4:01
1 1
14.
X
N
n51
2
2
n
1 1=2
n
15.
X
N
n51
1
n!
16.
X
N
n51
1
n
n
c In each of Exercises 17228, use the Comparison Test for
Divergence to show that the given series diverges. State the
series that you use for comparison and the reason for its
divergence. b
17.
X
N
n51
1
2n 2 1
18.
X
N
n51
1
n 1
ffiffiffi
n
p
19.
X
N
n52
1
lnðnÞ
20.
X
N
n51
1 1 lnðnÞ
3n 2 2
21.
X
N
n51
2n 1 5
n
2
1 1
22.
X
N
n51
n 1 2
2n
3=2
1 3
23.
X
N
n51
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
10 1 n
2
p
24.
X
N
n51
2 1 sinðnÞ
ffiffiffi
n
p
25.
X
N
n51
3
n
1 1
3
n
1 2
n
26.
X
N
n51
2
n
n
2
27.
X
N
n51
3
n
1 n
ffiffiffi
n
p
3
n
1 1
28.
X
N
n51
2
n
1 1
2
n
1 n
2
c In Exercises 29248, use the Limit Comparison Test to
determine whether the given series converges or diverges. b
29.
X
N
n51
3n
2n
2
2 1
30.
X
N
n51
ffiffiffiffiffiffiffiffiffiffiffi
n 1 1
p
n
2
31.
X
N
n51
ffiffiffiffiffiffiffiffiffiffiffiffiffi
n
2
1 1
p
n
2
32.
X
N
n51
ðn 2 1Þ
2
ðn 1 1Þ
4
33.
X
N
n51
10n 1 3
100n
3
2 99
34.
X
N
n51
n
2
1 2
ðn
2
1 1Þ
2
35.
X
N
n51
ffiffiffi
n
p
1 1
2n
2
2 n
36.
X
N
n51
3
2
n
1 3
37.
X
N
n51
2
n
1 11
3
n
2 1
8.3 The Comparison Tests 659
38.
X
N
n51
arctanðnÞ
n
2
39.
X
N
n51
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 n
2
p
ð1 1 n
8
Þ
1=4
40.
X
N
n51
n
1=3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 n
5=2
p
41.
X
N
n51
2
n
1 1 2
2n
42.
P
N
n51
sinð1=nÞ
43.
X
N
n51
sinð1=nÞ
n
44.
X
N
n51
n 1 lnðnÞ
n
3
45.
X
N
n51
1
n 1 lnðnÞ
46.
X
N
n51
2
n
1 n
3
3
n
1 n
2
47.
X
N
n51
7
n
10
n
1 n
10
48.
X
N
n51
2n 1 5
3n 1 7
n
Further Theory and Practice
c In each of Exercises 492 72, use a Comparison Test to
determine whether the given series converges or diverges. b
49.
X
N
n51
2n 1 1
n
2
50.
X
N
n51
2 1 sinðnÞ
ffiffiffi
n
p
51.
X
N
n51
n 1 2
2n
3=2
1 3
52.
X
N
n51
5
n
1 6
7
n
53.
X
N
n51
n 1 2
n
2
1 1
2
54.
X
N
n51
ffiffiffiffiffiffiffiffiffiffiffiffiffi
n 1 2
n
3
1 1
r
55.
X
N
n51
1 1 1=n
n
56.
X
N
n51
lnðn
3
Þ
n
3
57.
X
N
n52
n
lnðnÞ
3
58.
X
N
n51
arctanðnÞ
n
59.
X
N
n51
100
n
n
n
60.
X
N
n51
tanð1=nÞ
n
61.
P
N
n51
sinð1=n
2
Þ
62.
P
N
n51
1 2 cosð1=nÞ
63.
X
N
n51
1
2
2
1
3n
n
64.
X
N
n51
2
5
1
sinðnÞ
3
n
65.
X
N
n51
2
n
1 3
n
7
n
1 5
n
66.
P
N
n51
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sinð1=n
3
Þ
p
67.
X
N
n51
n
3
ðn
3
1 n
2
1 1Þ
2
68.
X
N
n51
4
n
2
12
3n 1 1
69.
P
N
n51
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
4
1 2
ffiffiffi
n
p
p
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
4
1
ffiffiffi
n
p
p
70.
X
N
n51
sec
1
ffiffiffi
n
p
2 cos
1
ffiffiffi
n
p
71.
X
N
n52
ffiffiffiffiffiffiffiffiffiffiffiffiffi
n
2
1 1
p
nlnðnÞ
2
72.
X
N
n52
1 1 lnðn
2
Þ
lnðn
4
Þ
n
73. Let
P
N
n51
a
n
and
P
N
n51
b
n
be series of positive terms.
Suppose that lim
n-N
a
n
=b
n
5 0. Show that if
P
N
n51
b
n
converges, then
P
N
n51
a
n
also converges.
74. Let
P
N
n51
a
n
and
P
N
n51
b
n
be series of positive terms.
Suppose that lim
n-N
a
n
=b
n
5 N. Show that if
P
N
n51
b
n
diverges, then
P
N
n51
a
n
also diverges.
75. Suppose that {a
n
} is a sequence of positive numbers.
Show that if
P
N
n51
a
n
converges, then
P
N
n51
a
2
n
also
converges.
76. Suppose that {a
n
} and {c
n
} are sequences of positive
numbers. Suppose that c
n
- ‘ where ‘ is a real number.
Show that if
P
N
n51
a
n
converges, then
P
N
n51
a
n
c
n
also
converges.
77. Let p be any number. Show that
P
N
n51
n
p
r
n
is convergent
if 0 , r , 1.
78. Let q be any number. Show that
P
N
n51
ln
q
ðnÞ=n
p
is con-
vergent if 1 , p.
79. Show that
P
N
n51
n!=n
n
is convergent.
660 Chapter 8 Infinite Series
Calculator/Computer Exercises
80. Let S 5
P
N
n51
lnðnÞ
n
1=3
n
. A brute-force computer calcu-
lation shows that the 1000
th
partial sum satisifes
S
1000
5 941.010575563 .... As a consequence of limit for-
mula (8.3.1), there is a positive integer M such that
lnðnÞ
n
1=3
, 0:9 for n $ M . Find this value of M, and obtain an
upper bound S
M21
1
P
N
n5M
ð0:9Þ
n
for S.
81. Find a positive integer M such that n
10
0.99
n
, 0.995
n
for all
n $ M. Prove that the series
P
N
n51
n
10
0:99
n
is convergent.
8.4 Alternating Series
In this section, we study series with terms that alternate between positive and
negative values. Because the partial sums of such series do not form an increasing
sequence, the Integral Test and the Comparison Tests do not apply. In this section,
we will develop a different test for handling these so-called alternating series.
The Alternating
Series Test
The idea of cancellation motivates the next convergence test, which is concerned
with the series we consider in this section. These series have alternating signs ( . . . ,
1, 2 ,1, 2, . . . ), and are called alternating series. It is convenient to account for the
sign changes by writing the series in the form
P
N
n51
ð21Þ
n21
a
n
5 a
1
2 a
2
1 a
3
2 :::
where 0 , a
n
for all n. If instead, the signs of the even terms are positive, then we
write the series as
P
N
n51
ð21Þ
n
a
n
52a
1
1 a
2
2 a
3
1 where 0 , a
n
for all n.
Because this last series is just the negative of
P
N
n51
ð21Þ
n21
a
n
, each statement that
we make about one of the series will hold for the other.
THEOREM 1
(Alternating Series Test) Let fa
n
} be a sequence of nonnegative
numbers that satisfy the following two cond itions:
a. a
1
$ a
2
$ a
3
$ ...
b. lim
n-N
a
n
5 0
Then
P
N
n51
ð21Þ
n21
a
n
converges. Furthermore, the limit ‘ 5
P
N
n51
ð21Þ
n21
a
n
lies
between each pair of consecutive partial sums S
N
5
P
N
n51
ð21Þ
n21
a
n
and
S
N11
5 S
N
1 (21)
N
a
N11
. In particular, the limit ‘ satisfies the inequality
j‘ 2 S
N
j# a
N11
: ð8:4:1Þ
Proof. First
observe that
S
1
5 a
1
$ a
1
1 ð2a
2
1 a
3
Þ5 S
3
$ a
1
1 ð2a
2
1 a
3
Þ1 ð2a
4
1 a
5
Þ5 S
5
$ a
1
1 ð2a
2
1 a
3
Þ1 ð2a
4
1 a
5
Þ1 ð2a
6
1 a
7
Þ5 S
7
::::
Therefore the odd partial sums form a decreasing sequence. In a similar way, we
see that the even partial sums form an increasing sequence. The sequence of even
partial sums lies to the left of the sequence of odd partial sums (see Figure 1).
S
2
0
S
4
S
6
S
5
a
5
a
4
a
3
a
2
a
1
S
3
S
1
m Figure 1
8.4 Alternating Series 661

Therefore the two monotone sequences are bounded, hence convergent. Let ‘
denote the limit of the odd partial sums. For any positive integer N, S
2N
2 S
2N21
5
a
2N
- 0. Hence the even and odd partial sums tend to the same limit ‘. This means
that the series converges. Because ‘ lies between each pair of consecutive partial
sums S
N
and S
N
1 a
N11
, inequality (8.4.1) follows. ’
Some Examples The Alternating Series Test applies to series in which the terms (1) have alternating
signs and (2) decrease in absolute value to 0. Always be sure to verify these
hypotheses when applying the test.
⁄ EX
AMPLE 1 Apply Theorem 1 to the series
X
N
n51
ð21Þ
n21
1
n
:
Solution Set a
n
5 1/n. Then, a
1
$ a
2
$ a
3
$ . . . and a
n
- 0. Thus the series has the
form of an alternating series as in Theorem 1. The Alternating Series Test applies,
and
P
N
n51
ð21Þ
n21
=n converges. ¥
INSIGHT
Notice that if we remove the minus signs from the series in Example 1,
then we obtain the harmonic series, which is divergent. The minus signs cause enough
cancellation to occur so that the series converges. Theorem 1 does not tell us the value ‘
of
P
N
n51
ð21Þ
n21
=n, but it does allow us to make an estimate. If we want to evaluate ‘
with an error less than 0.01, then we find the first index n for which 1/n , 0.01. This value
is 101. By inequality (8.4.1), we can be sure that
‘ 2
X
100
n51
ð21Þ
n21
=n
#
1
101
, 0:01:
With a computer, we can calculate
P
100
n51
ð21Þ
n21
=n 0:6882. This number is our
approximation. In fact, it is known that
P
N
n51
ð21Þ
n21
=n is exactly equal to ln(2), or
0.693 ....
⁄ EXAMPLE 2 Analyze the series
X
N
n51
ð21Þ
n
1
ffiffiffi
n
p
.
Solution Because a
n
5 1=
ffiffiffi
n
p
decreases to 0, the Alternating Series Test may be
applied to the series
P
N
n51
ð21Þ
n21
=
ffiffiffi
n
p
, which is the negative of the given series.
Therefore the original series also converges.
¥
⁄ EXAMPLE 3 Does the series
X
N
n51
ð21Þ
n
1
1 1 1=n
converge?
Solution The
given series is indeed alternating. However, the terms do not tend to
0. Therefore the Alternating Series Test does not apply; we may draw no
conclusion from that test. However, the Divergence Test does apply; it tells us that
the series diverges because the terms do not tend to 0.
¥
Because the first terms of a series do not affect convergence, we may be able to
deduce that a series converges by applying the Alternating Series Test to an
appropriate tail. The next example illustrates this idea.
662 Chapter 8 Infinite Series

⁄ EXAMPLE 4 Show that the series
X
N
n51
ð21Þ
n21
lnðn
4
Þ
ffiffiffi
n
p
converges.
Solution A
plot of ln(x
4
)/
ffiffiffi
x
p
(Figure 2) indicates that this expression is not
decreasing for all positive x, but it does appear to decrease from some point
forward. To be sure, we differentiate the expression. We find that
d
dx
lnðx
4
Þ
ffiffiffi
x
p
5 4
d
dx
lnðxÞ
x
1=2
5 4
x
1=2
x
21
2
1
2
x
21=2
lnðxÞ
x
5 2
2 2 lnð x Þ
x
3=2
:
This expression is negative for ln(x) . 2, or x . e
2
7.39. It follows that the
sequence a
n
5 ln(n
4
)/
ffiffiffi
n
p
decreases for n $ 8. Also notice that
lim
n-N
a
n
5 lim
n-N
lnðn
4
Þ
ffiffiffi
n
p
5 4 lim
n-N
lnðnÞ
n
1=2
5
ð8:3:1Þ
0:
Thus the Alternating Series Test does apply to the tail series
P
N
n58
ð21Þ
n21
lnðn
4
Þ=
ffiffiffi
n
p
. Because the tail converges, the full series also converges.
Absolute Convergence It is useful to distinguish between series that converge because of cancellation and
series that converge because of size. Then we can learn something by comparing
the two. These considerations motivate the following definition.
DEFINITION
Let
P
N
n51
a
n
be a series, possibly containing terms of both positive
and negative sign. If the series
P
N
n51
ja
n
j of absolute values converges, then we
say that the series
P
N
n51
a
n
converges absolutely.
⁄ EX
AMPLE 5 Does the series
P
N
n51
ð21Þ
n21
=n converge absolutely?
Solution The
given series converges by the Alternating Series Test, as noted in
Example 1. But the series
P
N
n51
jð21Þ
n21
=nj is the harmonic series,
P
N
n51
1=n, which
diverges. Therefore the series
P
N
n51
ð21Þ
n21
=n does not converge absolutely. ¥
⁄ EXAMPLE 6 Does the series
P
N
n51
ð21=2Þ
n
converge? Does it converge
absolutely?
Solution The
given series is a geometric series with ratio 21/2, which is less than 1
in absolute value. Therefore it is convergent. For the same reason, the series of
absolute values,
P
N
n51
jð21=2Þ
n
j5
P
N
n51
ð1=2Þ
n
, converges. Therefore the given
series converges absolutely.
¥
INSIGHT
Our intuition tells us that absolute convergence is “better” than ordinary
convergence. Example 5 suggests that it is harder for a series to converge absolutely than
it is for a series to simply converge. By making the even-indexed terms of the divergent
3.0
1.0
2.0
50
10 20 30 40
x
y
ln(x
4
)
x
y
冑
m Figure 2
8.4 Alternating Series 663

series 1 1 1/2 1 1/3 1 1/4 1 negative, the resulting series 1 2 1/2 1 1/3 2 1/4 1
converges thanks to the partial cancellation among consecutive terms with opposite signs.
By contrast, an absolutely convergent series converges without this aid. The next theo-
rem makes this intuition substantive.
THEOREM 2
If the series
P
N
n51
ja
n
j converges, then the series
P
N
n51
a
n
con-
verges. In other words, absolute convergence implies convergence.
Proof. Let b
n
5 a
n
1 ja
n
j. Then, 0 # b
n
# 2ja
n
j. By hypothesis,
P
N
n51
ja
n
j converges
so that
P
N
n51
2ja
n
j converges. Using the Comparison Test for Convergence, we
conclude that
P
N
n51
b
n
also converge s. However, a
n
5 b
n
2ja
n
j. By Theorem 2a of
Section 1, we conclude that
P
N
n51
a
n
converges, as required. ’
⁄ EXAMPLE 7 Test the series
X
N
n51
sinðnÞ
2
n
for convergence.
Solution Notice
that sin(n) is sometimes positive and sometimes negative, but it
does not alternate in sign. The pattern of signs begins 1 , 1 , 1 ,2,2,2, 1 ,
1 , 1 ,2,2,2 . . . , but the pattern is less simple than these initial terms suggest:
sin(22), sin(23), sin(24), sin(25) produce four consecut ive negative terms. Therefore
the Alternating Series Test cannot be used. The Comparison and Integral Tests do
not apply because the series has both positive and ne gative terms. In short, not one
of the tests for convergence that we have learned in previous sections can be
applied to the given series. But we can apply the Comparison Test for Convergence
to the series
P
N
n51
jsinðnÞ=2
n
j of absolute values. We have 0 # jsin(n)/2
n
j# 1/2
n
, and
because
P
N
n51
1=2
n
is a convergent geometric series, we can conclude that
P
N
n51
jsinðnÞ=2
n
j converges. Theor em 2 then tells us that the original series
P
N
n51
sinðnÞ=2
n
converges. ¥
The sum of tw o different absolutely convergent series remains absolutely
convergent. To see why, suppose that
P
N
n50
a
n
and
P
N
n50
b
n
are absolutely con-
vergent. Notice that ja
n
1 b
n
j# ja
n
j1 jb
n
j for each index n by the triangle
inequality. Therefore
X
N
n51
ja
n
1 b
n
j#
X
N
n51
ja
n
j1
X
N
n51
jb
n
j#
X
N
n51
ja
n
j1
X
N
n51
jb
n
j, N:
It follows that the partial sums of the series
P
N
n51
ja
n
1 b
n
j are bounded and that the
series is convergent. We record this and some other simple facts as the following
theorem.
THEOREM 3
Let
P
N
n50
a
n
and
P
N
n50
b
n
be absolutely convergent series. Then,
a.
P
N
n50
ða
n
1 b
n
Þ and
P
N
n50
ða
n
2 b
n
Þ are absolutely convergent.
b.
P
N
n50
λ a
n
converges absolutely for any real constant λ.
664 Chapter 8 Infinite Series
