Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Theorem 2 does not tell us the value of a convergent series

n51

but it

is extremely useful nonetheless. Until now, we have had to ﬁnd an explicit

formula for the partial sum S

in order to determine the convergence of

n51

Theorem 2 allows us to determine convergence with less precise information about

the partial sums. Here is an example of how Theorem 2 can be used.

⁄ EX

AMPLE 3 Discuss convergence for the series

n51

1=n

Solution The

summands 1/n

are all positive. Theorem 2 tells us that

n51

1=n

convergent if there is a real number U such that S

# U for all N. In fact, U 5 3/2

will do:

5 1 1

1 1

# 1 1

1 1



1 1

1 1



n50





5 2 2

by equation ð8:1:13Þwith r 5 1=2:

To recapitulate, the inﬁnite series

n51

1=n

is co nvergent because its terms are

positive and its partial sums are bounded above.

INSIGHT

In Example 3, we are able to conclude that the inﬁnite series

n51

1=n

converges without actually ﬁnding its sum ‘. Because our analysis shows that S

# 3/2 for

all N, we deduce that

n51

1=n

5 lim

N-N

# 3=2. If we need a more precise estimate,

then we must calculate partial sums. Using a computer, we calculate S

5 1.291285997

(to ten signiﬁcant digits) and S

5 1.291285997 as well. With a little more calculation,

we see that adding more terms changes only those digits that are beyond the ninth

decimal place.

⁄ EXAMPLE 4 Give an example of a divergent inﬁni te series

n51

whose

partial sums S

n51

are bounded.

Solution Acco

rding to Theorem 2, the summands a

cannot all be nonne gative. In

fact, we have already encountered an inﬁnite series that has the properties we seek:

n51

ð21Þ

. We have observed that the partial sums of this series are all either 21

or 0 (Section 8.1, Example 5) and the series diverges (Section 8.1, Example 8). The

lesson is that the hypothesis a

$ 0 cannot be omitted from Theorem 2. ¥

The Tail End of a Series Whether or not a given series converges does not depend on the ﬁrst million or so

terms. For suppose that we are given the series

n51

and that we are able to

ascertain that

n510

converges. This means that there is a real number ‘ such

that lim

N-N

n510

5 ‘. But this limit allows us to see that the partial sums of

the full series converge :

8.2 The Divergence Test and the Integral Test 645

lim

N-N

n51

5 lim

N-N



n51

n510



n51

1 lim

N-N

n510

n51

1 ‘:

Of course, there is nothing special about the number 10

.IfM is any positive

integer, then we refer to

n5M11

as a tail of

n51

. The full series

n51

convergent if and only if the tail

n5M11

is convergent. In this case, the two

inﬁnite series

n51

and

n5M11

differ only by the partial sum

n51

which, comprising ﬁnitely many summands, is ﬁnite.

⁄ EX

AMPLE 5 Let a

5 1/2

n 2 1

if n , 1000, and a

5 1/n for n $ 1000. Does

the series

n51

converge?

Solution The

series must diverge. For if

n51

were convergent, then the tail

n51000

,or

n51000

1=n, would be convergent. But this tail of

n51

is also a

tail of

n51

1=n. The convergence of

n51000

1=n would therefore imply the

convergence of

n51

1=n. That is false (Section 8.1, Theorem 1). ¥

⁄ EXAMPLE 6 Does the series

n510

nðn 1 1Þ

converge? If so, to what

number?

Solution Yes:

the given series is a tail of the convergent series

n51

nðn 1 1Þ

(Section 8.1, Example 9), and so it too is convergent. The difference between the

series

n51

nðn 1 1Þ

and the given series is just the ﬁnite sum

n51

nðn 1 1Þ

, which

we calcu late to be 9/10. Because we know that

n51

nðn 1 1Þ

5 1 from Example 9

of Section 8.1, we see that

n510

nðn 1 1Þ

n51

nðn 1 1Þ

n51

nðn 1 1Þ

5 1 2

: ¥

The Integral Test We have already noted the analogy between inﬁnite series and improper integrals

over an inﬁnite interval. We develop that idea further to obtain a convergence test

for inﬁnite series of positive terms.

THEOREM 3

(The Integral Test) Let f be a positive, continuous, decreasing

function on the interval [1,N). Then the inﬁnite series

n51

f ðnÞ converges if

and only if the improper integral

f ðxÞdx converges. In this case, we have

f ðxÞdx #

n51

f ðnÞ# f ð1Þ1

f ðxÞdx: ð8:2:1Þ

Proof. Look

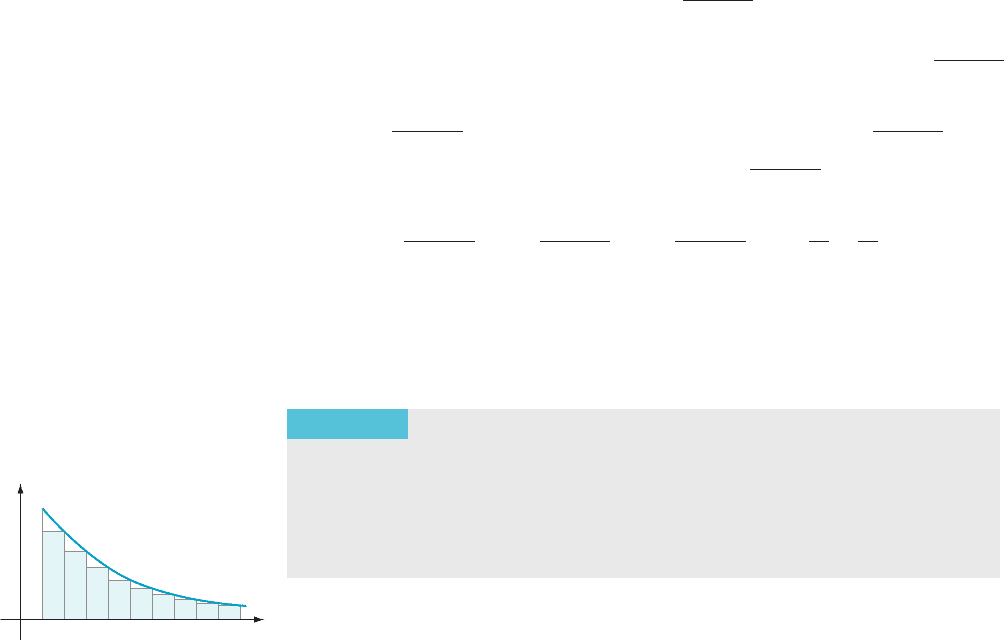
at Figure 1. Because the base of each inscribed rectangle has length 1,

the area of each rectangle is equal to its height. Thus the area of the ﬁrst rectangle

is f (2), the area of the second box is f (3), and so on. All the boxes lie under the

graph. Therefore

n52

f ðnÞ#

f ðxÞdx: ð8:2:2Þ

12345

. . .



y  f(x)

f(2)

f(3)

f(4)

m Figure 1 The area of the

shaded rectangles is the series

n52

f ðnÞ.

646 Chapter 8 Inﬁnite Series

If the improper integral

f ðxÞdx is convergent, then the numbers

f ðxÞdx

increase to a (ﬁnite) limit as N tends to inﬁnity. This limit is denoted by

f ðxÞdx.

Using inequality (8.2.2) we deduce that

n51

f ðnÞ5 f ð1Þ1

n52

f ðnÞ# f ð1Þ1

f ðxÞdx # f ð1Þ1

f ðxÞdx:

Thus the pa rtial sums of

n51

f ðnÞ are bounded above by f (1) 1

f ðxÞdx, and, as

a result, the series

n51

f ðnÞ is convergent and bounded above by

f (1) 1

f ðxÞdx.

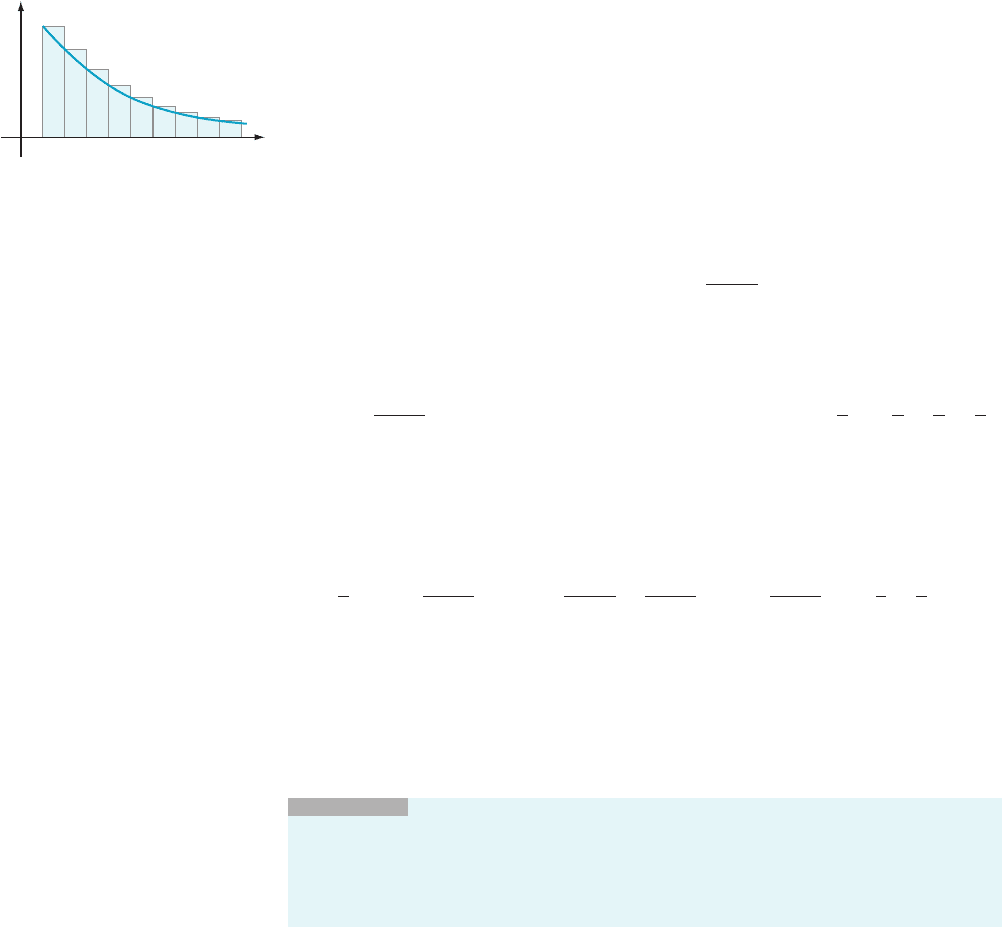
Now look at the superscribed rectangles in Figure 2. Clearly

f ðxÞdx #

N21

n51

f ðnÞ: ð8:2:3Þ

n51

f ðnÞ is convergent, then inequality (8.2.3) tells us that the numbers

f ðxÞdx are bounded above by

n51

f ðnÞ. As a result,

f ðxÞdx is convergent

and bounded above by

n51

f ðnÞ. ’

The crux of the proof of the Integral Test is in the geometry. Remember the

pictures,

and you will remember why the test works. Here are several examples.

⁄ EX

AMPLE 7 Show that the series

n51

1 1 n

converges, and estimate its

value

Solution We

apply the Integral Test to the continuous, positive, decreasing

function f (x) 5 1/(1 1 x

). Because

f ðxÞdx 5

1 1 x

dx 5 lim

N-N

arctanðxÞ



x5N

x51

5 lim

N-N



arctanðNÞ2



;

we conclude that

f ðxÞdx is convergent. According to the Integral Test, the

series

n51

f ðnÞ5

n51

1=ð1 1 n

Þ is also converge nt. The Integral Test also

provides an estimate of the value of the series. Because

1=ð1 1 x

Þdx 5 π=4, line

(8.2.1) tells us that

0:785 

1 1 x

dx #

n51

1 1 n

1 1 1

1 1 x

dx 5

 1:285:

In fact, a computer calculation shows that

n51

1=ð1 1 n

Þ5 1:076 :::, which is

indeed in the interval [0.785 , 1.285] that we determined. It is sometimes useful to

have such estimates even when they are not particularly accurate. For the series of

Example 7, we can improve on the lower bound 0.785 obtained from the Integral

Test by simply summing three terms

n51

1=ð1 1 n

Þ5 4=5 5 0:8. ¥

INSIGHT

The Integral Test is stated in terms of a function f. In practice, we apply

the Integral Test when presented with an inﬁnite series

n51

. Example 7 shows how to

deﬁne an appropriate function f starting from the series: In the expression for a

, replace

the summation index n with x, and the formula for f (x) results. Of course, before

applying the Integral Test, we must be sure that f is positive, continuous, and decreasing.

12345

. . .



f(1)

f(2)

f(3)

m Figure 2 The area of the

shaded rectangles is the series

N21

n51

f ðnÞ.

8.2 The Divergence Test and the Integral Test 647

⁄ EXAMPLE 8 Show that the series

n51

converges, and estimate its value.

Solution The

function f (x) 5 x/e

is positive, continuous, and decreasing for x $ 1

because for these values of x, we have f uðxÞ5 ðe

2 xe

Þ=e

5 ð1 2 xÞ=e

# 0. Next,

we will investigate the improper integral of f (x). We have, by an application of

integration by parts with u 5 x and dv 5 e

dx,

f ðxÞdx 5 lim

N-N

dx 5 lim

N-N

ð2xe



x5N

x51

5 lim

N-N

ð2 xe

2 e



x5N

x51

Therefore

f ðxÞdx 5 lim

N-N

ð2Ne

2 e

Þ2 ð2e

2 e

Þ52 lim

N-N

;

where we have used Example 3 of Section 8.1 to conclude that lim

N-N

5 0.

Because

f ðxÞdx converges and equals 2/e, it follows from the Integral Test that

n51

n=e

also converges. Line (8.2.1) tells us that

0:7358 

dx #

n51

dx 5

 1:1036:

Using more advanced techniques, it can be shown that the value of the given series

is e/(e 2 1)

5 0.92067 . . . , which indeed lies between our lower and upper

estimates.

INSIGHT

The limit formula

lim

x-N

λx

5 0 ð0 , λÞ; ð8:2:4Þ

which holds for any constant p, is frequently useful. For p 5 1, equation (8.2.4) is

proved by applying l’Ho

pital’s Rule, as in Example 3 of Section 8.1. In general, equation

(8.2.4) is proved by repeatedly applying l’Ho

pital’s Rule.

p-Series If p is a ﬁxed number then the inﬁnite series

n51

1=n

is called a p-series. Our next

theorem comple tely describes how the convergence of the p-series depends on the

value of p.

THEOREM 4

Fix a real number p. The series

n51

converges if 1 , p; it

diverges if p # 1.

Proof. If p is

not positive, then the terms of the series do not tend to 0. According

to the Divergence Test, the series must diverge. If p is positive, then f (x) 5 1/x

positive, continuous, and decreasing on the interval [1,N). We may therefore apply

the Integral Test. There are three cases to consider. If 0 , p , 1, then

dx 5 lim

N-N

1 2 p

 x

12p



5 N:

648 Chapter 8 Inﬁnite Series

The Integral Test tells us that the series diverges. If p 5 1, then the series

n51

1=n

is the harmonic series, which diverges. (The Integral Test can also be used to

demonstrate this divergence). Finally, if p . 1, then

dx 5 lim

N-N

dx 5 lim

N-N

12p



1 2 p

lim

N-N



p21

2 1



p 2 1

The Integral Test then tells us that the series converge s. ’

⁄ EX

AMPLE 9 Determine whether

n51

n 1 2

3=2

is convergent.

Solution Th

e series

n51

1=n

3=2

is a p-series with p 5 3/2 . 1. Therefore it is

convergent. If the given series were convergent, then Theorem 2 of Section 8.1 (with

5 (n 1 2)/n

3/2

, b

5 1/n

3/2

,andλ 522) would tell us that

n51

ða

1 2b

Þ5

n51



n 1 2

3=2

2 2

3=2



n51

3=2

n51

1=2

is convergent. But

n51

1=n

1=2

is a p-series with p 5 1/2 # 1. Therefore it is

divergent. We conclude that the given series must be divergent; otherwise, we would

have a contradiction.

An Extension It is often convenient and sometimes necessary to apply the Integral Test with an

initial summation index M greater than 1. We ﬁrst apply the Integral Tes t to see

that

n5M

and

f ðxÞdx have the same con vergence behavior. Then we note

that the full series

n51

shares the behavior of its tail.

THEOREM 5

Suppose that f is a positive, continuous, decreasing function on

the interval [M,N). Let fa

} be a sequ ence with a

5 f (n) for all n with M # n.

Then, the inﬁnite series

n51

converges if and only if the improper integral

f ðxÞdx converges.

⁄ EX

AMPLE 10 Determine whether the series

n52

nlnðnÞ

converges.

Solution Th

is series begins with n 5 2; notice that the summand is not even deﬁned

for n 5 1. Because x and ln(x) are increasing functions of x, so is the product x ln(x).

The reciprocal f (x) 5 1/(x ln(x)) of this product is therefore decreasing. Because f

is also positive and continuous on the interval [2,N) we may apply the Integral Test.

Using the substitution u 5 ln(x), du 5 (1/x)dx, we calculate

f ðxÞdx 5 lim

N-N

xlnðxÞ

dx 5 lim

N-N

lnðNÞ

lnð2Þ

du 5 lim

N-N

lnðjujÞ



u5lnðNÞ

u5lnð2Þ

5 lim

N-N





lnðNÞ



2 ln



lnð2Þ





5 N:

The divergence of the improper integral

f ðxÞdx implies the divergence of the

inﬁnite series

n52

f ðnÞ5

n52



n lnðnÞ



. ¥

8.2 The Divergence Test and the Integral Test 649

⁄ EXAMPLE 11 Use the Integral Test to show that the series

n51

2n=10

converges.

Solution The

given series is equal to

n51

f ðnÞ for f (x) 5 x

2x/10

. In this case,

f has an increasing factor, namely x

. To apply the Integral Test, we must be sure

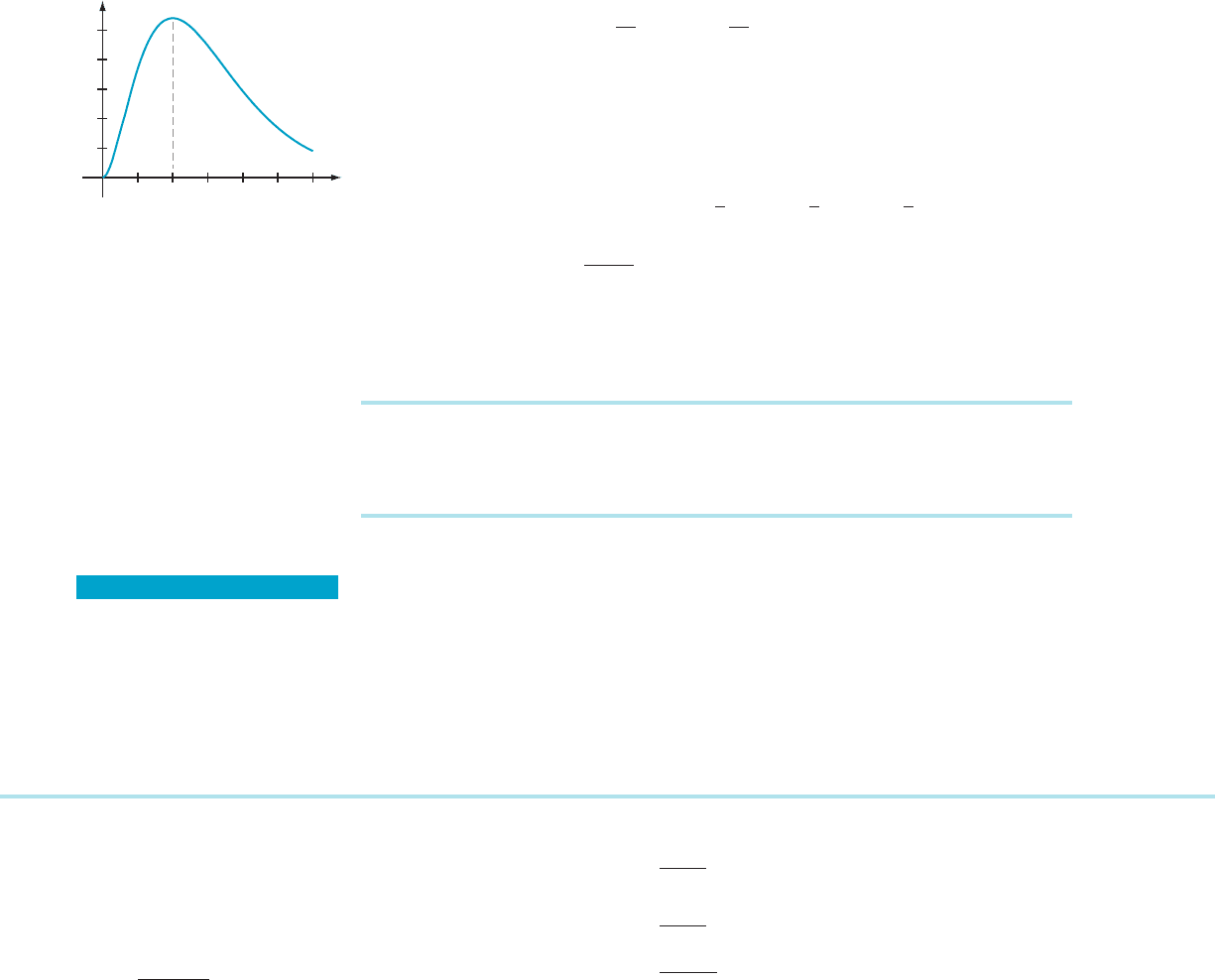
that f itself is decreasing. The plot of f in Figure 3 suggests that f (x) increases for

x , 20 and decreases for 20 , x. We can conﬁrm this last observation by showing

that f uðxÞ, 0 for 20 , x:

f uðxÞ5 2xe

2x=10

1 x





2x=10

ð20 2 xÞ, 0 for 20 , x:

We may therefore apply the Integral Test over the interval [20,N). By integrating

by parts twice and using equation (8.2.4) with both p 5 2 and p 5 1, we calculate

f ðxÞdx 5 lim

N-N

2x=10

5 lim

N-N



210x

2200xe

22000e





x5N

x520

10000

It follows that

f ðxÞdx is convergent, and, as a result,

n520

f ðnÞ is con-

vergent. Therefore

n51

2n=10

n51

f ðnÞ5

n51

f ðnÞ1

n520

f ðnÞ is also

convergent.

b A LOOK BACK The Integral Test works by comparing the partial sums of a series

with the area under a curve. It is often natural to compare the partial sums of one

series with those of a series whose convergence is known. The next section is

devoted to this powerful technique.

QUICK QUIZ

1. True or false:

n51

ﬃﬃﬃ

converges because lim

n-N

ð1=

ﬃﬃﬃ

Þ5 0.

2. True or false: The Divergence Test cannot be applied to the series

n51

1=n

3. True or false:

n51

1=n

3=2

converges.

4. True or false: A series with bounded partial sums is convergent.

Answers

1. False 2. True 3. True 4. False

5010 20 30 40

f (x)  x

x兾10

m Figure 3

EXERCISES

Problems for Practice

c In Exercises 1220, state what conclusion, if any, may be

drawn from the Divergence Test. b

n51

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

ﬃﬃﬃ

n51

1 1

n51

1 4

n51

1 1 1=n

650 Chapter 8 Inﬁnite Series

n51

lnðnÞ

n51

1 3

n51

1 1 lnðnÞ

n51

1 5

10.

n51

1 3

11.

n51

1 1

1 n

12.

n51

1=4

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

ﬃﬃﬃ

13.

n51

1 1

14.

n51

1 n 1 1

15.

n51

1=n

16.

n51

17.

n51



π=2 2 arctanðnÞ



18.

n51

cosð1=nÞ

19.

n51

sinð1=nÞ

20.

n51



n=ðn 1 1Þ2 1=ðn 1 2Þ



c In each sentence in Exercises 21226, use either the word

“may”

or the word “must” to ﬁll in the blank so that the

completed sentence is correct. Explain your answer by

referring to a theorem or example. b

21. A

series with summands tending to 0__converge.

22. A series that converges __ have summands that tend to 0.

23. If a series diverges, then the Divergence Test __ succeed

in proving the divergence.

24. If the partial sums of an inﬁnite series are bounded, then

the series __ converge.

25. If a series diverges, then its terms __ diverge.

26. If the partial sums of an inﬁnite series diverge, then the

series __ diverge.

c In each of Exercises 272 46, use the Integral Test to

determine

whether the given series converges or diverges.

Before you apply the test, be sure that the hypotheses are

satisﬁed. b

27.

n51

28.

n51

1 1

29.

n51

1 4

30.

n51

nðn 1 2Þ

31.

n51

n 1 3

32.

n51

33.

n51

1 4

34.

n52

n lnðnÞ

35.

n51

ðn 1 3Þ

5=4

36.

n52

2 n

37.

n58

ð1 1 e

38.

n51

39.

n52

1 n

40.

n54

nln

ðnÞ

41.

n51

lnðnÞ

42.

n51

1 2n 1 1

43.

n51

22n

44.

n51

45.

n52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

46.

n53

nln

3=2

ðnÞ

c In each of Exercises 47254, use known facts about p-s

eries

to determine whether the given series converges or diverges. b

47.

n51

ﬃﬃﬃ

48.

n51

ðπ2eÞ

49.

n51

ﬃﬃﬃ

ﬃﬃ

50.

n51

7n 2

ﬃﬃﬃ

51.

n51

ﬃﬃﬃ

1 5

8.2 The Divergence Test and the Integral Test 651

52.

n51

1 1

53.

n51

1 11

54.

n51

1=8

1 3n

1=16

1 1

5=4

Further Theory and Practice

c In Exercises 55268, state what conclusion, if any, may be

drawn from theDivergence Test. b

55.

n51





1=n

56.

n51



sinð1=nÞ2 1=n



57.

n51

ð1 1 1=nÞ

58.

n51



cosð1=nÞ2 secð1=nÞ



59.

n51

lnðn

60.

n51

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 3

2 nÞ

61.

n51



ð111=nÞ

2 n



62.

n51

sinðnÞ

63.

n51

nsinð1=nÞ

64.

n51

ðn!Þ

ð2nÞ!

65.

n51

arctanðnÞ

66.

n51

tanðπ=3 2 1=nÞ

67.

n51



arcsecðnÞ2 arctanðnÞ



68.

n51



n 2 1



c In Exercises 69274, use the Integral Test to determine

whether the given series converges. b

69.

n51

70.

n51

lnðnÞ

71.

n51

1 1 n

1=2

72.

n51



n 1 3



73.

n51



1 1



74.

n51

arctanðnÞ

1 1 n

c In each of Exercises 75278, verify that the given function f

satisﬁes the hypotheses of the Integral Test and that

f ðxÞdx is convergent. Use line (8.2.1) to ﬁnd an interval in

which

n51

f ðnÞ lies. b

75. f (x) 5 x/(3 1 x

)

5/2

76. f (x) 5 x

/(1 1 x

)

77. f ðxÞ5

expðxÞ



1 1 expðxÞ



78. f ðxÞ5

expðxÞ

1 1 expð2xÞ

79. Show that

n51

ð1=2Þ

is convergent.

80. Derive the inequality

ﬃﬃﬃ

, 1=2

, which holds for

every positive integer n. Prove that the inﬁnite series

n51

ﬃﬃﬃ

is convergent by showing that its partial sums

are bounded by 1.

81. Notice that

n! 5 n ðn 2 1Þ:::4  3  2  1 . 2  2:::2  2  2  1

for n $ 3. Use this observation to ﬁnd a number U that is

an upper bound of the inﬁnite series

n51

1=n! (thereby

showing that this series is convergent).

82. Determine whether

n52

dx converges.

83. Determine whether

n52

dx converges.

84. Use the Integral Test to prove that the series

n520

nlnðnÞln



lnðnÞ



diverges.

85. Deﬁne f (x) 5 sin

(πx) 1 1/x

for x $ 1. Notice that f is

positive and continuous. Show that

f ðxÞdx diverges,

yet

n51

f ðnÞ converges. Explain why the conclusion of

the Integral Test is not valid.

86. For which values of p is

n51



1 1



convergent?

87. Let {d

} be a sequence of positive numbers. Let

5 min (d

/2, 1/2

). Show that

n51

converges.

88. Prove that if 0 # a

and

n51

converges then there exist

numbers b

with a

, b

such that

n51

still converges.

89. Prove that if 0 . c

and

n51

diverges, then there exist

numbers d

satisfying 0 , d

, c

and such that

n51

diverges. This exercise shows that there is no “largest

convergent series” and no “smallest divergent series.”

c Let H

n51

1=n denote the partial sums of the har-

monic series. Let A

5 H

2 ln(N). Exercises 90293 establish

that lim

N-N

exists. This important number, usually

denoted by γ, is called the Euler-Mascheroni constant. Its

value is 0.5772156649 to ten decimal places. b

90. Sketch y 5 1/x.

Use the ideas of the Integral Test to

illustrate the geometric signiﬁcance of A

. Draw a

652 Chapter 8 Inﬁnite Series

staircase-shaped region whose area is H

. Shade the

region (comprising N 2 1 “triangular” regions and one

rectangle) whose area is A

91. Let a

denote the area of the “triangular” region above

y 5 1/x, below y 5 1/n, and between x 5 n and x 5 n 1 1.

Your sketch should show that

N21

n51

By comparison with a circumscribed rectangle, show that

0 , a



n 1 1



92. Show that the partial sums of the series

n51

are

bounded by the value of the convergent series

n51



n 1 1



5 1:

Deduce that the limit γ 5 lim

N-N

exists and is a

number between 1/2 and 1.

93. This exercise presents an alternative, analytic approach to

the limit lim

N-N

. Let f ( x) 5 x 1 ln(1 2 x) for 0 # x , 1.

Show that f uðxÞ, 0 for 0 , x , 1. Deduce that f (x) , 0 for

0 , x , 1. Show that A

N11

2 A

5 f (1/(N 1 1)). Deduce

that {A

} is a positive decreasing sequence, hence

convergent.

94. Suppose {a

} and f satisfy the hypotheses of the Extended

Integral Test (Theorem 5). Show that

M21

n51

f ðxÞdx #

n51

and

n51

f ðxÞdx:

Use these estimates together with the integral formula

2x=4

dx 5 e

2M=4

ð4M

1 32M 1 128Þ to ﬁnd an

interval in which

n51

2n=4

lies.

Calculator/Computer Exercises

c Suppose that f is positive, continuous, and decreasing on

[1,N). Let

LðMÞ5

M21

n51

f ðnÞ1

f ðxÞdx

and

UðMÞ5 f ðMÞ1 LðMÞ:

Then, according to the result of Exercise 94,

LðMÞ,

n51

f ðnÞ, UðMÞ:

c In each of Exercises 95298, for the given function f,

cal-

culate the least value M such that U(M)2L(M) , 5 3 10

State

n51

f ðnÞ to three decimal places. b

95. f (x) 5 1/x

96. f ðxÞ5

ðx 1 1Þ

97. f (x) 5 x/(3 1 x

)

5/2

98. f (x) 5 x

/(1 1 x

)

8.3 The Comparison Tests

In the preceding section, we studied the convergence of a series

n51

of non-

negative terms by comparing the series wi th an improper integral. The idea was to

show the boundedness of the increasing sequence of partial sums. In this section,

we will see that the same goal can often be reached by comparing the given inﬁnite

series with another series.

The Comparison Test

for Convergence

Suppose that

n51

is a convergent series of nonnegative terms with

n51

5 ‘.

Because the partial sums

n51

form an increasing sequence, these partial sums

must increase to ‘. In particular, each partial sum satisﬁes

n51

# ‘.If

n51

another series satisfying 0 # a

# b

for every n, then the partial sums for this series

satisfy

n51

# ‘:

8.3 The Comparison Tests 653

Thus the partial sums of the series

n51

are increasing (because the a

’s are

nonnegative) and bounded above by ‘. By the Monotone Convergence Property

(Section 2.6 in Chapter 2), we conclude that the sequence of partial sums of

n51

converge. We summarize in the following theorem.

THEOREM 1

(The Comparison Test for Convergence) Let 0 # a

# b

for

every n. If the series

n51

converges, then the series

n51

also converges.

⁄ EX

AMPLE 1 Show that the series

n51

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ

converges.

Solution Observe

that

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ5 n

ﬃﬃﬃ

1 n 1

ﬃﬃﬃ

. n

ﬃﬃﬃ

5 n

3=2

for every

positive n. We conclude that

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ

3=2

for every positive n. Also,

n51

1=n

3=2

is a p-series that is convergent (because p 5 3/2 . 1). By the

Comparison Test for Convergence, the given series

n51

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ

converges.

INSIGHT

When the Comparison Test for Convergence is applied to a series

n51

,asecond series

n51

must be found. How does one go about ﬁnding such a

series for comparison? In Example 1, look at the denominator

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ,orn

3/2

n 1 n

1/2

, of the general term of the series. Compare the contribution of each summand to

the total. When n is 10,000, for instance, the term n

3/2

, which is 1,000,000, is comparable

to n

3/2

1 n 1 n

1/2

, which is 1,010,100. This sort of rounding is encountered all the time in

the reporting of sales ﬁgures or economic data. In summary, discarding all but the largest

power of n in the denominator of

ﬃﬃﬃ

ðn 1

ﬃﬃﬃ

1 1Þ

results in the simpler expression 1/n

3/2

which is the comparison used in Example 1.

⁄ EXAMPLE 2 Discuss convergence for the series

n51

ð3n 2 2Þ

Solution Notice

that 3n 2 2 5 n 1 2(n 2 1) $ n for all n $ 1. Therefore

(3n 2 2)

$ n

so that 1/(3n 2 2)

# 1/n

. Finally,

n51

1=n

is a convergent p-

series (with p 5 2 . 1). By the Comparison Test for Convergence, we conclude that

n51

1=ð3n 2 2Þ

converges. ¥

INSIGHT

It is often possible to come to an intuitive decision about the convergence

of a series without doing a precise comparison. In Example 2, we see that for large n, the

summand 1/(3n 2 2)

is about the same size as 1/(3n)

. Such a rough comparison is

enough for us to predict the convergence of

n51

1=ð3n22Þ

by comparison with

(1/9)

n51

1=n

. The Limit Comparison Test, which will appear later in this section, will

make this idea precise.

⁄ EXAMPLE 3 Discuss convergence for the series

n51

sin

ð2n 1 5Þ

1 8n 1 6

654 Chapter 8 Inﬁnite Series