Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

by comparison with the convergent geometric series

n50

. In summary, we have

proved that if a power series

n50

converges at some value of x, then it

converges absolutely at all points that have a smaller absolute value. It follows that

the set of points where the series converges is an interval centered at the origin.

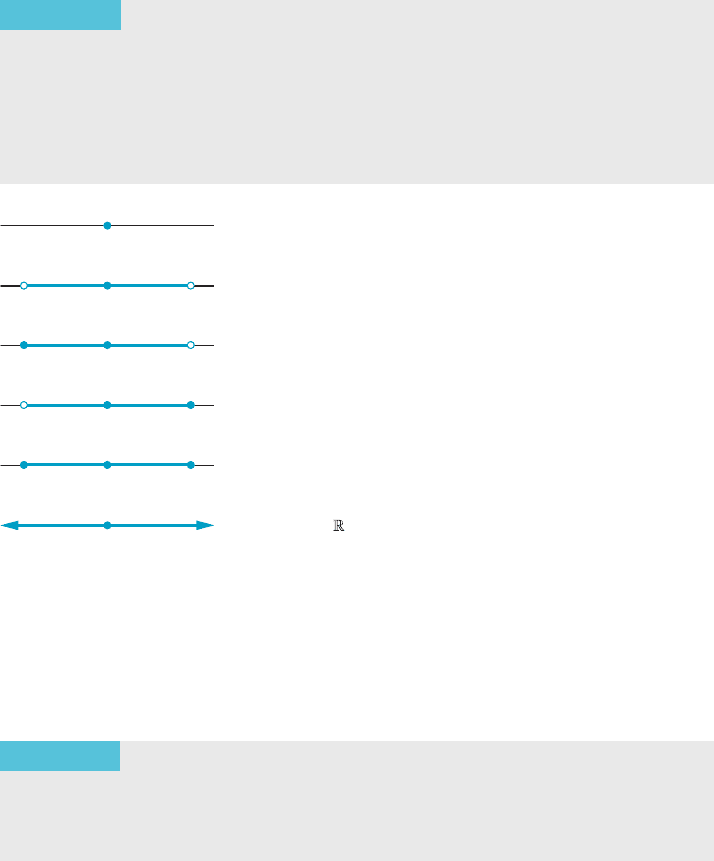
This interval can have inﬁnite length, ﬁnite positive length, or zero length (see

Figure 1). We state this as the following theorem.

THEOREM 1

Let

n50

be a power series. Then precisely one of the fol-

lowing statements holds:

a. The series converges absolutely for every real x.

b. There is a positive number R such that the series converges absolutely for

jxj, R and diverges for jxj. R.

c. The series converges only at x 5 0.

Whichever the case, there is a quantity R that is either a nonnegative real

number or 1N such that the power series

n50

converges absolutely for

jxj, R and diverges for jxj. R. In case a of Theorem 1, R 5Nand in case c, R 5 0.

In all cases, we say that R is the radius of convergence of the power series. We now

learn how to compute this quantity.

THEOREM 2

Suppose that the limit ‘ 5 lim

n-N

1=n

exists (as a nonnegative

real number orN). Let R denote the radius of convergence of the power series

n50

.If0, ‘ ,N, then R 5 1/‘.If‘ 5 0, then R 5N, and if ‘ 5N, then

R 5 0.

Proof. The

Root Test (Section 8.5) applied to

n50

tells us the series converges

absolutely when L 5 lim

n-N

1=n

, 1 and diverges when L 5 lim

n-N

1=n

. 1.

Notice that L 5 jx jlim

n-N

1=n

5 jxj‘. Thus the series converges absolutely for

jxj‘ , 1 ð8:6:1Þ

0 RR

Single point {0}

Open interval (R, R)

Left-closed, right-open interval [R, R)

Left-open, right-closed interval (R, R]

Closed interval [R, R]

Entire real line

0 RR

m Figure 1 Intervals of convergence.

8.6 Introduction to Power Series 675

and diverges for

jxj‘ . 1: ð8:6:2Þ

If ‘ 5 0, then inequality (8.6.1) is satisﬁed for all x. Consequently R equalsN.If‘ 5N,

then inequality (8.6.2) is satisﬁed for all x 6¼0, and therefore R 5 0. If ‘ is ﬁnite an d

positive, then the series converges for jxj, 1/‘ and diverges for jxj. 1/‘. This means

that R 5 1/‘. ’

DEFINITION

The set of points at which a power series

n51

converges is

called the interval of convergence.

If R 5N, then the interval of convergence is the entire real line. If R 5 0, then

the interval of convergence is the single point {0}. When 0 , R ,N, the series

converges on the interval (2R, R) but it may or may not conve rge at the endpoints

x 5 R and x 52R. To determine the interval of convergence, each endpoint must

be tested separately by substituting the values x 5 R and x 52R into the series.

Thus when R is positive and ﬁnite, the interval of convergence will have the form

[2R, R]or(2R, R]or[2R, R)or(2R, R), as shown earlier in Figure 1.

⁄ EX

AMPLE 3 Find the interval of convergence for the power series

n50





Solution With a

5 1/3

, we calculate

‘ 5 lim

n-N

1=n

5 lim

n-N





1=n



5 lim

n-N

The radius of convergence R is the reciprocal of ‘. Thus R 5 3. This tells us that the

series converges (absolutely) when j x j, 3 and diverges when jxj. 3. To completely

determine the interval of convergence, we must investigate each endpoint. When

x 5 3, the series becomes

n50

1, which diverges. When x 523, the series becomes

n50

ð21Þ

, which also diverges. The interval of convergence is therefore (23, 3).

As a function of x, the domain of the power series

n50

is the open interval

(23, 3).

⁄ EXAMPLE 4 Find the interval of convergence for the series

n51

=n.

Solution We

set a

5 1/n and calculate

‘ 5 lim

n-N

1=n

5 lim

n-N



1=n

5 lim

n-N

1=n

ð8:5:1Þ

The radius of convergence R is given by R 5 1/‘ 5 1. Thus the series converges

(absolutely) for jxj, 1 and diverges when jxj. 1. When x 5 1 the series becomes

n51

1=n; this is the harmonic series, which diverges. When x 521, the series

becomes

n51

ð21Þ

=n, which is convergent by the Alternating Series Test. We

conclude that the interval of convergence is [21, 1). The power series

n51

deﬁnes a function of x with domain [21, 1).

676 Chapter

8 Inﬁnite Series

INSIGHT

We know from Theorem 1 that convergence is absolute at any point of the

interval of convergence other than an endpoint. Nevertheless, the deﬁnition of “interval

of convergence” refers only to convergence—not absolute convergence. If R 2(0,N)is

the radius of convergence of a power series

n50

and if the series converges when

x 5 R, then R is in the interval of convergence whether the convergence is conditional or

absolute. The same statement holds for 2R. Thus in Example 4, the endpoint 21 belongs

to the interval of convergence of

n51

=n even though

n51

=n converges con-

ditionally when x 521.

⁄ EXAMPLE 5 Find the radius and interval of convergence for the power

series

n51

 n

Solution Let a

5 1/(5

 n

). Then the radius of convergence R is given by

R 5



lim

n-N

1=n





lim

n-N



 n



1=n





lim

n-N

5  n

2=n



5 5 lim

n-N

ðn

1=n

ð8:5:1Þ

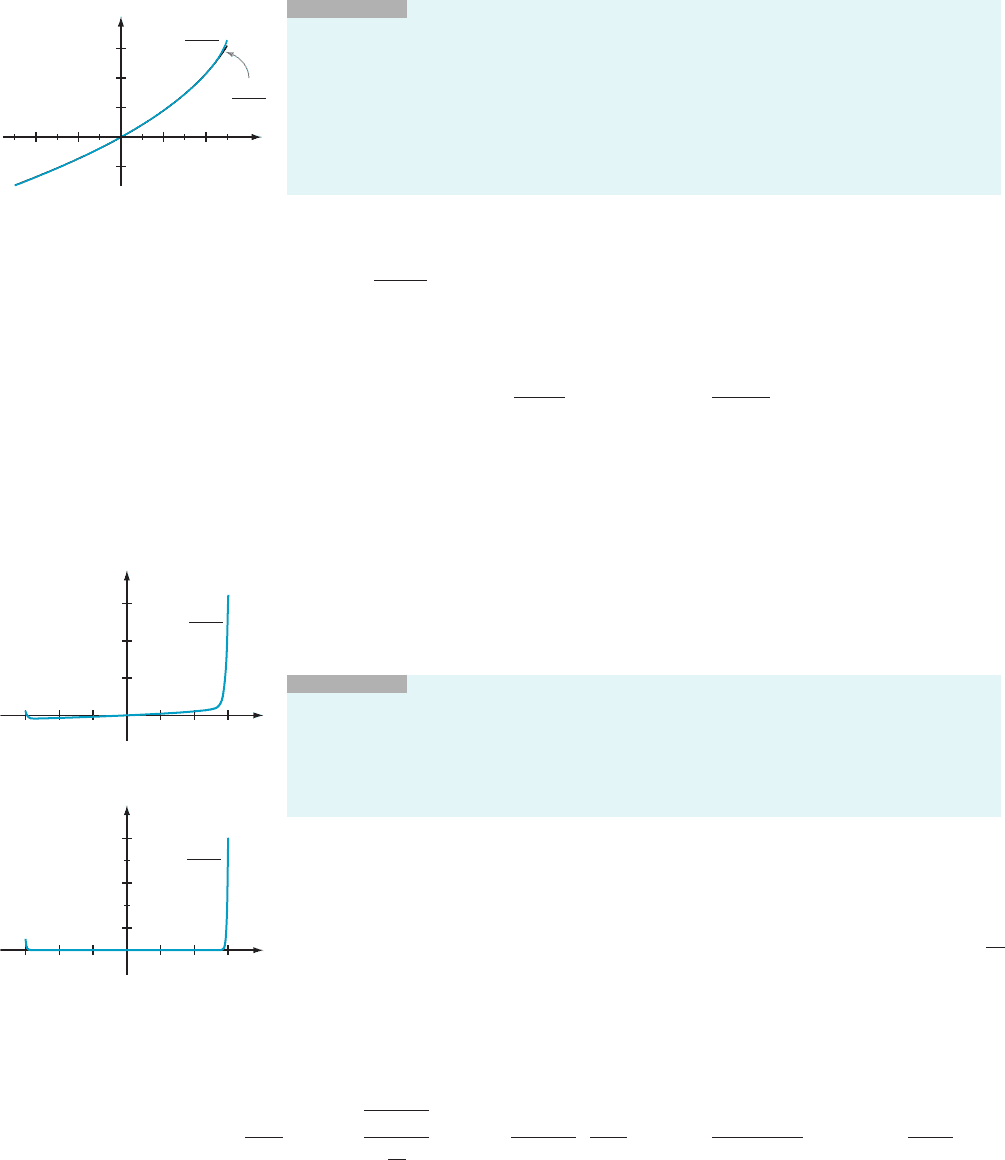
Thus the series converges (absolutely) when jxj, 5 and diverges when jxj. 5.

When x 5 5, the series becomes

n51

1=n

, which is a convergent p-series. When

x 525, the series becomes

n51

ð21Þ

, which, by the Alternating Series Test,

also converges. We conclude that the interval of convergence is [25, 5]. The power

series

n51

=ð5

 n

Þ therefore deﬁnes a function with domain [25, 5]. This

function is plotted in Figure 2. The graph of the approximating partial sum,

n51

=ð5

 n

Þ, is also shown in the ﬁgure. The approximating curve and the

original curve are so close that they are difﬁcult to distinguish.

INSIGHT

Graphing some partial sums of a power series can provide clues to its

convergence properties. Example 5 shows that [25, 5] is the interval of convergence of

n51

=ð5

 n

Þ. Figure 3 suggests the divergence outside this interval. In Figure 3a, the

partial sum

n51

=ð5

 n

Þ is plotted over the interval [26, 6]. In Figure 3b, the partial

sum

100

n51

=ð5

 n

Þ is plotted. Notice the scales on the vertical axes.

Sometimes it is convenient to use the Ratio Test when calculating the radius of

convergence. The next example will illustrate this technique.

⁄ EX

AMPLE 6 Find the interval of convergence for the power series

n50

by using the Ratio Test.

Solution Acco

rding to the Ratio Test (Section 8.5), the series

n51

converges

absolutely if lim

n-N

n11

j, 1 and diverges if lim

n-N

n11

j. 1. We set

5 x

/n! and calculate

lim

n-N



n11



5 lim

n-N

n11

ðn 1 1Þ !



5 lim

n-N



ðn 1 1Þ!



n11



5 lim

n-N



ðn 1 1Þn!

 x



5 lim

n-N



n 1 1



5 0:

1.5

1.0

0.5

244

0.5





n  1



n  1

m Figure 2

66442

2



n  1

m Figure 3a

66442

10000

30000

50000

2



100

n  1

m Figure 3b

8.6 Introduction to Power Series 677

In particular, the limit is always less than 1. Hence, the Ratio Test tells us that the

series converges absolutely for every real x. In other words, R 5N, and the interval

of convergence is (2N,N).

INSIGHT

Remember that a ratio of factorials can be simpliﬁed by peeling off factors

from the larger factorial until both numerator and denominator involve the same

factorial (which is then canceled). Example 6 illustrates this technique, as does the

next example.

⁄ EXAMPLE 7 Find the radius and interval of convergence for the series

n51

ð2nÞ!

Solution We

set u

5 (2n)!x

/n! and calculate

lim

n-N



n11



5 lim

n-N

ð2n 1 2Þ!

ðn 1 1Þ!

n11

ð2nÞ!



5 lim

n-N



ð2n 1 2Þ!

ð2nÞ!



ðn 1 1Þ !

 x



Because (n 1 1)! 5 (n 1 1) n! and (2n 1 2)! 5 (2 n 1 2)(2n 1 1) (2n)!, we have

lim

n-N



n11



5 lim

n-N



ð2n 1 2Þð2n 1 1Þð2nÞ!

ð2nÞ!



ðn 1 1Þn!

 x



5 lim

n-N



ð2n 1 2Þð2n 1 1Þ

ðn 1 1Þ

 x



5 lim

n-N

j2ð2n 1 1Þ x j:

This limit is less than 1 only when x 5 0. It exceeds 1 (in fact the limit is inﬁnite) for

any nonzero value of x. Therefore R 5 0, and the interval of conv ergence is the set

{0} that contains only the origin.

The calculations that we have performed in Examples 6 and 7 can be gen-

eralized to yield another formula for the radius of convergence. We state this

formula now and indicate its derivation in Exercise 65.

THEOREM 3

Let R be the radius of convergence of the power series

n50

Suppose that

‘ 5 lim

n-N

n11

exists (as a nonnegative real number or N). If 0 , ‘ ,N, then R 5 1/‘.If‘ 5 0,

then R 5N.If‘ 5N, then R 5 0.

INSIGHT

Each of Theorems 2 and 3 gives a formula for the radius of convergence.

Which should be used? Naturally, when both limits exist, they must have the same value.

In courses on Advanced Calculus, it is shown that, of the two, the formula based on

the Root Test has wider scope. However, the formula based on the Ratio Test is

frequently easier to calculate. Therefore the Ratio Test is often tried ﬁrst.

678 Chapter 8 Inﬁnite Series

Power Series about an

Arbitrary Base Point

Often, it is useful to consider series that consist of powers of the form (x 2 c)

where c is any ﬁxed constant. These series will have a radius of convergence R just

as before, but now the interval of convergence will be centered at the base point c.

(Until now, we have considered only power series centered at 0.) We will still have

to test the endpoints separately to determine the exact interval of convergence.

DEFINITION

Suppose that {a

} is a sequence of constants and that c is a real

number. An expression of the form

S 5 a

1 a

ðx 2 c Þ1 a

ðx 2 cÞ

1 a

ðx 2 cÞ

1 

is called a power series in x with base point (or center) c.

It is convenient to denote the constant term a

of S by a

(x 2 c)

so that we may

write S as

n50

ðx 2 cÞ

. Notice that a power series with base point 0 is exactly

the sort of power series with which we have already been working. The next

theorem expresses the content of Theorems 1, 2, and 3 for an arbitrary base point.

THEOREM 4

Let fa

n50

be a sequence for which ‘ 5 lim

n-N

1=n

exists as a

nonnegative real number or N. Then ‘ is also given by the formula

‘ 5 lim

n-N

n11

, if this limit exists. If 0 , ‘ ,N, set R 5 1/‘.If‘ 5 0, set R 5N.

If ‘ 5N, set R 5 0. Then

n50

ðx 2 cÞ

converges absolutely for fjx 2 cj, R }

and diverges for jx 2 cj. R. In particular, if R 5 N, then the series converges

absolutely for every real x.IfR 5 0, then the series converges only at x 5 c.

As with the case in which c 5 0, we call R the radius of convergence of the

power series. The set on which the series converges is called the interval of con-

vergence.IfR 5N, then the interval of convergence is the entire real line. If R 5 0,

then the interval of convergence is the single point {c}. When 0 , R ,N, the series

may or may not converge at the endpoints x 5 c 2 R and x 5 c 1 R. To determine

the interval of convergence, each endpoint must be tested separately by sub-

stituting the values x 5 c 2 R and x 5 c 1 R into the series. Thus when R is positive

and ﬁnite, the interval of conve rgence will have the form [c 2 R, c 1 R]or(c 2 R,

c 1 R]o

r[c 2 R, c 1 R)or(c 2 R, c 1 R). Figure 4 illustrates the possibilities.

⁄ EX

AMPLE 8 Calculate the interval of convergence for the power series

n50

ðx 2 2Þ

Solution Becau

n50

ðx 2 2Þ

n50

ðx 2 2Þ

with a

5 1 for all n,we

calculate ‘ 5 lim

n-N

1=n

5 lim

n-N

1=n

5 1: We set R 5 1/‘ 5 1. Theorem 4 tells

us that the series converges (absolutely) for every x that satisﬁes jx 2 2j, 1and

diverges for every x such that jx 2 2j. 1. The points x 5 2 1 1 5 3 and x 5 2 2 1 5 1

must be tested separately. When x 5 3, the series becomes

n50

, which diver ges.

When x 5 1, the series becomes

n50

ð21Þ

, which also diverges. Thus the interval

of convergence is the open interval (1, 3).

8.6 Introduction to Power Series 679

The ﬁnal example involves several elemen ts of calculating the inte rval of

convergence of a power series. We ﬁrst enumerate the steps.

Steps for Calculat ing an Interval of Convergence

1. Write the power series in the standard form

n50

ðx 2 cÞ

. In particular, the coefﬁcient of x in the power

(x 2 c)

should be 1, and the base point c should be subtracted from x. To complete step 1, identify the center

c of the interval of convergence and the coefﬁcient a

2. Calcul ate ‘ 5 lim

n-N

1=n

or ‘ 5 lim

n-N

n11

j. To complete step 2, identify the radius of convergence

If ‘ 5 0, then R 5N, and the interval of convergence is (2N,N). If ‘ 5N, then R 5 0, and the interval of

convergence is {0}. In both of these cases, the calculation is complete. If 0 , ‘ ,N, then R 5 1/‘. Steps 3 and 4

are necessary in this case.

3. Substitute x 5 c 2 R in

n50

ðx 2 cÞ

and determine the convergence of the resulting series,

n50

ð21Þ

. At the conclusion of this step, it will be known if the interval of convergence does or does not

contain its left endpoint c 2 R.

4. Substitute x 5 c 1 R in

n50

ðx 2 cÞ

, and determine the convergence of the resultin g series,

n50

At the conclusion of this step, it will be known if the interval of convergence does or does not contain its

right endpoint c 1 R.

⁄ EX

AMPLE 9 Determine the interval of convergence of the series

n50

ð21Þ

5n 1 1

ð2x 1 5Þ

Solution The

ﬁrst step is to write this power series in the standard form

n50

ðx 2 cÞ

. We have

n50

ð21Þ

ð2x 1 5Þ

5n 1 1

n50

ð21Þ

5n 1 1



x 1



n50

ð22Þ

5n 1 1



x 2





Now we can identify the base point c 525/2 and the coefﬁcients a

5 (22)

(5n 1 1). For step 2, we calculate

c  R

c  R

c  R

c  R

c  R

c  R

Single point {c}

Open interval (c  R, c  R)

Left-closed, right-open interval

[c  R, c  R)

Left-open, right-closed interval

(c  R, c  R]

Closed interval [c  R, c  R]

Entire real line

0 c  Rc  R

m Figure 4 Intervals of convergence centered at c.

680 Chapter 8 Inﬁnite Series

‘ 5 lim

n-N

n11

5 lim

n-N



ð22Þ

n11

5ðn 1 1Þ1 1



ð22Þ

5n 1 1



5 lim

n-N

ð5n 1 1Þ2

n11

ð5n 1 6Þ2

5 2 lim

n-N

5n 1 1

5n 1 6

5 2 lim

n-N

5 1 1=n

5 1 6=n

5 2:

Therefore R 5 1/‘ 5 1/2. The endpoints of the interval of convergence are

c 2 R 525/2 2 1/2 523andc 1 R 525/2 1 1/2 522. When x 523, the series

becomes

n50

1=ð5n 1 1Þ, which diverges by the Integral Test (or by the Limit

Comparison Test using the harmonic series for comparison). At this point, the end

of step 3, we know that the interval of convergence is either (23,22) or (23,22].

When x 522, the series becomes

n50

ð21Þ

=ð5n 1 1 Þ, which converges by the

Alternating Series Test. Therefore the interval of convergence is (23,2 2].

Addition and Scalar

Multiplication of

Power Series

The ﬁrst result tells us how to add or subtract two power series with the same base

point and how to multiply a power series by a scalar. It is a straightforward

application of Theorem 3, Section 9.5 of Chapter 9.

THEOREM 5

Let λ be any real number. Suppose that

n50

ðx 2 cÞ

and

n50

ðx 2 c Þ

are power series that converge absolutely on an open interval I.

Then

a. The power series

n50

ða

1 b

Þðx 2 cÞ

and

n50

ða

2 b

Þðx 2 cÞ

also

converge absolutely on I; moreover,

n50

ðx 2 cÞ

n50

ðx 2 cÞ

n50

ða

1 b

Þðx 2 cÞ

and

n50

ðx 2 cÞ

n50

ðx 2 cÞ

n50

ða

2 b

Þðx 2 cÞ

b. The power series

n50

λa

ðx 2 c Þ

converges absolutely on I and

n50

ðx 2 cÞ

n50

λ a

ðx 2 c Þ

⁄ EX

AMPLE 10 On what open interval does

n50



5 2



ðx22Þ

converge?

Solution The

series

n50

ð1=3Þ

has radius of convergence 3 (as shown in

Example 3). Because the calculation of a radius of convergence depends only on the

coefﬁcients {a

}of

n50

ðx 2 cÞ

and not on the center, it follows that

n50

ð1=3Þ

ðx 2 2Þ

also has radius of convergence 3. Therefore

n50

ð1=3Þ

ðx 2 2Þ

converges absolutely when x is in (2 2 3, 2 1 3), or (21, 5). By Example 8, the series

n50

ðx 2 2Þ

converges absolutely when x 2(1, 3). Therefore by Theorem 5b, so

does the series

n50

5ðx 2 2Þ

. By Theorem 5a,

n50



5 2 ð1=3Þ



ðx 2 2Þ

is equal

8.6 Introduction to Power Series 681

to the difference

n50

5ðx 2 2Þ

n50

ð1=3Þ

ðx 2 2Þ

and converges absolutely

on the intersection (1, 3) of the two intervals.

Differentiation and

Antidifferentiation of

Power Series

A function that has derivatives of all orders on an open interval is said to be

inﬁnitely differentiable. The next theorem says that a power series that converges

on an open interval is inﬁnitely differentiable. Furthermore, the power series may

be differentiated termwise and integrated termwise.

THEOREM 6

Suppose that a power series

n50

ðx 2 cÞ

has a positive radius

of converge nce R. Let I denote the interval (c 2 R, c 1 R) and deﬁne a function f

on I by f ðxÞ5

n50

ðx 2 cÞ

. Then,

a. The function f is inﬁnitely differentiable on I and

f uðxÞ5

n51

ðx 2 cÞ

n21

The power series for f u has radius of convergence R.

b. The power series

FðxÞ5

n50

n 1 1

ðx 2 cÞ

n11

has radius of convergence R. The function F satisﬁes the equation Fð x Þ5

f ðtÞdt for all x in I. In particular, FuðxÞ5 f ðxÞ on I. The indeﬁnite integral

of f (x) is given by

f ðxÞdx 5 FðxÞ1 C where C is an arbitrary constant.

⁄ EX

AMPLE 11 Calculate the derivative and the indeﬁnite integral of the

power series f ðxÞ5

n51

ﬃﬃﬃ

 x

for x in the interval of convergence I 5 (21, 1).

Solution By

Theorem 6a, f uðxÞ5

n51

ﬃﬃﬃ

n21

for x in I. Although this formula

correctly represents f uðxÞ as a power series, we generally prefer to express a power

series in standard form (in which the power of the variable is equal to the index of

summation). If we change the index of summation by setting m 5 n 2 1, then as n

ranges over the integers from 1 to N, m ranges over the integers from 0 to N, and

f uðxÞ5

m50

ðm 1 1Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

m 1 1

Also, according to Theorem 6, the indeﬁnite integral of f (x)i

f ðxÞdx 5

n51



ﬃﬃﬃ

n 1 1



n11

1 C:

To write this power series in standard form, we change the index of summation to

m 5 n 1 1. Then, as n ranges over the integers from 1 to inﬁnity, m ranges over the

integers from 2 to inﬁnity, and

f ðxÞdx 5 C 1

m52

 ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

m 2 1



: ¥

682 Chapter 8 Inﬁnite Series

INSIGHT

If we explicitly write out several terms of f (x), f uðxÞ, and

f ðxÞ dx, then

our term-by-term differentiation and integration becomes more evident:

f ðxÞ 5 x 1

ﬃﬃﬃ

1 

;

f uðxÞ 5 1 1 2

ﬃﬃﬃ

x 1 3

ﬃﬃﬃ

1 

;

f ðxÞdx 5 C 1

ﬃﬃﬃ

1 

QUICK QUIZ

1. True or false: If lim

n-N



n11



5 2, then the radius of convergence of

n50

is 2.

2. True or false: If lim

n-N

1=n

5 2, then the radius of convergence of

n50

is 1/2.

3. What is the center of the interval of convergence of

n50

ð3x 1 2 Þ

=n!?

4. If f ðxÞ5

n50

=ðn 1 2Þ, what is the coefﬁcient of x

in the power series for

f uðxÞ?

Answers

1. False 2. True 3. 22/3

4. 5/7

EXERCISES

Problems for Practice

c In Exercises 1210, use Theorem 2 and, where necessary,

limit formula (8.5.1) to calculate the radius of convergence R.

Determine the interval of convergence I by checking the

endpoints. b

n50

ð2xÞ

n50





n51

n50

ðn 1 1Þ

n51

ð21Þ

n11

n51

ð4xÞ

n50



2nx

3n 1 1



n51

10.

n51





c In Exercises 11220, use Theorem 3 to calculate the radius

of convergence R. Determine the interval of convergence I by

checking the endpoints. b

11.

n50

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

12.

n50

13.

n50

1 1

 x

14.

n53

3n 1 5

n 2 2

 x

15.

n50

1 1

16.

n50

1 1 2

1 1 3

 x

17.

n50

ð21Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

18.

n51

ð21Þ

n11

ﬃﬃﬃ

 10

19.

n52

lnðnÞ

20.

n50

ð2xÞ

8.6 Introduction to Power Series 683

c In each of Exercises 21230, use Theorem 4 to calculate the

radius of convergence R. Determine the interval of con-

vergence I by checking the endpoints. b

21.

n51

ðx 1 6Þ

ﬃﬃﬃ

22.

n51

ðπ 2 xÞ

23.

n50

ðx 1 4Þ

1 1

24.

n50

ðx 2 3Þ

2n 1 3

25.

n50

ð2x 1 1Þ

26.

n50

ð3x 1 2Þ

n 1

ﬃﬃﬃ

1 1

27.

n50

ð21Þ

n 1 1

3n 1 1

ðx 1 5Þ

28.

n50





29.

n51



x 1 1



30.

n50

1 n



x 1



c In each of Exercises 31234, ﬁnd the open interval on

which the given power series converges absolutely. b

31.

n50

ð2

2 2

Þðx 2 1Þ

32.

n51





ðx 1 1Þ

33.

n50

ð3

1 2

Þðx 1 2Þ

34.

n50





ðx 2 3Þ

c In each of Exercises 35238, the given power series

n50

ðx 2 cÞ

deﬁnes a function f. State the partial sum

n50

ðx 2 cÞ

of the power series for f uðxÞ, and determine

the interval I of convergence of f uðxÞ. b

35.

n51

36.

n51

37.

n51

ðx 2 1Þ

3=2

38.

n51



x 1



c In each of Exercises 39242, the given power series

n50

ðx 2 cÞ

deﬁnes a function f. Calculate the partial sum

n51

ðx 2 cÞ

of the power series for FðxÞ5

f ðtÞdt, and

determine the interval I of convergence of F(x). b

39.

n50

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

40.

n50

n 1 1

41.

n50

ðx 2 2Þ

42.

n50

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n 1 1

ðx 1 2Þ

Further Theory and Practice

c In each of Exercises 43248, ﬁnd the radius of convergence

of the given power series. b

43.

n50

nðn 1 1Þðn 1 2Þð2x 1 3Þ

44.

n51

ð1=n 2 1=2

Þðx 1 1Þ

45.

n51

ðn!Þ

ð2nÞ!

46.

n51



n 1 1



47.

n51

ðn! Þ

ðn

Þ!

ðnxÞ

48.

n50

ð2

c Each power series in Exercises 49252, comprises only

even powers (x 2 c)

. Make the substitution t 5 (x 2 c)

, ﬁnd

the interval of convergence of the series in t, and use it to ﬁnd

the interval of convergence of the original series. b

49.

n50

ð21Þ

ðx 1 1Þ

50.

n51

ðx 1 3Þ

51.

n50

ð2x 2 1Þ

52.

n51

n ð3xÞ

c Each power series in Exercises 53256 comprises only odd

powers (x 2 c)

2n11

. Factor out (x 2 c)

to produce a series

consisting of even powers. Follow the instructions to Exercises

49252 to ﬁnd the interval of convergence of the given series. b

53.

n51

ð2xÞ

2n11

=ðn 1 1Þ

54.

n51

nðx 2 1Þ

2n11

=25

55.

n50

ðx 1 eÞ

2n11

56.

n50

ðx 1

ﬃﬃﬃ

2n11

c Suppose that α and β are positive real numbers with α , β.

In each of Exercises 57260, ﬁnd a power series whose interval

convergence is precisely the given interval. b

57. (α, β)

58. (α, β]

684 Chapter

8 Inﬁnite Series