Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

GENESIS

DEVELOPMENT7

Archimedes and the Sphere

Arc lengths, surface areas, and volumes—these con-

cepts were all investigated by the geometers of ancient

Greece. Archimedes, for example, demonstrated that

the volume enclosed by a sphere is 2/3 the volume

of the circumscribing cylinder and that the surface area

of a sphere is (also) 2/3 the area of the cir cumscribing

cylinder (including its circular ends). Stated more

explicitly, he proved that the volume and surface area

of a sphere of radius r are 4πr

/3 and 4π r

, respectively.

These results must have pleased Archimedes, for

he requested that his tomb be decorated with a sphere

and cylinder and that the ratio giving their relationship

be inscribed. His wishes were carried out, as we learn

from Cicero, who in 75

B.C. rediscovered and repaired

the overgrown, forgot ten site:

“I remembered some verses which I had been

informed were engraved on his monument, and

these set forth that on the top of the tomb there was

placed a sphere with a cylinder. . . . I observed a

small column standing out a little above the briers

with the ﬁgure of a sphere and a cylinder upon it . . .

When we could get at it. . . . I found the inscription,

though the latter parts of all the verses were almost

half effaced. Thus one of the noblest cities of

Greece, and one which at one time likewise had

been very celebrated for learning, had known

nothing of the monument of its greatest genius . . . .”

The restored grave of Archimedes eventually van-

ished again. However, in modern times, workers exca-

vating the site of a hotel in Syracuse reported coming

upon a stone tablet inscribed with a sphere and a cylinder.

Kepler and Solids of Revolution

In 1612, Johannes Kepler (15711630) took up residence

in Linz. As the wine harvest was good that year, the

Danube River banks were ﬁlled with wine casks. “This

being so,” in the words of Kepler’s biographer, Max

Caspar, “as husband and good pater-familias,hecon-

sidered it his duty to provide his home with the necessary

drink.” Accordingly, Kepler had some wine barrels

installed in his house. After seeing a wine merchant esti-

mate the volume of a cask by simply inserting a measuring

stick, Kepler set himself the problem of deve loping a more

scientiﬁc system of calculating volumes.

Inspired by these wine barrels, Kepler derived

formulas for the volumes of several solids of revolution

(not all of which were suitable for wine storage).

Among other results, he rediscovered Pappus’s for-

mula, 2πb πa

, for the volume of the torus, an inner-

tube-shaped solid that is generated when a disk of

radius a is revolved about an axis a distance b . a from

its center (Figure 1). The rigorous deductions of

Archimedes were somewhat beyond Kepler, who

resorted to the very free use of inﬁnitesimal arguments.

In Kepler’s own words: “we could obtain absolute and

perfect proofs from the books of Archimedes if we did

not shrink from the thorny reading of his writings.”

Kepler published the results of his investigations in

1615 at his own expense. Despite Kepler’s strenuous

efforts to recoup his outlay, sales were limited to one

nobleman, two mathematicians, and a library.

Arc Length

The arc length problem (known then as rectiﬁcation)

was also revived by mathematicians in the 1600s. Some

leading philosophers believed rectiﬁcation to be inso-

luble. Descartes, for one, was emphatic on this point in

his G

eom

etrie: “The ratios between straight and curved

lines are not known, and I believe cannot be discovered

by human minds.” The idea that it might be possible to

compare the arc lengths of two different curves seems

to have originated with another philosopher, Thomas

Hobbes (15881679). Hobbes communicated his idea

to Rober val in 1642, and, by the end of that year,

Roberval was able to prod uce equal length arcs of the

Archimedean spiral

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 y

5 arctanðy=xÞ (Figure 2a)

and of the parabola y 5 x

/2. Three years later,

m Figure 1

625

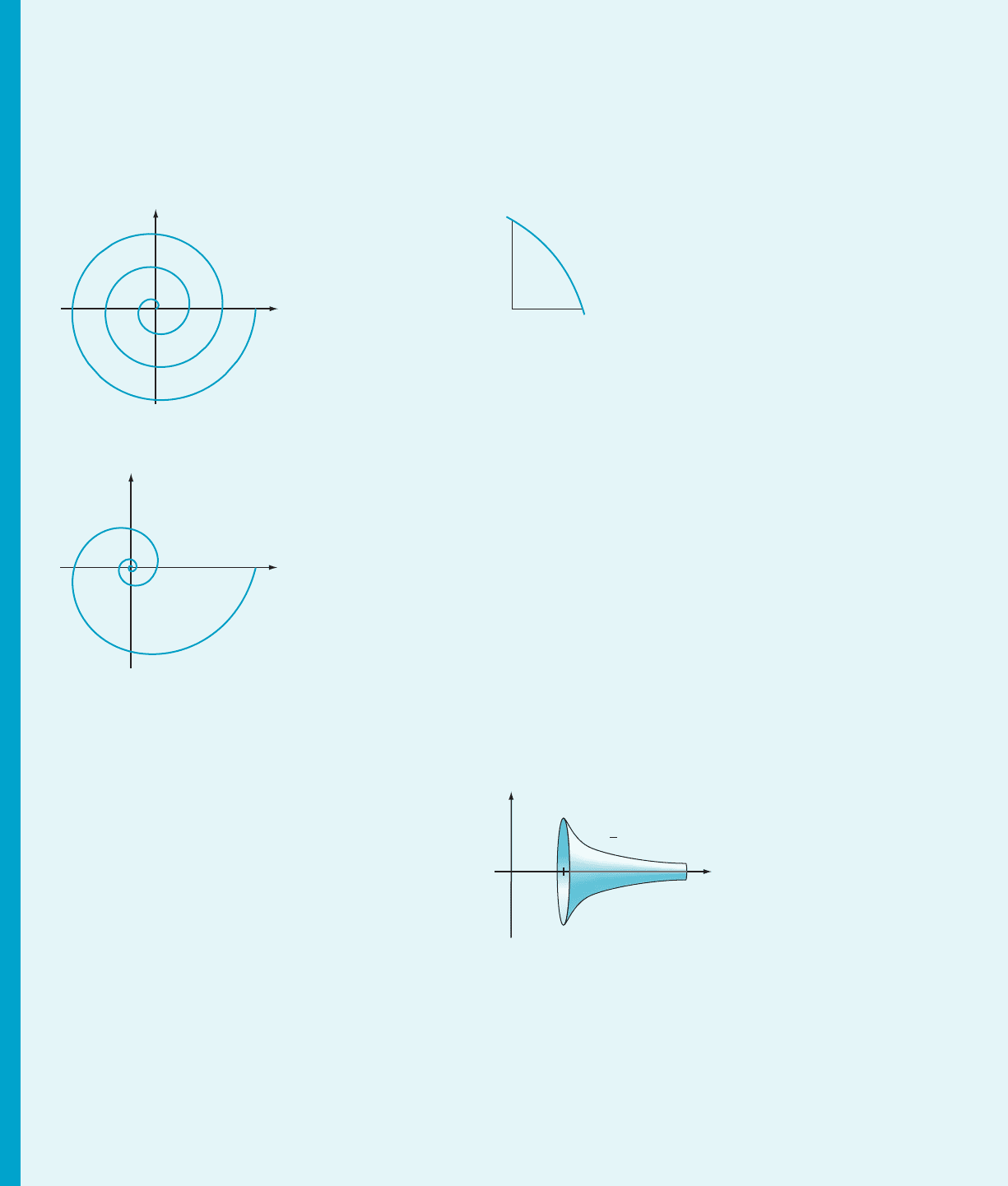
Evangelista Torricelli calculated the arc length of the

logarithmic spiral shown in Figure 2b.

After a twelve-year hiatus, a number of arc length

calculations were published in quick succession. In

1657, William Neile (16371670) rectiﬁed the semi-

cubical parabola y

5 ax

. One year later, Christopher

Wren (16321723), better known as the architect of St.

Paul’s Cathedral, computed the arc length of the

cycloid. In 1659, the general arc length integral,

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 ðdy=dx Þ

dx, was obtained more or less simul-

taneously by Hendrik van Heuraet (1633?) and Blaise

Pascal.

The characteristic triangle or differential triangle,

the right “triangle” with dx and dy for legs and ds for

“hypotenuse” (Figure 3), appeared in the writings of

Blaise Pascal, who became interested in rectiﬁcation

after learning of Wren’s result. During his study of

Pascal’s work in 1672, Leibniz realized that the differ-

ential triangle could become the basis of a method of

quadrature that supplemented its role in rectiﬁcation. It

was this insight about arc length that led Leibniz to the

formula for integration by parts and provided him with

his ﬁrst recognition of the relationship between tan-

gents (derivatives) and areas (integrals).

Torricelli’s Inﬁnitely Long Solid of Revolution

In 1641, Evangelista Torricelli studied the inﬁnitely

long solid that is obtained by rotating about the x-axis

the region in the ﬁrst quadrant that is bounded above

by the graph of y 5 1/x, below by the x-axis, and on the

left by x 5 1 (see Figure 4). What is particularly inter-

esting about this solid is that despite its inﬁnite length

and inﬁnite surface area, it has ﬁnite volume. As had

been the case in ancient Greece, philosophy was not yet

prepared for the mathematical consequences of the

inﬁnite. A spirited and personal exchange between

the philosopher Thomas Hobbes and the mathemati-

cian John Wallis erupted. As Wallis bluntly framed the

issue, an understanding of Torricelli’s solid “requires

more Geometry and Logic than Mr. Hobs is Master of.”

The reply of Hobbes was equally pointed: “I think Dr.

Wallis does wrong . . . for, to understand this for sense, it

is not required that a man should be a geometrician or a

logician but that he should be mad.”

The Catenary

The shape of a cable hanging freely under gravity

(Figure 5) was ﬁrst determined in 1690 by Leibniz, who

coined the name “catenary,” and, independently, by

x  a u cos(u)

y  a u sin(u)

m Figure 2a Archimedean spiral

x  a e

(bu)

cos(u)

y  a e

(bu)

sin(u)

m Figure 2b Logarithmic spiral

m Figure 3 Leibniz’s characteristic triangle

y 

m Figure 4 A section of Torricelli’s inﬁnitely long solid

626 Chapter 7 Applications of the Integral

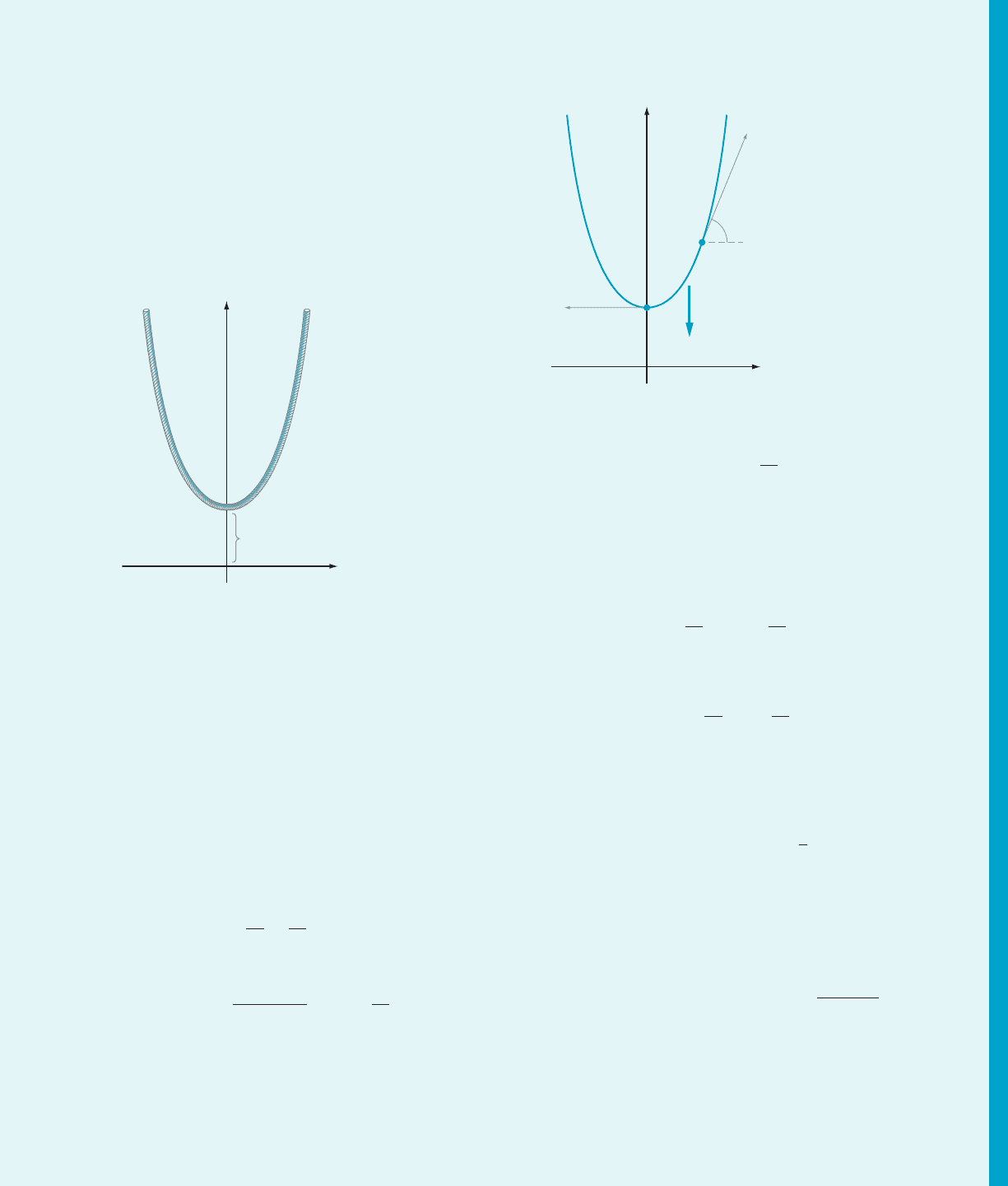
Jakob Bernoulli. One interesting method of determi n-

ing the mathematical formula of the catenary relies on

a “variational principle” similar to Fermat’s Principle

of Least Time (Genesis and Development 4). Among all

curves of ﬁxed length l joining two points P and Q, the

catenary arc of length l with endpoints P and Q has

lowest center of gravity, or, equivalently, the least

potential energy.

The theory of differential equations developed in

this chapter provides an alternative method for deriv-

ing the equation of the catenary. Let y(x) be the

function whose graph represents the hanging cable. Set

q(x)5y

(x). Two physical quantities are relevant: the

weight w of the cable per unit of length and the hor-

izontal tension T

at the lowest point of the cable (see

Figure 6). Because there is no lateral movement of the

cable, the horizontal forces must balance. When

translated into mathematics, the equation of horizontal

forces can be expressed by the separable ﬁrst order

differential equation.

ð1 1 q

1=2

We rewrite this equation as

ð1 1 q

1=2

dq 5

dx:

Using integration formula (3.10.16) with a 5 1, we

obtain

sinh

ðqÞ5

x 1 C:

We know that the cable has a horizontal tangent

when x 5 0, the abscissa of point A in Figure 6. Thus we

have q(0) 5 y

(0) 5 0. From this initial condition, we

see that C 5 0. Thus our solution becomes sinh

(q) 5

wx/T

or q(x) 5 sinh(wx/T

). But q 5 y

. Therefore

5 sinh





We integrate this last equation to obtain

yðxÞ5

cosh





1 h;

where h is a constant of integration. (If h

is the

height of the point A from the x-axis, then h 5 h

w.) In general, a curve whose equation is of the form

y 5 h 1 a  cosh





for positive constants a and h is called a catenary. The

Gateway Arch in St. Louis, Missouri is very nearly an

inverted catenary. Its architectural plans speci fy the

equation

y 5 693:8597 2 68:7672  cosh



3:0022

299:2239



for the centroids of its cross-sections (when x and y are

measured in feet).

Force of

gravity 5 ws

m Figure 6

m Figure 5

Genesis & Development 627

The Catenoid

Suppose that P5(a, α) and Q5(b, β) are points in the

plane that lie above the x -axis. Suppose that P and Q

are joined by a curve C that is an arc of the graph of

a function f. Rotating C about the x-axis generates a

surface of revolution. Euler posed the question,

“Among all such surfaces of revolution, which has

minimal surface area?” Analytically, the question may

be asked in this way: Which function f satisﬁes f(a) 5 α

and f(b) 5 β and minimizes the integral

Iðf Þ5 2π

f ðxÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1



ðxÞ



dx ?

The task of ﬁnding a function that minimizes an

integral such as I( f ) is substantially more complicated

than ﬁnding an extremum of a numerical function. This

kind of problem is studied in a branch of mathematics

called the calculus of variations. Euler solved his own

problem, pro ving that I( f ) is minimized when C is the

arc of a catenary. The surface of revolution is called a

catenoid. It arises naturally—indeed, you can generate

a catenoid with some wire and soapy water. Form wires

in the shape of two circles with different radii, bring

them together in a soap solution, and draw them apart

so that they are circles of revolution about the same

axis. The resulting soap ﬁlm stretching between the two

circular wires will assume the shape of a catenoid. In

general, soap ﬁlms give minimal surfaces. This fact can

be proved from thei r surface tension equati ons.

628 Chapter 7 Applications of the Integral

CHAPTER 8

Inﬁnite Series

When we learn to write fractions in decimal form, we soon become aware that

some numbers result in a nonterminating sequence of digits. For example, when we

decimalize 1/3, we apply the long division algorithm. No matter how many times

we divide, we are left with a remainder. If we terminate the procedure after any

division, then we are left with 0.33 . . . 33, which is a little too small. If we round up

to 0.33 . . . 34, then the result is a number that is a little too great. We must

therefore accept that the decimalization of 1/3 is 0.333 . . . without end.

Of course, in grade school we do not pause long to reﬂect on the inﬁnite

process that is symbolized by the trailing dots. Intuitively, we understand that the

notation must stand for the “inﬁnite sum”

100

1000

10000

1 

;

even if we have only a fuzzy idea of what that might mean.

Now that we have studied some calculus we are prepared to understand exactly

what such sums signify. The concept of “limit” that is needed for the inﬁnite

processes of calculus is just what is needed to understand the inﬁnite sums that arise

in grade school and elsewhere. In fact, our approach is nothing more than a

framework for turning our intuition into something precise. If you think of the

sequence

0:3 5

; 0:33 5

100

; 0:333 5

100

1000

; :::

as a sequence of approximations of 1/3 that become ever more accurate, then you

already have the key idea of understanding an “inﬁnite sum” as a limit of its

“partial sums.”

Inﬁnite sums are important in calculus, but they are not conﬁned to mathe-

matical disciplines. If you study scientiﬁc subjects such as biology or thermo-

dynamics, then you are likely to encounter inﬁnite sums in those pursuits. If you

learn about the money supply in economics or annuities in ﬁnance, then you will

see that inﬁnite sums are needed for those concepts. This chapter will provide you

with a good basis for your understanding of inﬁnite sums, wherever they arise.

In this chapter, we also study inﬁnite sums

n50

ðx 2 cÞ

for which x is

treated as a variable lying in an interval centered at c. Such power series, as they are

PREVIEW

629

called, have found many applications in mathematics and science. Several impor-

tant differential equations from physics and engineering are best solved by power

series methods. Functions deﬁned by power series have become fundamental tools

in the study of diverse subjects such as civil engineering, aeronautics, structural

geology, and celestial mechanics.

Power series are not used only to create new functions. In many cases, it is

important to be able to express the standard elementary functions by means of

power series. The question becomes, given a function f and a point c, can we ﬁnd

coefﬁcients {a

} for which f ðxÞ5

n50

ðx 2 cÞ

? The answer lies in the theory of

Taylor series, which is the focus of the last two sections of this chapter. Because

the partial sums

n50

ðx 2 cÞ

of a power serie s are polynomials, our study of

Taylor series will lead to powerful techniques for approximating functions by

polynomials.

630

8.1 Series

The idea of adding together ﬁnitely many numbers is a simple and familiar one. We

are so used to the properties of ﬁnite sums that we tend not to think about them.

Now we will learn about sums of inﬁnitely many numbers, and we will have to be a

bit more careful. As the next example shows, contradictions can arise if we do not

establish certain ground rules.

⁄ EX

AMPLE 1 Group the terms of 21 1 1 2 1 1 1 2 1 1 1 2 1 1  in two

ways to produce diff erent results.

Solution If

we group the terms as (21 1 1) 1 (21 1 1) 1 (21 1 1) 1 

then the

sum seems to be 0 1 0 1 0 1 

which ought to be 0. On the other hand, if we

group the terms as 21 1 (1 2 1) 1 (1 2 1) 1 (1 2 1) 1 

then the sum seems to

be 21 1 0 1 0 1 0 1 

which ought to be 21. Apparently the associative law of

addition fails for this inﬁnite sum.

Example 1 points to the need for a precise deﬁnition that establishes what it

means to add inﬁnitely many numbers. With a carefu lly conceived deﬁnition, sums

such as 21 1 1 2 1 1 1 2 1 1 1 2 1 1 are not given any meaning, and ambiguities

such as that of Example 1 do not arise. The key idea in the precise deﬁnition of an

inﬁnite sum is the notion of a limit of a sequence. It is that concept that we review

next.

Limits of Inﬁnite

Sequences—A Review

Recall that an inﬁnite sequence fa

n51

is a list a

, a

, . . . of terms indexed by the

positive integers. For example, 1, 1/2, 1/4, 1/8, 1/16, . . . is the inﬁnite sequence

f1=2

n21

n51

of nonnegative powers of 1/2. Often it is convenient to begin a

sequence with a ﬁrst index that differs from 1. Thus f1=2

n50

is another way to

write the sequence 1, 1/2, 1/4, 1/8, 1/16, . . . .

We say that a sequence fa

n51

converges to a real number ‘ (or has limit ‘) if,

for each A . 0, there is an integer N such that ja

2 ‘j, A for all n $ N. In this case,

we write lim

n-N

5 ‘, or, equivalently, a

- ‘ as n -N. A sequence that has a

limit is said to be convergent. If a sequence does not converge, then we say that it

diverges, and we call it a divergent sequence. Some ba sic convergent sequences are

lim

n-N

5 0ifr is a consta nt with jrj, 1; ð8:1:1Þ

lim

n-N

1=n

5 1ifb is a positive constant ; ð8:1:2Þ

and

lim

n-N

5 0ifp is a positive constant: ð8:1:3Þ

There are a few rules that, when used with these basic limits, enable us to easily

evaluate the limits of many common sequences. For example, if fa

n51

and

n51

are convergent sequen ces, and if α is any real number, then

lim

n-N

5 β; if c

5 β for all n; ð8:1:4Þ

lim

n-N

ðα  a

Þ5 α  lim

n-N

; ð8:1:5Þ

8.1 Series 631

lim

n-N

ða

1 b

Þ5 lim

n-N

1 lim

n-N

; ð8:1:6Þ

lim

n-N

ða

2 b

Þ5 lim

n-N

2 lim

n-N

; ð8:1:7Þ

lim

n-N

ða

 b

Þ5 ð lim

n-N

Þðlim

n-N

Þ; ð8:1:8Þ

and

lim

n-N

lim

n-N

lim

n-N

if lim

n-N

6¼ 0: ð8:1:9Þ

⁄ EX

AMPLE 2 Let

1 3

ﬃﬃﬃ

2 5

1 10

Use limit formula (8.1.3) to calculate lim

n-N

Solution We

divide each summand in the numerator and denominator of a

by the

highest power, n

, obtaining

lim

n-N

5 lim

n-N

2 1 3

ﬃﬃﬃ

2 5=n

3 1 10=n

Observing that

lim

n-N



2 1 3

ﬃﬃﬃ



5 lim

n-N

ð2Þ1 lim

n-N

7=2

2 lim

n-N





5 2 1 3  lim

n-N

7=2

2 5  lim

n-N





5 2 1 3  0 2 5  0 5 2

and

lim

n-N



3 1



5 lim

n-N

ð3Þ1 lim

n-N

5 3 1 10  lim

n-N

5 3 1 10  0 5 3 6¼ 0;

we use limit formula (8.1.9) to conclude that lim

n-N

5 2=3. ¥

Example 2 has a generalization that is used frequently. If p

, p

, ...,p

and q

,...,q

‘

are constants with p

. p

. ... . p

$ 0 and q

. q

. ... . q

‘

$ 0, and

if c

, c

,...,c

and d

, d

, ..., d

‘

are constants with c

6¼0 and d

6¼0, then

lim

n-N

1 c

1 1 c

1 d

1 1 d

‘

if p

5 q

0ifp

, q

ð8:1:10Þ

In words, if the highest power in the numerator is the same as the highest power in

the denominator, then the limit is the ratio of the coefﬁcients of the highest powers.

If the highest power in the numerator is less than the highest power in the

denominator, then the limit is 0.

In another important technique for calculating lim

n-N

, we treat the index

variable n as a continuous variable x that tends to inﬁnity. Then we may apply

tools from calculus, such as l’Ho

pital’s Rule. The next two examples illustrate

this idea.

632 Chapter 8 Inﬁnite Series

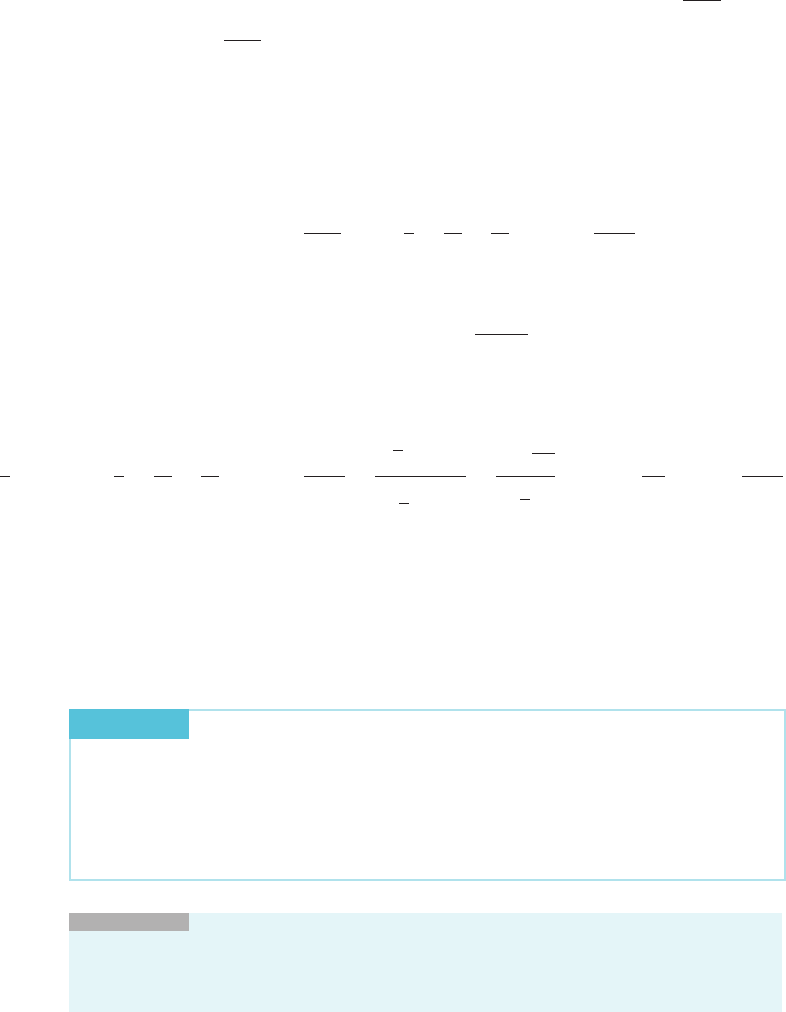
⁄ EXAMPLE 3 Let a

5 n/e

λn

where λ is a positive constant. Calculate

lim

n-N

Solution Becau

se λ . 0, we have lim

n-N

λn

5 N and lim

n-N

has the

indeterminate form

. An application of l’Ho

pital’s Rule shows that

lim

x-N

λx

5 lim

x-N

λx

5 lim

x-N

λe

5 0:

If we restrict the approach of x to inﬁnity through integer values n, then we obtain

lim

n-N

5 0. ¥

⁄ EXAMPLE 4 Show that

lim

n-N

1=n

5 1: ð8:1:11Þ

Solution In

Example 10 of Section 4.7, we used l’Ho

pital’s Rule to show that

lim

x-N

1=x

5 1. If we restrict the approach of x to inﬁnity through integer values n,

then we obtain limit formula (8.1.11).

The Deﬁnition of an

Inﬁnite Series

If a

, a

, . . . is an inﬁnite sequence, then the (formal) expression a

1 a

1 

is said to be an inﬁnite series. It is convenient to extend the sigma notation

n5M

5 a

1 a

M11

1 1 a

N21

1 a

for ﬁnite sums that we introduced in Section 5.1 of Chapter 5. To signify an inﬁnite

series, we simply use the symbol N for the upper limit of summation. Thus we let

n51

denote the inﬁnite series a

1 a

1  For instance, if a

5 1/2

n21

then

n51

denotes the inﬁnite series 1 1 1/2 1 1/4 1 1/8 1 1/16 1 

Example 1 suggests that care is needed if we are to assign a value to the inﬁnite

series

n51

. Nevertheless, there is a quite natural way to deﬁne and interpret

inﬁnite series. Consider the decimalization of 1/3, namely 0.3333 . . . (ad inﬁnitum).

In realit y, the decimal number 0.3333 . . . symbolizes the inﬁnite series

n51

with

5 3/10

. If we need a decimal expansion that is accurate to two decimal places,

then we use a

1 a

5 0.33. If we require ﬁve decimal digits of 1/3, then we use

1 a

5 0.33333, and so on. By taking “partial sums” of the inﬁnite

series

n51

, we obtain approximations that become closer and closer to the exact

value of

n51

. This familiar example suggests the method by which we deﬁne the

“sum” of an inﬁnite series in general.

DEFINITION

If a

, a

, . . . is an inﬁnite sequence, then we say that the

expression

n51

5 a

1 a

1 1 a

is a partial sum of the inﬁnite series

n51

. The sequence fS

N51

is said to be

the sequence of partial sums of the inﬁnite series

n51

8.1 Series 633

⁄ EXAMPLE 5 Compute the sequence of partial sums of the inﬁnite series

n51

ð21Þ

Solution Accord

ing to the deﬁnition, S

n51

ð21Þ

521, S

n51

ð21Þ

1 ð21Þ

521 1 1 5 0, S

n51

ð21Þ

5 ð21Þ

1 ð21Þ

521, and

so on. The sequence of partial sums of

n51

ð21Þ

is 21; 0; 21; 0; 21; 0;::: ¥

⁄ EXAMPLE 6 Find a formula for the partial sum S

n51

n21

of the

inﬁnite series

n51

n21

Solution For

small values of N, ordinary addition yields the values of S

. For

example, we have S

5 1/2

5 1, S

5 1/2

1 1/2

5 3/2, S

5 1/2

1 1/2

5 7/4,

and so on. More efﬁciently, whenev er we calc ulate one partial sum, we can obtain

the next partial sum by adding the next term of the series. Thus S

5 S

1 1/2

7/4 1 1/8 5 15/8. To calculate the partial sum

n51

n21

5 1 1

1 1

N21

that corresponds to a general value of N, we use equation

1 1 r 1 r

1 1 r

N21

2 1

r 2 1

; r 6¼ 1 ð8:1:12Þ

from Theorem 4 of Section 2.5 in Chapter 2. If we specify r 5 1/2 in equation

(8.1.12), we see that

n51





n21

5 1 1

1 1

N21





2 1





2 1

1 2

5 2



1 2



5 2 2

N21

This general formula agrees with the speciﬁc calculations of S

for small values of

N that we performed at the beginning of the solution.

Convergence of

Inﬁnite Series

The meanin g that we give to the “sum” of an inﬁni te series

n51

is determined

by the behavior of its sequence {S

} of partial sums as N tends to inﬁnity.

DEFINITION

Let {S

} be the sequence of partial sums of an inﬁnite series

n51

. If lim

N-N

5 S, then we say that the inﬁnite series

n51

converges

to S. In this case, when we refer to

n51

, we mean the number S, and we

write

n51

5 S. We call S the sum or value of the inﬁnite series. If the

sequence {S

} does not converge, then we say that the series diverges. A series

that converges is said to be convergent; otherwise, we say that it is divergent.

INSIGHT

The terms “convergent” and “divergent” suggest an analogy between

inﬁnite series

n51

and improper integrals

f ðxÞdx. Indeed, the approaches to the

two concepts are similar. To calculate

f ðxÞdx, we compute

f ðxÞdx for large values

of N and take the limit of

f ðxÞdx as N tends to inﬁnity. Analogously, to calculate

634 Chapter 8 Inﬁnite Series