Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


where C is the constant of integration. We can determine the two constants C and k
from the two given observations: y(0) 5 1/60 and y(6000) 5 1/140. The first data
point yields
2
1
1=60
52k 0 1 C
or C 5260. The second data point yields
2
1
1=140
52k 6000 2 60
or k 5 1/75. Thus 21/y(t) 52t/75 2 60. Solving for y(t), we obtain y(t) 5 75/
(t 1 4500). Therefore y(10500) 5 75/(10500 1 4500) 5 1/200 moles/L.
¥
⁄ EXAMPLE 8 Let y(t) and v(t) 5 dy/dt be the height and velocity of a
projectile that has been shot straight up from the surface of Earth with initial
velocity v
0
. Newton’s Law of Gravitation states that
dv
dt
52
gR
2
ðR 1 yÞ
2
;
where R is the radius of Earth, and g is the acceleration due to gravity at Earth’s
surface. Supposing that v
0
,
ffiffiffiffiffiffiffiffiffi
2gR
p
, what is the maximum height attained by the
projectile?
Solution At
the instant the projectile reaches its maximum height and begins to
fall back to Earth, its velocity v is 0. Therefore our strategy is to find v as a function
of y and solve for the value of y for which v 5 0. As a first step, we use the Chain
Rule to express dv/dt in terms of dv/dy:
dv
dt
5
dv
dy
dy
dt
5
dv
dy
v:
By equating this expression for dv/dt with the one given by Newton’s Law of
Gravitation, we obtain
v
dv
dy
52
gR
2
ðR 1 yÞ
2
:
This differential equation is separable. Following the general procedure, we obtain
Z
vdv5
Z
2
gR
2
ðR 1 yÞ
2
dy
or
1
2
v
2
5 gR
2
ðR 1 yÞ
21
1 C:
When y 5 0, we have v 5 v
0
. Therefore
1
2
v
2
0
5 gR
2
ðR 1 0Þ
21
1 C;
or C 5
1
2
v
2
0
2 gR. It follows that
1
2
v
2
5 gR
2
ðR 1 yÞ
21
1
1
2
v
2
0
2 gR
: ð7:6:7Þ
7.6 First Order Differential Equations—Separable Equations 595

Now we set v 5 0 in equation (7.6.7) and solve for y . We find that the maximum
height is v
2
0
R=ð2gR 2 v
2
0
Þ. ¥
Logistic Growth Figure 6 shows the growth of a pumpkin in a controlled agricultural experiment. At
first the growth of the pumpkin appears to be exponential. But the growth plot
eventually becomes concave down and can no longer be modeled by exponential
growth. To obtain a more accurate model, scientists often make the following
growth assumptions:
a. There is a size P
N
that cannot be exceeded. In population models, the constant
P
N
is called the carrying capacity;
b. P
0
ðtÞ-0asPðtÞ-P
N
. In words, as the function P(t) approaches the carrying
capacity P
N
, its rate of growth decreases to 0.
One way to incorporate these assumptions into a growth model is to assume that
the
rate of population increase is jointly proportional to the population P(t) and to
P
N
2P(t). The resulting differential equation
dP
dt
5 k PðtÞ
P
N
2 PðtÞ
; Pð0Þ5 P
0
ð7:6:8Þ
is called the logistic growth equation. In this differential equation k, P
0
, and P
N
represent fixed positive constants. In our discussion, we will assume that P
0
, P
N
.
Using the method of separation of variables, we can rewrite equation (7.6.8) as
Z
1
P ðP
N
2 PÞ
dP
dt
dt 5
Z
kdt;
or
Z
1
P ðP
N
2 PÞ
dP 5
Z
kdt: ð7:6:9Þ
⁄ EX
AMPLE 9 Use the method of partial fractions to solve equation (7.6.9).
Solution We
apply partial fractio ns and write
1
P ðP
N
2 PÞ
5
A
P
1
B
P
N
2 P
:
Before we go any further, it is a good idea to make sure that we understand the role
of each quantity in this equation. Here P
N
is a fixed constant that we regard as
known, even though we are not given a specific numerical value. The quantity P is a
variable. We are to find values for the unknown constants A and B so that the
equation is valid for all values of P. Putting the right side over a common
denominator and equating numerators leads to the equation
1 5 A ðP
N
2 PÞ1 B P:
If we let P be 0, then we find that A 5 1/P
N
. Letting P be P
N
results in B 5 1/P
N
.
With these values, equation (7.6.9) becomes
Z
1
P
N
1
P
1
1
P
N
2 P
dt 5
Z
kdt;
4 8 12 16
50
40
30
20
10
Diameter (cm)
Time
(
weeks
)
m Figure 6 Pumpkin growth
596 Chapter 7 Applications of the Integral

or
1
P
N
Z
1
P
dt 1
1
P
N
Z
1
P
N
2 P
dt 5 kt 1 C;
or
1
P
N
lnðPÞ2 lnð P
N
2 PÞ
5 kt 1 C:
We have omitted absolute values in the logarithms because P(t) is in the range
0 , P(t) , P
N
. We can combine the logarithms to obtain
ln
PðtÞ
P
N
2 PðtÞ
5 P
N
ðkt 1 CÞ
or, on exponentiating and letting A 5 expðP
N
CÞ ,
PðtÞ
P
N
2 PðtÞ
5 expðP
N
kt 1 P
N
CÞ5 expðP
N
ktÞexpðP
N
CÞ5 A expðP
N
ktÞ:
We may solve for the constant A by substituting t 5 0:
P
0
P
N
2 P
0
5
Pð0Þ
P
N
2 Pð0Þ
5 A:
Therefore
PðtÞ
P
N
2 PðtÞ
5
P
0
P
N
2 P
0
expðP
N
ktÞ:
Isolating P(t) is elem entary but somewhat tedious. The result is
PðtÞ5
P
0
P
N
P
0
1 ðP
N
2 P
0
Þexpð2k P
N
tÞ
: ð7:6:10Þ ¥
The function P defin
ed by equation (7.6.10) is said to be a logistic growth
function. The term sigmoidal growth is also used in biology. Notice that there are
three positive constants that determine logistic growth: the proportionality constant
k, the initial value P
0
of P, and the carrying capacity P
N
. The graph of P (t)
a. is everywhere rising,
b. is concave up for P
0
# P ,
1
2
P
N
c. is concave down for
1
2
P
N
, P , P
N
, and
d. has y 5 P
N
as a horizontal asymptote.
We can deduce property a by noticing that, because P
N
2 P
0
, k,andP
N
are all
positive, the expression (P
N
2 P
0
) exp (2 k P
N
t) is decreasing. Because this
expression appears in the denominator of formula (7.6.10) for P(t), we conclude
that P(t) is increasing. Property d can be expressed as
lim
t-N
PðtÞ5 P
N
;
which is the reason for the subscript N. This limiting value for P(t) is an immediate
consequence of formula (7.6.10):
lim
t-N
PðtÞ5 lim
t-N
P
0
P
N
P
0
1 ðP
N
2 P
0
Þexpð2k P
N
tÞ
5 lim
t-N
P
0
P
N
P
0
1 ðP
N
2 P
0
Þ0
5 P
N
:
7.6 First Order Differential Equations—Separable Equations 597
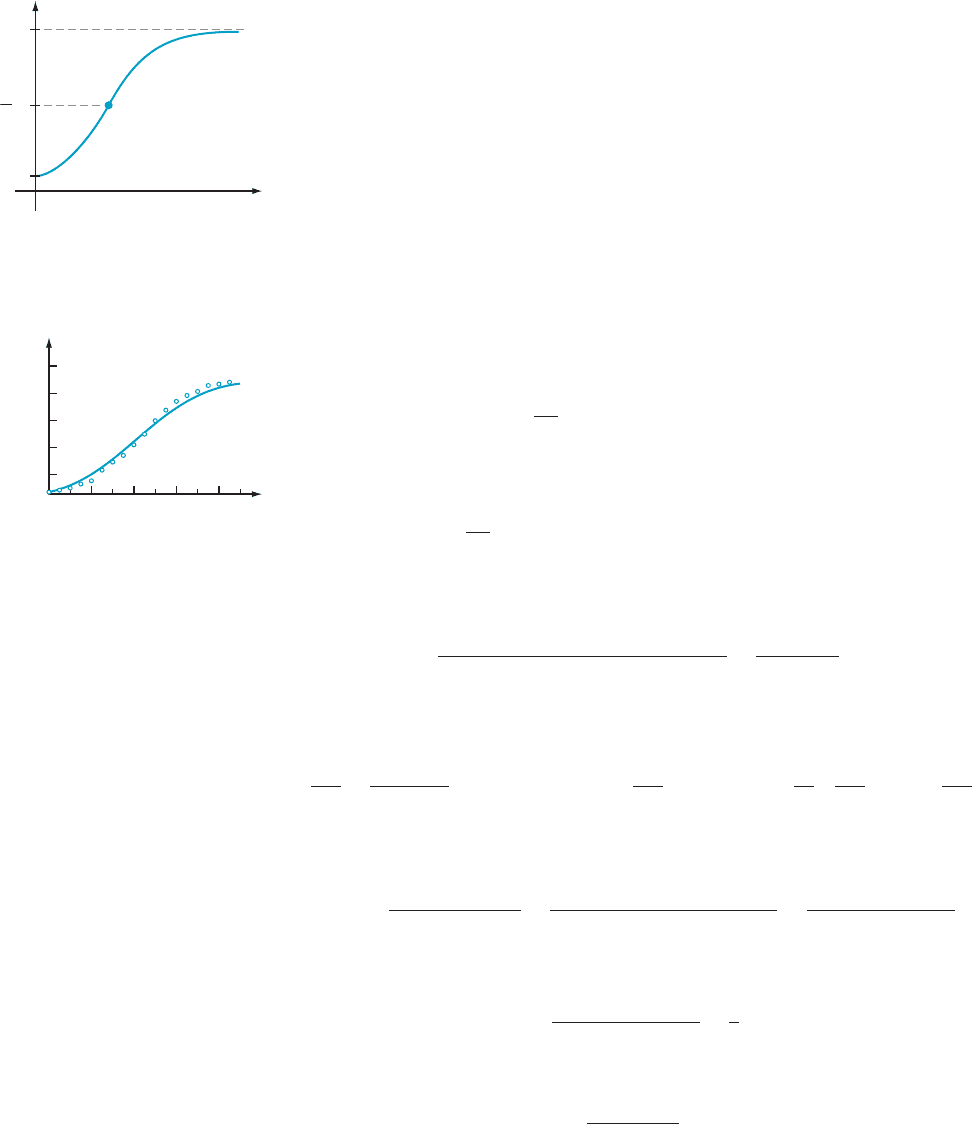
A proof of properties b and c is outlined in Exercise 55. A typical logistic curve is
plotted in Figure 7. In Figure 8, we have replotted the pumpkin-growth data, ad ding
the graph of the logistic function determined by P
0
5 3.6, P
N
5 46, and k 5 0.0065.
⁄ EX
AMPLE 10 Suppose that 100 children attend a day-care center. Let
P(t) be the fracti on of the day-care population with a viral infection at time t
(measured in days). Suppose that, at 9 AM on Monday (t 5 0), only 1 child was
infected. Suppose that, at 9 AM on Tuesday (t 5 1), there were 3 infected children
(including the origin al child). Assume that the rate of change of P is jointly pro-
portional to P (because P represents the fraction of the population capable of
spreading the infection) and 1 2 P (because 1 2 P represents the fraction of the
population that can still be infected). By when did the infe ction spread to half the
day-care population?
Solution Because
the rate of change of P is jointly proportional to P and 1 2 P,we
have
dP
dt
5 k PðtÞ
1 2 PðtÞ
;
for some proportionality constant k. Because 1 child out of 100 was infected at time
t 5 0, we have P(0) 5 1/100. Thus the initial value problem for P(t)is
dP
dt
5 k PðtÞ
1 2 PðtÞ
; Pð0Þ5 1=100:
Notice that this initial value problem is logistic growth equation (7.6.8) with P
N
5 1
and P
0
5 1/100. The solution is given by formula (7.6.10):
PðtÞ5
1=100
1=100 1 ð1 2 1=100Þexpð2k 1 tÞ
5
1
1 1 99e
2kt
: ð7:6:11Þ
We may now use the observation P(1) 5 3/100 to solve for k. Because formula
(7.6.11) gives us P(1) 5 1/(1 1 99e
2k
), we obtain
3
100
5
1
1 1 99e
2k
; or 1 1 99e
2k
5
100
3
; or e
2k
5
1
99
100
3
2 1
5
97
297
:
By applying the natural logarithm to each side of the last equation, we see that
2k 5 ln(97/297). Our final expression for P is
PðtÞ5
1
1 1 99e
tlnð97=297Þ
5
1
1 1 99 exp
ln
ð97=297Þ
t
5
1
1 1 99 ð97=297Þ
t
:
The solution to our problem is found by solving the equation
1
1 1 99 ð97=297Þ
t
5
1
2
for t. After some simplification, we obtain 99 5 (297/97)
t
or
t 5
lnð99Þ
lnð297=97Þ
4:1:
According to our model, about 4.1 days after the first child was infected, that is to
say, by about 11:30 Friday morning, the fiftieth child became infected.
¥
4 8 12 16
50
40
30
20
10
Diameter (cm)
Time
(
weeks
)
m Figure 8 Pumpkin growth
t
y
P
P(t)
Horizontal asymptote
Point of inflection
P
1
2
P
0
m Figure 7 Logistic growth curve
598 Chapter 7 Applications of the Integral

QUICK QUIZ
1. To which of the following differential equations can we apply the method
of separation of variables: a) dy=dx 5 expðxyÞ,b)dy=dx 5 expðx 1 yÞ,
c) dy=dx 5 lnðx
y
Þ,ord)dy=dx 5 ln ðx 1 yÞ?
2. Solve 4 dy=dx 5 3x
2
=ðy
3
1 y 1 5Þ.
3. Solve the initial value problem dy=dx 5 x=y; yð2Þ5 3.
4. If dy=dx 5 sinðx
3
Þ and yðπÞ5 2, then for what α, β, and C is
yðxÞ5 C 1
R
β
α
sinðt
3
Þdt?
Answers
1. b and c 2. y
4
1 2y
2
1 20y 5 x
3
1 C 3. y
2
5 x
2
1 5
4. α 5 π, β 5 x,andC 5 2
EXERCISES
Problems for Practice
c In Exercises 128, verify that the given function y satisfies
the given differential equation. In each expression for y(x),
the letter C denotes a constant. b
1.
dy
dx
5 xy; yðxÞ5 Ce
x
2
=2
2.
dy
dx
5 2xy
2
; yðxÞ5 1=ðC 2 x
2
Þ
3.
dy
dx
5 x 2 3y; yð xÞ5 x=3 2 1=9 1 Ce
23x
4.
dy
dx
5 e
x
1 y; yðxÞ5 e
x
ðx 1 C Þ
5.
dy
dx
5 x 1 y; yð xÞ5 Ce
x
2 x 2 1
6.
dy
dx
5 x 1 xy; yðxÞ5 Ce
x
2
=2
2 1
7.
dy
dx
5 y 1 x
2
; yðxÞ5 Ce
x
2 x
2
2 2x 2 2
8.
dy
dx
5
2x 2 y
x 1 y
; y 52x 1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3x
2
1 2C
p
c In each of Exercises 9218, solve the given differential
equation. b
9.
dy
dx
5 6
ffiffiffiffiffi
xy
p
10. ð4 1 y
2
Þ
dy
dx
5 x
2
11. ð2 1 xÞ
dy
dx
5 y
2
12.
dy
dx
1 3xy
2
5 0
13.
dy
dx
2 3x
2
y 5 0
14. x
dy
dx
2 y 5 3x
3
y
15. expð2x 1 3yÞ
dy
dx
5 1
16. cotðxÞ
dy
dx
5 tanðyÞ
17.
dy
dx
5 x secðyÞ
18.
dy
dx
5 y secðxÞ
c In Exercises 19236, find the solution of the given initial
value
problem. b
19. y
0
ðxÞ5 2xyð1Þ5 3
20. y
0
ðxÞ5 2x 1 1 yð1Þ5 5
21. y
0
ðxÞ5 cosðxÞ yð0Þ5 2
22. y
0
ðxÞ5 sec
2
ðxÞ yðπ=4Þ5 3
23. y
0
ðxÞ5 x=yðxÞ yð0Þ5 1
24. y
0
ðxÞ5 xy
2
ðxÞ yð1Þ5 2
25. y
0
ðxÞ5 y
2
ðxÞsinðxÞ yð0Þ5 2
26. x
3
dy
dx
5 cos
2
ðyÞ yð0Þ5 1
27. y
dy
dx
5
2x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 y
2
p
yð0Þ5 0
28. y
0
ðxÞ5 cosðxÞ=yðxÞ yð0Þ5 2
29.
dy
dx
5 y 1
1
y
yð0Þ5 3
30. ð1 1 x
2
Þ
4
y
0
ðxÞ5 6xyðxÞ yð0Þ5 1
31. x
2
y
0
ðxÞ5 yðxÞsinð1=xÞ yð2=πÞ5 3
32.
dy
dx
5 expðx 1 yÞ yð0Þ5 0
33. y
0
ðxÞ2 xy
2
5 xyð4x 2 yÞ yð0Þ5 1
34.
dy
dx
5 x 2 1 1 yx 2 yyð2Þ5 3
35.
dy
dx
5
1
yð1 1 x
2
Þ
yð1Þ5
ffiffiffi
π
p
36.
dy
dx
5 2x cos
yðxÞ
yð0Þ5 0
Further Theory and Practice
37. Match the functions F
1
(x, y) 5 x, F
2
(x, y) 5 y, F
3
(x, y) 5
xy, F
4
(x, y) 5 x/y, F
5
(x, y) 5 x
2
2 y
2
, and F
6
(x, y) 5 y
2
to
the graphs of the slope fields of equation (7.6.1) that are
plotted in Figures 9a through 9f.
7.6 First Order Differential Equations—Separable Equations 599
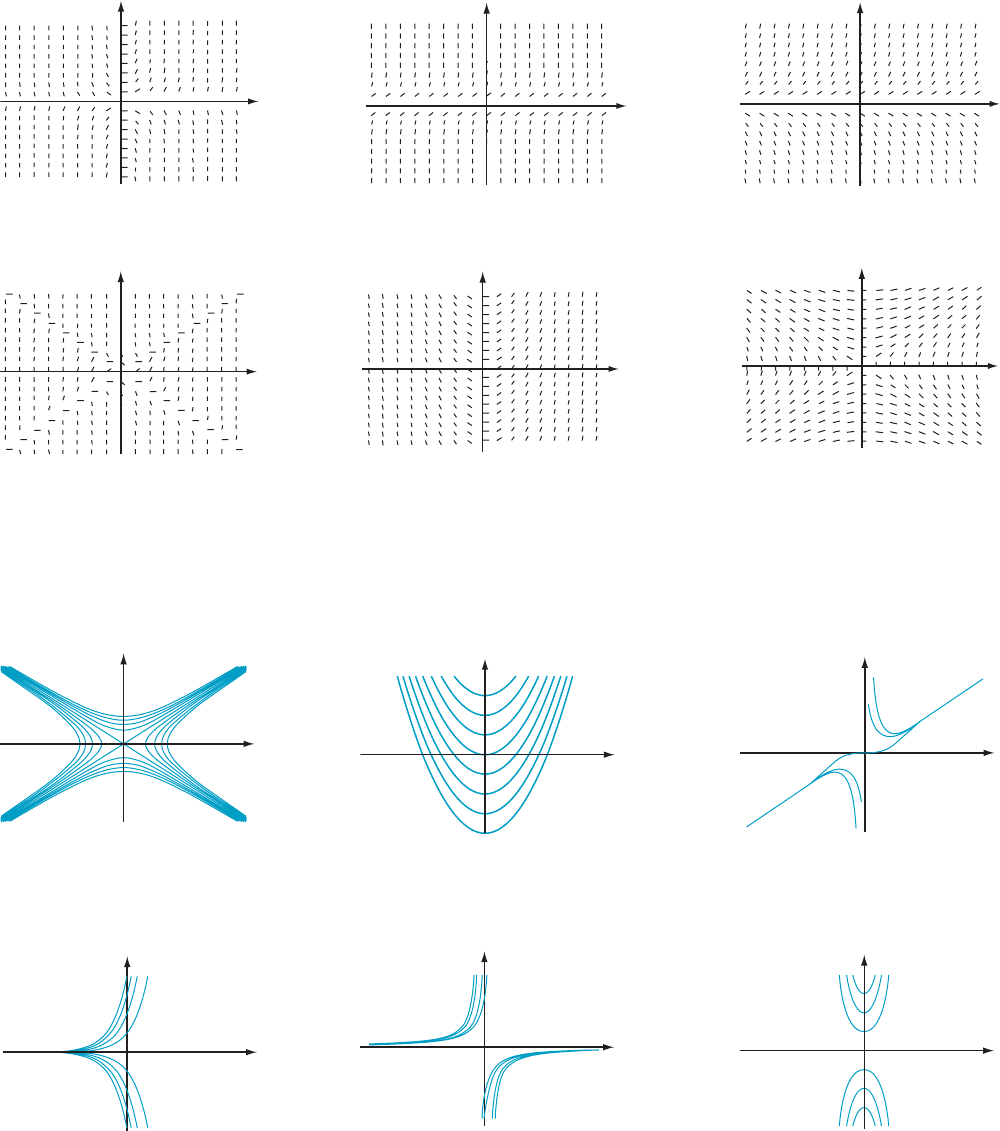
y
x
m Figure 9a
y
x
m Figure 9b
y
x
m Figure 9c
y
x
m Figure 9d
y
x
m Figure 9e
y
x
m Figure 9f
38. Match
the graphs of the solution curves in Figures 10a
through 10f to the slope fields of Figures 9a through 9f.
y
x
m Figure 10a
y
x
m Figure 10b
y
x
m Figure 10c
y
x
m Figure 10d
y
x
m Figure 10e
y
x
m Figure 10f
600 Chapter
7 Applications of the Integral
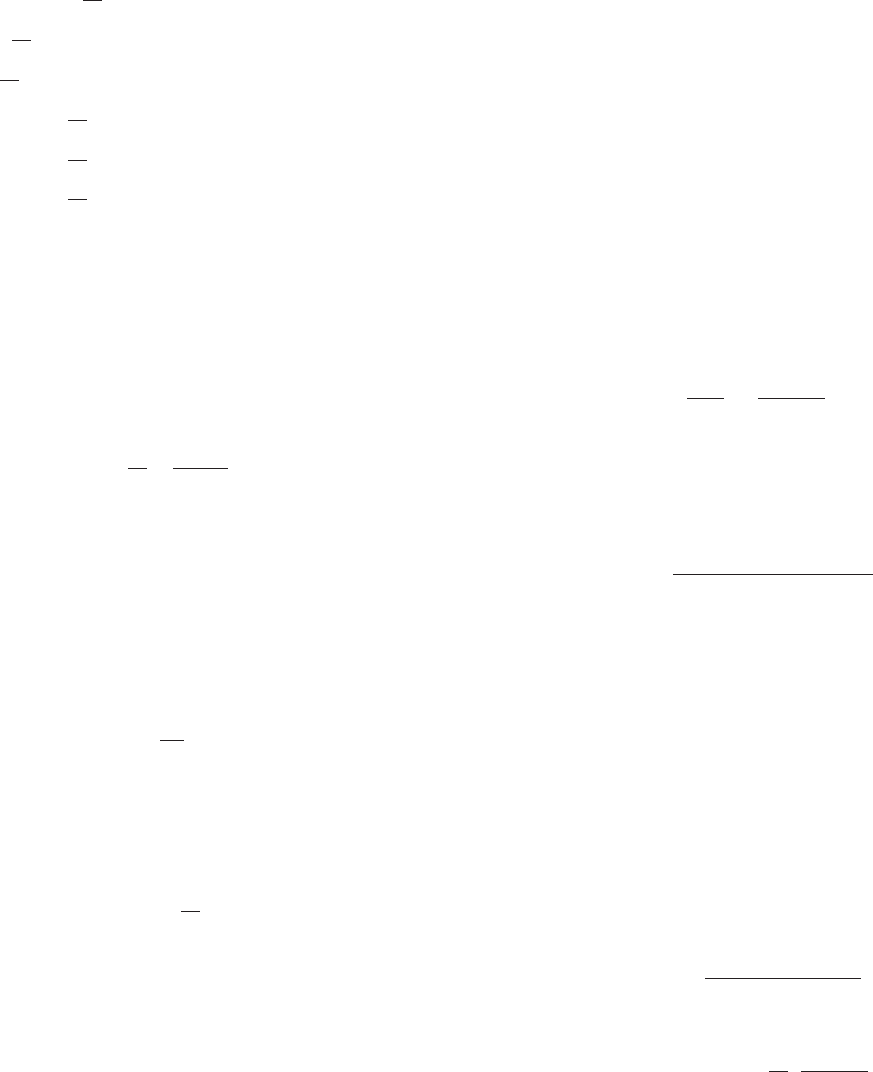
c In each of Exercises 39244, solve the given differential
equation. b
39. expðx 1 yÞ
dy
dx
5 x
40. y
dy
dx
5 x
3
cscðy Þ
41.
dy
dx
5 3x
2
ðy
2
2 yÞ
42. ð4 1 e
2x
Þ
dy
dx
5 y
43. ð4 1 e
2x
Þ
dy
dx
5 ye
x
44. ð4 1 e
2x
Þ
dy
dx
5 ye
2x
45. Solve the initial value problem y
0
ðxÞ5 4f
3
ðxÞf
0
ðxÞ;
f ð1Þ5 2; yð1Þ5 24. Verify your formula with f ðxÞ5 2
ffiffiffi
x
p
.
46. Solve the initial value problem y
0
ðxÞ5 xg
0
ðx
2
Þ; gð4Þ5 6;
yð2Þ5 12. Verify your formula with g(x) 5 x
2
2 2x 2 2.
47. Solve the initial value problem y
0
ðxÞ5 f
0
ðxÞg
0
f ðxÞ
;
f ð0Þ5 3; gð3Þ5 2; y ð0Þ5 6. Verify your formula with
f ðxÞ5 3 cosðxÞand gðxÞ5
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
.
48. Show that, when applied to the initial value problem
equation
dy
dx
5
3x
2
1 2
2y 2 2
; yð0Þ5 y
0
;
the method of separation of variables results in the same
equation,
y
2
ðxÞ2 2yðxÞ5 x
3
1 2x;
when y
0
5 0 and when y
0
5 2. And yet, the solutions to the
two initial value problems clearly must differ. Explain
how this is possible.
49. According to Torricelli’s Law, if there is a hole of area a
at the bottom of a tank, then the volume V(t) and height
y(t) of water in the tank at time t are related by
dV
dt
52a
ffiffiffiffiffiffiffiffi
2gy
p
where g is equal to gravitational acceleration at Earth’s
surface. (Notice that the differential equation is dimen-
sionally correct—both sides bear units of L
3
/T where L is
length and t is time.) Use the Fundamental Theorem of
Calculus together with the Chain Rule to show that
AðyÞ
dy
dt
52a
ffiffiffiffiffiffiffiffi
2gy
p
:
50. A cubic tank filled with water has side length 1 m. At time
t 5 0, a circular hole of radius 4 cm opens up on the bot-
tom of the tank. If the proportionality constant k in
Torricelli’s Law is given by k 5 5/π m
1/2
/s, how long does
it take the tank to drain?
51. A tank in the shape of a conical frustum filled with water
is one meter deep at its central axis, has radius 2 m at its
top, and one meter at its bottom. At time t 5 0, a circular
hole of radius 1 cm opens up at the bottom. Suppose that
the proportionality constant k in Torricelli’s Law is given
by k 5 32/15 m
1/2
/s. Find an equation for the height y(t)of
water in the tank at time t. How long does it take the tank
to completely drain?
52. The escape velocity is the minimum initial velocity v
e
at
which a projectile launched straight up will never return
to Earth. Use equation (7.6.7) to find a formula for v
e
in
terms of g and R.
53. A population P(t) satisfies logistic growth equation (7.6.8)
with k 5 1/2 and P
N
5 2P
0
.AtwhattimeisP(t) 5 (3/2) P
0
?
54. A population P(t ) satisfies the logistic growth equation
P
0
ðtÞ5 α PðtÞ2 β P
2
ðtÞ for positive constants α and β.
What is the carrying capacity?
55. By completing the square on the right side of logistic
growth equation (7.6.8), show that a solution P(t) has
exactly one inflection point: (t
I
, P(t
I
)) where P(t
I
) 5 P
N
/2.
56. According to the preceding exercise, the solution P(t)to
logistic growth equation (7.6.8) has one inflection point,
(t
I
, P(t
I
)), where P(t
I
) 5 P
N
/2. Show that
t
I
5
1
kP
N
ln
P
N
2 P
0
P
0
:
57. Let P be the logistic growth function defined by equation
(7.6.10). Let t
I
be the time at which P has an inflection
point. (Refer to the two preceding exercises.) Show that
P(t) can be expressed in terms of the parameters k, P
N
,
and t
I
by means of the formula
PðtÞ5
P
N
1 1 exp
2k P
N
ðt 2 t
I
Þ
:
58. If a population is to be modeled by the logistic growth
function P defined by equation (7.6.10), then the three
parameters P
0
, k, and P
N
must be determined. It is easiest
to solve for these constants by measuring P(t) at equally
spaced times t
0
2 τ, t
0
, and t
0
1 τ. Having done so, we
position the origin of the time axis so that t 5 0 corre-
sponds to the time t
0
, then A 5 P(2τ), P
0
5 P(0), and
B 5 P(τ) are the measured population values.
a. Use the equation B 5 P(τ) to express exp(2k P
N
τ)
in terms of B, P
0
, and P
N
.
b. Use the equation A 5 P(2τ) to express exp(k P
N
τ)
in terms of A, P
0
, and P
N
.
c. The product of exp(2k P
N
τ) and exp(k P
N
τ)is1.
Use this observation together with parts a and b to
show that
P
N
5
ðA 1 BÞP
2
0
2 2ABP
0
P
2
0
2 AB
:
d. Use your formula from part b to show that
expð2k P
N
tÞ5
P
0
A
P
N
2 A
P
N
2 P
0
2t=τ
:
7.6 First Order Differential Equations—Separable Equations 601

e. Deduce that
PðtÞ5
P
0
P
N
P
0
1 ðP
N
2 P
0
Þ
P
0
A
P
N
2 A
P
N
2 P
0
2t=τ
:
59. A town’s population (in thousands) was 36 in 1980, 60 in
1990, and 90 in 2000. Assuming that the growth of the
population of this town is logistic, what will the popula-
tion be in the year 2020? (Use the preceding exercise.)
60. In Exercise 58, the logistic growth formula determined in
part e is obtained without solving for the growth constant
k in terms of the measured data A, P
0
, and B.
a. Use the formula in part d of Exercise 58 with t 5 τ to
obtain a formula for k.
b. Use the logistic growth equation to express k in terms
of the data P
0
, P
N
, and P
0
(0).
c. Assuming that τ is small, approximate k using part b
and the central difference approximation for the first
derivative.
61. The plot of the pumpkin data in Figure 6 has an inflection
point near (9, 25). For simplicity, let us use these coordi-
nates for the inflection point. The initial diameter P(0) is
3.6 cm. Using Exercises 55 and 56, find P
N
and k.
62. A population P satisfies the differential equation
P
0
ðtÞ5 10
25
PðtÞ
15000 2 PðtÞ
:
For what value P(0) of the initial population is the initial
growth rate P
0
(0) greatest?
63. When sucrose is dissolved in water, glucose and fructose
are formed. The reaction rate satisfies
d½C
12
H
22
O
11
dt
525:7 3 10
25
½C
12
H
22
O
11
:
For what value of t is the concentration of sucrose,
[C
12
H
22
O
11
], equal to 1/3 its initial value?
64. The chemical reaction
CH
3
COCH
3
1 I
2
- CH
3
COCH
2
I 1 HI
between acetone and iodine is governed by the differ-
ential equation
d½I
2
dt
520:41 3 10
23
½I
2
2
(in moles per liter per second). If the initial iodine con-
centration is c
0
, solve for [I
2
] as a function of time. Sup-
pose that [I
2
] is plotted as a function of time. What is the
slope of the graph when [I
2
] 5 1/10 mole/liter? Suppose
that 1/[I
2
] is plotted as a function of time. What is the
slope of the graph when [I
2
] 5 1/10 mole/liter?
65. In the decomposition of dinitrogen pentoxide,
N
2
O
5
- 2NO
2
1
1
2
O
2
;
the reaction rate satisfies the equation
d½N
2
O
5
dt
52k ½N
2
O
5
for some positive constant k.If[N
2
O
5
] is equal to 2.32
moles per liter when t 5 0 seconds and if [N
2
O
5
] is equal
to 0.37 moles per liter when t 5 3000 seconds, then what is
[N
2
O
5
] as a function of time?
66. The reaction rate of
2NO 1 H
2
- N
2
O 1 H
2
O
is given by
d½N
2
O
dt
5 0:44 3 10
26
ðh 2 ½N
2
OÞ
3
where h is the number of moles per liter of H
2
that are
initially present. What is the initial concentration of
[N
2
O]? Solve for [N
2
O] as an explicit function of t.In
doing so, you will need to extract a square root. Decide
which sign, 1 or 2 to use; explain your answer.What is
lim
t-N
½N
2
O?
67. Suppose that φ is a function of one variable. The differ-
ential equation dy/dx 5 φ( y/x) is said to be homogeneous
of degree 0. Let w( x) 5 y(x)/x. Differentiate both sides of
the equation y(x) 5 x w(x) with respect to x. By equating
the resulting expression for dy/dx with φ( y/x), show that
w(x) is the solution of a separable differential equation.
Illustrate this theory by solving the differential equation
dy/dx 5 2xy/(x
2
1 y
2
). For this example, φ(w) 5 2w/
(1 1 w
2
).
68. Suppose that ψ is a function of one variable and that a, b,
and c are constants. If dy/dx 5 ψ(a 1 bx 1 cy), then
show that u(x) 5 a 1 bx 1 cy(x) is the solution of a
separable equation. Illustrate by solving the equation
dy/dx 5 1 1 x 1 y.
69. The pressure P and temperature T in the outer envelope
of a white dwarf (star) are related by the differential
equation
dP
dT
5 C
T
7:5
P
; Pð0Þ5 0
where C is a constant. Find P as a function of T.
70. The interior temperature T
I
(in degrees K) of a cooling
white dwarf (star) satisfies the differential equation
dT
I
dt
52k
T
I
7 3 10
7
K
7=2
:
Here k is a constant with units degrees K per year, and t
represents time in years. Solve for T
I
.Ifk 5 6
K/yr and if
T
I
(0) 5 10
8
K, then in how many years will the star cool
to 10
4
K?
71. A spherical star of radius R is in equilibrium if the pres-
sure gradient dP/dr exactly opposes gravity. In the case of
Newtonian gravitation, this amounts to
602 Chapter 7 Applications of the Integral

dP
dr
52
GmðrÞρðrÞ
r
2
; PðRÞ5 0:
Here G is the gravitational constant, r represents distance
to the center, m(r) represents the mass of that part of the
star that is within distance r of the center, and ρ(r)repre-
sents the mass density at radius r.ComputeP(r) under the
assumption that the mass density is a constant ρ.Showthat
the pressure at the center of the star is 2πGρ
2
R
2
/3 (in terms
of the stellar radius R)or(π/6)
1/3
GM
2/3
ρ
4/3
(in terms of the
stellar mass M).
72. A bullet is fired into a sand pile with an initial speed of
1024 feet per second. The rate at which its velocity is
decreased after entering the sand pile is 500 times the
4
5
th
power of the velocity if units of feet and seconds are used.
How long is it before the bullet comes to rest?
73. Refer to the preceding exercise. How far does the bullet
travel in the sand before coming to rest?
74. The standard normal probability density f satisfies the
differential equation
f
0
ðxÞ52xf ðxÞ; f ð0Þ5
1
ffiffiffiffiffiffi
2π
p
:
Find f (x).
75. Suppose that, in a certain ecosystem, there is one type of
predator and one type of prey. Let x 100 denote the
number of predators and y 1000 denote the number
of prey. The Austrian mathematician A.J. Lotka
(18801949) and the Italian mathematician Vito Volterra
(18601940) proposed the following relationship, the
so-called Lotka-Volterra Equation, between the two
population sizes:
dy
dx
5
y ða 2 bxÞ
x ðcy 2 dÞ
:
Separate variables and solve this equation. What is the
predator-prey relationship if the initial prey population is
1500, the initial predator population is 200, and if a 5 6,
b 5 2, c 5 4, and d 5 7? Figure 11 illustrates the solution
curve of this Lotka-Volterra equation. Its potato-pancake
shape is typical.
76. Suppose that λ, A, and p are positive constants. Solve the
differential equation
dy
dt
5
λ
p
t
p21
ðA 2 yÞ:
A solution of this equation is known as a Janoschek
growth function. Such functions are often used to model
animal growth. The parameter A is called “the size of the
adult.” Why?
77. The Tractrix. The tip of a boat is at the point ( L, 0) on the
positive x-axis. Attached to the tip is a chord of length L.
A man starting at (0, 0) pulls the boat by the chord as he
walks up the y-axis. The chord is always tangent to the
path of the tip of the boat. Show that the position y(x)of
the tip of the boat is given by
dy
dx
52
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
L
2
2 x
2
p
x
; yðLÞ5 0:
The graph of y is called the tractrix (Figure 12).
78. Actuaries use mortality tables to show the expected
number of survivors of an initial group. Let L(x) denote
the number from that group who are living at age x. Then
2L
0
(x) is the instantaneous death rate and the percentage
rate, 2L
0
(x)/L(x) is called the force of mortality. The first
significant formula was derived by B. Gompertz assumed
that the force of mortality increases with age according to
an expression of the form Bg
x
for some constants B . 0
and g . 1. Solve for L(x) under Gompertz’s assumption.
79. M. W. Makeham emended Gompertz’s assumption for
the force of mortality to take into account accidental
deaths—refer to the preceding exercise for background.
Under Makeham’s assumption, the force of mortality has
the form M 1 Bg
x
for some positive constants M, B, and g
with g . 1. Solve for L(x) under this assumption. The
resulting formula is known as Makeham’s Law.
80. Du Nouy’s equation for the decreasing surface tension T
of blood serum is
Prey (in thousands)
Predators
(
in hundreds
)
2.0
2.4
2.0
1.6
1.2
2.5 3.0 3.5 4.0
m Figure 11 Solution of Lotka-Volterra equation
x
y
Man
Tractrix
Chord
(0, 0)
(
L, 0
)
Tip of boat
(x, y)
m Figure 12
7.6 First Order Differential Equations—Separable Equations 603

dT
dt
52k
T
ffiffi
t
p
for some constant k. Solve this equation if T 5 τ at t 5 0.
81. Let x and y be the measures of two body parts with
relative growth rates that are proportional to a common
factor Φ(t):
1
x
dx
dt
5 α ΦðtÞ and
1
y
dy
dt
5 β ΦðtÞ:
Show that x and y satisfy the Huxley Allometry Equation
y 5 kx
p
for suitable constants k and p.
82. The shape of a Bessel horn is determined by the equation
da
dx
52γ
a
x 1 x
0
where a(x) is the bore radius at distance x from the edge
of the bell of the horn, and x
0
and γ are positive constants.
Solve for a as a function of x. Determine a(x) for a
trumpet with γ 5 0.7, a(0) 5 10, and a(30) 5 2. Sketch the
graph of y 5 a (x) for 0 # x # 30.
83. Verify that yðxÞ5 expð2x
2
Þ
R
x
0
expðt
2
Þdt, which is known
as Dawson’s Integral, is the solution of the initial value
problem
dy
dx
5 1 2 2xy; y
0
5 0.
84. For each x . 0, there is a unique y . 0 such that ye
y
5 x.
Denote this value of y by W(x). Show that the function W
(called Lambert’s W function) is a solution of the differ-
ential equation
dy
dx
5
y
xð1 1 yÞ
:
85. Suppose an object of mass m is propelled upwards from
the surface of the earth with initial velocity v
0
. Suppose
that the (downward) force of air resistance R(v) is pro-
portional to the square of the speed: R(v) 52k v
2
, where
k is a positive constant that carries the units of mass/
length. (This is the quadratic drag law.) Solve the initial
value problem for motion:
m
dv
dt
52kv
2
2 mg; vð0Þ5 v
0
:
86. Suppose that the force R of air resistance on a 0.2 kg
object thrown straight up with initial velocity 28 m/s is
given by the quadratic drag law,
RðvÞ52kv
2
;
where k 5 4 3 10
26
kg/m. Find an equation for the time τ
at which the object begins to fall.
87. Let v(t) denote the velocity at time t of an object of mass m
that is dropped from a positive height at time t 5 0. Assume
that, throughout its fall, the (upward) force of air resistance
on the object can be approximated by the formula
R(v) 51k v
2
,wherek is a positive constant that carries
the units of mass/length. (As in Exercises 85 and 86, this
equation is the quadratic drag law. Because drag is in the
opposite direction of motion, the sign for upward motion
is opposite to that for downward motion.) Show that
vðtÞ5
ffiffiffiffiffiffiffi
mg
k
r
tanh
2t
ffiffiffiffiffi
kg
m
r
until impact.
88. The rate of elimination of alcohol from the bloodstream is
proportional to the amount A that is present. That is,
dA
dt
52
1
k
A;
where k is a time constant that depends on the drug and
the individual. If k is 1/2 hour for a certain person, how
long will it take for his blood alcohol content to reduce
from 0.12% to 0.06%?
89. A column of air with cross-sectional area 1 cm
2
extends
indefinitely upwards from sea level (i.e. to infinity). The
atmospheric pressur e p at height y above sea level is the
weight of that part of this infinite column of air that extends
from y to infinity. Assume that the density of the air is
proportional to the pressure. (This is an approximation that
follows from Boyle’s law, assuming constant temperature.)
Show that there is a positive constant k such that
dp
dy
52kp:
Under this model, what is the mathematical expression
for atmospheric pressure? What physical dimensions does
K carry?
90. Suppose that α and β are positive constants. The differ-
ential equation
P
0
ðtÞ5 α e
2βt
PðtÞ
for a positive function P is known as the Gompertz growth
equation. (It is named for Benjamin Gompertz (17791865),
a self-educated scholar of w ide-ranging interests.) Find an
explicit formula for P(t). Use your explicit solution to show
that there is a number P
N
(known as the carrying capacity)
such that
lim
t-N
PðtÞ5 P
N
:
Show that the Gompertz growth equation may be written
in the form
P
0
ðtÞ5 k PðtÞln
P
N
PðtÞ
:
91. In forestry, the function EðTÞ5 C e
αT=ðT1βÞ
has been
used to model water evaporation as a function of tem-
perature T. Here α and β are constants with α . 2 and
β . 0. Show that
E
0
ðTÞ5
αβ
ðT 1 βÞ
2
EðTÞ
604 Chapter 7 Applications of the Integral
