Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


THEOREM 1
Let f be a continuous nonnegative function on the interval [a, b].
Let R denote the region bounded above by the graph of y 5 f(x), below by the
x-axis, and on the sides by the line segments x 5 a and x 5 b. Let M denote the
mass of R.IfR has a uniform mass de nsity δ, then the x-coordinate
x of the
center of mass of R is given by
x 5
M
x50
M
5
R
b
a
xf ðxÞdx
R
b
a
f ðxÞdx
; ð7:4:6Þ
and the y-coordinate
y of the center of mass of R is given by
y 5
M
y50
M
5
1
2
R
b
a
f ðxÞ
2
dx
R
b
a
f ðxÞdx
: ð7:4:7Þ
Proof. By
definition, M
x5x
5 0. To determine x, we solve for x in the equation
δ
R
b
a
ðx 2 xÞf ðxÞdx 5 0. After expanding the integrand and expressing the resulting
integral as a sum, we obtain
δ
Z
b
a
xf ðxÞdx 2 x δ
Z
b
a
f ðxÞdx 5 0:
Solving for
x, we find that
x 5
R
b
a
xf ðxÞdx
R
b
a
f ðxÞdx
5
M
x50
M
:
Notice that the uniform mass density δ has been eliminated and does not appear in
the final formula for
x.
The equation y 5 M
y50
/M is obtained analogously. Into this equation, we
substitute the value for M
y50
given by formula (7.4.5). The second quotient of line
(7.4.7) is the result. ’
⁄ EX
AMPLE 3 Let R be
the region bounded by the lines y 5 x 2 1, y 5 0,
and x 5 6 (as in Example 1). Suppose that R has uniform mass density δ 5 2 (as in
Example 1). Calculate the center of mass of R.
Solution In
Example 1, we calculated M
x50
5 325/3. The total mass M of R is
computed as follows:
M 5 δ
Z
6
1
ðx 2 1Þdx 5 2
1
2
x
2
2 x
6
1
5 25:
Therefore
x 5
325 =3
25
5
13
3
:
In Example 2, we showed that M
y50
5 125/3. Therefore
y 5
125 =3
25
5
5
3
:
Thus the center of mass is (13/3, 5/3).
¥
7.4 Center of Mass 575
The next theorem generalizes formulas (7.4.6) and (7.4.7) by removing the
requirement that the lower boundary of R be the x-axis.
THEOREM 2
Let f and g be continuous functions on the interval [a, b] with g(x)
for all x in [a, b]. Let R denote the region bounded above by the graph of
y 5 f(x), below by the graph of y 5 g(x), and on the sides by the line segments
x 5 a and x 5 b.IfR has uniform mass density, then the x-coordinate
x of the
center of mass of R is given by
x 5
R
b
a
x
f ðxÞ2 gðxÞ
dx
R
b
a
f ðxÞ2 gðxÞ
dx
: ð7:4:8Þ
The y-coordinate
y of the center of mass of R is given by
y 5
1
2
R
b
a
f ðxÞ
2
2 gðxÞ
2
dx
R
b
a
f ðxÞ2 gðxÞ
dx
: ð7:4:9Þ
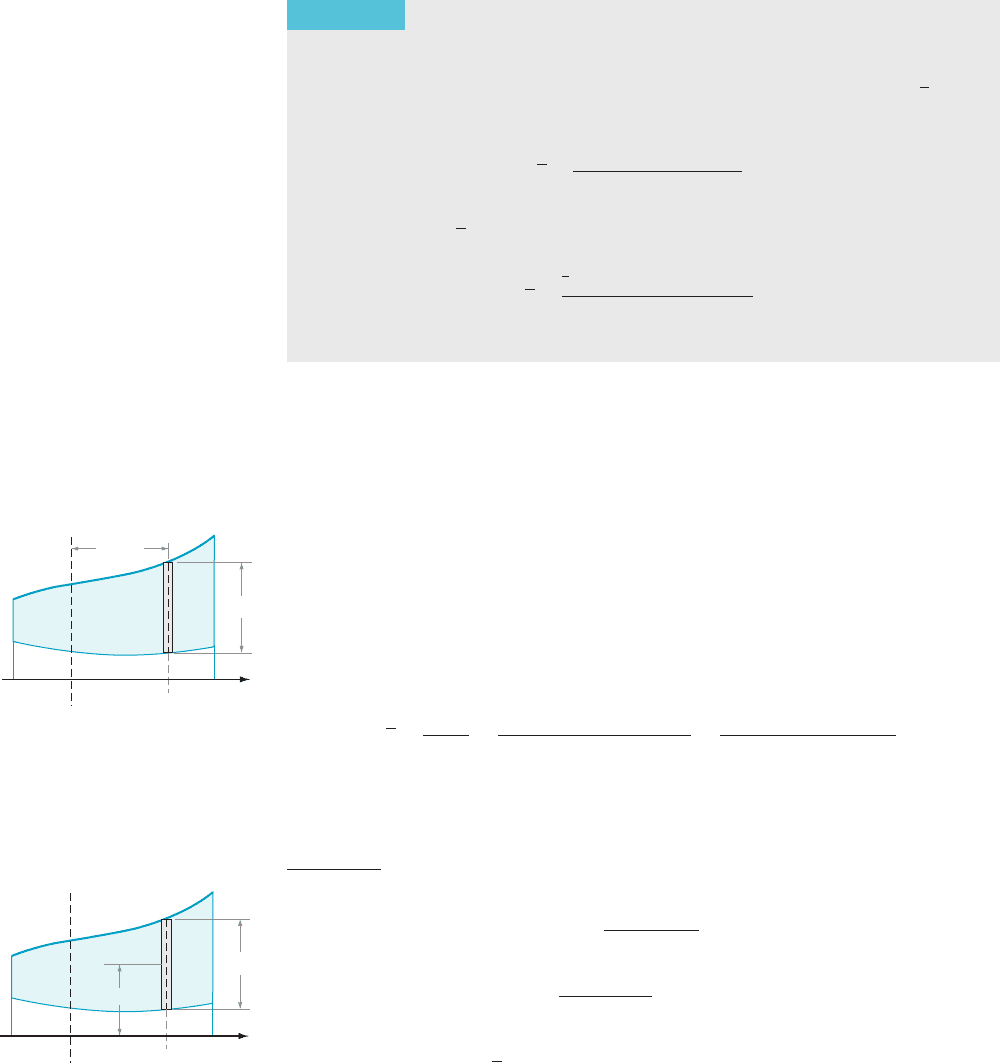
Proof. Let Δx den
ote the common length of the subintervals that result from the
uniform partition a 5 x
0
, x
1
, ..., x
N
5 b of the interval [a, b]. Let s
j
be the
midpoint of the j
th
subinterval I
j
. The height of the thin rectangle shown in Figure 9
is f (s
j
) 2 g(s
j
), its area is ( f ( s
j
) 2 g(s
j
))Δx, its mass is δ( f (s
j
) 2 g(s
j
))Δx, and its
moment about the y-axis is δs
j
( f (s
j
) 2 g(s
j
))Δx. The total moment resulting from
the partition is therefore
P
N
j51
δ s
j
f ðs
j
Þ2 gð s
j
Þ
Δx. It follows that
M
x50
5 lim
N-N
X
N
j51
δ s
j
f ðs
j
Þ2 gð s
j
Þ
Δx 5 δ
Z
b
a
x
f ðxÞ2 gð x Þ
dx:
Also, the mass M of R is the product of δ and the area of R,orδ
R
b
a
f ðxÞ2 gð x Þ
dx.
Thus
x 5
M
x50
M
5
δ
R
b
a
x
f ðxÞ2 gðxÞ
dx
δ
R
b
a
f ðxÞ2 gðxÞ
dx
5
R
b
a
x
f ðxÞ2 gðxÞ
dx
R
b
a
f ðxÞ2 gð x Þ
dx
:
To calculate the mom ent of the thin rect angle about the x-axis, we form the pro-
duct of the mass δ
f ðs
j
Þ2 gðs
j
Þ
Δx of the rectangle and the average distance,
f ðs
j
Þ1 gðs
j
Þ
2
, of points of the rectangle to the x-axis. See Figure 10. Thus
M
y50
5 lim
N-N
X
N
j51
δ
f ðs
j
Þ1 gðs
j
Þ
2
f ðs
j
Þ2 gðs
j
Þ
Δx
5 δ
Z
b
a
f ðxÞ1 gðxÞ
2
f ðxÞ2 gðxÞ
dx
5
δ
2
Z
b
a
f ðxÞ
2
2 gðxÞ
2
dx
and
a
b
x c
y f(x)
f(s
j
)g(s
j
)
c
s
j
x
j
x
j1
s
j
c
x
m Figure 9
a
b
x c
y f(x)
f(s
j
)g(s
j
)
c
s
j
x
j
x
j1
(f(s
j
)g(s
j
))
x
m Figure 10
576 Chapter
7 Applications of the Integral
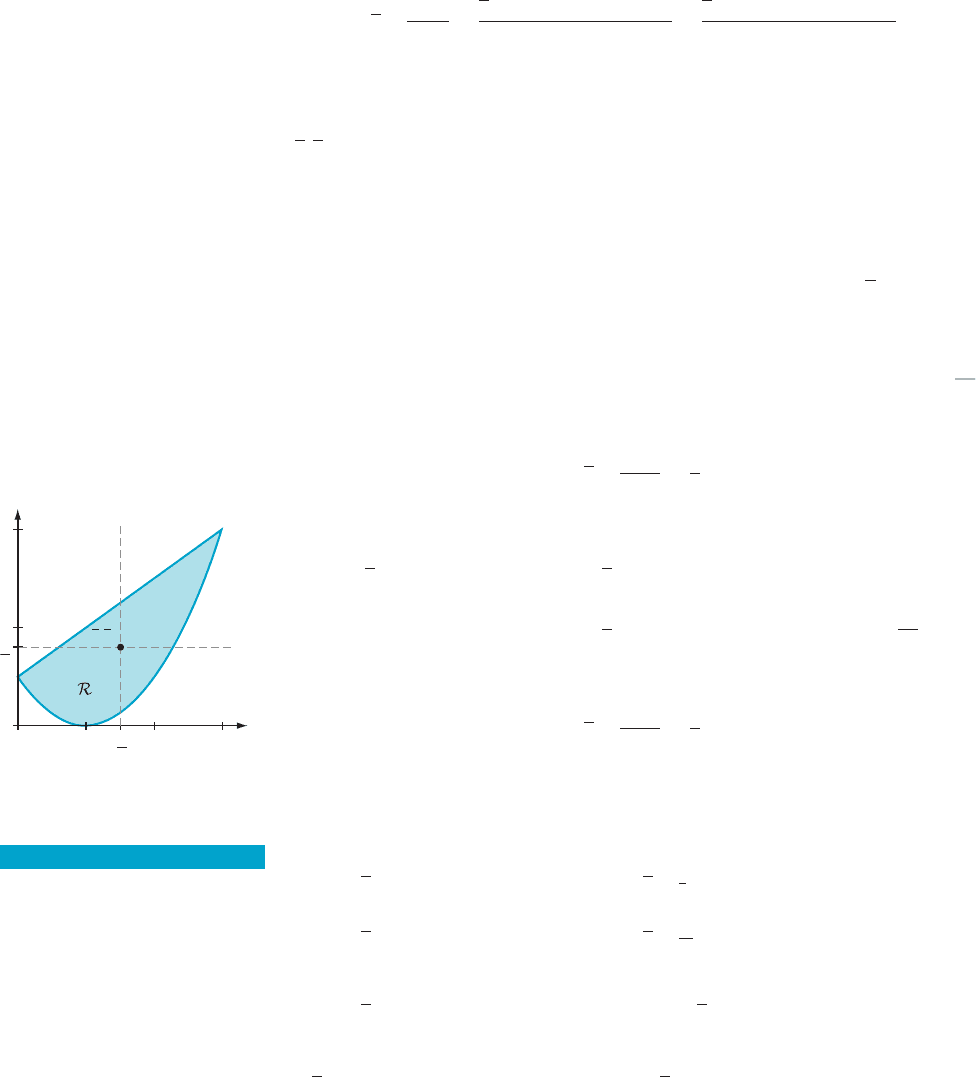
y 5
M
y50
M
5
δ
2
R
b
a
f ðxÞ
2
2 gðxÞ
2
dx
δ
R
b
a
f ðxÞ2 gðxÞ
dx
5
1
2
R
b
a
f ðxÞ
2
2 gðxÞ
2
dx
R
b
a
f ðxÞ2 gðxÞ
dx
: ’
⁄ EX
AMPLE 4 Let R be
the region bounded above by y 5 x 1 1 and be low
by y 5 (x 2 1)
2
. Suppose that R has unit mass density. What is the center of mass
(
x, y)ofR?
Solution The
two graphs intersect when x 1 1 5 (x 2 1)
2
,orx 1 1 5 x
2
2 2x 1 1, or
3x 5 x
2
. The solutions are x 5 0 and x 5 3. Next, we set f (x) 5 x 1 1andg(x) 5
(x 2 1)
2
and calculate
Z
3
0
f ðxÞ2 gð x Þ
dx 5
Z
3
0
ðx 1 1Þ2 ðx 2 1Þ
2
dx 5
9
2
:
The numerator of formula (7.4.8) is
Z
b
a
x
f ðxÞ2 gð x Þ
dx 5
Z
3
0
x
ðx 1 1Þ2 ðx 2 1Þ
2
dx 5
Z
3
0
ð3x
2
2 x
3
Þdx 5
27
4
:
Therefore
x 5
27=4
9=2
5
3
2
:
The numerator of formula (7.4.9) is
1
2
Z
b
a
f ðxÞ
2
2 gðxÞ
2
dx 5
1
2
Z
3
0
ðx 1 1Þ
2
2 ðx 2 1Þ
4
dx
5
1
2
Z
3
0
ð2x
4
1 4x
3
2 5x
2
1 6xÞdx 5
36
5
:
Therefore
y 5
36=5
9=2
5
8
5
:
The center of mass of R is (3/2, 8/5). See Figure 11.
¥
QUICK QUIZ
1. Let R denote the triangle with vertices (0, 0), (2, 0), and (2, 6). The x-center of
mass
x of R is given by the equation x 5
1
6
R
2
0
gðxÞdx for what function g(x)?
2. Let R denote the triangle with vertices (0, 0), (2, 0), and (2, 6). The x-center of
mass
y of R is given by the equation y 5
1
12
R
2
0
gðxÞdx for what function g(x)?
3. Let R denote the part that is bounded above by y 5 2/x, below by y 5 1/x, on the
left by x 5 1, and on the right by x 5 2. The area of R is ln(2). The x-center of
mass
x of R is given by the equation ln(2) x 5 α for what value of α?
4. Let R denote the part that is bounded above by y 5 2/x, below by y 5 1/x,onthe
left by x 5 1, and on the right by x 5 2. The area of R is ln(2). The y-center of mass
y of R is given by the equation 4 lnð2Þy 5
R
2
1
gðxÞdx for what function g(x)?
Answers
1. 3x
2
2. 9x
2
3. 1 4. 3/x
2
4
2
0
1233
2
8
5
y x 1
y
y (x 1)
2
(x,y)
x
m Figure 11
7.4 Center of Mass 577

EXERCISES
Problems for Practice
c In each of Exercises 128, find the moment of the given
region R about the given vertical axis. Assume that R has
uniform unit mass density. b
1. R is
the triangular region with vertices (0, 0), (0, 2), and
(6, 0); about x 5 3.
2. R is the triangular region with vertices (0, 0), (0, 2), and
(6, 0); about x 521.
3. R is the triangular region with vertices (0, 0), (0, 2), and
(6, 0); about x 5 2.
4. R is the first quadrant region bounded by y 5 4x 2 x
3
and
the x-axis; about x 5 1.
5. R is the first quadrant region bounded by y 5 4x 2 x
3
and
the x-axis; about x 5 3.
6. R is the first quadrant region bounded above by y 5 x 2 x
2
and the x-axis; about x 5 0.
7. R is the region bounded above by y 5 1/x, below by the x-
axis, and on the sides by the vertical lines x 5 1 and x 5 2;
about x 523.
8. R is the first quadrant region bounded above by y 5
sinðxÞ
x
,
below by the x-axis, and on the sides by x 5 π/6 and x 5 π/2;
about x 5 0.
c In each of Exercises 9216, find the moment of the given
region R about
the x-axis. Assume that R has uniform unit
mass density. b
9. R is
the triangular region with vertices (0, 0), (0, 2), and
(6, 0).
10. R is the first quadrant region bounded above by y 5
ffiffiffi
x
p
,
below by the x-axis, and on the right by x 5 4.
11. R is the region bounded above by y 5 1/x, below by the x-
axis, and on the sides by the vertical lines x 5 1 and x 5 2.
12. R is the first quadrant region bounded above by y 5 e
x
,
below by the x-axis, and on the sides by x 5 1 and x 5 2.
13. R is the region bounded above by y 5
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
and below
by the x-axis.
14. R is the first quadrant region bounded above by
y 5 1 2 x
3
and below by the x-axis.
15. R is the first quadrant region bounded above by
y 5
ffiffiffi
x
p
ð1 2 x
2
Þ
2
and below by the x-axis.
16. R is the first quadrant region bounded above by
y 5 6x=ð1 1 x
3
Þ, below by the x-axis, and on the right by
x 5 1.
c In each of Exercises 17228, find the center of mass (
x, y)of
the given region R, assuming that it has uniform mass density. b
17. R is
the triangular region with vertices (0, 0), (0, 2), and
(6, 0).
18. R is the region bounded by y 5 4 2 x
2
and the x-axis.
19. R is the first quadrant region bounded above by
y 5
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
and below by the x-axis.
20. R is the region bounded above by y 5 cos(x), 0 # x # π/2,
and below by the x-axis.
21. R is the region bounded above by y 5 8 2 2x 2 x
2
and
below by the x-axis.
22. R is the region bounded by y 5 x 2 x
3
,0# x # 1, and the
x-axis.
23. R is the region bounded by y 5 1/x,1# x # 2, and the
x-axis.
24. R is the region bounded by y 5
ffiffiffi
x
p
; x 5 4; x 5 9; and the
x-axis.
25. R is the region bounded above by y 5 e
x
, below by the
x-axis, on the left by x 5 0, and on the right by x 5 1.
26. R is the region bounded by y 5 1=
ffiffiffi
x
p
; 4 # x # 9, and the
x-axis.
27. R is the region bounded above by y 5 1=
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
, below
by the x-axis, on the left by x 5 0, and on the right by
x 5 1=
ffiffiffi
2
p
.
28. R is the region bounded by y 5 x 1 1/x, x 5 1/2, x 5 2, and
the x-axis.
c In each of Exercises 29236, find the center of mass (
x, y)
of the given region R, assuming that it has uniform unit mass
density. b
29. R is
the region bounded above by y 5 4(1 2 x
2
) and below
by y 5 1 2 x
2
.
30. R is the region bounded above by y 5 2x and below by
y 5 x
2
.
31. R is the region bounded above by y 5 2
ffiffiffi
x
p
and below by
y 5 x.
32. R is the region bounded above by y 5 x, below by y 5
ffiffiffi
x
p
,
on the left by x 5 1, and on the right by x 5 4.
33. R is the region bounded above by y 5 x 1 5, below by
y 5 4 2 x
2
, on the left by x 521, and on the right by x 5 2.
34. R is the region bounded above by y 5 5 2 x, below by
y 5
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
, and on the left by x 5 0.
35. R is the region bounded above by y 5 2, below by
y 5
ffiffiffiffiffiffiffiffiffiffiffi
4 2 x
p
, and on the right by x 5 3.
578 Chapter 7 Applications of the Integral

36. R is the region bounded above by y 5 2(1 1 x
2
), below by
y 5 1 2 x
2
, on the left by x 5 0, and on the right by x 5 1.
Further Theory and Practice
c In each of Exercises 37244, find the center of mass of the
given region R, assuming that it has uniform unit mass
density. b
37. R is the region bounded above by y 5 cos(x)for0# x # π/2,
below by the x-axis,andontheleftbyx 5 0.
38. R is the region bounded above by y 5 ln(x), below by the
x-axis, and on the sides by x 5 1 and x 5 e.
39. R is the region bounded above by y 5 1/(1 1 x
2
), below by
the x-axis, and on the sides by x 5 0 and x 5 1.
40. R is the region bounded above by y 5 x=
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 2x
2
p
, below
by the x-axis, and on the sides by x 5 0 and x 5 2.
41. R is the region bounded above by y 5 (1 2 x
2
)
3/2
and
below by the x-axis.
42. R is the region bounded above by y 5 (16 1 x
2
)
21/2
, below
by the x-axis, on the left by x 5 0, and on the right by
x 5 3.
43. R is the region bounded above by y 5 x 2 1/x, below by
the x-axis, on the left by x 5 1, and on the right by x 5 2.
44. R is the region in the first quadrant that is bounded above
by y 5 x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
and below by the x-axis.
c In each of Exercises 45252, find the center of mass of the
given
region R, assuming that it has uniform unit mass
density. b
45. R is
the region bounded above by y 5 1 for 21 # x # 0
and by y 5 1 2 x for 0 # x # 1, below by the x-axis, and on
the left by x 521.
46. R is the region bounded above by y 5 1 1 |x|(21 # x # 2),
below by the x-axis, and on the sides by x 521 and x 5 2.
47. R is the region bounded above by y 5 4 2 x
2
for
22 # x # 1, below by y 5 3x for 0 # x, and below by the x-
axis for x , 0.
48. R is the region bounded above by y 5 3x for 0 # x # 1,
above by y 5 4 2 x
2
for 1 # x # 2 and below by the x-axis.
49. R is the region bounded above by y 5 2 2 x
2
, below by
y 52x for 21 # x # 0, and below by y 5
ffiffiffi
x
p
for 0 # x # 1.
50. R is the region bounded above by
y 5
x
2
if 0 # x # 2
4ðx 2 3Þ
2
if 2 # x # 3
and below by the x-axis.
51. R is the region bounded above by y 5 2(1 1 |x|) for
21 # x # 4, below by y 5 (x 2 1)
2
for 21 # x # 4, and on
the right by x 5 4.
52. R is the region bounded above by y 5
ffiffiffiffiffiffiffiffiffiffiffi
x 1 2
p
for
22 # x # 2, below by the x-axis for 22 # x # 1, and below
by y 5 2
ffiffiffiffiffiffiffiffiffiffiffi
x 2 1
p
for 1 # x # 2.
53. Suppose that f is the probability density function of a
random variable X on an interval [a, b]. Let
x be the x-
coordinate of the center of mass of the region R bounded
above by the graph of f, below by the x-axis, and on the
sides by x 5 a and x 5 b.AssumingthatR has uniform unit
mass density, what is the relationship between
X and x?
c The moments M
x5c
5
R
b
a
ðx 2 cÞf ðxÞdx that have been
defined in this section are first moments.Iff is a continuous
function on [a, b], then the second moment of f about the
vertical axis x 5 c is defined to be I
x5c
5
R
b
a
ðx 2 cÞ
2
f ðxÞdx.
Second moments are used in moment of inertia calculations in
engineering and physics. In Exercises 54257, calculate the
se
cond moment of the given function f about the vertical axis
x 5 c for the given c. b
54. f ðxÞ5 1 1
ffiffi
ffi
x
p
1 # x # 4 c 5 0
55. f ðxÞ5 x
2
1 # x # 2 c 521
56. f ðxÞ5 x
3
1 1 21 # x # 2 c 5 1
57. f ðxÞ5 sinðxÞ 0 # x # π c 5 2π
c Second moments, as defined in the instructions to Exer-
cises 54257,
are used throughout probability and statistics. If
f is the probability density function of a random variable X
with range [a, b] and mean μ
X
, then the variance Var(X)ofX
is defined to be the second moment of f about the vertical axis
x 5 μ
X
:
VarðXÞ5
Z
b
a
ðx 2 μ
X
Þ
2
f ðxÞdx
Notice that 0 # Var(X) because (x 2 μ
X
)
2
and f (x) are both
nonnegative. The standard deviation σ
X
of X is defined by
σ
X
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
VarðXÞ
p
. (As a result, the variance is also denoted by σ
X
2
.)
In each of Exercises 58261, calculate the variance Var(X)o
fa
random variable X whose probability density function is the
given function f. b
58. f ðxÞ5 x=41# x # 3
59. f ðxÞ5 3x
2
0 # x # 1
60. f ðxÞ5 8=ð3x
3
Þ 1 # x # 2
61. f ðxÞ5 1=ðb 2 aÞ a # x # b
c In Exercises 62265, refer to the instructions for Exercises
5861
for the definition of Var(X). b
62. Let p b
e a positive constant. Suppose that a random variable
X has probability function f (x) 5 cx
p
(1 2 x)for0# x # 1.
Find formulas for c, μ
X
,andVar(X)intermsofp.
63. If X is a random variable with values in [a, b] and prob-
ability density function f, then X
2
is a random variable
and EðX
2
Þ5
R
b
a
x
2
f ðxÞdx. Use this fact to deduce that
Var(X) 5 E(X
2
) 2 E(X)
2
.
64. Suppose that 0 , λ and f (x) 5 λexp(2λx), 0 # x ,Nis the
probability density function of a random variable X.
Calculate μ
X
and Var(X).
7.4 Center of Mass 579
65. Suppose that μ is a real number and 0 , σ. It can be
shown that
f ðxÞ5
1
ffiffiffiffiffiffi
2π
p
σ
exp
2
1
2
x 2 μ
σ
2
; 2N # x # N
is the probability density function of a random variable X.
Show that μ 5 E(X) and σ
2
5 Var(X).
Calculator/Computer Exercises
c In Exercises 66270, find the center of mass of the given
region R. b
66. R is
bounded above by y 5 6x/exp(x) 2 1 and below by
the x-axis.
67. R is bounded above by y 5 1 1 x and below by y 5 exp(x
2
).
68. R is bounded above by y 5 4 1 2x 2 x
4
and below by
y 5 x 2 1.
69. R is bounded above by y 5 ln(1 1 x 1 x
2
) and below by
y 5 x
2
2 3.
70. R is bounded above by y 5 arctan(x
3
) and below by
y 5 x
2
1 x 2 4.
71. The equation of the Gateway Arch is
y 5 693:8597 2 34:38365
expðkxÞ1 expð2kxÞ
for k 5 0.0100333 and 2299.2239 , x , 299.2239. Find the
center of mass for the region that lies above the x-axis and
below this curve.
7.5 Work
Suppose that a body is moved a distance d along a straight line while being acted on
by a force of constant magnitude F in the direction of motion (Figure 1). Then, by
definition, the work performed in this move is force times distance:
W 5 F d: ð7:5:1Þ
Bear in mind that this is a technical definition of work that differs somewhat from
everyday usage. For example, a person has to exert a force of 100 pounds to hold up
a 100-pound weight. This may be a strain, and the pe rson may tire from the
exertion—but if the weight does not move, then no work is done.
If we graph the constant function F as in Figure 2, then we see that work is
related to area. When we think of area under a graph, however, the dist ance from 0
to 1 on each coordinate axis represents a unit length. The unit used to express area
must represent (length)
2
. The square- foot and square-meter are examples. In
contrast, it is evident from formula (7.5.1) that a unit of work must represent the
product of a force and a length. In Figure 2, the unit of measurement along the
vertical axis is a unit of force, not length.
Any combination of units that represents force 3 distance or, breaking it down
into basic components, mass 3 distance
2
can be used to represent work. However,
the unit of work can be expressed most simply by consistently using units from one of
three systems of measurement. In the United States customary system, the standard
unit of force is the pound (abbreviated lb). This leads to the foot-pound (ft-lb) as
the unit of measure for work: it is the amount of work done when a constant force
of one pound is applied for one foot. In the mks system of measurement, force is
measured in newtons (N) and distance is measured in meters (m). The unit of work
is the newton-meter, which is also called the joule(J): 1 joule is the amount of work
done when a constant force of 1 newton is applied for 1 meter. In the cgs system,1erg is
the amount of work done by a force of one dyne acting over a distance of 1 centimeter.
Also, 1 joule is equal to 10
7
ergs and approximately 0.73756215 foot-pounds.
Using Integrals to
Calculate Work
Suppose that a body is being moved from x 5 a to x 5 b along the x-axis and that
the force applied in the direction of motion at the point x is F(x) (see Figure 3).
ab
d
F
m Figure 1
Force
Distance
F ⴢ d
F
ab
d
m Figure 2
a
b
F(x)
x
m Figure 3
580 Chapter
7 Applications of the Integral

How much work is done altogether? If F is not a constant function, then formula
(7.5.1) cannot be applied. Instead, we examine this problem by partitioning the
interval into N subintervals of equal length Δx.IfΔx is sufficiently small, then F(x)
will not vary greatly over each subinterval of the partition. In other words, if s
j
is
any point in the j
th
subinterval, then the force applied throughout the j
th
subinterval
may be approximated by the constant force F(s
j
). The work done in the incremental
move over the j
th
subinterval is therefore about F(s
j
) Δx (Figure 4). Summing over
j, we obtain an approximation to the total work:
W
X
N
j 51
Fðs
j
ÞΔx: ð7:5:2Þ
As N increases and Δ x becomes smaller, approximation (7.5.2) becomes more
accurate. Notice that these approximating sums are also Riemann sums for the
integral
R
b
a
FðxÞdx: From Chapter 5, we know that these Riemann sums tend to the
integral as the number N of subintervals tends to infinity. We conclude that
R
b
a
FðxÞdx equals the total work. Observe that there is again an analogy between
work and area under the force curve.
DEFINITION
Suppose that a body is moved linearly from x 5 a to x 5 b by a
force in the direction of motion. If the magnitude of the force at each point x 2
[a, b]isF(x ), then the total work W performed is
W 5
Z
b
a
FðxÞdx: ð7:5:3Þ
Examples with Weights
That Vary
Newton’s Law, force equals mass times acceleration,orF 5 m a, tells us that weight
and mass are proportional if acceleration remains constant. If for some reason the
mass of a load decreases, as in the first example, then the weight of the load decreases.
⁄ EX
AMPLE 1 A man carries a leaky 50 pound sack of sand straight up a 100
foot ladder that runs up the side of a building. He climbs at a constant rate of 20
feet per minute. Sand leaks out of the sack at a rate of 4 pounds per minute.
Ignoring the man’s own weight, how much work does he perform on this trip?
Solution The
definition of work that is given previously is applicable whenever a
force is applied along a straight line—it does not matter if the line is horizontal or
vertical (or any other). The force that the man applies is the weight of the sack,
which, because of the leak, is not constant. Let F( y) denote the weight of the sack
of sand when the man is y feet above the ground. Because the man is y 5 20t ft
above the ground at time t when t is measured in minutes, and because the weight
of the sack is 50 2 4t lb when t is measured in minutes, we have
FðyÞ5 50 2 4
y
20
5 50 2
y
5
lb:
The total work that is performed therefore eq uals
W 5
Z
100
0
50 2
y
5
dy 5
50y 2
y
2
10
y5100
y50
5 4000 ft-lb:
y
F
x
F(s
j
)
s
j
x
ab
m Figure 4
7.5 Work 581

INSIGHT
Suppose that we did not ignore the man’s weight in Example 1. If he
weighs 200 pounds, then he has to lift his own weight when climbing the ladder also. In
this case, the work performed is
W 5
Z
100
0
50 2
y
5
1 200
dy
5
Z
100
0
50 2
y
5
dy 1
Z
100
0
200 dy
5 4000 1 200 100
5 24000 ft-lb:
At the surface of Earth, acceleration due to gravity is denoted by g and is equal
to 9.80665 m/s
2
in the mks system of measurement. The force needed to lift a mass
m is therefore F 5 mg at
Earth’s surface. Near the surface of Earth, we may con-
tinue to use the equation F 5 mg as an acceptable approximation to the weight-
mass relationship. That is why we are able to treat the weight of the man as
constant in the Insight to Example 1. In the next example, the distance from the
surface of Earth becomes so great that the assumption of constant gravitational
acceleration is not acceptable.
⁄ EXAMPLE 2 According to Newton’s Law of Gravitation, the magnitude of
the
gravitational force F (measured in newtons) exerted by Earth on a mass m
(measured in kilograms) is
F 5 3:98621 3 10
14
m
r
2
ð7:5:4Þ
when the mass is a distance r (measured in meters) from the center of Earth.
Determine how much work is performed in lifting a 5000 kilogram rocket to a
height 200 kilometers above the surface of the earth, assuming that the direction of
the force, as well as the motion, is straight up. Use 6375.58 km for the radius of
Earth.
Solution We
convert all units to the mks system. By doing so, we will arrive at a
value of work that is measured in joules. Because r 5 6375580 m at the surface of
the earth and r 5 6375580 1 200000 m, or r 5 6575580 m, when the rocket is 200 km
above the surface of the earth, we have
W 5
Z
6575580
6375580
FðrÞdr
5
Z
6575580
6375580
3:98621 3 10
14
5000
r
2
dr
523:98621 3 10
14
5000
r
r56575580
r56375580
523:98621 3 10
14
5000
1
6575580
2
1
6375580
5 9:50838 3 10
9
J: ¥
582 Chapter 7 Applications of the Integral

INSIGHT
At the surface of Earth, r equals 6375580 meters, and, for this value of r,
equation (7.5.4) becomes F 5 mg with g 5 9.80665 m/s
2
. At the top of Mount Everest,
r equals 6375580 1 8848, or r 5 6384428. Because (6375580/6384428)
2
5 0.997...,formula
(7.5.4) tells us that an object weighs about 0.3% less at the summit of Everest than at the
surface of Earth. A similar calculation shows that, when the rocket is 200 kilometers
above the surface of Earth, its weight is only 94% of its weight on Earth.
An Example Involving a
Spring
Consider a spring attached to a rigid support with one free end, as in Figure 5a.
According to Hooke’s Law, the force F that the spring exerts is proportional to the
amount that it has been extended or compressed. Although Hooke’s Law is not an
exact physical law, it is a very good approximation for small extensions and com-
pressions. When working problems with springs, it is usually convenient to set up a
coordinate axis with the origin at the free end of the relaxed spring, a point which is
sometimes called the equilibrium position. Let x denote the coordinate of the free
end of the spring. Then x represents the amount of extension when x . 0 and the
amount of compression when x , 0 . Hooke’s Law may be written as
F 52kx ð7:5:5Þ
for a positive constant k (known as the spring constant). The negative sign in Hooke’s
Law is required to reflect the direction of the force. It is a restorative force in that it is
always directed toward the equilibrium position. Thus when the spring is extended
and x . 0, the force is directed toward the negative x-axis (Figure 5b). When the
spring is compressed and x , 0, the force is directed toward the positive x-axis
(Figure 5c). Because the left side of equation (7.5.5) carries a unit of force (such as
pound or newton), so does the right side. It follows that the constant k carries units of
force divided by length. The spring constant therefore represents a stiffness density.
To stretch or compress a spring, a force must be exerted that is equal in
magnitude to the restorative spring force but opposite in direction. It follows from
Theorem 1 that, if 0 , a , b, then the work done in stretching a spring from a to b is
W 5
Z
b
a
kx dx:
⁄ EX
AMPLE 3 If 5 J work is done in extending a spring 0.2 m beyond its
equilibrium position, then how much additional work is required to extend it a
further 0.2 m?
Solution We
first use the given information to solve for the spring constant:
5J 5
Z
0:2m
0m
kx dx 5
1
2
kx
2
x50:2m
x50m
5 0:02k m
2
or
k 5
5
0:02
Jm
22
5 250 N mm
22
5 250 Nm
21
:
Finally, the required work W is calculated as follows:
W 5
Z
0:4m
0:2m
kx dx 5
1
2
kx
2
x50:4m
x50:2m
5
1
2
kð0:4
2
m
2
2 0:2
2
m
2
Þ5 0:06k m
2
:
Equilibrium or rest position
0
m Figure 5a Spring at rest
0
x
m Figure 5b Stretched spring
(x . 0)
0
x
m Figure 5c Compressed spring
(x . 0)
7
.5 Work 583
We obtain our final answer by substituting in the value for the spring constant:
W 5 ð0:06Þð250 N m
21
Þm
2
5 15 N m 5 15 J: ¥
Examples that Involve
Pumping a Fluid from a
Reservoir
The analysis that results in the definition of work as an integral can be used to solve
a variety of problems. Until now, we have considered examples that concern a
variable force. In our next application, pumpi ng a fluid to the top of a reservoir, it is
the distance that varies because the fluid at each horizontal level must be raised a
distance equal to its depth. In the two examples that follow, we will need the weight
density of water: 9806.65 newtons per cubic meter in the mks system and 62.428
pounds per cubic foot in the U.S. customary system.
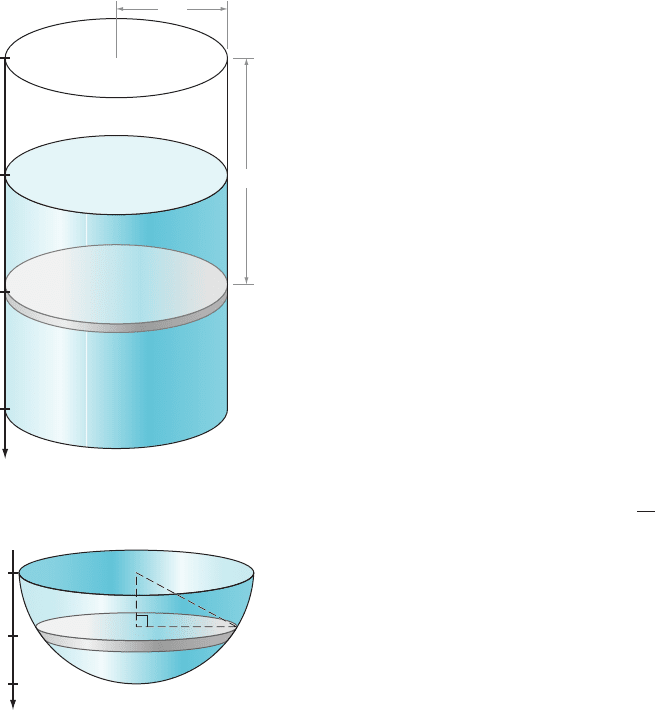
⁄ EX
AMPLE 4 A cylindri cal sump pit is 3 meters deep; its radius is 0.4
meters. Water has accumulated in the pit; the depth of the water is 2 meters. A
sump pump floats on the surface of the water and pumps water to the top of the pit.
How much work is done in pumping out half the water?
Solution In
this type of problem, it is often convenient to orient the positive y-axis
downward, as is indicated in Figure 6. The origin is frequently positioned at the
level to which the fluid must be pumped. Figure 6 also illustrates a thin “slice” of
water y meters below the top of the pit. If the thickness of the slice is Δy meters,
then its volume is π (0.4)
2
Δy m
3
, and its weight is π(0.4)
2
Δy m
3
3 9806.65 N m
23
5
1569.06 πΔy N. The work done to pump this slice y meters to the top is therefore
about 1569.06 π Δy J by equation (7.5.1). The reason this expression is not exact is
that the volume pumped does have some thickness; consequently, not all points are
exactly y meters from the top. To approximate the total work done in pumping out
half the pit, we form the sum
P
1569:06 π y Δy of the contributions of the slices
from y 5 1toy 5 2. Our approximation improves as Δy tends to 0, and in passing to
the limit, we obtain
W 5
Z
2
1
1569:06 π ydy5 1569:06 π
y
2
2
y52
y51
5 2353:59 π N 7394 N: ¥
⁄ EXAMPLE 5 A tank full of water is in the shape of a hemisphere of radius
20
feet. A pump floats on the surface of the water and pumps the water from the
surface to the top of the tank, where the water just runs off. How much work is
done in emptying the tank?
Solution The
tank is sketched in Figure 7. As in the preceding example, we have
positioned a downward- oriented vertical axis that has the origin at the top of the
reservoir. Consider a thin horizontal “slice” at depth y. By solving for the base of
the right triangle indicated in Figure 7, we find that the cross-section of the slice is a
circle of radius
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20
2
2 y
2
q
. If the thickness of the slice is Δy, then the volume of the
slice is π
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
20
2
2 y
2
q
2
Δy cubic feet. It follows that the weight of the slice is
62.428 π(20
2
2 y
2
) Δy pounds, and the work done in raising this slice to the surface
is about 62:428 π ð20
2
2 y
2
ÞΔy y foot-pounds. Passing to an integral as in the
preceding example, we see that the total work is
y
0.4
y
0
1
2
3
m Figure 6
0
y
20
y
20
m Figure 7
584 Chapter
7 Applications of the Integral
