Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.

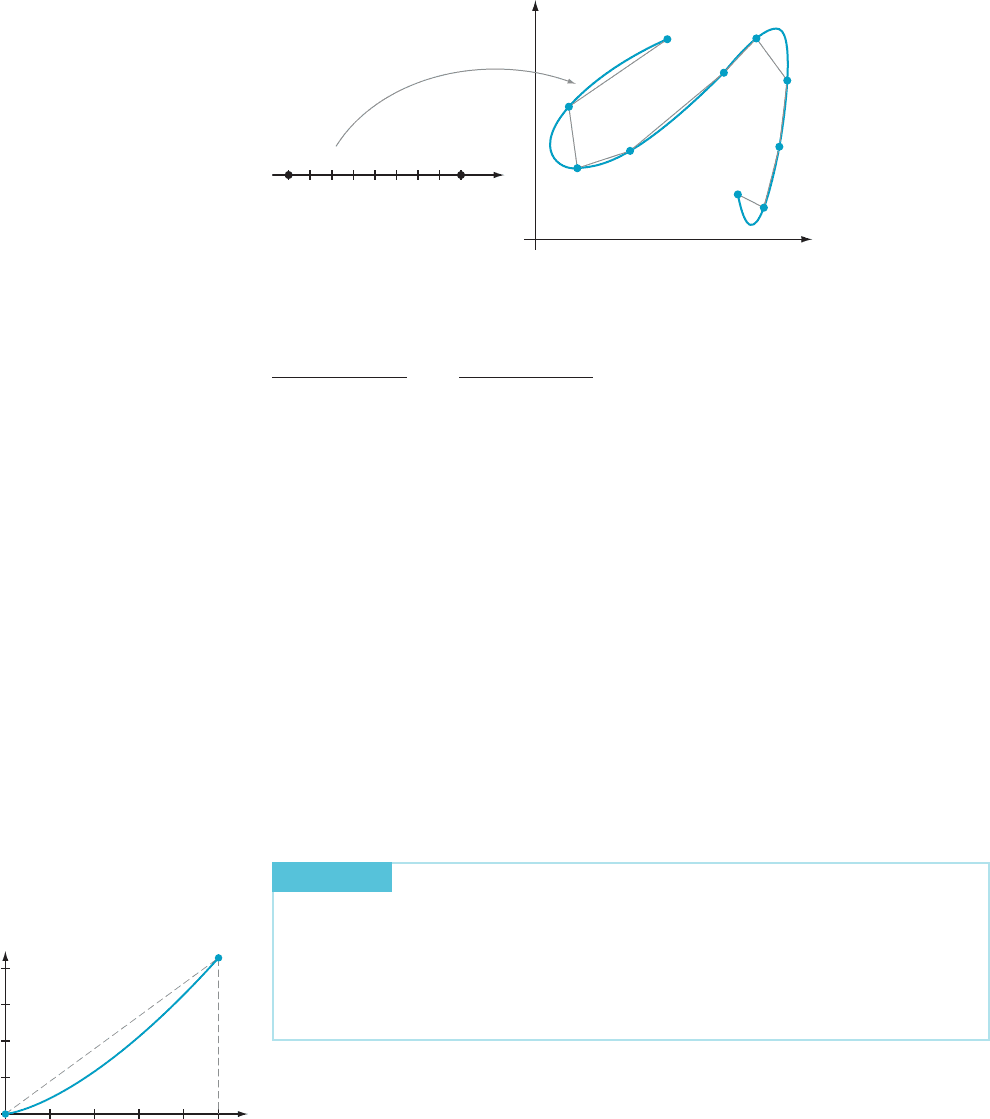
Denoting the midpoint of [t
j21
, t
j
]bys
j
, we observe that
ϕ
1
ðt
j
Þ2 ϕ
1
ðt
j21
Þ
Δt
and
ϕ
2
ðt
j
Þ2 ϕ
2
ðt
j21
Þ
Δt
are the central differenc e quotient approx-
imations of ϕ
1
0
ðs
j
Þand ϕ
2
0
ðs
j
Þ, respectively. Thus
‘
j
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðs
j
Þ
2
1
ϕ
2
0
ðs
j
Þ
2
q
Δt:
We sum the lengths ‘
j
to obtain an approximate length for the curve:
L
X
N
j51
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðs
j
Þ
2
1
ϕ
2
0
ðs
j
Þ
2
q
Δt:
As N increases to infinity and Δt tends to 0, these approximating sums tend to our
intuitive concept of the arc length L of C:
L 5 lim
N-N
X
N
j51
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðs
j
Þ
2
1
ϕ
2
0
ðs
j
Þ
2
q
Δt:
Because the sums on the right side of this formula are Riemann sums for the
integral
R
β
α
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðtÞ
2
1
ϕ
2
0
ðtÞ
2
q
dt, we are led to the follo wing definition.
DEFINITION
If ϕ
1
and ϕ
2
have continuous derivatives on an interval that
contains I 5 [α, β], then the arc length L of the parametric curve
C 5 fðϕ
1
ðtÞ; ϕ
2
ðtÞÞ : α # t # βg is given by
L 5
Z
β
α
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðtÞ
2
1
ϕ
2
0
ðtÞ
2
q
dt: ð7:2:5Þ
⁄ EX
AMPLE 4 Calculate the length L of the param etric curve
C 5 fðϕ
1
ðtÞ; ϕ
2
ðtÞÞ : 0 # t # 4g where ϕ
1
(t) 5 3t
2
and ϕ
2
(t) 5 2t
3
/3.
Solution The
graph of C in Figure 5 leads us to expect a value for L that does not
greatly exceed the straight line distance,
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
48
2
1 ð128=3Þ
2
q
, or 64.22 . . . , between
P
N
C
y
x
x w
1
(t), y w
2
(t)
t
0
t
1
t
2
t
3
t
4
t
N1
t
N
ab
P
N1
P
N2
P
4
P
3
P
2
P
0
P
1
m Figure 4
y
x
x 3t
2
, y 2t
3
/3
40
30
20
10
0
020304048
128/3
64.22
C
(48, 128/3)
m Figure 5
7.2 Arc Length and Surface Area 555
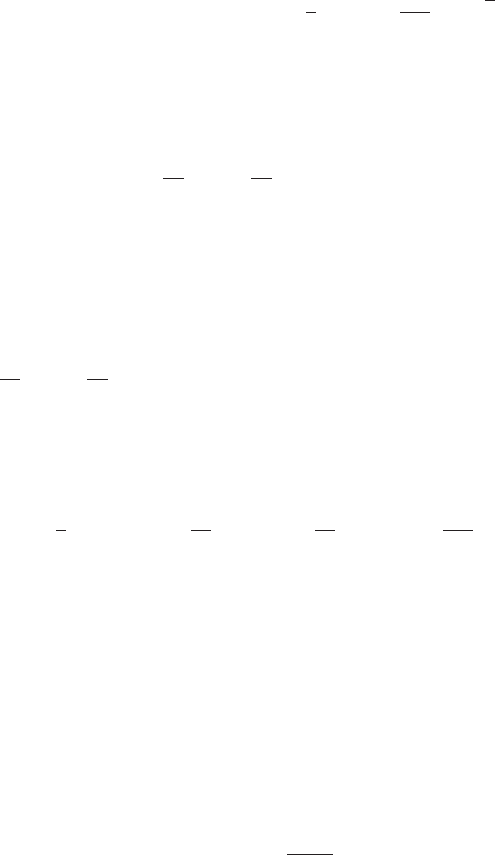
the endpoints (0, 0) and (48, 128/3) of C. For an exact evaluation of L using formula
(7.2.5), we first calculate ϕ
1
0
ðtÞ5 6t and ϕ
2
0
ðtÞ5 2t
2
. It follows that
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðtÞ
2
1
ϕ
2
0
ðtÞ
2
q
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð6tÞ
2
1 ð2t
2
Þ
2
q
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
36t
2
1 4t
4
p
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4t
2
ð9 1 t
2
Þ
q
5 2t
ffiffiffiffiffiffiffiffiffiffiffiffi
9 1 t
2
p
:
Making the substitution u 5 9 1 t
2
, du 5 2tdt and noting that u 5 9andu 5 25 are
the limits of integrat ion corresponding to x 5 0 and x 5 4, we have
L 5
Z
4
0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ϕ
1
0
ðtÞ
2
1
ϕ
2
0
ðtÞ
2
q
dt 5
Z
4
0
2t
ffiffiffiffiffiffiffiffiffiffiffiffi
9 1 t
2
p
dt 5
Z
25
9
u
1=2
du 5
2
3
u
3=2
25
9
5
196
3
5 65:
3 : ¥
In practice, we often do not give names such as ϕ
1
and ϕ
2
to the functions that
define x and y parametrically. When we dispense with the extra notation, formula
(7.2.5) takes the simpler form
L 5
Z
β
α
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
dt
2
1
dy
dt
2
s
dt: ð7:2:6Þ
⁄ EX
AMPLE 5 Calculate the length L of the parametric curve C defined by
the parametric equations x 5 1 1 2t
3/2
and y 5 3 1 2t for 0 # t # 5.
Solution We
begin by calculating
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
dt
2
1
dy
dt
2
s
5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð3t
1=2
Þ
2
1 ð2Þ
2
q
5 ð9t 1 4Þ
1=2
:
Using equation (7.2.6) with the substitution u 5 9t 1 4, du 5 9dt and noting that
u 5 4andu 5 49 are the limits of integration corresponding to x 5 0 and x 5 5,
we have
L 5
Z
5
0
ð9t 1 4Þ
1=2
dt 5
1
9
Z
49
4
u
1=2
dt 5
2
27
u
3=2
u549
u54
5
2
27
ð343 2 8Þ5
670
27
: ¥
Surface Area Let f be a nonnegative function with continuous derivative on the interval [a, b].
Imagine rotating the graph of f about the x-axis. This procedure will generate a
surface of revolution, as shown in Figure 6. We will develop a procedure for
determining the area of such a surface. As with previously developed methods that
have led to integral formulas, we first divide the geometric object into a number of
pieces that can be approximated by a simple shape. The basic shape that we will use
here, a frustum, can be seen in Figure 7. It results when a conical surface is cut by
two planes that are perpendicular to the axis of symmetry. The formula for the
surface area S of a frustum is
Surface Area of frustum 5 2π
r 1 R
2
s ð7:2:7Þ
where r and R are the radii of the circular edges and s is the slant height,as
indicated in Figure 7. Notice that this is the surface area of a cylinder with height
equal to the slant height of the frustum and radius equal to the average radius of
556 Chapter 7 Applications of the Integral
the cross-sections of the frustum. Formula (7.2.7) is elementary in the sense that its
derivation (as outlined in Exercise 62) does not require calculus.
For each positive integer N, we form a uniform partition
a 5 x
0
, x
1
, x
2
, :::, x
N21
, x
N
5 b
of the interval [a, b]. Let Δx denote the common length of the N subintervals.
When the arc of the curve that lies over the j
th
subinterval is rotated about the x-
axis, we obtain a surface that we can approximate by a frustum (as in Figure 8). The
slant height of this frustum can be approximated by the arc length ‘
j
of the graph of
f from (x
j21
, f (x
j21
)) to (x
j
, f (x
j
)). In the discussion of arc length earlier in this
section, we reasoned that there is a point s
j
in the j
th
subinterval such that
‘
j
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðs
j
Þ
2
q
Δx:
We may use the value f (s
j
) at this interior point s
j
to approxi mate the average value
( f (x
j21
) 1 f (x
j
))/2 of f at the endpoints. It follows from formula (7.2.7) that the area
contribution of the j
th
increment of our surface is about
2π f ðs
j
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðs
j
Þ
2
q
Δx:
If we sum up the area contribution from each subinterval of the partition, we find
that the area of our surface of revolution is about
X
N
j51
2π f ðs
j
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðs
j
Þ
2
q
Δx:
The accuracy of this approximation is improved by increasing the number N of
subintervals. As N increases to infinity and Δx tends to 0, these approximating
sums tend to what we think of as surface area S of the surface of revolution:
S 5 lim
N-N
X
N
j51
2π f ðs
j
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðs
j
Þ
2
q
Δx:
But these sums are also Riemann sums for the integral
2π
Z
b
a
f ðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðxÞ
2
q
dx:
These observations lead us to the definition of the surface area of a surface of
revolution:
x
b
y f(x)
x
a
m Figure 6 The graph of a function and the surface it generates
when rotated about the x-axis.
R
s
r
m Figure 7 Surface area of frustum 5
2π
r 1 R
2
S
x
m Figure 8 Slice of surface
approximated by a frustum of
a cone.
7.2 Arc Length and Surface Area 557

DEFINITION
If f is a nonnegative function which has a continuous derivative
on an interval containing [a, b], then the surface area of the surface of revolution
obtained when the graph of f over [a, b] is rotated about the x-axis is given by
2π
Z
b
a
f ðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðxÞ
2
q
dx: ð7:2:8Þ
⁄ EX
AMPLE 6 Let f (x) 5 x
3
for 1 # x # 2. Calculate the area S of the surface
that is obtained by rotating the graph of f about the x-axis.
Solution We
have
S 5 2π
Z
2
1
f ðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðxÞ
2
q
dx 5 2π
Z
2
1
x
3
1 1 ð3x
2
Þ
2
1=2
dx 5
π
27
Z
2
1
3
2
ð1 1 9x
4
Þ
1=2
ð36x
3
Þdx:
We calculate this integral by making the substitution u 5 9x
4
, du 5 36x
3
dx. With
this substitution, the limits of integration for u become 9 and 144. Therefore
S 5
π
27
Z
144
9
3
2
ð1 1 uÞ
1=2
du 5
π
27
ð1 1 uÞ
3=2
144
9
5
π
27
ð145
3=2
2 10
3=2
Þ: ¥
⁄ EXAMPLE 7 Show that S 5 4πr
2
is the surface area of a sphere of radius r.
Solution It
is convenient to think of the sphere as the surface of revolution
generated by rotating the graph of the function f ðxÞ5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
2 x
2
p
; 2r # x # r about
the x-axis. Then
1 1 f
0
ðxÞ
2
5 1 1
2x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
2 x
2
p
2
5 1 1
x
2
r
2
2 x
2
5
ðr
2
2 x
2
Þ1 x
2
r
2
2 x
2
5
r
2
r
2
2 x
2
:
It follows that
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðxÞ
2
q
5 r=
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
2 x
2
p
and
S 5 2π
Z
r
2r
f ðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 f
0
ðxÞ
2
q
dx 5 2π
Z
r
2r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
2 x
2
p
r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r
2
2 x
2
p
dx 5 2πr
Z
r
2r
1 dx 5 4πr
2
: ¥
We may also consider the area of a surface obtained by rotating the graph of a
funct
ion about the y-axis. We do so by using y as the independent variable. Here is
an example:
⁄ EX
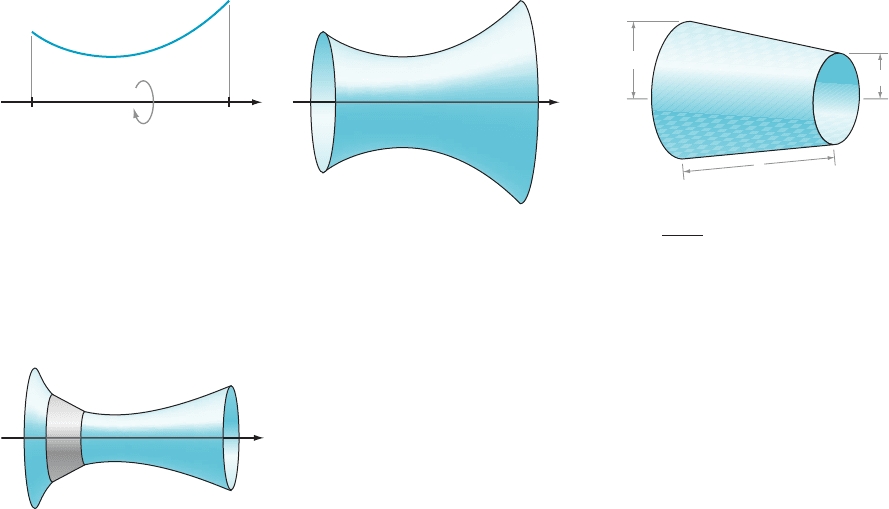
AMPLE 8 Set up, but do not evalua te, the integral for finding the area
of the surface obtained when the graph of f (x) 5 x
4
,1# x # 5, is rotated about the
y-axis.
Solution We
write y 5 x
4
and solve for x, obtaining x 5 y
1/4
. We think of the curve
that is to be rotated as the graph of g( y) 5 y
1/4
,1# y # 625. The surface of rotation
can be seen in Figure 9. The formula for surface area is
2π
Z
625
1
gðyÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 g
0
ðyÞ
2
q
dy:
558 Chapter 7 Applications of the Integral
Calculating g
0
( y) and substituting, we find that the desired surface area is the value
of the integral
2π
Z
625
1
y
1=4
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1
1
4
y
23=4
2
s
dy: ¥
QUICK QUIZ
1. The arc length of the graph of y 5 x
3
between (0, 0) and (2, 8) is equal to
R
2
0
gðxÞdx for what function g(x)?
2. The arc length of the graph of the parametric curve x 5 e
t
, y 5 t
2
between
(1, 0) and (e, 1) is equal to
R
1
0
gðtÞdt for what function g(t)?
3. The graph of y 5 x
3
between (0, 0) and (2, 8) is rotated about the x-axis. The area
of the resulting surface of revolution is 2π
R
2
0
gðxÞdx for what function g(x)?
4. What is the area of the surfa ce of revolution that results from rotating the graph
of y 5 mx,0# x # h about the x-axis?
Answers
1.
ffiffiffiffiffiffiffiffi
ffiffiffiffiffiffiffi
1 1 9x
4
p
2.
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
e
2t
1 4t
2
p
3. x
3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 9x
4
p
4. π mh
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 m
2
p
y
100
54321
200
300
400
500
600
y
f(x) x
4
or
g(y) y
14
x x
m Figure 9 The surface generated by rotating the graph of f about the y-axis. The xy-plane
is tilted to reveal the opening at the bottom of the surface
EXERCISES
Problems for Practice
c In each of Exercises 124, the graph of the given function f
with given domain I is a line segment. Use formula (7.2.3) to
calculate the arc length of the graph of f. Verify that this
length is the distance between the two endpoints. b
1. f (x) 5 3xI5 [1,
4]
2. f (x) 5 2x 1 1 I 5 [0, 4]
3. f (x) 5 3 2 xI5 [21, 2]
4. f (x) 5 10 2 2xI5 [0, 5]
c In each of Exercises 5212, calculate the arc length L of
the
graph of the given function over the given interval. b
5. f (x) 5 2 1 x
3/2
I 5 [1, 4]
6. f (x) 5 (x 2 1)
3/2
I 5 [1, 5]
7. f (x) 5 3 1 (2x 1 1)
3/2
I 5 [0, 4]
8. f (x) 5 (5 2 2x)
3/2
I 5 [1/2, 2]
9. f (x) 5 ln(cos(x)) I 5 [0, π/3]
10. f (x) 5 ln(sin(x)) I 5 [π/4, π/2]
11. f ðxÞ5
2
3
ðx
2
1 1Þ
3=2
I 5 [0, 1]
12. f (x) 5 2(x
2
1 1/3)
3/2
I 5 [1, 3]
c In each of Exercises 13216, calculate the arc length of the
graph
of the given equation. b
13. x 5 y
3/2
2 10# y # 1
14. x 5 ( y 2 8)
3/2
1 28# y # 12
15. x
2
/y
3
5 4 1/3 # y # 7
16. exp(x) 5 cos( y)0# y # π /4
7.2 Arc Length and Surface Area 559
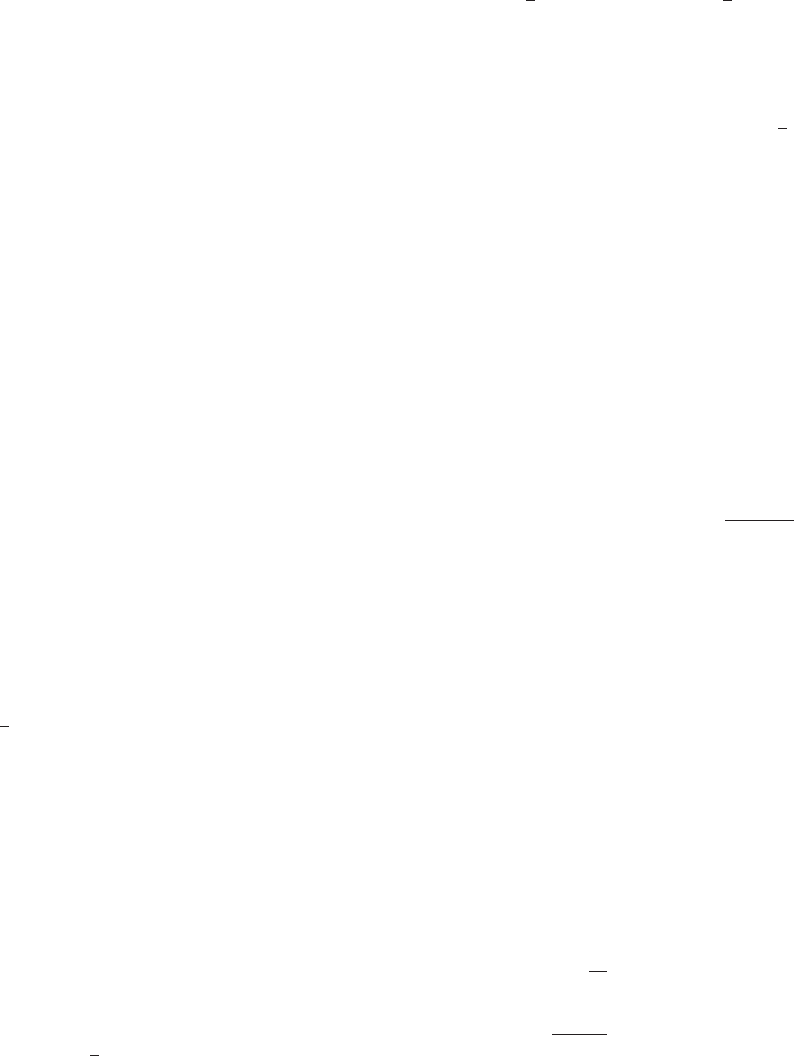
c In each of Exercises 17224, calculate the length of the
given parametric curve. b
17. x 5 3t 2 7 y 5 5 2 4t 21 # t # 1
18. x 5 5t 2 7 y 5 12t 2 # t # 7
19. x 5 4
cos(2t) y 5 4 sin(2 t) 2π/6 # t # π/6
20. x 5 sin(πt
2
) y 5 cos(πt
2
)0# t # 1
21. x 5 3t
2
y 5 2t
3
0 # t # 1
22. x 5 exp(2t) y 5 exp(3t) 21 # t # 1
23. x 5 e
t
cos(t) y 5 e
t
sin(t)0# t # 1
24. x 5 cos
3
(t) y 5 sin
3
(t)0# t # π/2
c In each of Exercises 25230, calculate the area S of
the
surface obtained when the graph of the given function is
rotated about the x-axis. b
25. f (x) 5 3x 2 1
[1, 4]
26. f (x) 5 x
3
/3 [0, 1]
27. f (x) 5 3x
1/2
[7/4, 4]
28. f (x) 5 x
3
/3 1 1/(4x) [1, 2]
29. f (x) 5 e
x
/2 1 e
2x
/2 [21, 1]
30. f (x) 5 (x 1 1)
1/2
[1, 11]
c In each of Exercises 31234, calculate the area S of
the
surface obtained when the given function, over the given
interval, is rotated about the y-axis. b
31. f (x) 5 x/4 2 2
[8, 12]
32. f (x) 5 x
2
[0,
ffiffiffi
2
p
]
33. f (x) 5 x
1/3
[0, 8]
34. f (x) 5 (3x)
1/3
[0, 1/3]
Further Theory and Practice
c In Exercises 35238, calculate the arc length L of the graph
of the given equation. b
35. y 5
1
2
x
2
0 # x # 1.
36. y 5 ln(x)1# x # e.
37. y 5 2
ffiffiffi
x
p
1/3 # x # 1.
38. y 5 lnðx
2
2 1Þ
ffiffiffi
2
p
# x #
ffiffiffi
3
p
.
c In each of Exercises 39244, calculate the arc length of the
graph
of the given function over the given interval. (In these
exercises, the functions have been contrived to permit a
simplification of the radical in the arc length formula.) b
39. f (x) 5 (1/3)(x
2
1 2)
3/2
I 5 [0, 1]
40. f (x) 5 (1/6)x
3
1 (1/2)x
2 1
I 5 [1, 2]
41. f (x) 5 e
x
/2 1 e
2x
/2 1 7 I 5 [0, 1]
42. f (x) 5 (2
x
1 2
2 x
)/(2 ln(2)) I 5 [0, 2]
43. f (x) 5 2x
4
1 1/(64x
2
) I 5 [1/2, 1]
44. f (x) 5
2x
1/2
1
9
4
3=2
I 5 [1/4, 1]
c In each of Exercises 45252, calculate the length L of
the
given parametric curve. b
45. x 5 t cos(t) y 5 t sin(t)0# t # 3π
46. x 5 t
2
cos(t) y 5 t
2
sin(t)0# t #
ffiffiffi
5
p
47. x 5
1
2
t
2
2 ty5
1
2
t
2
1 t 0 # t # 1
48. x 5 cos(t) 1 t sin(t) y 5 sin(t) 2 t cos(t)0# t # 2π
49. x 5 t 2 sin(t) y 5 1 2 cos(t)0# t # 2π
50. x 5 2 arctan(t) y 5 ln(1 1 t
2
)0# t # 1
51. x 5 cos(t) 1 ln(tan(t/2)) y 5 sin(t) π/3 # t # π/2
52. x 5 3 exp(t) y 5 2 exp
3
2
t
0 # t # 1
53. Find the arc length of the graph of y
4
2 16x 1 8/y
2
5 0
between P 5 (9/8, 2) and Q 5 (9/16,1).
54. Find the arc length of the graph of 30yx
3
2 x
8
5 15
between P 5 (0.1, 500.0 ...) and Q 5 (1, 8/15).
55. Suppose that f is a function with a continuous derivative
on an open interval containing [a, b]. Let C be the graph of
f over the interval [a, b], and let C
0
be the curve with
endpoints (a 1 h, f (a) 1 v) and (b 1 h, f (b) 1 v), is
obtained by translating C horizontally by an amount h and
vertically by an amount v. Prove that the lengths of C and
C
0
are equal.
56. Suppose that a . b . 0. Let ε 5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
2
2 b
2
p
=a. Show that,
for any 0 , ξ , a, the length L(ξ) of the arc of the ellipse
x
2
/a
2
1 y
2
/b
2
5 1 that lies above the interval [0, ξ] of the
x-axis integral is given by
Lðξ Þ5
Z
ξ
0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
2
2 ε
2
x
2
a
2
2 x
2
r
dx:
Make a change of variable to write L(ξ) in terms of the
elliptic integral
Eðε; ηÞ5
Z
η
0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 ε
2
sin
2
ðtÞ
q
dt:
Although elliptic integrals cannot be evaluated using
elementary functions, they are built into computer alge-
bra systems, and their values have been tabulated.
57. Suppose that a . b . 0. Let ε 5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
2
2 b
2
p
=a, as in the
preceding exercise. Parameterize the ellipse x
2
/a
2
1 y
2
/
b
2
5 1 by the equations x 5 a sin(t), y 5 b cos(t),
(0 # t # 2π). Let L(τ) denote the arc length of that part of
the ellipse that is given by 0 # t # τ # π/2. Express L(τ)in
terms of the function E(ε, η) of the preceding exercise.
c In each of Exercises 58261, calculate the area S of
the
surface obtained when the graph of the given function is
rotated about the x-axis. b
58. f ðxÞ5 expðxÞ 0 # x # 1.
59. f ðxÞ5 x
4
1
1
32
x
22
1=2 # x # 1
60. f ðxÞ5 sinðxÞ 0 # x # π=2
61. f ðxÞ5
3x
4
1 1
6x
1 # x # 2
62. When the right circular cone of slant height ‘ and base radius
R is cut alonga lateral edge andflattened, it becomes a sector
of a circle of radius ‘ and central angle θ, as in Figure 10.
Prove that θ 5 2πR/‘. Use this observation to derive formula
(7.2.7) for the surface area of a frustum of a cone.
560 Chapter 7 Applications of the Integral
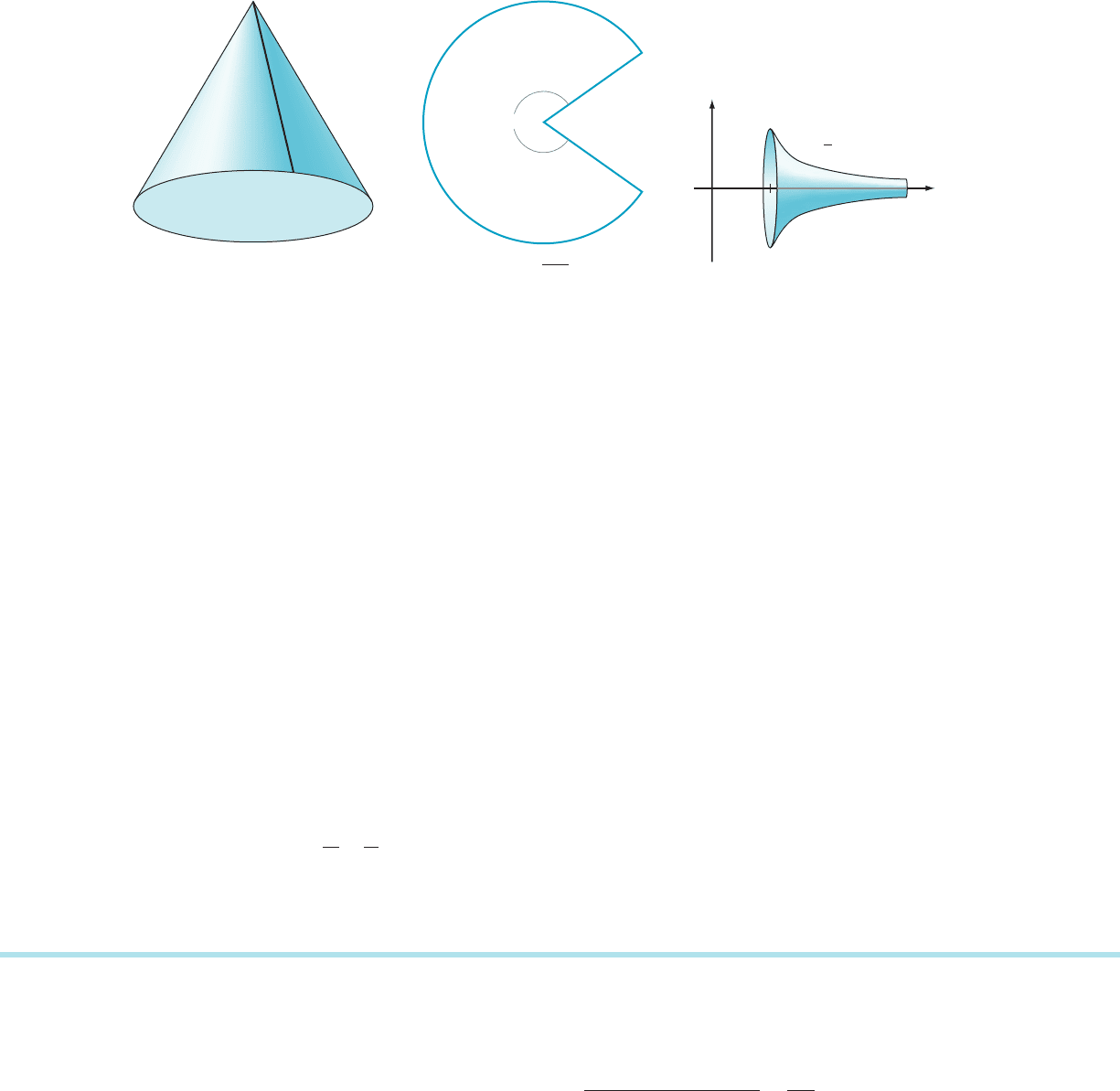
Base radius R
2R
ᐉ
ᐉ
ᐉ
m Figure 10
x
y
y
1
x
1
m Figure 11 A section of Torricelli’s infinitely
long solid
63. By means of integration, calculate the surface area of a
right circular cone of radius R and height h. (The formula
you derive can, of course, be obtained directly from for-
mula (7.2.7) with r 5 0.)
64. Let C be the curve parameterized by x 5 ϕ
1
ðtÞ; y 5 ϕ
2
ðtÞ;
α # t # β. Suppose that 0 , ϕ
1
0
(t)forallt,andseta 5 ϕ
1
(α)
and b 5 ϕ
1
(β). Then, C is the graph of y 5 ðϕ
2
ϕ
21
1
ÞðxÞ;
a # x # b. Show that formula (7.2.5) for the length of C can
be obtained from formula (7.2.3) with f 5 ϕ
2
ϕ
21
1
.
65. Torricelli’s infinitely long solid T is the solid of revolution
obtained by rotating about the x-axis the first quadrant
region that is bounded above by the graph of y 5 1/x,
below by the x-axis, and on the left by x 5 1 (see Figure
11). Let V
N
and S
N
denote the volume and surface area of
that part of Torricelli’s solid for which 1 # x # N. Calcu-
late the finite number V 5 lim
N-N
V
N
. Show that ln(N) ,
S
N
, and therefore lim
N-N
S
N
5 N. Thus Torricelli’s solid
has finite volume, but its surface area is infinite.
Calculator/Computer Exercises
66. Use Simpson’s Rule to calculate the arc length L of the
ellipse
x
2
16
1
y
2
4
5 1
to 2 decimal places of accuracy.
67. Use Simpson’s Rule to calculate the arc length of the
graph of y 5 sin(x), 0 # x # 2π, to four decimal places of
accuracy.
68. Plot T(x) 5 4x
3
2 3x for 21 # x # 1. Notice that the plot is
contained in the square [21, 1] 3 [21, 1]. Of all degree 3
polynomials that have this containment property, T has
the longest arc length. Use Simpson’s Rule to calculate
the arc length of the graph of y 5 T(x), 21 # x # 1 to four
decimal places of accuracy.
69. The surface of a flashlight reflector is obtained when
y 5 2:05
ffiffiffi
x
p
1 0:496; 0:02 # x # 2:80 cm is rotated about
the x-axis. Calculate its surface area to two significant
digits.
70. The equation of the St. Louis Gateway Arch is
y 5 693:8597 2 34:38365 ðe
kx
1 e
2kx
Þ
for k 5 0.0100333 and 2 299.2239 , x , 299.2239. Find an
equation of a parabola with the same vertex and x-
intercepts. Plot both curves on the same set of coordinate
axes. Compute the length of each.
71. Calculate to four significant digits the surface area that
results when the graph of the Gateway Arch equation
(given in the preceding exercise) is rotated about the
y-axis.
7.3 The Average Value of a Function
If we took five temperature readings during the day that were 50, 58, 68, 70, an d
54 (in degrees Fahrenheit), then the average value of our readings would be
50 1 58 1 68 1 70 1 54
5
5
300
5
5 60:
7.3 The Average Value of a Function 561
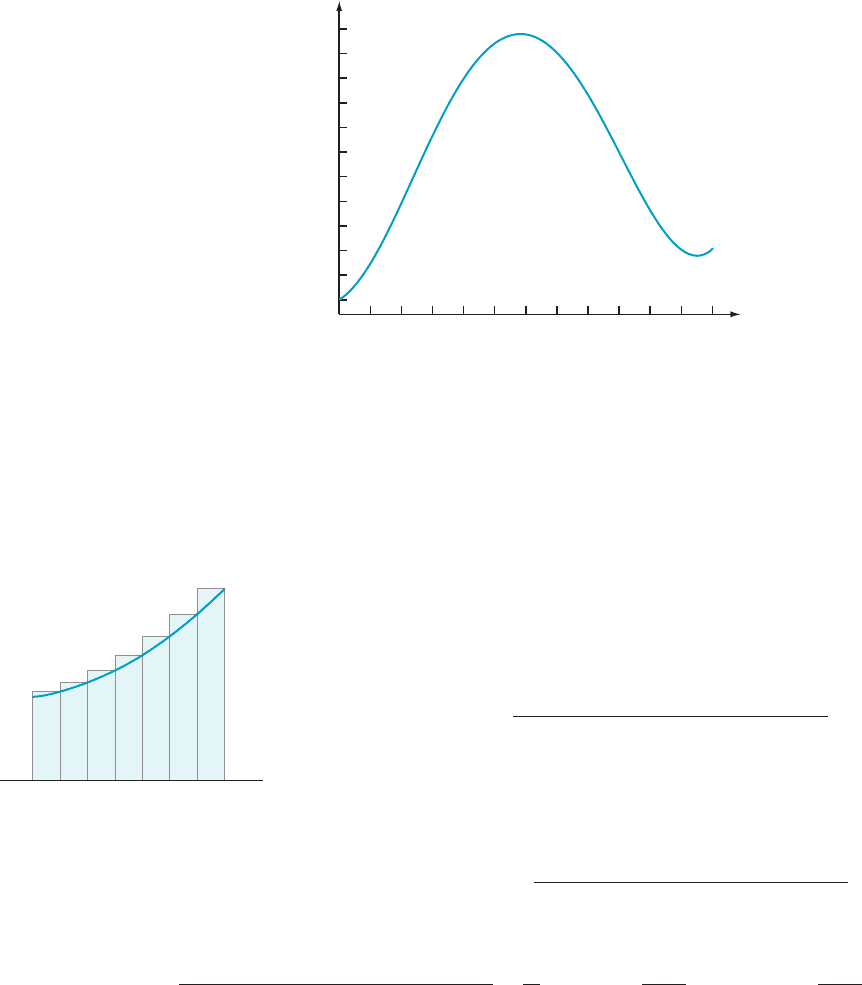
Frequently we need to average infinitely many values. For instance, consider the
plot of temperature that is given in Figure 1. To speak of an average temperatur e
during the day, we must average the temperature at infinitely many inst ants of
time. The meth od for averaging infinitely many values is to use an integral, which is
the subject of this section.
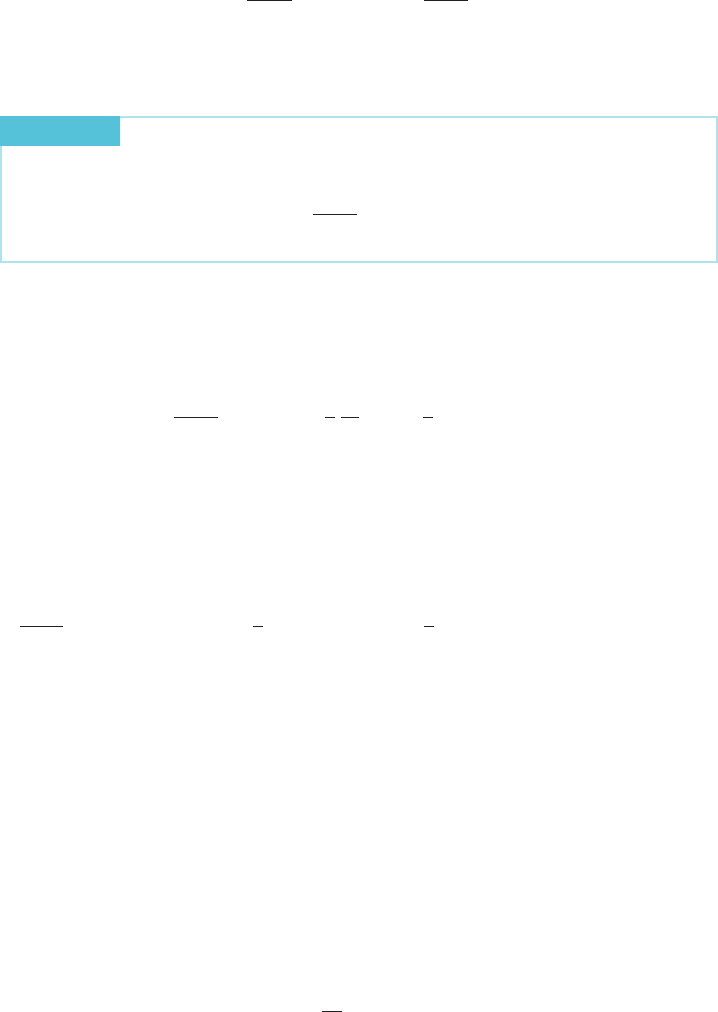
The Basic Technique Suppose that f is a continuous function whose domain contains the interval [a, b].
To estimate the average value of f on this interval, we take a uniform partition of
the interval:
a 5 x
0
, x
1
, x
2
, :::, x
N21
, x
N
5 b:
As usual, let Δx 5 (b 2 a)/N denote the common length of the subintervals that are
formed by the partition. If we add up the values of f at the right endpoints of the
partition (Figure 2) and divid e by the number of points, then the resulting
expression is an approximation to the average value f
avg
of f :
f
avg
f ðx
1
Þ1 f ðx
2
Þ1 1 f ðx
N21
Þ1 f ðx
N
Þ
N
:
As we let N increase to infinity, our approximation uses more and more points from
the interval [a, b] and becomes more accurate. We therefore define the average
value f
avg
of f (x) for x in [a, b]tobe
f
avg
5 lim
N-N
f ðx
1
Þ1 f ðx
2
Þ1 1 f ðx
N21
Þ1 f ðx
N
Þ
N
:
We may rewrite this expression as
f ðx
1
Þ1 f ðx
2
Þ1 1 f ðx
N21
Þ1 f ðx
N
Þ
N
5
1
N
X
N
j51
f ðx
j
Þ5
1
NΔx
X
N
j51
f ðx
j
ÞΔx 5
1
b 2 a
X
N
j51
f ðx
j
ÞΔx:
72
50
24681012
Time
(
hours
)
14 16 18 20 22 24
52
54
56
58
60
62
Temperature (degrees Fahrenheit)
64
66
68
70
m Figure 1
x
1
x
N1
x
N
bx
2
x
3
a x
0
f
m Figure 2
562 Chapter
7 Applications of the Integral
Because
P
N
j51
f ðx
j
ÞΔx is a Riemann sum for the integral
R
b
a
f ðxÞdx, we conclude
that
f
avg
5 lim
N-N
1
b 2 a
X
N
j51
f ðx
j
ÞΔx 5
1
b 2 a
Z
b
a
f ðxÞdx:
We summarize the resul t of our calculation in the following definition.
DEFINITION
Suppose that f is a Riemann integrable function on the interval
[a, b]. The averag e value of f on the interval [a, b] is the number
f
avg
5
1
b 2 a
Z
b
a
f ðxÞdx: ð7:3:1Þ
⁄ EX
AMPLE 1 What is the average value f
avg
of the function f (x) 5 x
2
on the
interval [3, 6]?
Solution The
average is
f
avg
5
1
6 2 3
Z
6
3
x
2
dx 5
1
3
x
3
3
x56
x53
5
1
9
ð6
3
2 3
3
Þ5 21: ¥
⁄ EXAMPLE 2 A rod of length 9 cm has temperature distribution
TðxÞ5 ð 2 x 2 6x
1=2
Þ
C for 0 # x # 9. This means that, at position x on the rod, the
temperature is (2x 2 6x
1/2
)
C. Calculate the average temperature of the rod.
Solution The
computation
T
avg
5
1
9 2 0
Z
9
0
ð2x 2 6x
1=2
Þdx 5
1
9
ðx
2
2 4x
3=2
Þ
x59
x50
5
1
9
ð81 2 4 27Þ2 ð0 2 4 0Þ
523
shows that the average temperature of the rod is 3
C below zero. ¥
⁄ EXAMPLE 3 Suppose that, at a weather station, the temperature f in
degrees Fahrenheit at the time x is recorded to be
f ðxÞ5 0:00103265x
4
2 0:04678932x
3
1 0:50831530 x
2
1 0:64927850x 1 50
for 0 # x # 24 hours. What is the average temperature for that day?
Solution The
graph of f was given in Figure 1. By scanning the values taken by f,
we might estimate the average value to be between 60 and 64. At the beginning of
this section, we used the five values f (0) 5 50, f (4) 5 58, f (8) 5 68, f (14) 5 70, and
f (22) 5 54, to obtain a sample average of 60. Now we can calculate the average
over all values of f :
f
avg
5
1
24
Z
24
0
f ðxÞdx:
Using a computer algebra system to evaluate the integral (or a calculator to per-
form the arithmetic calculations that arise when the integral is evaluated by means
7.3 The Average Value of a Function 563

of the Fundamental Theorem of Calculus), we obtain f
avg
5 62.21 (to two decimal
places).
¥
INSIGHT
The expected cost of heating a building during the winter is often calcu-
lated using the concept of “degree days.” A simple definition of degree day for a given
day is 65 degrees Fahrenheit less the average outdoor temperature for that day. For
example, if the cost of heating the weather station of Example 3 is $0.35 per degree day,
then we would expect the heating bill for the day in question to be about $0.35
(65 2 62.205687) $0.98.
⁄ EXAMPLE 4 Let f
avg
denote the average value of f over the interval [a, b].
Show that the function f and the constant function g(x) 5 f
avg
have the same
integral over [a, b].
Solution We
obtain the required equality as follows:
Z
b
a
gðxÞdx 5
Z
b
a
f
avg
dx 5 ðb 2 aÞf
avg
5 ðb 2 aÞ
1
ðb 2 aÞ
Z
b
a
f ðxÞdx
5
Z
b
a
f ðxÞdx: ¥
INSIGHT
This result is the continuous analogue of a well-known fact about discrete
averages. Namely, if
y is the average value of the N numbers y
1
; y
2
;:::;y
N
, then
X
N
j51
y 5 N y 5 N
1
N
X
N
j51
y
j
5
X
N
j51
y
j
:
It is often the case that a theorem about finite sums has a continuous analogue in which
the sums are replaced by integrals.
b A LOOK BACK In Section 5.3 of Chapter 5, you learned the Mean Value Theorem
for Integrals. That theorem asserted that, if f is continuous on an interval [a, b],
then there is a value c in the interval such that
f ðcÞ5
1
b 2 a
Z
b
a
f ðxÞdx: ð7:3 :2Þ
Because the right side of equation (7.3.2) is f
avg
, we may interpret the Mean Value
Theorem for Integrals in this way: A continuous function on a closed bounded
interval assumes its average value. This is a property that discrete samples do not
necessarily have. The average of the five temperatures of Example 3 is 60, which
does not equal any of the five sample temperatures.
⁄ EX
AMPLE 5 At what point (or points) is the temperature of the metal rod
of Example 2 equal to the average temperature of the rod?
Solution Because
the temperature of the rod, 2x 2 6x
1/2
, is continuous, we can be
sure that there is at least one point at which the temperature is equal to the average
temperature 23
C (a value that was calculated in Example 2). Figure 3 shows that
there are actually two points at which the average temperature is attained. To find
1
2
3
4
2468
y 3
3
2
3
3
y 2x 6x
12
3
2
3
3
x
y
m Figure 3
564 Chapter
7 Applications of the Integral
