Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

INSIGHT

It is important that the limits on the right side of equation (6.7.1) be

calculated independently. In particular, taking M 52N and calculating one limit is an

incorrect shortcut. In the case of Example 5, we have

1 1 x

dx 5 0 for every N.It

follows that lim

N-N

1 1 x

dx 5 0 As Example 5 shows, the improper integral

1 1 x

dx is divergent. It does not have 0 or any other number as its value.

⁄ EXAMPLE 6 Evaluate the improper integral

1 1 x

dx:

Solution To

evaluate this integral, we must break up the interval (2N,N) into two

pieces. The subintervals (2N, 0] and [0,N) are a natural choice, but the selection of

0 as a place to break the interval is not important: Any other point would do in this

example. Next, we evaluate separately the improper integrals

1 1 x

dx and

1 1 x

dx that result from our choice. For the ﬁrst of these two improper

integrals, we have

1 1 x

dx 5 lim

N-N

1 1 x

dx 5 lim

N-N

arctanðxÞ



5 lim

N-N



arctanðNÞ2 0



The second integral evaluates to π/2 in a similar manner. Because each of the

integrals on the half line is convergent, we conclude that the original improper

integral over the entire real line is convergent and that its value is

π/2 1 π/2, or π.

Proving Convergence

Without Evaluation

In the preceding section, you learned a comparison theorem for unbounded inte-

grands. Similar theorems pertain to integrals over inﬁnite intervals. We state such a

theorem for the interval [a,N). Analogous results hold for improper integrals over

(2N, b] and (2N,N).

THEOREM 1

(Comparison Theorem for Integrals over Unbounded Intervals)

Suppose that f and g are continuous functions on the interval [a,N) and that

0 # f (x) # g (x) for all a , x.

a. If

gðxÞdx is convergent, then

f ðxÞdx is also convergent and

f ðxÞdx #

gðxÞdx:

b. If

f ðxÞdx is divergent, then

gðxÞdx is also divergent.

Notice that the Comparison Theorem does not say anything about

f ðxÞdx if

gðxÞdx is convergent and g is less than f. To use the Comparison Theorem to

show that an improper integral

f ðxÞdx is convergent , we must ﬁnd a function g

that is greater than or equal to f and for which

gðxÞdx is convergent. If A and p are

positive constants with p . 1, then g(x) 5 A/x

is often a useful comparison function

for proving convergence on an interval of the form [a,N). Refer to Example 3.

6.7 Improper Integrals—Unbounded Intervals 525

⁄ EXAMPLE 7 Show that

dx is convergent.

Solution We

will compare f ðxÞ5 e

to g(x) 5 e

on the interval [1,N). Notice that

x # x

for 1 # x.Therefore2x

#2x and e

# e

for 1 # x. Next, we calculate

lim

N-N

gðxÞdx 5 lim

N-N

dx 5 lim

N-N







2 lim

N-N





From this calculation, we conclude that

gðxÞdx is convergent. From the

Comparison Theorem, we conclude that

f ðxÞdx is also convergent. In other

words, lim

N-N

dx exists and is ﬁnite. It follows that

lim

N-N

dx 5 lim

N-N



dx 1



dx 1 lim

N-N

exists and is ﬁnite, which establishes that

dx is convergent.

INSIGHT

The Comparison Theorem can be very useful for approximating a

convergent improper integral that cannot be evaluated exactly. (See Exercises 8184.)

As it happens, there are several advanced techniques that yield the exact value of the

improper integral in Example 7. The resulting formula,

dx 5

ﬃﬃﬃ

; ð6:7:2Þ

has fundamental importance in probability and statistics.

QUICK QUIZ

1. Calcul ate

dx:

2. Calcul ate

1 1 x

dx:

3. True or false: If f is continuous on (0,N), unbounded at 0, and if c . 0, then

f ðxÞdx is convergent if and only if both improper integrals

f ðxÞdx and

f ðxÞdx are convergent.

4. Use the Comparison Theorem to determine which of the following improper

integrals converge:

sinð1=xÞ

dx; b.

2 1 sinðxÞ

dx; c.

1 1 x

dx;

expð2x

1 1 x

dx:

Answers

1. 1 2. 3π/4

3. True 4. (a) and (d)

EXERCISES

Problems for Practice

c In each of Exercises 1220, determine whether the given

improper integral converges or diverges. If it converges, then

evaluate it. b

23=2

ﬃﬃﬃ

ð3 1 xÞ

3=2

526 Chapter 6 Techniques of Integration

1 1 x

ð1 1 x

2x=2

xðx 2 1Þ

10.

1 1

11.

ðe

1 1Þ

12.

1 5x 1 6

13.

1 8

ðx

1 1Þðx

1 2Þ

14.



x 1 1

1 1



15.

23x

16.

22x

17.

xlnðxÞ

18.

xln

ðxÞ

19.

arctanðxÞ

1 1 x

20.

ð2=3Þ

c In each of Exercises 21236, determine whether the given

improper

integral converges or diverges. If it converges, then

evaluate it. b

21.

22.

21=3

23.

ð1 1 xÞ

4=3

24.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

3 2 x

25.

ð3 2 xÞ

3=2

26.

ð1 1 x

27.

ð1 1 x

3=2

28.

ð1 1 x

29.

x=3

30.

xexpð2x

Þdx

31.

xexpðx=2Þdx

32.

33.

sinðπ=xÞ

34.

lnð3Þ=2

1 1

35.

ð2 2 xÞln

ð2 2 xÞ

36.

lnð2 2 xÞ

2 2 x

c In each of Exercises 37244, determine whether the given

improper

integral converges or diverges. If it converges, then

evaluate it. b

37.

38.

39.

4 1 x

40.

1 1 x

41.

ð1 1 x

42.

1 2x 1 10

43.

1 3x

1 2

44.

x 1 2

ðx

1 1Þ

c In each of Exercises 45248, an income stream f (t)

is given

(in dollars per year with t 5 0 corresponding to the present).

The income will commence T

years in the future and con-

tinue in perpetuity. Calculate the present value of the income

stream assuming that the discount rate is 5%. b

45. f(t) 5 1000; T

5 0

46. f(t) 5 1000; T

5 20

47. f(t) 5 1000 1 50t; T

5 0

48. f(t) 5 1000 1 50t; T

5 20

Further Theory and Practice

c In each of Exercises 49254, determine whether the given

improper integral converges or diverges. If it converges, then

evaluate it. b

49.

arctanðxÞdx

50.

lnðxÞdx

51.

52.

x11

6.7 Improper Integrals—Unbounded Intervals 527

53.

cosðxÞdx

54.

1 1

c Each of the improper integrals in Exercises 55260 is

improper

for two reasons. Determine whether the integral

converges or diverges. If it converges, then evaluate it. b

55.

expð21=xÞ

56.

expð2

ﬃﬃﬃ

57.

xln

ðxÞ

58.

xln

1=3

ðxÞ

59.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

60.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 4

61. Show that there is no value of p for which

dx is

convergent.

62. For which values of p is

xln

ðxÞ

dx convergent?

c In each of Exercises 63268, use the Comparison Theorem

establish that the given improper integral is convergent. b

63.

1 1 x

64.

2 1 sinðxÞ

65.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

5=2

66.

1 1 e

67.

ﬃﬃﬃ

68.

1 1

c In each of Exercises 69274, use the Comparison Theorem

establish that the given improper integral is divergent. b

69.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

70.

lnðxÞ

71.

sin

ðxÞ1 x

3=2

72.

3 2 sinðxÞ

2x 2 1

73.

expðxÞ

xexpðxÞ2 1

74.

arctanðxÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

75. Use formula (6.7.2) to evaluate the (doubly) improper

integral

ﬃﬃﬃ

dx:

76. Let μ and σ be real constants with σ . 0. Use formula

(6.7.2) to evaluate

exp



x 2 μ



dx:

77. Let μ and σ be real constants with σ . 0. Use formula

(6.7.2) to evaluate

xexp



x 2 μ



dx:

78. Show that the improper integral ΓðsÞ5

s21

dx is

convergent for s . 0. This function of s is called the

gamma function.

79. The gamma function Γ is deﬁned in the preceding exer-

cise. Integrate by parts to derive the functional equation

Γ(s 1 1) 5 sΓ( s ) for s . 0. By calculating Γ(1) and using

the functional equation for Γ, deduce that Γ(n 1 1) 5 n!

for each natural number n.

80. Suppose that f is a continuous nonnegative function such

that

f ðxÞdx is convergent. At ﬁrst one might expect that

lim

x-N

f ðxÞ5 0, but, in fact, this limit does not have to

hold. For each n 2 Z

let V

5 (n,1), P

5 (n 2 1/2

,0),

and Q

5 (n 1 1/2

, 0). Let O denote the origin. Finally, let

f be the nonnegative continuous function deﬁned on [0,N)

so that its graph consists of the line segments

; P

;

; Q

; P

; V

; Q

;: : : (ad inﬁnitum).

Show that lim

x-N

f ðxÞ does not exist. Show that

f ðxÞdx

is convergent, and calculate its value.

Calculator/Computer Exercises

c In each of Exercises 81284, a continuous function f (x)is

given. Determine a function g (x) 5 cx

such that (a) 0 # f(x)

# g(x) for each x in [1,N), and (b)

gðxÞdx is convergent.

This shows that

f ðxÞdx is convergent by the Comparison

Theorem. By determining a positive ε such that

gðxÞdx , 5 3 10

; approximate

f ðxÞdx to two decimal

places. b

81. f ðxÞ5 1=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

1 1 x

82. f (x) 5 (3 1 sin(x))/x

83. f (x) 5 1/ x

84. f ðxÞ5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 3x

528 Chapter 6 Techniques of Integration

Summary of Key Topics in Chapter 6

Integration by Parts

(Section 6.1)

If u and v are

continuously differentiable functions, then

ðu  vuÞdx 5 uv 2

ðv  uuÞdx:

This formula is often used to treat integrals of products of functions. The inte-

gration by parts formu la can be written concisely as

udv 5 uv 2

vdu:

Powers and Products

of Sines and Cosines

(Section 6.2)

It is possible to evaluate integrals of the form

sin

ðxÞcos

ðxÞdx;

for m and n nonnegative integers by using one of three procedures. If m is odd, then

m 5 2k 1 1 for some nonnegative integer k. We rewrite the integral as

sin

ðxÞcos

ðxÞdx 5



sin

ðxÞ



cos

ðxÞsinðxÞdx 5



1 2 cos

ðxÞ



cos

ðxÞsinðxÞdx:

The substitution u 5 cos(x), du 52sin(x) dx can be applied to this last integral. If

n 5 2‘ 1 1 is odd, we proceed in a similar manner. We write

sin

ðxÞcos

ðxÞdx 5



cos

ðxÞ



‘

sin

ðxÞcosðxÞdx 5



1 2 sin

ðxÞ



‘

sin

ðxÞcosðxÞdx

and make the substitution u 5 sin(x), du 5 cos(x) dx. If both powers m 5 2k and

n 5 2‘ are even with ‘ # k, we write the integral as

sin

ðxÞcos

2‘

ðxÞdx 5

sin

ðxÞ



1 2 sin

ðxÞ



‘

dx;

expand the integrand, and integrate the resulting terms using the reduction formula

sin

ðxÞdx 52

sinðxÞ

n21

cosðxÞ1

n 2 1

sinðxÞ

n22

dx:

If k , ‘, we write the integral as

sin

ðxÞcos

2‘

ðxÞdx 5



1 2 cos

ðxÞ



cos

2‘

ðxÞdx;

expand the integrand, and integrate the resulting terms using the reduction formula

cos

ðxÞdx 5

sinðxÞcos

n21

ðxÞ1

n 2 1

cos

n22

ðxÞdx:

Summary of Key Topics 529

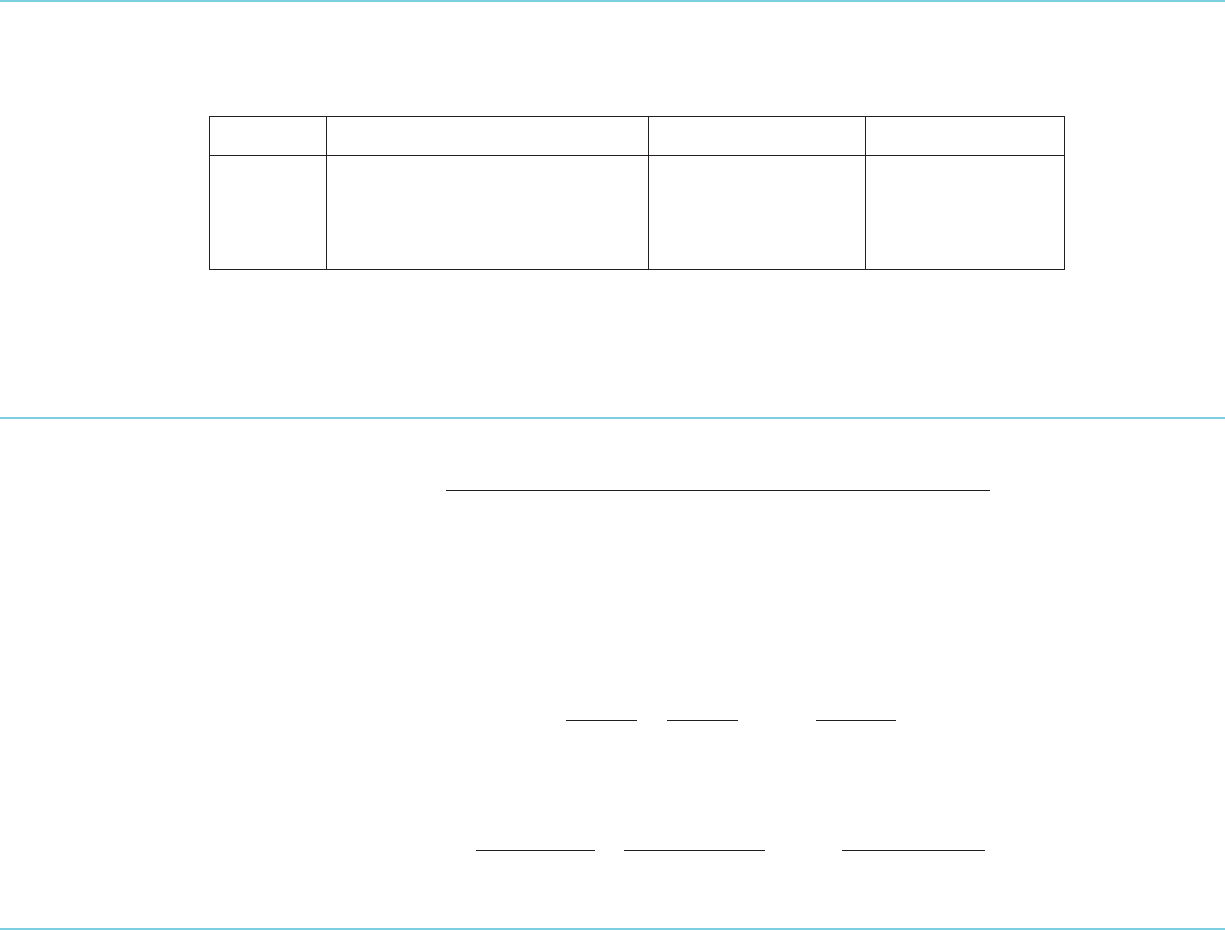
Trigonometric

Substitution

(Section 6.3)

If a is

a positive constant, then we may treat an integrand involving an expression of

the form a

2 x

, a

1 x

,orx

2 a

by making the indirect substitution that is

indicated in the following table:

Expression Substitution Result of Substitution After Simpliﬁcation

2 x

x 5 a sin(θ),dx5 a cos(θ) dθ a



1 2 sin

(θ)



cos

(θ)

1 x

x 5 a tan(θ),dx5 a sec

(θ) dθ a



11 tan

(θ)



sec

(θ)

2 a

x 5 a sec(θ),dx5 a sec(θ) tan(θ) dθ a



sec

(θ) 21



tan

(θ)

To treat an integral that involves the expression

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

αx

1 βx 1 γ

, we complete

the square under the radical. Doing so allows us to write αx

1 βx 1 γ 5 α (a

6 u

)

where u 5 x 1 β /(2α). One of the three trigonometric substitutions listed in the

preceding table may then be applied to a

6 u

Partial Fractions

(Sections 6.4 and 6.5)

To integrate a rational function of the form

pðxÞ

ðx 2 a

ðx 2 a

ðα

1 β

x 1 γ

ðα

‘

1 β

‘

x 1 γ

‘

;

perform the following steps:

1. Be sure that the degree of p is less than the degree of the denominator; if it is

not, divide the denominator into the numerator.

2. Be sure that the quadratic factors are irreducible. Factor them if not.

3. For each of the factors (x 2 a

)

in the denominator of the rational function being

considered, the partial fraction decomposition must contain terms of the form

ðx 2 a

1 1

ðx 2 a

4. For each of the irreducible factors (α

1 β

x1 γ

)

in the denominator of the

integrand being considered, the partial fraction decomposition must contain terms

x 1 C

1 β

x 1 γ

x 1 C

ðα

1 β

x 1 γ

1 1

x 1 C

ðα

1 β

x 1 γ

Improper Integrals

(Sections 6.6, 6.7)

If f (x)

is a continuous function on [a, b) that is unbounded as x -b

, then the

integral

f ðxÞdx is de ﬁned to be

lim

ε-0

b2ε

f ðxÞdx;

provided that this limit exists. A similar deﬁnition is used for functions that are

unbounded at the left endpoint of the interval of integration.

If the singularity occurs in the middle of the interval of integration, then the

integral should be broken up at the singularity to reduce to the two previous cases.

If the integrand is unbounded at both endpoints, then the integral should be broken

up at a chosen point in between to reduce to the two basic cases.

530 Chapter 6 Techniques of Integration

If f is a continuous function on the interval [a,N), then the integral

f ðxÞdx is

deﬁned to be

lim

N-1N

f ðxÞdx

provided that this limit exists. A similar deﬁnition applies to integrals on an interval

of the form (2N, b]. The integral

f ðxÞdx is handled by choosing a point c and

evaluating the sum of the improper integrals

f ðxÞdx and

f ðxÞdx:

Review Exercises for Chapter 6

c In Exercises 1296, evaluate the given deﬁnite integral. b

16xe

2x=2

π=2

4xsinðx=3Þdx

π=2

xcosð2xÞdx

1=3

2xlnð3xÞdx

lnðx=2Þdx

1=2

xsinðxÞdx

10.

π=2

xcosðxÞdx

11.

lnðx=3Þdx

12.

4 xlnðx=2Þdx

13.

14.

π=2

cosðxÞdx

15.

sinðxÞdx

16.

ðxÞdx

17.

π=6



1 1 secðxÞ



18.

π=4



1 1 tanðxÞ



19.

π=4

sin

ð2xÞdx

20.

π=2

2cos

ðx=2Þdx

21.

π=2

π=4

12sin

ðxÞdx

22.

cos

ðx=2Þdx

23.

π=2

sin

ðxÞcos

ðxÞdx

24.

sin

ðx=2Þcos

ðx=2Þdx

25.



cosðxÞ1 sinðxÞ



26.

π=2

sin

ðxÞcos

ðxÞdx

27.

sin

ðxÞcos

ðxÞdx

28.

sin

ðxÞcos

ðxÞdx

29.

π=2

sin

3=2

ðxÞcos

ðxÞdx

30.

π=4

15 sin

ð2xÞcos

ð2xÞdx

31.

π=2

sin

ðxÞcos

ðxÞdx

32.

1=2

cos

ðπxÞdx

33.

2π

sin

ðxÞdx

34.

π=2

π=4

cos

ðxÞsin

ðxÞdt

35.

2π

cos

ðx=4Þdx

36.

cos

ðxÞsin

ðxÞdx

37.

π=3

cos

ðxÞsin

ðxÞdx

38.

π=2

tan

ðx=2Þdx

39.

π=3

sec

ðxÞdx

40.

π=3

tan

ðxÞdx

41.

π=3

sec

ðxÞtan

ðxÞdx

42.

π=3

10 sec

ðxÞtan

ðxÞdx

43.

π=4

2 secðxÞ tan

ðxÞdx

44.

π=4

3 tanðxÞ sec

ðxÞdx

45.

π=4

tanðxÞsec

ðxÞdx

46.

π=4

3 tan

ðxÞsecðxÞ dx

47.

π=4

2 tanðxÞ sinðxÞ dx

48.

π=2

π=4

3 cotðxÞ csc

ðxÞdx

49.

π=2

π=4

4 cotðxÞ csc

ðxÞdx

50.

π=2

π=4

3 cot

ðxÞcscðxÞ dx

51.

π=4

4 sin

ðxÞtanðxÞ dx

52.

π=4

12 cos

ðxÞtan

ðxÞdx

53.

π=4

3 sinðxÞ1 1

1 2 sin

ðxÞ

cosðxÞdx

54.

π=6

5 sinðxÞ2 7

sin

ðxÞ2 3sinðxÞ1 2

cosðxÞdx

55.

1 1 x

1=2

1 1 x

1=4

56.

ﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

Review Exercises 531

57.

ﬃﬃ

1 2 x

58.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 16

59.

ﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

60.

ﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 2 x

61.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

62.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

169 2 x

63.

1=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 4x

64.

ﬃﬃ

2ðx

2 1Þ

23=2

65.

ﬃﬃ

4ð42 x

3=2

66.

ﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 9

67.

ﬃﬃﬃﬃ

2 9

68.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

69.

ð9 1 x

23=2

70.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

71.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

72.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 2 x

73.

2 2 x

74.

2 2 x 2 x

75.

1 1 x

1 2 2x 1 x

76.

2x 1 3

xð1 1 xÞ

77.

2 2x 1 3

xð1 1 x

78.

1 4

1 3x

1 2

79.

2x 1 4

1 2x 1 2

80.

1 5x

2 3x 2 2

81.

1 2x 1 2

ð1 1 x

82.

1 4x

1 4x 1 4

ð1 1 x

Þð2 1 x

83.

1 x

1 2x 1 2

ð1 1 x

Þð2 1 x

84.

1=4

1 1 x

1=2

85.

x 1 x

1=2

86.

x 1 x

1=2

87.

1=2

88.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 2 x

89.

ﬃﬃ

ð82 x

1=3

90.

ﬃﬃﬃ

sinð

ﬃﬃﬃ

Þdx

91.

x expð2x=3Þdx

92.

xln

2=3

ðxÞ

93.

expð2x

Þdx

94.

ð1 1 x

95.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

96.

3x 2 3

1 1

97. Find the area of the region that is bounded above by

y 5 1 2 sin

(x) and below by y 5 cos

(x) for 0 # x # π/2.

98. Calculate the total area of the regions between

y 5 x 2 x

and y 5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

for 0 # x # 1:

99. Find the area of the region that is bounded above by

y 5 ln(1 1 x) and below by y 5 xln(1 1 x) for 0 # x # 1.

100. Find the area of the region that is bounded above by

y 5

ð1 1 x

Þð2 1 xÞ

and below by y 5

ð1 1 xÞð2 1 xÞ

for

0 # x # 1.

532 Chapter 6 Techniques of Integration

GENESIS

DEVELOPMENT6

Each technique of integration that you have learned in

Chapter 6 was discovered early in the history of cal-

culus. The integration by parts formula, to cite one

example, appeared in Leibniz’s ﬁrst development of

calculus (1673). By then, particular instances of inte-

grating by parts had already been published. What

distinguishes the contributions of Leibniz and Newton

is their search for general techniques that could be

applied to a large class of functions. Before their work,

the integration formulas that were known tended to be

isolated results that were discovered in the course of

speciﬁc practical and scientiﬁc investigations. For

example, Kepler discovered the equation

sinðφÞdφ ¼ 1 2 cosðθÞ

because it arose in his study of the orbit of Mars.

Similarly, the formula

secðφÞdφ 5 ln



jsecðθÞ1 tanðθÞj



ð1Þ

became known because of a problem of maritime

navigation.

In 1569, Gerardus Mercator (15121594) introduced

a world map based on a new projection. Prior to

Mercator’s projection, nautical maps were unreliable at

best. The great advantage of the Mercator map is that a

line of constant bearing intersects meridians at constant

angles. But there is a catch: Navigation by the Mercator

map depends on the evaluation of the secant integral

on the left side of equation (1). Two English mathe-

maticians who put to sea on separate naval expeditions

in the late 1500s are known to have performed that

calculation.

When the English Navy needed skilled navigators for

a raid against the Spanish ﬂeet in 1591, the Queen

granted the mathematician Edward Wright (15611615)

a sabbatical from Cambridge so that he could serve on

board a man-of-war. Although the campaign went badly

for the English, Wright survived the ﬁghting. In 1599, he

organized his navigational work into a book titled Cer-

taine Errors of Navigation Corrected. Wright described

one computation as “the perpetual addition of the

secantes answerable to the latitudes of each point or

parallel into the summe compounded of all former

secantes.” Translated into the language of calculus,

Wright approximated the integral

secðφÞdφ by using

Riemann sums in which the increment Δφ was taken to

be one 360th of a degree.

A similar numerical calculation of the secant integral

was carried out a few years earlier by another English

mathematician, Thomas Harriot (15601621), who

served as navigator, cartographer, and surveyor on Sir

Walter Raleigh’s expedition to Virginia in 1585. After

returning to England, Harriot assumed the intellectual

leadership of the circle that assembled around Sir

Walter Raleigh. When Shakespeare wrote

Oh paradox! Black is the badge of hell

The hue of dung eons and the school of night

in Love’s Labour’s Lost (IV, iii, 250), he was referring

to the evening sessions at Raleigh’s country estate

during which Harriot presided over discussions of

astronomy, geography, chemistry, and philosophy. It

was a dangerous circle. One of its members, the poet

and playwright Christopher Marlowe, died in knife-

play over a tavern bill. Raleigh was sentenced for

sedition in 1603, locked up in the Tower of London,

and hanged in 1618. Harriot’s own patron, the Earl of

Northumberland, spent 16 years in prison for his part in

a conspiracy to blow up the English houses of

parliament.

Harriot’s scientiﬁc reputation suffered less from his

own brief incarceration than from the careless dis-

position of his last effects. After his death, Harriot’s

scientiﬁc papers were split among two heirs. One parcel

was soon misplaced. By the time it turned up in 1784,

mixed in among stable accounts, priority for Harriot’s

discoveries had already been claimed by others.

Although some of the papers from the second parcel

were published in 1631, most were lost. His calculation

of the secant integral, for example, remained unknown

until it turned up in the 1960s. Today, Harriot’s most

obvious legacies are the symbols that we use to express

inequalities.

Useful as the calculations of Wright and Harriot

were, an analytic proof of equation (1) was still needed.

One was ﬁnally found by James Gregory in 1668.

However, the famous astronomer Edmund Halley

described Gregory’s derivation as “A long train of

Consequences and Complication of Proportions

whereby the evidence of the Demonstration is in a

great measure lost and the Reader wearied before he

533

attain it.” A few years later, Isaac Barrow, Newton’s

predecessor at Cambridge, published a more satisfac-

tory calculation of the secant integral. Barrow’s argu-

ment went as follows:

secðφÞdφ ¼

cosðφÞ

cos

ðφÞ

dφ 5

cosðφÞ

1 2 sin

ðφÞ

dφ

cosðφÞ

1 2 sinðφÞ

dφ 1

cosðφÞ

1 1 sinðφÞ

dφ



2lnð1 2 sinθÞ1 lnð1 1 sin θÞ





1 1 sinðθÞ

1 2 sinðθÞ



;

which is equivalent to formula (1).

Notice that Barrow’s proof uses the method of par-

tial fractions, a technique that Leibniz systemat ically

used later in the 17th century. The theoretical basis for

the method of partial fracti ons is the Fundamental

Theorem of Algebra. This theorem states that every

nonconstant polynomial with complex coefﬁcients has a

complex root. Such a result was conjectured by Harriot

at the beginning of the 17th century and ﬁnally proved

in 1797 by Carl Friedrich Gauss (17771855), who was

then only 20 years old.

“Archimedes, Newton, and Gauss, these three, are in

a class by themselves among the great mathematicians,

and it is not for ordinary mortals to attempt to range

them in order of merit.” So wrote, E. T. Bell, one of the

most widely read mathematical expositors. Several anec-

dotes suggest that Gauss’s mathematical genius was evi-

dent from early childhood. According to one story, Gauss

was in elementary school when his class was assigned the

task of calculating 1 1 2 1 3 1 ...1 100. Gauss arrived at

the correct answer nearly instantaneously, having already

determined the rule for the sum of an arithmetic

progression.

At the age of 14, Gauss discovered that, for any two

nonnegative numbers a and b, the two sequences

an5 0

ða

n21

1 b

n21

Þ n . 0

and b

bn5 0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

n21

n . 0

have a common limit M (a, b). We call M (a, b) the

arithmetic-geometric mean of a and b. Eight years later,

Gauss proved that

dφ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 k

sin

ðφÞ

Mð1 1 k; 1 2 kÞ

0 # k , 1:

The deﬁnite integral on the left side of Gauss’s equa-

tion is important in several branches of mathematics

and physic s. Although mathematicians had investigated

it since the 1660s, Gauss was the ﬁrst to ﬁnd an effective

method for calculating it.

In 1801, Gauss made a contribution to celestial

mechanics that brought him great fame in scientiﬁc

circles. At the time, seven planets of the solar system

were known, but it was suspected that there was an as

yet undetected planet between the orbits of Mars and

Jupiter. That suspicion arose because of Bode’s law,

which is the approximation B

5 0.4 1 0.3 2

m22

for the

distance in astronomical units (au) between the sun and

the m

planet. This formula works quite well for Venus

through Mars, as the table shows.

From the table we can also see that Bode’s law would

work equally well through Uranus if there was a planet

between Mars and Jupiter, around 2.8 au from the sun.

On the ﬁrst night of the 19th century, January 1st,

1801, Giuseppe Piazzi (17461826) not iced a faint

body that had not been previously catalogued. He

Mercury Venus Earth Mars * Jupiter Saturn Uranus

order from sun 1234*567

m 12345678

0.55 0.7 1 1.6 2.8 5.2 10 19.6

distance to sun 0.39 0.72 1 1.52 * 5.20 9.54 19.18

Table 1: Bode’

s Law and the Seven Known Planets of 1801

534 Chapter 6 Techniques of Integration