Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

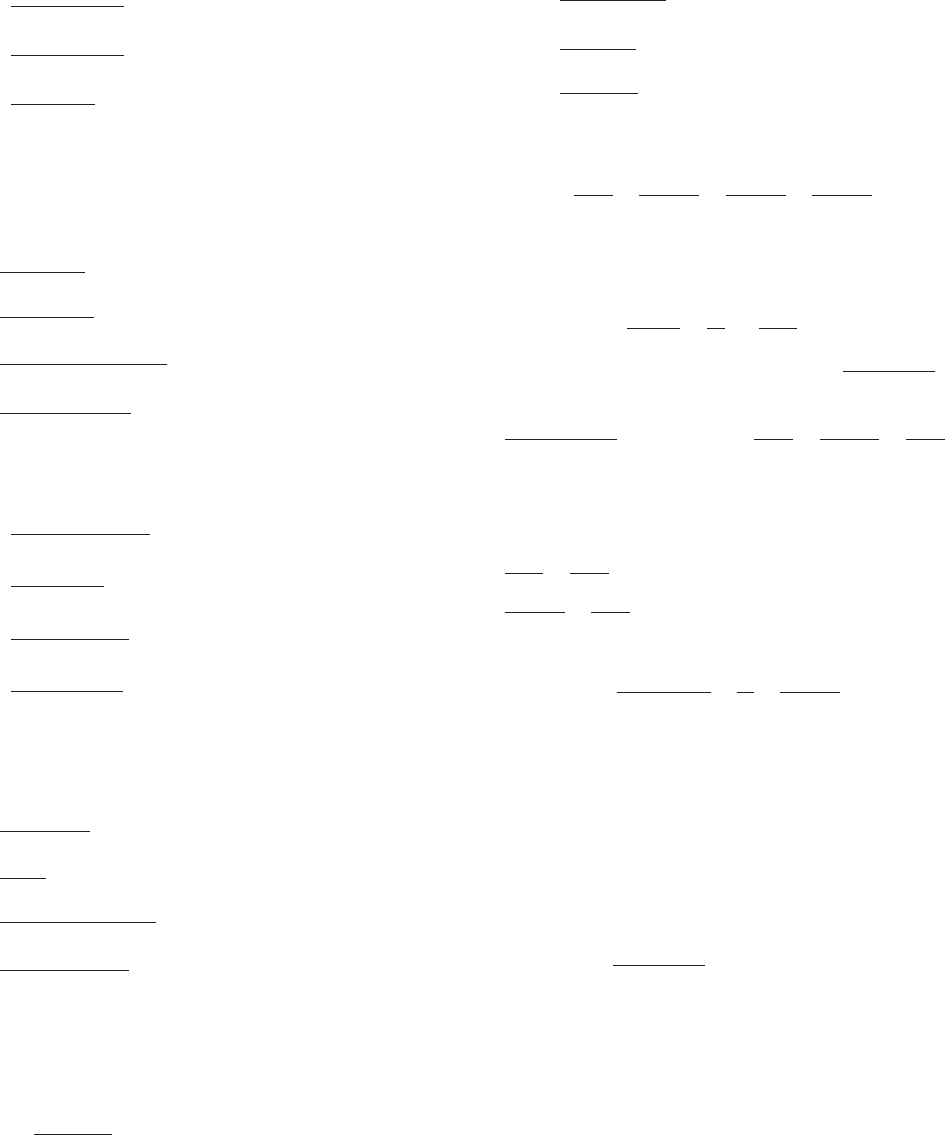
42.

ðx 1 1Þð2x 1 1Þ

43.

1 5x 1 4

xðx 1 1Þðx 1 2Þ

44.

2 2x 2 2

ðx 1 1Þ

Further Theory and Practice

c Calculate each of the indeﬁnite integrals in Exercises

45248. b

45.

1 x 1 2

ðx 1 2Þ

46.

1 5x 1 3

ðx 1 1Þ

47.

2 16x

1 26x 2 14

ðx 2 1Þ

ðx 2 2Þ

48.

1 5x

2 x 2 2

ðx

1 xÞ

c Calculate each of the deﬁnite integrals in Exercises

49252. b

49.

1 6x

1 9x 1 2

xðx 1 1Þ

50.

1 10x 1 1

ðx

2 1Þ

51.

1 8x 1 6

ðx 1 1Þ

ðx 1 2Þ

52.

64x

ðx 1 1Þðx 2 3Þ

c In each of Exercises 53256, make a substitution before

applying

the method of partial fractions to calculate the given

integral. b

53.

expðxÞ

expð2xÞ2 1

54.

x12

2 4

55.

cosðxÞ

sin

ðxÞ2 5sinðxÞ1 6

56.

2lnðxÞ1 5

x ln

xðÞ1 ln xðÞ



c In each of Exercises 57261, two functions f and g are

given.

Calculate

f ðxÞdx by ﬁrst making the substitution

u 5 g (x) and then applying the method of partial fractions. b

57. f ðxÞ5 1=ðx

3=2

2 xÞ; gðxÞ5 x

1=2

58. f ðxÞ5

4=3

2 x

2=3

; gðxÞ5 x

1=3

59. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

ðx 1 1Þ

; gðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

60. f ðxÞ5

ﬃﬃﬃ

1 2

ﬃﬃﬃ

ðx 2 1Þ

; gðxÞ5

ﬃﬃﬃ

61. f ðxÞ5

1=2

2 x

1=6

; gðxÞ5 x

1=6

62. What happens if you attempt a partial fraction decom-

position of 1/(x 2 3)

into

x 2 3

ðx 2 3Þ

(A long calculation should be your last resort.)

63. Assume that a is a positive constant and that jxj, a. Use

the method of partial fractions to derive the formula

2 x



a 1 x

a 2 x



1 C:

64. Find the partial fraction decomposition of

2 3x

1 2

The correct partial fraction decomposition of

1 18x 2 1

ðx 1 4Þ

ðx 2 3Þ

is of the form

x 1 4

ðx 1 4Þ

x 2 3

The values of the coefﬁcients A

, A

, and B are deter-

mined in Example 6. In Exercises 65 and 66, show that the

given incorrect form does not admit a solution for the

unknown coefﬁcients.

65.

x 1 4

x 2 3

66.

ðx 1 4Þ

x 2 3

67. Mr. Woodman set up a partial fraction decomposition

2 4x 1 2

ðx 2 1Þ

and correctly solved A 5 2, B 5 3.

a. What is wrong with his method of solution?

b. Why did the right answer result even though the

method of solution was incorrect?

c. Show that if the numerator is 5x

2 4x 1 1insteadof

2 4x 1 2, then the procedure used will fail. What is

the correct partial fraction decomposition in this case?

Calculator/Computer Exercises

68. Calculate

x 1 3

2 3x

1 3

dx by ﬁnding a partial fraction

decomposition of the integrand. (Find the roots of the

denominator of the integrand numerically. Then use

Heaviside’s method to determine the coefﬁcients of the

partial fraction decomposition.)

69. Let q(x) 5 (x 1 2)(x 1 3)(x 1 5). Find the area of the

region in the ﬁrst quadrant that is bounded on the left

by the y-axis, above by y 5 (2x

1 5)/q(x), and below y 5

1 2)/q(x), and below by y 5 (x

1 2)/q(x).

6.4 Partial Fractions—Linear Factors 505

70. Find the area of the region that is bounded above by the

graph of y 5 ln(x) and below by the graph of y 5 x

1 3x 1 2).

71. Let f(x) 5 4 1 2x 2 x

, let gðxÞ5

1 x 1 2

2 5x

1 6x 2 1

; and

let a be the solution of f(x) 5 g(x) in [0.25, 0.5]. Use a

partial fraction decomposition to ﬁnd the area of the

region bounded above by the graph of y 5 f ( x), a # x # 1

and below by the graph of y 5 g(x), a # x # 1.

c Computer algebra systems can calculate the partial frac-

tion

decomposition of a rational function when the arithmetic

can be done with rational numbers. For example, the Maple

command for obtaining the partial fraction decomposition of

a rational expression R in the variable x is

convertðR; parfrac; xÞ;

In Exercises 72275, use a computer algebra system to ﬁnd the

partial fraction decomposition of the given rational

functions. b

72.

2 9x

1 25x 2 19

2 5x

1 6x

1 4x 2 8

73.

1 10x

1 27x 1 24

1 10x

1 35x

1 50x 1 24

74.

1 2x

2 10x

2 7x

1 9x 2 24

1 2x

2 11x

2 12x 1 36

75.

1 12x

1 17x

1 14x 1 2

1 2x

2 x

2 4x

2 x

1 2x 1 1

6.5 Partial Fractions—Irreducible Quadratic Factors

In Section 6.4, you learned how to evaluate integrals of the form

pðxÞ

ðx 2 a

ðx 2 a

dx; ð6:5:1Þ

where p(x) is a polynomial. To do so, we decomposed the integrand into a sum of

simpler expressions using the method of partial fractions. The purpose of this

section is to extend that technique to denominators that include irreducible

quadratic factors. Because the Fundamental Theorem of Algebra tells us that any

polynomial can be split into a product of linear and irreducible quadratic factors,

our study of the method of partial fractions will therefore be complete. As a result,

we will be able to integrate any rational function p(x)/q(x).

Rational Functions with

Quadratic Terms in the

Denominator

In evaluating integrals of the form (6.5.1), we have made use of two simple alge-

braic expressions: the simple linear building block A/(x 2 a) and the repeated linear

building block A/(x 2 a)

. To ﬁnd a partial fraction decomposition of the rational

function p(x)/q(x) when q(x) has one or more irreducible quadratic factors, we

need two new building blocks.

Simple Quadratic Building Blocks

Bx 1 C

1 bx 1 c

; ð6:5:2Þ

assuming that the denominator ax

1 bx 1 c cannot be factored; otherwise, we would be in the situation of linear

building blocks that we studi ed in Section 6.4. Recall that we learned how to integrate expressions of the form

(6.5.2) in Section 6.3.

Repeated Quadratic Building Blocks

Bx 1 C

ðax

1 bx 1 cÞ

;

where n is an integer greater than 1. Integrands of this form have been treated in Section 6.3. Because n .1we

will have to make certain adjustments in the partial fractions representation.

506 Chapter 6 Techniques of Integration

We can now state our complete partial fractions rule. You will ﬁnd that this

rule just builds upon steps that you are already familiar with: The presence of

irreducible quadratic terms in the denominator does not change the way we treat

the linear terms.

The Method of Partial Fractions

To integrate a rational function of the form

pðxÞ

ðx 2 a

ðx 2 a

ða

1 b

x 1 c

ða

1 b

x 1 c

;

where the factors x 2 a

, x 2 a

,...,x 2 a

, a

1 b

x 1 c

, a

1 b

x 1 c

, ...,a

1 b

x 1 c

are all distinct,

perform the follow ing four steps:

1. Be sure that the degree of the numerator p is less than the degree of the denominator; if it is not, then divide

the denominator into the numerator.

2. Be sure that the quadratic factors a

1 b

x 1 c

cannot be factored into linear factors with real coefﬁcients.

(Do this by verifying that b

2 4a

, 0; if b

2 4a

$ 0 for any quadratic term a

1 b

x 1 c

, then that

expression must be factored into a product of two linear terms.)

3. For each of the factors (x 2 a

)

in the denominator of the rational function being considered, the partial

fraction decomposition must contain terms of the form

ðx 2 a

1 1

ðx 2 a

4. For each of the factors (x

x1c

)

in the denominator of the integrand being considered, the partial

fraction decomposition must contain terms

x 1 C

1 b

x 1 c

x 1 C

ða

1 b

x 1 c

1 1

x 1 C

ða

1 b

x 1 c

The ﬁrst three examples will give you a more concrete idea of how to set up decompositions into partial

fractions (without the distraction of determining the unknown coefﬁcients or performing subsequent

integrations).

⁄ EX

AMPLE 1 State the form of the partial fraction decomposition of

ðx 1 4Þðx 1 5Þ

ðx

1 6Þðx

1 7Þ

Solution The

degree of the denominator is 10. Because the degree of the

numerator is less than 10, division is not needed . The factors of the denominator

include a nonrepeated linear term, x 1 4, and a repeated linear term, (x 1 5)

.Ina

partial frac tion decomposition, the numerators of the summan ds that correspond to

such factors are always constants. Among the factors of the denominator of the

given rational function, we also ﬁnd a nonrepeated irreducible quadratic, x

1 6,

and a repeated irreducible quadratic, (x

1 7)

. In a partial fraction decomposition,

6.5 Partial Fractions—Irreducible Quadratic Factors 507

the numerators of the summands that correspond to such factors are always linear

polynomials. Thus

ðx 1 4Þðx 1 5Þ

ðx

1 6Þðx

1 7Þ

x 1 4

x 1 5

ðx 1 5Þ

Ex 1 F

1 6

Gx 1 H

1 7

Ix 1 J

ðx

1 7Þ

Notice that the number of unknown factors in the numerators is 10, which is the same

as the degree of the denominator polynomial in the original rational function.

Checking for

Irreducibility

It is very important to begin with the right form of a partial fraction decomposition

before attempting to solve for the unknown coefﬁcients. Usually, it is impossible to

solve for the unknown coefﬁcients when the partial fraction decomposition has not

been set up correctly.

⁄ EX

AMPLE 2 Find the correct form of the partial fraction decomposition

for the rational expression

1 11x 1 10

ðx 1 1Þðx

1 4x 1 3Þ

Solution Because

the degree of the numerator is 2 and the degree of the

denominator is 3, a preliminary divi sion is not necessary. Notice that the correct

partial fraction decomposition is not

1 11x 1 10

ðx 1 1Þðx

1 4x 1 3Þ

x 1 1

Bx 1 C

1 4x 1 3

: ð6:5:3Þ

The reason is that we have not factored the denominator as far as possible. The

quadratic polynomial x

1 4x 1 3 factors as

1 4x 1 3 5 ðx 1 1Þðx 1 3 Þ:

Thus the given rational function really falls under the case of distinct linear factors,

which we studied in Section 6.4. The correct form of the partial fraction decom-

position is

1 11x 1 10

ðx 1 1Þðx

1 4x 1 3Þ

1 11x 1 10

ðx 1 1Þ

ðx 1 3Þ

x 1 1

ðx 1 1Þ

x 1 3

: ð6:5:4Þ

You may want to practice the methods of determining the unknown coefﬁcients

that we studied in Section 6.4. You will ﬁnd that the values A 5 2, B 5 1, and C 5 1

turn equation (6.5.4) into an identity in x. By contrast, there are no values of A, B,

and C for which equation (6.5.3) is an identity in x.

INSIGHT

Remember that the Quadratic Formula tells us whether a quadratic factor

1 bx 1 c is irreducible or not. If the discriminant b

2 4ac is negative, then the

polynomial is irreducible; otherwise, it can be factored into linear terms. A quick

calculation of the discriminant of x

1 4x 1 3 in Example 2 would result in the positive

number 4

2 4  1  3 5 4. That would alert us to the reducibility of x

1 4x 1 3.

⁄ EXAMPLE 3 Find the correct form of the partial fraction decomposition

of 3/(x

1 1).

Solution This

expression may appear to have an irreducible denominator, but it

does not. Cubic (and higher-degre e) polynomials are never irreducible. Notice

508 Chapter 6 Techniques of Integration

that 21 is a root of the polynomial x

1 1. Therefore (x 1 1) is a divisor. After

performing the polynomial division, we ﬁnd that

1 1 5 ðx 1 1Þðx

2 x 1 1Þ:

The quadratic factor has negative discriminant (21)

2 4  1  1 523, so it is

irreducible. Thus we see that the correct partial fraction decomposition for our

rational expression is

1 1

x 1 1

Bx 1 C

2 x 1 1

: ð6:5:5Þ ¥

INSIGHT

It is important for you to realize that the Fundamental Theorem of

Algebra guarantees that any real polynomial can be factored into linear and quadratic

factors. In the theory of partial fractions, we never have to use building blocks that

involve irreducible cubic, quartic, or higher order factors—they do not exist.

Calculating the

Coefﬁcients of a

Partial Fraction

Decomposition

Now that we have considered the forms that decompositions into partial fracti ons

can take, let us see how the unknown coefﬁcients can be computed in practice.

⁄ EX

AMPLE 4 Find the partial fraction decomposition of the rational

function 3/(x

1 1).

Solution In

equation (6.5.5) of Example 3, we determined the correct form of the

partial fraction decomposition of 3/(x

1 1). The right side of equation (6.5.5) can

be written as

Aðx

2 x 1 1Þ1 ðBx 1 CÞðx 1 1Þ

ðx 1 1Þðx

2 x 1 1Þ

or, after expanding both the numerator and denominator,

ðA 1 BÞx

1 ð2A 1 B 1 CÞx 1 ðA 1 CÞ

1 1

The numerator of this expression must eq ual the numerator of the left side of

(6.5.5):

1 0x 1 3 5 ðA 1 BÞx

1 ð2A 1 B 1 CÞx 1 ðA 1 CÞ:

Equating the coefﬁcients of like powers of x on each side of this equation leads to

the simultaneous equations

A 1 B 5 0; 2A 1 B 1 C 5 0; A 1 C 5 3:

The ﬁrst equation allows us to replace B with 2A in the second equation to

obtain 22A 1 C 5 0. Thus C 5 2A. The third equation then tells us that A 1 (2A) 5

3orA 5 1. Consequently, B 52A 521andC 5 2A 5 2. In conclusion, the partial

fraction decomposition is

1 1

x 1 1

2x 1 2

2 x 1 1

: ¥

⁄ EX

AMPLE 5 Calculate

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

dx:

6.5 Partial Fractions—Irreducible Quadratic Factors 509

Solution The degree of the denominator is 4, one greater than the degree of the

numerator. Division is therefore not necessary. Because the discriminants of x

1 4x 1 5

and x

1 9 are negative numbers, 4

2 4  1  5 524and0

2 4  1  9 5236,

respectively, we can be sure that further factoring of the denominator is impossible.

We may therefore proceed directly to the partial fraction decomposition:

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

Ax 1 B

1 4x 1 5

Cx 1 D

1 9

We combine the two summands on the right to obtain

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

ðAx 1 BÞðx

1 9Þ1 ðCx 1 DÞðx

1 4x 1 5Þ

ðx

1 4x 1 5Þðx

1 9Þ

ðA 1 CÞx

1 ðB 1 4C 1 DÞx

1 ð9A 1 5C 1 4DÞx 1 ð9B 1 5DÞ

ðx

1 4x 1 5Þðx

1 9Þ

We may now equate the numerators on the left with the numerator on the right:

2 x

2 3x 1 3 5 ðA 1 CÞx

1 ðB 1 4C 1 DÞx

1 ð9A 1 5C 1 4DÞx 1 ð9B 1 5 DÞ:

By equating coefﬁcients of like powers of x, we obtain the four equations

A 1 C 5 1; B 1 4C 1 D 521; 9A 1 5C 1 4D 523; 9B 1 5D 5 3:

We may use the ﬁrst and second of these equations to solve for A and B in terms of

C and D. We obtain A 5 1 2 C and B 521 2 4C 2 D. By us ing these expressions in

C and D to replace A and B in the third and fourth equations, we obtain two

equations in the two unknowns C and D. Thus we have

9ð1 2 CÞ1 5C 1 4D 523; or 2 4C 1 4D 5212

9ð21 2 4C 2 DÞ1 5D 5 3; or 236C 2 4D 5 12 :

We solve these last two equations in C and D, obtaining C 5 0 and D 523. It

follows that A 5 1 2 C 5 1 2 0 5 1 and B 521 2 4C 2 D 521 2 4(0) 2 (23) 5 2.

Thus

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

x 1 2

1 4x 1 5

1 9

and

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

dx 5

x 1 2

1 4x 1 5

dx 2

1 9

dx: ð6:5:6Þ

We complete the square x

1 4x 1 5 5 (x 1 2)

1 1 and make the substitution

u 5 x 1 2, du 5 dx to convert the ﬁrst integral on the right side of equation (6.5.6) to

1 1

du:

By means of the substitution w 5 u

1 1, dw 5 2udu, this last integral is converted to

dw 5

ln ðjwjÞ1 C:

We resubstitute, observing that w 5 u

1 1 5 x

1 4x 1 5 is positive, to obtain

510 Chapter 6 Techniques of Integration

x 1 2

1 4x 1 5

dx 5

ln ðx

1 4x 1 5Þ1 C:

Finally, we use formula (6.3.2) to see that

3=ðx

1 9Þdx 5 arctanðx=3Þ1 C. After

substituting for the two integrals on the right side of equation (6.5.6), we have

2 x

2 3x 1 3

ðx

1 4x 1 5Þðx

1 9Þ

dx 5

lnðx

1 4x 1 5Þ2 arctan





1 C: ¥

⁄ EX

AMPLE 6 Calculate the integral

x 2 1

xðx

1 1Þ

dx:

Solution The

degree of the numerator is less than that of the denominator, so we

proceed directly to the partial fraction decomposition:

x 2 1

xðx

1 1Þ

Bx 1 C

1 1

Dx 1 E

ðx

1 1Þ

Putting the right side over a common denominator leads to

x 2 1 5 Aðx

1 1Þ

1 ðBx 1 CÞðx

1 1Þx 1 ðDx 1 EÞx

5 Aðx

1 2x

1 1Þ1 ðBx 1 CÞðx

1 xÞ1 Dx

1 Ex

5 x

ðA 1 B Þ1 x

ðCÞ1 x

ð2A 1 B 1 DÞ1 xðC 1 EÞ1 A:

Equating like coefﬁcients of x leads to the system

A 1 B 5 0

C 5 0

2A 1 B 1 D 5 0

C 1 E 5 1

A 521.

We conclude that A 521, B 5 1, C 5 0, D 5 1, E 5 1. Therefore

x 2 1

xðx

1 1Þ

dx 5

dx 1

1 1

dx 1

x 1 1

ðx

1 1Þ

dx;

x 2 1

xðx

1 1Þ

dx 52lnðjxjÞ1

1 1

dx 1

ðx

1 1Þ

dx 1

ðx

1 1Þ

dx: ð6:5:7Þ

The ﬁrst and second integrals on the right side are handled with the substitution

u 5 x

1 1, du 5 2xdx. The results of these integrations are

1 1

dx 5

lnðx

1 1Þ1 C and

ðx

1 1Þ

dx 5 C 2

1 1

: For the last integral on the right

side of equation (6.5.7), we make the substitution x 5 tan (θ), dx 5 sec

(θ)dθ. This

substitution converts the integral into

sec

ðθÞ



tan

ðθÞ1 1



dθ 5

sec

ðθÞ

sec

ðθÞ

dθ 5

sec

ðθÞ

dθ 5

cos

ðθÞdθ 5

ð6:2:6Þ

θ 1

sinðθÞcosðθÞ1 C:

6.5 Partial Fractions—Irreducible Quadratic Factors 511

After resubstituting for x, we have

ðx

1 1Þ

dx 5

arctanðxÞ1

1 1

1 C:

Assembling all the pieces, we conclude that our original integral calculat es to

x 2 1

xðx

11Þ

dx 52lnðjxjÞ1



lnðx

1 1Þ2

ðx

1 1Þ

ðx

1 1Þ

1 arctanðxÞ



1 C:

QUICK QUIZ

1. True or false: If q(x) is a polynomial of degree n that factors into irreducible

quadratic terms and if p(x) is a polynomial of degree m with m , n, then an

explicitly calculated partial fraction decomposition of p(x)/q(x) requires the

determination of n unknown constants.

2. What is the form of the partial fraction decomposition of

ðx

2 3x 2 4Þðx

2 3x 1 4Þ

3. What is the form of the partial fraction decomposition of

1 1

ðx

1 1Þðx

1 4Þ

4. What is the form of the partial fraction decomposition of

1 1

ðx

1 4Þ

Answers

1. True 2.

x 1 1

x 2 4

Cx 1 D

2 3x 1 4

Ax 1 B

1 1

Cx 1 D

1 4

Cx 1 D

1 4

Ex 1 F

ðx

1 4Þ

EXERCISES

Problems for Practice

c In each of Exercises 1210, write down the form of the

partial fraction decomposition of the given rational function.

Do not explicitly calculate the coefﬁcients. b

1 x 1 1

ðx

1 1Þðx

1 4Þ

ðx

1 2x 1 2Þð2x

1 5x 1 3Þ

1 x 1 1

ðx

1 1Þðx

1x11Þ

ðx

1 1Þð5x

1 4x 1 1Þ

2x 1 1

ðx

1 x 1 3Þðx 2 4Þ

1 x 1 1

ðx11Þ

ðx

14Þ

ðx 2 2Þ

1 x 1 1

ðx

2 1Þ

1 x 1 1

ðx

2 1Þðx

1 1Þ

10.

ðx 2 3Þ

ðx

1 6x 1 10Þ

c In each of Exercises 11220, explicitly calculate the partial

fraction decomposition of the given rational function. b

11.

2 5x 1 4

ðx 2 1Þðx

1 1Þ

12.

1 2

ðx

1 1Þx

13.

2 3x

1 9x 2 6

ðx

1 2Þðx

1 1Þ

14.

1 2x

ðx

1 1Þ

15.

2 x

ðx

1 1Þ

512 Chapter 6 Techniques of Integration

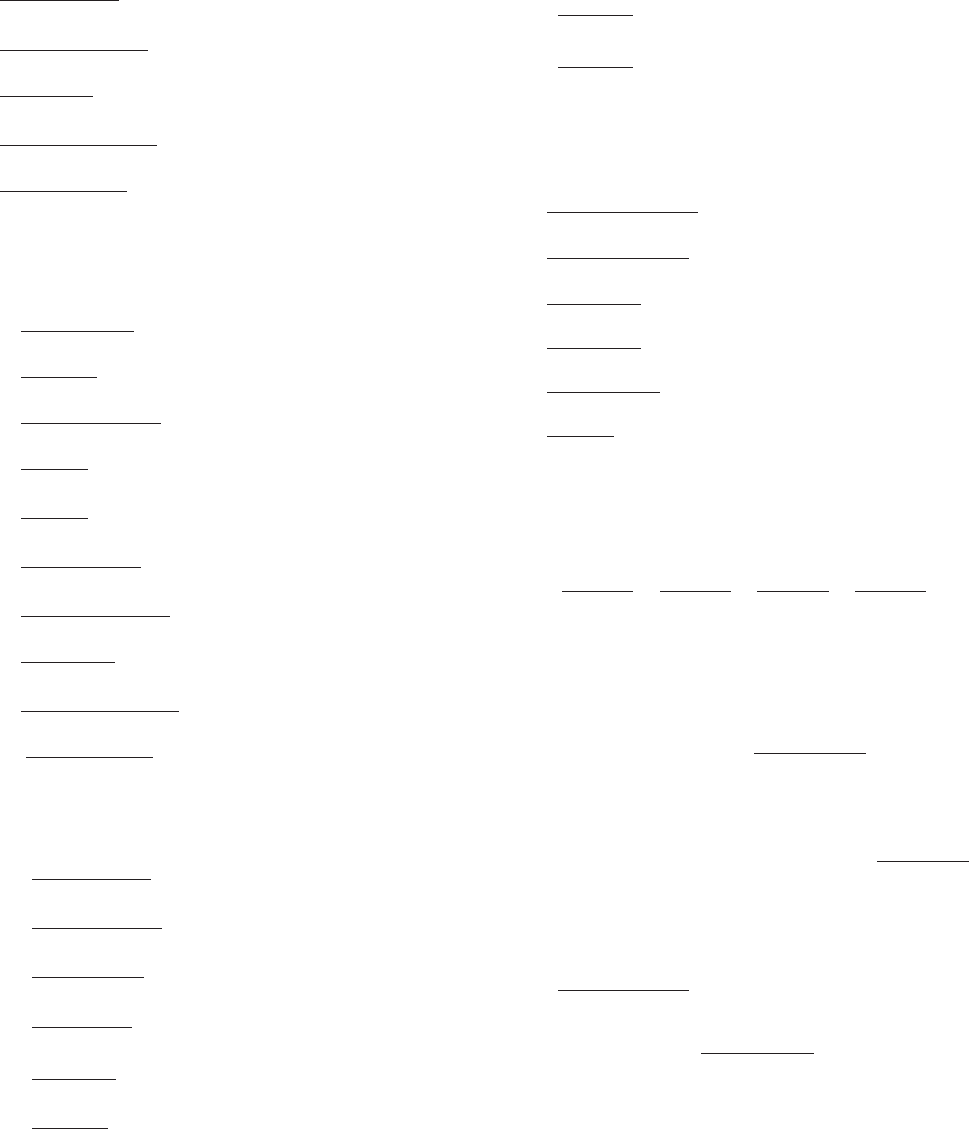
16.

ðx 1 1Þ

ðx

1 1Þ

17.

1 12x

2 9x 1 48

ðx 2 3Þðx

1 4Þ

18.

1 4x 1 2

ðx

11Þ

19.

2 5x

1 10x 2 19

ðx

1 4Þðx

1 3Þ

20.

1 15x

1 30

ðx

1 4Þðx

1 3Þ

c In each of Exercises 21230, use the method of partial

fractions to decompose the integrand. Then evaluate the

given integral. b

21.

2 5x 1 4

ðx 2 1Þðx

1 1Þ

22.

1 2

ðx

1 1Þx

23.

1 9x 2 3x

2 6

ðx

1 2Þðx

1 1Þ

24.

1 2x

ðx

1 1Þ

25.

2 x

ðx

1 1Þ

26.

ðx 1 1Þ

ðx

1 1Þ

27.

1 12x

2 9x 1 48

ðx 2 3Þðx

1 4Þ

28.

1 4x 1 2

ðx

1 1Þ

29.

2 5x

1 10x 2 19

ðx

1 4Þðx

1 3Þ

30.

1 15x

1 30

ðx

1 4Þðx

1 3Þ

c In each of Exercises 31238, evaluate the given deﬁnite

integral. b

31.

1 3

ðx

1 1Þðx

1 2Þ

32.

2 x

1 2x 1 1

ðx

2 1Þðx

1 1Þ

33.

1 4x 1 6

ðx 1 1Þðx

1 2Þ

34.

1 8x

1 3

xðx

11Þ

35.

2 x 1 2

xðx

1 1Þ

36.

1 6

ðx

1 1Þ

37.

1 x 1 1

ðx

1 1Þ

38.

1 x 1 1

ðx

1 1Þ

Further Theory and Practice

c In Exercises 39244, calculate the given integral. b

39.

1 6x 1 4

ðx 1 1Þðx

1 2x 1 2Þ

40.

1 5x 1 3

ðx 1 1Þðx

1 x 1 1Þ

41.

1 4x 1 9

2 1

42.

2 2x 1 2

1 1

43.

2 x

2 x 1 1

44.

ðx

1 1Þ

45. Show that equation (6.5.3) is not an identity in x for any

values of A, B, and C.

46. What happens if you attempt a partial fraction decom-

position of 1/(x

1 3)

into

x 1 B

1 3

x 1 B

ðx

1 3Þ

x 1 B

ðx

1 3Þ

x 1 B

ðx

1 3Þ

(Brute force calculation should be a last resort.)

Calculator/Computer Exercises

47. Let b be the abscissa of the point of intersection of the

graphs of y 5 x

1 2 and y 5

1 3x 1 2

1 x

1 x 1 1

for 0 , x , 1.

Calculate the area of the region between the two curves

for 0 # x # b.

48. Let b be the abscissa of the ﬁrst-quadrant point of inter-

section of the graphs of y 5 x

and y 5

1 4x

1 3x

1 2

Calculate the area of the region between the two curves

for 0 # x # b.

49. Find the area of the region in the ﬁrst quadrant that is

bounded above by y 5 1 2 x

and below by

y 5

1 4x 1 5

1 3x

1 7x 1 5

50. Find the four points of intersection of the curves

y 5 1 2 x

/16 and y 5

1 x

1 x 1 2

1 3x

1 2

. Let a be the least

abscissa of these points and b the greatest. Calculate the

total area of the regions that are bounded above by one of

the curves and below by the other for a # x # b.

6.5 Partial Fractions—Irreducible Quadratic Factors 513

6.6 Improper Integrals—Unbounded Integrands

The theory of the integral that you learned in Chapter 5 enables you to integrate a

continuous function f (x) on a closed, bounded interval [a, b]. However, often it is

necessary to integrate an unbounded function, or a function that is deﬁned on an

unbounded interval. In this section and the next, you learn to do so.

Integrals with Inﬁnite

Integrands

Let f be a continuous function on the interval [a, b). Suppose that f is unbounded

as x approaches b from the left side (see Figure 1). It can be shown that the

Riemann sums of an unboun ded function do not have a limit as the order of the

uniform partition tends to inﬁnity. In other words, f does not have a Riemann

integral over the interval [a, b]. We say that

f ðxÞdx is an improper integral with

inﬁnite integrand at b. Figure 2 illustrates the method by which we deﬁne and

evaluate this type of integral. The idea is to integrate almost up to the singularity —

within ε—and then to let ε tend to 0. Thus let ε be a small positive number. Because

f is continuous on the interval [a, b 2 ε ], we can form the Riemann integral

b2ε

f ðxÞdx. Now we let the upper limit of integration, b 2 ε, ap proach b, which is

the same thing as letting ε tend to 0. Recall that we write this limit as ε - 0

because ε approaches 0 through positive values. If the limit exists, then we say that

the improper integral converges. Otherwise we say it diverges.

DEFINITION

If f (x) is continuous on [a, b), and unbounded as x approaches b

from the left, then the value of the improper integral

f ðxÞdx is deﬁned to be

f ðxÞdx 5 lim

ε-0

b2ε

f ðxÞdx; ð6:6:1Þ

provided that this limit exists and is ﬁnite. In this case, we say that the improper

integral converges. Otherwise, the integral is said to diverge.

⁄ EX

AMPLE 1 Evaluate the integral

ð8 2 xÞ

21=3

dx:

Solution The

given inte gral is improper with inﬁnite integrand f (x) 5 (8 2 x)

21/3

as x approaches 8. Usin g the antiderivative FðxÞ52

ð8 2 xÞ

2=3

ð8 2 xÞ

2=3

f (x) on the interval [0, 8), we calculate

ð8 2 xÞ

21=3

dx 5 lim

ε-0

82ε

ð8 2 xÞ

21=3

dx 5 lim

ε-0



ð8 2 xÞ

2=3



82ε



lim

ε-0



2=3

2 8

2=3



ð0 2 4Þ5 6:

We conclude that the given improper integral is convergent and its value is 6.

INSIGHT

In Example 1, we calculate the antiderivative F(x)off (x) 5 (8 2 x)

21/3

and apply the Fundamental Theorem of Calculus on the closed interval [0, 8 2 ε]. We are

justiﬁed in doing so because f is continuous on that interval. However, because f is not

m Figure 1 The line x 5 b is a

vertical a asymptote.

b  e

m Figure 2 The improper inte-

gral

f ðxÞdx is deﬁned to be the

limit of the area of the shaded

region as b 2 ε approaches b.

514 Chapter 6 Techniques of Integration