Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

continued to watch it until it faded from his sight on

February 11, 1801. Piazzi had tracked it for 41 nights

over an arc of only 3



. In June of 1801, he published his

observations, but they did not help other astronomers

relocate the object, which was thought to be the

undiscovered planet predicted by Bode’s law.

Where astronomers with telescopes failed, Gauss

succeeded, using mathematics alone. In particular, Gauss

applied a mathematical tool of his own invention—the

Method of Least Squares. On December 7, 1801, the ﬁrst

clear viewing night after Piazzi’s object emerged from

the shadow of the sun, it was spotted exactly where

Gauss had predicted it would be. As Gauss remarked,

“the fugitive was restored to observation.” (Piazzi’s

object, however, turned out to be only an asteroid, and

Bode’s law is now known to be invalid.)

Many descendants of Gauss are scattered across the

United States. The two youngest of his four sons,

Eugen and Wilhelm, emigrated to the United States.

Writing from New York City in 1831, Eugen informed

his father that “Your na me is well known even he re in

this wilderness.” Eugen’s army enlistment took him to

Fort Snelling, Minnesota, where he served under the

command of future president General Zachary Taylor.

He settled in St. Charles, Missouri, where the house

that he built still stands.

Genesis & Development 535

This page intentionally left blank

CHAPTER 7

Applications of

the Integral

There is a common philosophical thread that runs through the ﬁrst ﬁve sections of

this chapter. Namely, in each of these sections, we introduce certain physical

quantities. We approximate these quantities in a plausible way by a mathematical

procedure that leads to a Riemann sum. By letting the subinterval lengths that

appear in the sum tend to 0, we are in each case led to an integral. We then declare

that integral to, in fact, represent the physical quantity that we started out to

analyze. What gives us the right to do this?

There is a good pract ical answer. In each of the instances discussed in this

chapter, the mathematical model for the physical quantity being discussed gives the

same measurement in practical examples as one or more independent methods. For

instance, we develop several mathematical formulas for the volumes of solids of

revolution. When applied to calculate the volume inside a sphere, the formula

generates the same an swer as can be obtained by immersing a sphere in water and

measuring the displacement. We also develop a formula for the length of a curve.

In practice, this formula gives the same answers as one obtains when measuring the

length of the same curves with a tape measure. Similar comments apply to the other

physical quantities—work and center of mass—which are discussed here.

When applying mathematics, it is always important to have objective methods

for testing the validity of the mathematical models. Scientists are constantly

challenging, checking, and revising their methods for modeling. This is a crucial

step in the advancement of scientiﬁc knowled ge.

In the last two sect ions of this chapter, you learn methods that enable you to

determine an unknown function y(x) from information about its rate of change. In

these applications, the star ting point is a model for the derivative of the function.

We deduce or obs erve an equation involving x, y(x), and y

(x). Such a relationship

is called a differential equation. The integral is then used to solve the differential

equation and ﬁnd a formula for the function itself. Solving differential equations

constitutes one of the most important applications of calculus. For many students, a

specialized course in differential equations is the natural continuation of thei r

calculus studies.

PREVIEW

537

7.1 Volumes

In this section, we will think about volume in much the same way that we thought

about area in Chapter 5. That is, we will be calculating the volume of a solid by

cutting up the solid into elementary piece s.

Volumes by Slicing—

The Method of Disks

You may have already learned that

V 5

πr

h ð7:1:1Þ

is the formula for the volume V of a right circular cone of height h and radius r

(Figure 1). Let us see for ourselves how we can deduce this formula. We begin by

slicing up the cone into N equally thick pieces as in Figure 2. The volume of each

slice is approximately equal to the volume of a disk—see Figure 2. If the j

disk has

radius r

and thickness Δx, then its volume is the product (πr

) Δx of its cross-

sectional area πr

and its thickness Δx. To obtain an approximation to the volume

of the cone, we add up the volumes of the disks:

j 5 1

πr

Δx: ð7:1:2Þ

To get a better approximation, we make the disks thinner by increasing the value of

N. To get the precise volume V, we let the thickness of the disks tend to 0 by letting

N tend to inﬁnity:

V 5 lim

N-N

j51

πr

Δx: ð7:1:3Þ

To compute this limit, we identify expression (7.1.2) as a Riemann sum. Then

formula (7.1.3) expresses the volume of the cone as a limit of Riemann sums—that

is to say, an integral (as you learned in Chapter 5). Example 1 provides the details

of the technique just described.

⁄ EX

AMPLE 1 Calculate the volume V of a right circular cone that has

height 11 and base of radius 5.

Solution Figure

3 depicts the xy-plane and the cone in question. The cone is

positioned so that the x-axis is its axis of symmetry, and the origin is the center of its

base. The line segment that is formed by the intersection of the edge of the cone

m Figure 1

jth slice

x

m Figure 2 A disk is used to approximate a slice

of the cone.

538 Chapter 7 Applications of the Integral

and the xy-plane has slope 25/11 and y -intercept (0, 5) . Its equation is therefore

y 525x/11 1 5.

In Figure 3, we have partitioned the interval [0, 11] into N subint

ervals of equal

length Δx. For each j from 1 to N, a point s

is chosen in the j

subinterval.

(Because the particular value of s

will not matter, a formula for s

is not needed.)

As Figure 3 indicates, we approximate the j

slice by means of a disk of thickness

Δx and radius r

equal to the vertical distance from the point (s

, 0) to the edge of

the cone. The approximating sum (7.1.2) becomes

j51



25s

1 5



 Δx: ð7:1:4Þ

As N increases and Δx becomes smaller, this sum gives a more accurate approx-

imation to the desired volume; however, expression (7.1.4) is also a Riemann sum

for the integral



25x

1 5



dx: ð7:1:5Þ

Thus both the volume V of the cone and the integral (7.1.5) are equal to the

limit of sum (7.1.4) as N tends to inﬁnity. We conclude that V is equal to



25x

1 5



dx 5 π





ð2x 1 11Þ

dx 5 π





ð2x 1 11Þ



5 π









π  5

 11: ¥

INSIGHT

In Example 1, if we replace each occurrence of 5 with r and each 11 with h,

then formula (7.1.5) becomes



2rx

1 r



dx, and we ﬁnd that the volume of the

right circular cone with base r and height h is

V 5



2rx

1 r



dx 5 π





ð2x 1 hÞ

dx 52





ð2x 1 hÞ



x5h

x50

πr

as given in formula (7.1.1).

y    5

 

 5

jth slice

x

m Figure 3

7.1 Volumes 539

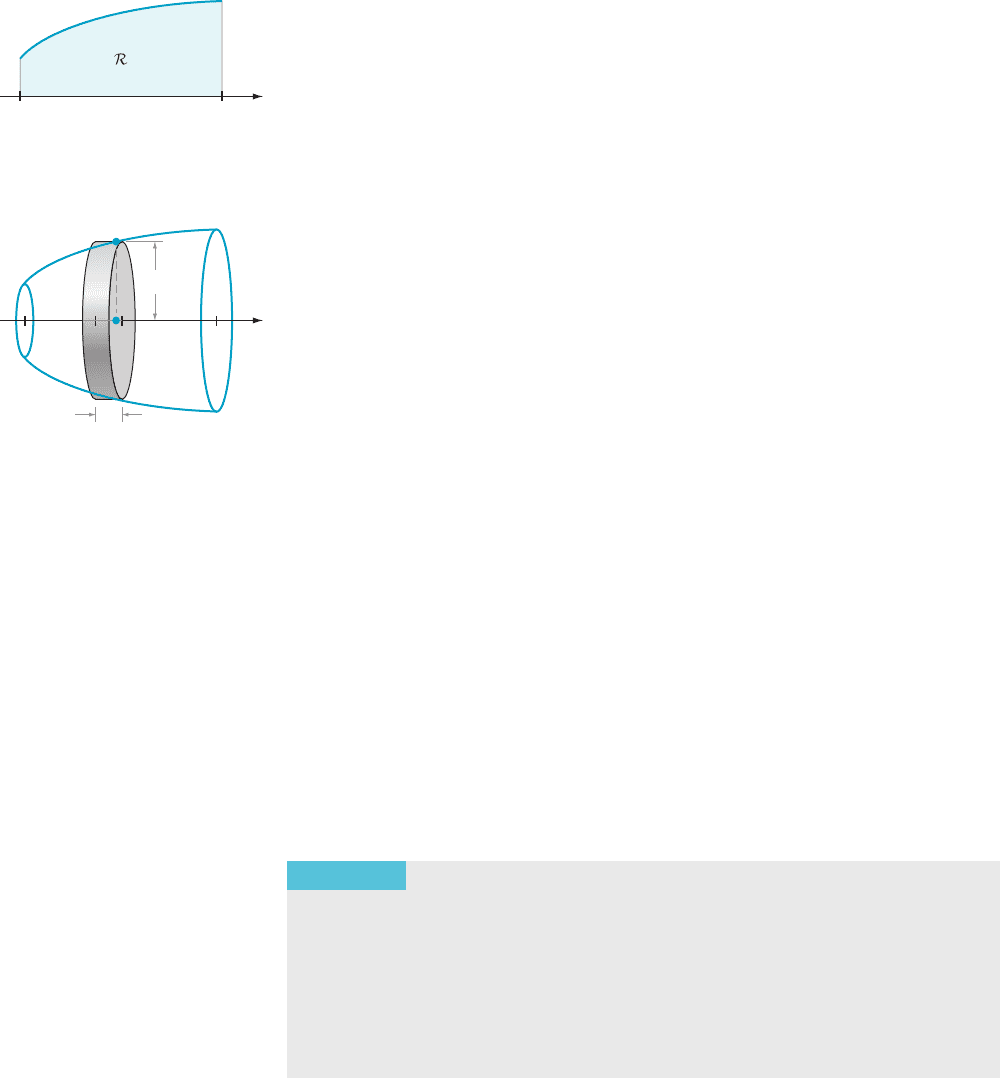
Solids of Revolution With little modiﬁcation, the method that we have developed for the cone can be

used to ﬁnd the volumes of other solids. Glance again at Figure 3. The key step is to

recognize that, if R is the region in the xy-plane that lies below the graph of

y 525x/11 1 5 and above the interval [0, 11], then the solid cone can be generated

by rotating R about the x-axis. In general, a solid that is obtained by rotating a

ﬁgure in the xy-pla ne about a line in the xy-plane is called a solid of revolution.

Consider, for example, a nonnegative continuous function f that is deﬁned on

an interval [a, b]ofthex-axis. The graph of f, the x-axis, and the vertical lines x 5 a

and x 5 b bound a region R in the plane, as shown in Figure 4. Let us see how to

calculate the volume of the solid of revolution that is generated by rotating the

planar region R about the x-axis.

As before, we partition the interval [a, b] into N subinterval s of equal length

Δx. For each j from 1 to N, we choose a point s

in the j

subinterval. Figure 5

indicates that we approximate the j

slice of the solid of revolution with a disk of

radius f ( s

) and thickness Δx. The contribution to volum e from this disk is the

product of its cross-sectional area and thickness, or (π f (s

)

) Δx. The sum of the

volumes of the N disks is

j51

π f ðs

 Δx:

As we let N tend to inﬁnity, the union of the approximating disks becomes closer to

the solid of revolution. We therefore deﬁne the volume V of the solid of revolution

to be

V 5 lim

N-N

j51

π f ðs

 Δx:

Notice that the expression in this limit is a Riemann sum for the integral

π f ðxÞ

dx:

Because

π f ðxÞ

dx 5 lim

N-N

j51

π f ðs

 Δx;

we see that the volume of the solid of revolution is represented by a Riemann

integral. We may state our conclusion as a theorem.

THEOREM 1

(Method of Disks: Rotation About the x-Axis) Suppose that f is a

nonnegative, continuous function on the interval [a, b]. Let R denote the region

of the xy-plane that is bounded above by the graph of f, below by the x-axis, on

the left by the vertical line x 5 a, and on the right by the vertical line x 5 b. Then,

the volume V of the solid obtained by rotating R about the x-axis is given by

V 5 π

f ðxÞ

dx:

y  f(x)

m Figure 4

, f(s

))

f(s

)

x

y  f(x)

m Figure 5

540 Chapter

7 Applications of the Integral

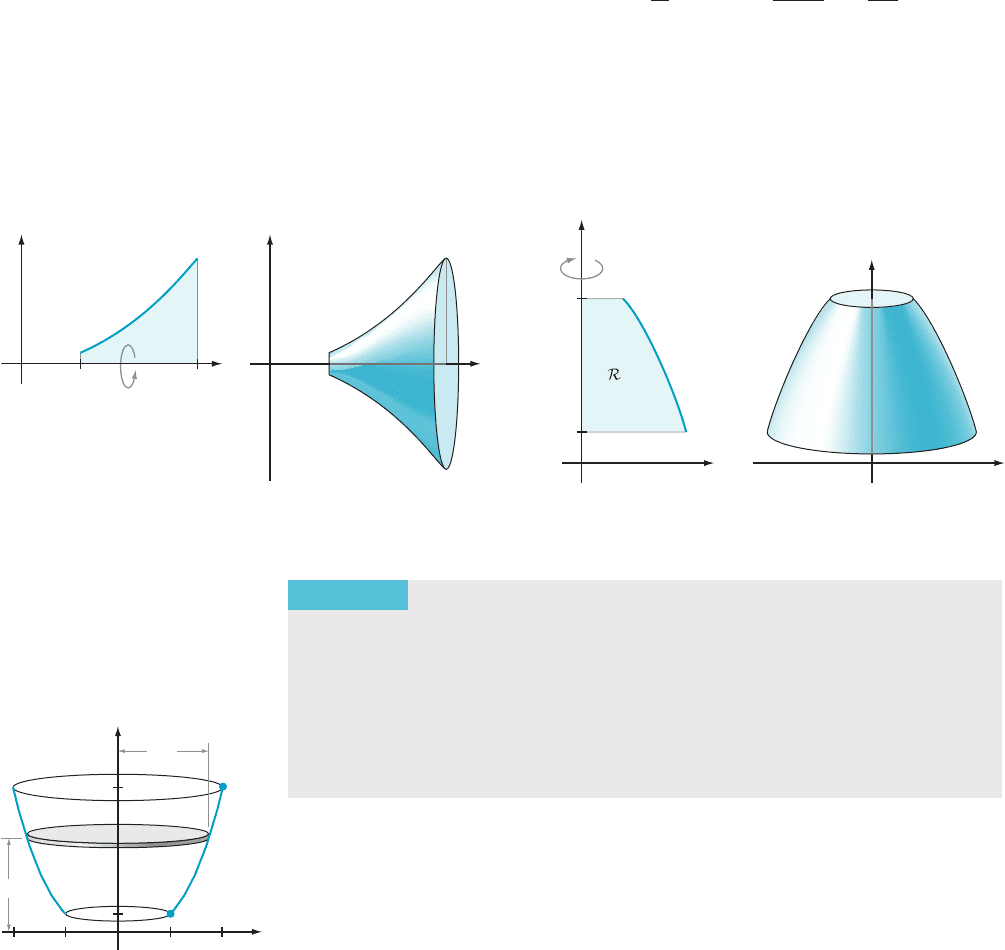
⁄ EXAMPLE 2 Calculate the volume of the solid of revolution that is gen-

erated by rotating about the x-axis the region of the xy-plane that is bounded by

y 5 x

, y 5 0, x 5 1, and x 5 3.

Solution Figure

6 shows the region to be revolved as well as the solid of revolution.

According to Theorem 1, the volume of this solid is

V 5 π

ðx

dx 5 π





x53

x51



5 π



2 1



242

π: ¥

In some problems, it is useful to think of the curve as x 5 g( y)

and to rotate

about the y-axis (see Figure 7). Reasoning similar to Theorem 1 gives the follo wing

result for the volume of the solid that is obtained when an arc of the curve x 5 g( y)

is rotated about the y-axis.

THEOREM 2

(Method of Disks: Rotation About the y-axis) Suppose that g(y)

is a nonnegative continuous function on the interval c # y # d. Let R denote the

region of the xy-plane that is bounded by the graph of x 5 g(y), the y -axis, and

the horizontal lines y 5 c and y 5 d. Then the volume V of the solid obtained by

rotating R about the y-axis is given by

V 5 π

gðyÞ

dy:

⁄ EX

AMPLE 3 Calculate the volume enclosed when the graph of y 5 x

2 # x # 4, is rotated about the y-axis.

Solution Refer

to Figure 8. Because we are rotating about the y-axis, we want to

use Theorem 2. Therefore we express x as a function of y:

x 5 gðy Þ5 y

1=3

y  x

m Figure 6

x  g(y)

m Figure 7 The planar region R and the solid that R

generates when rotated about the y-axis

13

(2, 8)

(4, 64)

y  x

x  g(y)

 y

1/3

m Figure 8

7.1 Volumes 541

Notice that x 5 2 corresponds to y 5 8, and x 5 4 corresponds to y 5 64. Then,

according to Theorem 2, the desired volume is

V 5 π

ðy

1=3

dy 5

πy

5=3



y564

y58



5=3

2 8

5=3



πð4

2 2

Þ5

2976

π: ¥

The Method of

Washers

Sometimes we want to generate a solid of revolution by rotating the region between

two graphs. Here is an example.

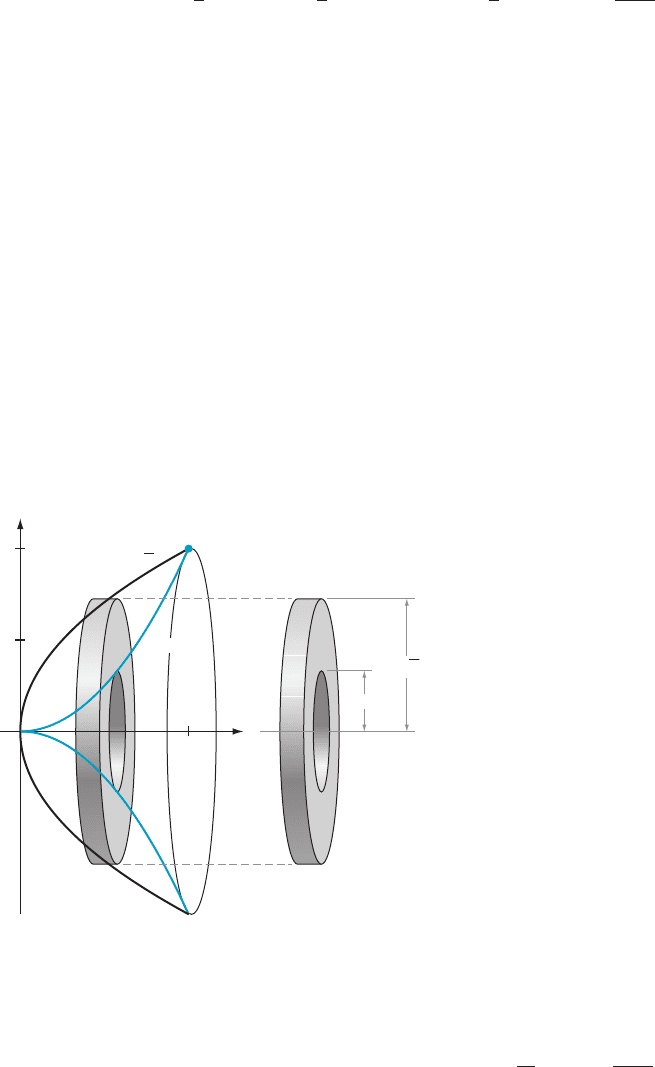
⁄ EX

AMPLE 4 Let D be the region of the xy-plane that is bounded above by

y 5 8

ﬃﬃﬃ

and below by y 5 x

. Calculate the volume of the solid of revolution that is

generated when D is rotated about the x-axis.

Solution When

we decompose this solid of revolution into thin slices, we obtain

pieces that are approximately was hers, not disks (Figure 9). To approximate the

solid, we use washers that correspond to values of x from x 5 0tox 5 4—these

values are found by solving the equation 8

ﬃﬃﬃ

5 x

. The outer radius of the washer

located at x is 8

ﬃﬃﬃ

while the inner radius is x

(see Figure 9). The volume

contribution of this washer is obtained by multiplying the area between the circles

by the thickness of the washer:



πð8

ﬃﬃ

ﬃ

2 πðx



 Δx:

Therefore the volume of the solid is



ð8

ﬃﬃﬃ

2 ðx



dx 5 π

ð64x 2 x

Þdx 5 π



32x





x54

x50

1536

π: ¥

(4, 16)

y  x

y 



m Figure 9

542 Chapter

7 Applications of the Integral

INSIGHT

Notice that it would have been an error in Example 4 to use Theorem 1

with the function f ðxÞ5 8

ﬃﬃﬃ

2 x

. This is because we ﬁnd the area between two

circles by subtracting the area inside the smaller circle from the area inside the larger;

we do not do it by subtracting the radii and squaring the difference.

The reasoning of Example 4 may be used to derive the following theorem.

THEOREM 3

(Method of Washers) Suppose that U and L are nonnegative,

continuous functions on the interval [a, b] with L(x) # U(x)foreachx in this

interval. Let R denote the region of the xy-plane that is bounded above by the

graph of U, below by the graph of L, and on the sides by the vertical lines x 5 a

and x 5 b. Then the volume V of the solid obtained by rotating R about the x-axis

is given by

V 5 π



UðxÞ

2 LðxÞ



dx: ð7:1:6Þ

INSIGHT

Equation (7.1.6) may be written as

V 5 π

UðxÞ

dx 2 π

LðxÞ

dx:

This formula is to be expected because we can obtain the solid of Theorem 3 by ﬁrst

rotating the region under the graph of y 5 U(x) and then removing the solid that is

obtained by rotating the region under the graph of y 5 L(x).

⁄ EXAMPLE 5 Let R be the region of the xy-plane that is bounded above by

y 5 e

,0# x # 1 and below by y 5

ﬃﬃﬃ

; 0 # x # 1. Calculate the volume of the

solid of revolution that is generated when R is rotated about the x-axis.

Solution The

plots of U(x) 5 e

,0# x # 1 and y 5 LðxÞ5

ﬃﬃﬃ

are shown in

Figure 10. To the right of these plots are the surfaces they generate when rotated

about the x-axis. According to Theorem 3, the volume V of the solid bounded by

these surfaces is given by

V 5 π



Uð x Þ

2 LðxÞ



dx 5 π



2 xe



5 π







x51

x50

5 π





2 π





5 π

2 1

: ¥

y  e

y 

x e



m Figure 10

7.1 Volumes 543

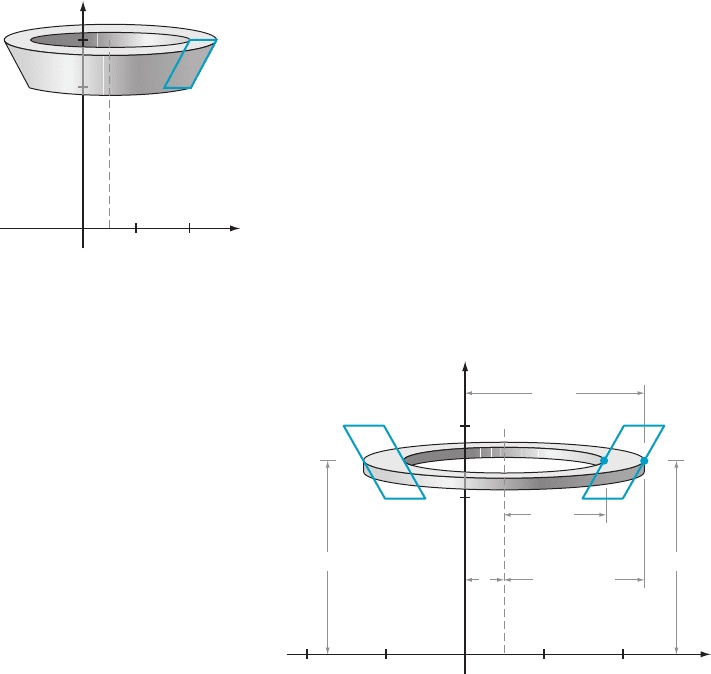
Rotation about a Line

that Is Not a

Coordinate Axis

With only a small modiﬁcation, the analysis leading to Theorems 1 and 2 can be

applied to calculate the volume of a solid of revolution about a line that is parallel

to (but not equal to) one of the coordinate axes. Here is an example.

⁄ EX

AMPLE 6 Rotate the parallelogram bounded by y 5 3, y 5 4, y 5 x, and

y 5 x 2 1 about the line x 5 1, an d ﬁnd the resulting volume V.

Solution The

parallelogram and solid of revolution are illustrated in Figure 11. We

approximate the solid by a union of washers corresponding to values of y between 3

and 4. A typical washer at height y is shown in Figure 12. Because y will be the

variable of integration, we must express the volume of this was her in terms of y.

Refer to Figure 12, noting that the distance of the outer edge of the washer to the

y-axis is the x-coordinate of point P. Because point P is on the line y 5 x 2 1, that

coordinate, expressed in terms of y,isy 1 1. From this, we must subtract 1 to ﬁnd

the dist ance of P to the axis of rotation x 5 1. We conclude that the outer radius of

the washer is (y 1 1) 2 1, or y. Similarly, the inner radius of the washer is 1 unit less

than the x-coordinate of point Q. Expressed in terms of y, the inner radius is y 2 1.

The volume contribution of this washer is therefore



πy

2 πðy 2 1Þ



 Δy:

As before, we su m these volumes and let Δy tend to 0. It follows that

V 5



πy

2 πðy 2 1Þ



dy 5 π



2 ðy

2 2y 1 1Þ



5 π

ð2y 2 1 Þdy 5 πðy

2 yÞ



y54

y53

5 πð16 2 4Þ2 πð9 2 3Þ5 6π: ¥

Now that we have seen severa l instances of calculating volume by the method

slicing, it is a good idea to summarize the basic steps that constitute the method .

y  x

y  x  1

x  1

m Figure 11

x  y

x  y  1

y

(y  1)  1

y  1

y  1

x  1

4

2

m Figure 12 Washer at height y

544 Chapter 7 Applications of the Integral