Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

them, we solve the equation 2x 2 6x

1/2

523. We rewrite this as 2x 1 3 5 6x

1/2

.Ifwe

square each side, then we obtain the quadratic equation (2x 1 3)

5 36x or

2 24x 1 9 5 0. According to the Quadratic Formula, the roots are

3 2 3

ﬃﬃﬃ

=2  0:40192 and 3 1 3

ﬃﬃﬃ

=2  5:59808. As expected, both roots are in

the interval [0, 9].

Random Variables Many important variables assume their values in a “random” manner. For example,

a company may be able to say quite a bit in general abo ut the longevity of the

computer hard drives it produces. The manufacturer cannot, however, say anything

deﬁnite about the lifetime X of the particular hard drive in your computer. We say

that X is a random variable. Similarly, a paleontologist may know what range of

values the heights of velociraptors lie in. What cannot be speciﬁed for certain is the

height of the next specimen to be discovered: It is a random variable.

The Theory of Probability is largely concerned with the analysis of random

variables. The ﬁeld of Statistics uses probability theory to make estimates and

inferences about random variables based on observed values. In this subsection,

you will learn how calculus plays a role in determining the average value of a

random variable.

Suppose that X is a random variable whose values lie in an interval I 5 [a, b]. In

other words, I is the range of X.If[α, β] is a subinterval of I,thenwewrite

P(α # X # β) to denote the probability that the random variable X takes on a value

in the subinterval [α, β]. Just as in everyday informal language, a probability in

mathematics is a number between 0 and 1. For example, we have P(a # X # b) 5 1

because it is certain, according to our assumptions, that X takes a value in this range.

DEFINITION

Suppose that X is a random variable all of whose values lie in an

interval I. If there is a nonnegative function f such that

Pðα # X # βÞ5

f ðxÞdx ð7:3:3Þ

for every subinterval [α, β]ofI, then we say that f is a probability density

function of X. The abbreviation p.d.f. is commonly used. Sometimes the nota-

tion f

is used to emphasize the association between f and X.

⁄ EX

AMPLE 6 In a large class, the grades on a particular exam are all

between 38 and 98. Let X denote the score of a randomly selected student in the

class. Suppose that the probability density function f for X is given by f (x) 5

(136x 2 3724 2 x

)/36000, 38 # x # 98. What is the probability that the grade on a

randomly selected exam is between 72 and 82?

Solution Using

formula (7.3.3), we obtain the probability of a random variable X

assuming a value in [α, β] by integrating the probability density function of X over

[α, β]. Thus taking α 5 72 and β 5 82 in formula (7.3.3), we have

Pð72 # X # 80Þ5

136x 2 3724 2 x

36000

dx 5

36000



68x

2 3724x 2





152

675

 0:225:

That is, the probability that the indicated grade will be between 72 and 82 is about

0.225.

7.3 The Average Value of a Function 565

As has been discussed, if f is a probability density function of a random variable

X whose values all lie in I 5 [a, b], then

f ðxÞdx 5 1. The co nverse to this

observation is also known: If f is any continuous, nonnegative function such that

f ðxÞdx 5 1, then there is a random variable X that has range I and probability

density function f.

⁄ EX

AMPLE 7 Suppose that g(x) 5 1/x

. For what number c is f (x) 5 c g(x)

a probability density function for a random variable whose values all lie in the

interval [1, 3]?

Solution We

calculate

gðxÞdx 5

dx 5











Therefore

f ðxÞdx 5

cgðxÞdx 5 c

gðxÞdx 5

For f to be a probabili ty density function of a random variable with range [1, 3], it is

necessary and sufﬁcient that

f ðxÞdx 5 1. We therefore set 2c/3 5 1 and ﬁnd that

c 5 3/2. Thus f (x) 5 3/(2x

) is a probability density function on [1, 3]. ¥

In many applications, the range of a random variable is an inﬁnite interval of

the form [a,N)or(2N,N). The next example illustrates this idea with an important

type of random vari able known as a waiting time.

⁄ EX

AMPLE 8 Suppose that f ðxÞ5

20000

2x=20000

is the probability density

function of the time to failure X, measured in hours, of an electronic component

that has been placed into service. Verify that f is a probability density function on

the interval [0,N), and calculate the probability that the component will fail within

its ﬁrst 10,000 hours.

Solution Because f is

nonnegative and satisﬁes

20000

2x=20000

dx 5

20000

lim

N-N

2x=20000

20000

lim

N-N



220000 exp



20000







5 lim

N-N



1 2 exp



20000



5 1;

we conclude that it is a probability density function. The probability that the

component will fail within its ﬁrst 10,000 hours is

Pð0 # X # 10000Þ5

10000

20000

2x=20000

dx 52e

2x=20000



x510000

x50

5 1 2 e

21=2

 0:3935: ¥

566 Chapter 7 Applications of the Integral

Average Values in

Probability Theory

Suppose that X is a random variable with range I 5 [a, b] and probability density

function f. Our goal is to determine the average value μ of X. Notice that we cannot

simply use our previous formula and integrate X because we do not have a

deterministic formu la for X. We can calculate the average value f

avg

of f, but this

quantity is not the average value μ of X.

To calculate μ, we again rely on a discrete model. If we made a large number N

of observations X

,...,X

of X, then we would expect

μ 

1 X

1 :::1 X

ð7:3:4Þ

to be a good approximation. Form a partition a 5 x

, x

, ..., x

5 b of the

interval I into M subintervals of equal length Δx. For each j from 1 to M,we

approximate the contribution of the terms in the numerator of formula (7.3.4) that

lie in the j

subinterval I

5 [x

j21

, x

]. First we estimate the number of these

observations. To do so, we note that the probability that an observation of x will fall

in I

Pðx

j21

# X # x

Þ5

j21

f ðxÞdx 5 f ðc

ÞΔx

where f (c

) is the average value of f in the subinterval I

. It follows that about

N ( f (c

)Δx) of the observations will lie in I

. Each of these observations will be

between x

j21

and x

.Becausec

is in this small interval, we may use c

as a repre-

sentative value of the observations in I

. The contribution of the terms in I

is therefore

about c

(N f (c

) Δx). By grouping the summands of X

1 X

1 ...1 X

according

to the subintervals in which they lie, we may rewrite our approximation of μ as

μ 

j51





N  f ðc

ÞΔx



j51

 f ðc

ÞΔx:

Because

j51

 f ðc

ÞΔx is a Riemann sum for the integral

xfðxÞdx, we are led

to the following deﬁnit ion.

DEFINITION

If f is the probability density function of a random variable X that

takes values in an interval I 5 [a, b], then the average (or mean) μ of X is deﬁned

to be

μ 5

xfðxÞdx: ð7:3:5Þ

This value is also said to be the expectation of X. Other notations for the

expectation of X are

X and E(X).

⁄ EX

AMPLE 9 Let X denote the fraction of total impurities that are ﬁltered

out in a particular puriﬁcation process. Suppos e that X has probability density

function f (x) 5 20x

(1 2 x) for 0 # x # 1. What is the average of X?

Solution Acco

rding to our deﬁnition, the average is

X 5

x  20x

ð1 2 xÞdx 5

ð20x

2 20x

Þdx 5 20







x51

x50

: ¥

7.3 The Average Value of a Function 567

Population Density

Functions

The idea of a density function arises in many topics outside of probability theory. In

the next section, we will encounter mass densities, which are important in physics

and engineering. We conclude the present section with a discussion of population

densities, which are used for societal planning.

In a simple model for the growth of a city, the municipality’s land mass expands

radially in all directions from the central point of its initial foundation. We

represent the city’s center by the origin in the plane and supp ose that there are no

geographic or economic factors that favor one radial direction over another for

settlement. As a result of this assumption, the num ber of people living in a small

square R of area A is about f (r) A, where f (r) is a proportionality constant

depending on the distance r of the center of R from the origin but not on the

particular location of the center on the circle x

1 y

5 r

(see Figure 4). Let us use

this population density f to calculate the number P(R) of inhabitants living up to a

distance R from the city center.

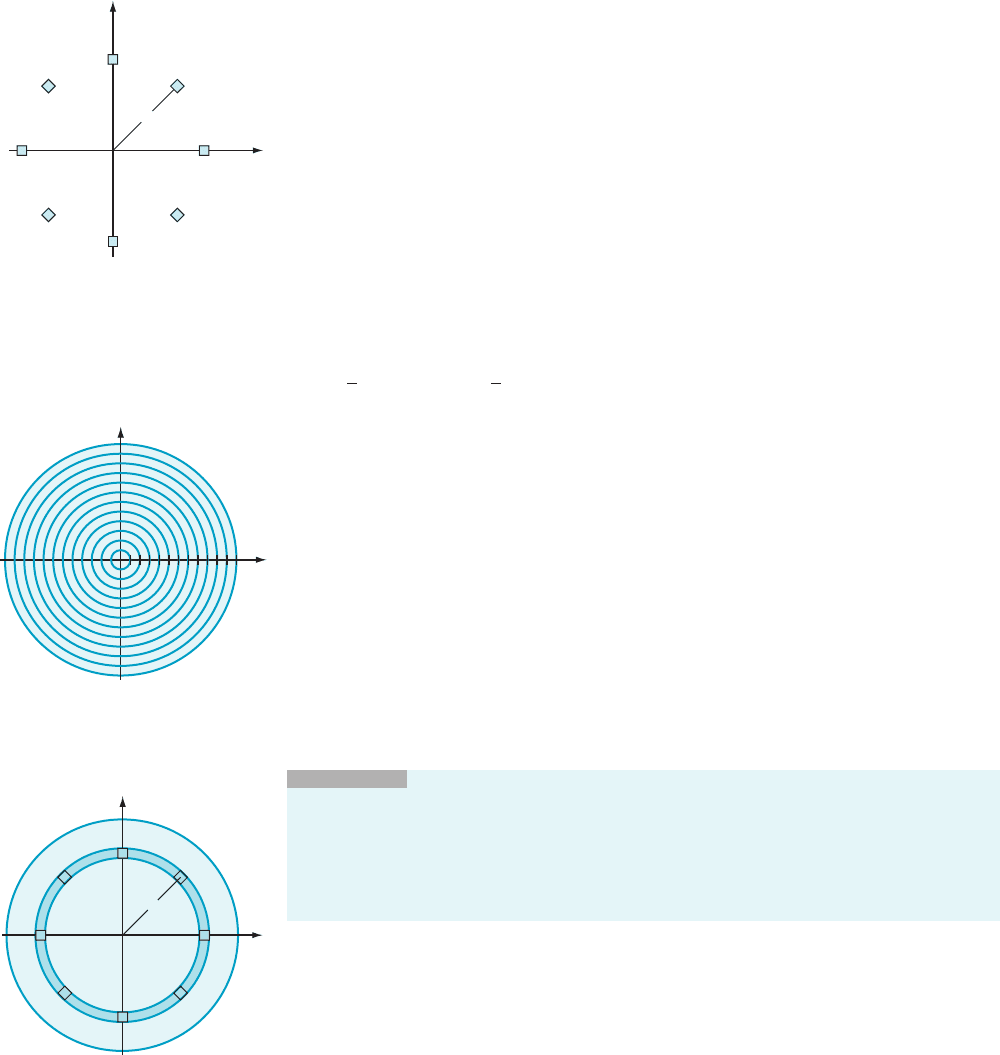
The partition x

5 0, x

5 R/N, x

5 2R/N,...,x

N21

5 (N 2 1) R/N, x

5 R divides

the interval [0, R] of the x-axis into N subintervals of equal length Δx 5 R/N. We can

use this partition of [0,R] to divide the disk of radius R centered at the origin into N

concentric rings, as shown in Figure 5. Let s

be the midpoint of the j

subinterval

j21

, x

]of[0,R]. Then, for 2 # j # N, the area A

of the j

ring is eq ual to



Δx



2 π



Δx



; or 2π s

Δx. We can also use this expression as an

approximation to the area A

of the ﬁrst “ring,” which is actually a disk. In Figure 6,

several squares are drawn inside the j

ring. Each has side length Δx and a center that

is a distance s

from the origin. If we continue to ﬁll in the ring with such squares until

the ring is approximately covered, then each square in the covering has area A 5

(Δx)

and approximately f (s

) A inhabitants. If we sum the contributions of these

squares to the total population P

of the j

ring, then, afte r factoring the common

coefﬁcient f (s

), we obtain P

 f ðs

Þ3 A

,orP

 2π s

f ðs

ÞΔx. Because the total

population P(R) in the disc of radius R centered at the origin is equal to P

1 P

...1 P

, we see that PðRÞ

j51

2π s

f ðs

ÞΔx. Observe that this expression is a

Riemann sum for the integral

2π xfðxÞdx. Thus on letting N tend to inﬁnity, we

obtain

PðRÞ5 2π

xfðxÞdx: ð7:3:6Þ

INSIGHT

Despite the apparent similarity between the integrals of formulas (7.3.5)

and (7.3.6), there are signiﬁcant differences that should be noted. The probability density

function of formula (7.3.5) is integrated over the range of the random variable X. The

population density function of formula (7.3.6) is integrated over a subinterval of the

domain of the population function P. Equation (7.3.5) is a formula for the average value

of X. Equation (7.3.6) can be used to calculate all values of P.

⁄ EXAMPLE 10 In 1950, the population density of Tulsa was given by

f (x) 5 28000e

24x/5

, where x represents the distance in miles from the central

business district. About how many people lived within 20 miles of the city center?

Solution Accord

ing to formula (7.3.6), Pð20Þ5 2π

28000 xe

24x=5

dx. Using

formula (6.1.9) with n 5 1 and a 524/5, we have

The population in each shaded square

of area A is about f

(

)

· A

m Figure 4

m Figure 5

j1

m Figure 6

568 Chapter

7 Applications of the Integral

Pð20Þ5 56000 π



24x=5



24x=5



5 56000 π



225 e

216



24x=5







5 56000 π



225 e

216



216



5 56000 

 π ð1 2 17e

216

 274 ; 889: ¥

QUICK QUIZ

1. What is the average of sin(x) over the interval [0, π]?

2. For what c in I 5 [0, 3] is f (c) the average value of f (x) 5 x

on I?

3. Suppose that the probability density of a nonnegative random variable X is

f (x) 5 exp(2x), 0 # x ,N. What is the probability that X # 1?

4. What is the mean of a random variable that has probability density function

f (x) 5 x/2 for 0 # x # 2?

Answers

1. 2/π 2.

ﬃﬃ

ﬃ

3. 1 2 1/e 4. 4/3

EXERCISES

Problems for Practice

c In each of Exercises 1212, calculate the average value of

the given function on the given interval. b

1. f (x) 5 cos(x) I 5 [0, π/2]

2. f (x) 5 x

I 5 [3, 7]

3. f (x) 5 1/xI5 [1, 4]

4. f (x) 5 3x

2 6x 1 1 I 5 [3, 7]

5. f (x) 5 sin(x) I 5 [π/3, π]

6. f (x) 5 1 1 cos(x) I 5 [0, 2π]

7. f (x) 5 (x 2 1)

1/2

I 5 [2, 5]

8. f (x) 5 x

1/2

2 x

1/3

I 5 [0, 64]

9. f (x) 5 60/x

I 5 [1, 3]

10. f (x) 5 e

I 5 [21, 1]

11. f (x) 5 ln(x) I 5 [1, e]

12. f (x) 5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

169 2 x

I 5 [5, 12]

c In each of Exercises 13216, a function f and

an interval

I 5 [a, b] are given. Find a number c in (a, b) for which f (c)is

the average value of f on I. b

13. f (x) 5 1/xI5 [1,

14. f (x) 5 e

I 5 [ln(2), ln(4)]

15. f (x) 5 x

2 10x/3 I 5 [1, 3]

16. f (x) 5 ln(x) I 5 [1, e]

c In each of Exercises 17222, the probability density function

f of

a random variable X with range I 5 [a, b] is given. Calculate

P(α # X # β) for the given subinterval J 5 [α, β]ofI. b

17. f (x) 5 3x

/8 I 5 [0, 2] J 5 [1, 2]

18. f (x) 5 12x

(1 2 x) I 5 [0, 1] J 5 [0, 1/2]

19. f (x) 5 sin(x)/2 I 5 [0, π] J 5 [π/4, π/2]

20. f (x) 5 3(1 1 x)/(8

ﬃﬃﬃ

) I 5 [0, 1] J 5 [1/4, 1/2]

21. f (x) 5 e

12x

/(e 2 1) I 5 [0, 1] J 5 [0, 1/2]

22. f (x) 5 ln(x) I 5 [1, e] J 5 [3/2, 2]

c In each of Exercises 23228, a function g and

an interval I

are speciﬁed. The function g is nonnegative on I. Find a

number c such that f (x) 5 cg(x) is a probability density

function on I. b

23. g(x) 5 sec

(x) I 5 [0, π/3]

24. g(x) 5 1/x

I 5 [1, 2]

25. g(x) 5 9 2 x

I 5 [21, 3]

26. g(x) 5 e

I 5 [0, 1]

27. g(x) 5 e

22x

I 5 [0,N]

28. g(x) 5 1/(1 1 x

) I 5 (2N,N)

c In each of Exercises 29236, calculate the mean of the

random

variable whose probability density function is

given. b

7.3 The Average Value of a Function 569

29. f (x) 5 3x

I 5 [0, 1]

30. f (x) 5 2(1 2 x) I 5 [0, 1]

31. f (x) 5 1/(3

ﬃﬃﬃ

) I 5 [1/4, 4]

32. f (x) 5 6x(1 2 x) I 5 [0, 1]

33. f (x) 5 x

/3 I 5 [21, 2]

34. f (x) 5 3/(π(1 1 x

) I 5 [0,

ﬃﬃﬃ



35. f ðxÞ5

2lnðxÞ

I 5 ½1; e

36. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

I 5 ½0; 1

37. In 1980, the population density for the central core of

Houston, a disk with a 6-mile radius, was f (x) 5 5860

exp(20.148x). What was the population of that part of

Houston?

38. In 1960, the population density for the central core of

Denver, a 72 mi

disk, was f (x) 5 14000 exp(2x/4). What

was the population of that part of Denver?

Further Theory and Practice

39. In 1950, the population density in the central core of

Akron, a disk with a 4-mile radius, was f ( x) 5 13000

exp(20.38x). In 1970, the population density was f (x) 5

10000 exp(20.29x). Did the population in that part of

Akron increase or decrease? By about how many people?

40. If a city’s population density is given by f (x) 5

A/(B 1 Cx) for positive constants A, B, and C, then how

many people live farther than a distance a from the center

but closer than a distance b from the center?

41. A patient with a fever has temperature at time t (mea-

sured in hours) given by

TðtÞ5 99: 6 2 t 1 0:8t

degrees;

where temperature is measured in degrees Fahrenheit.

Find the patient’s average temperature as t ranges from 0

to 3.

42. The temperature distribution on a uniform rod of length 4

meters is T(s) 5 18 1 6s

2 2s 1

ﬃﬃ

,0# s # 4. What is the

average temperature of the rod?

c In each of Exercises 43252 calculate the average of the

given

expression over the given interval. b

43. x exp(x

)0# x # 2

44. x sin(x)0# x # π

45. 3π cos(x)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 sinðxÞ

0 # x # π/2

46. sin

(x)0# x # π

47. cos

(x) sin

(x)0# x # π

48. sin

(2x)0# x # π/2

49. 4x ln(x)1# x # e

50. ln(x)/x 1 # x # e

51.

5x 1 2

1 x

1 # x # 3

52. 24x arcsin(x)0# x # 1/2

53. For what value of c is 21/2 the average value of (x 2 c)

sin(x) over the interval [0, π/3]?

54. Is the average value of cos(x) for 0 # x # π/4 equal to the

reciprocal of the average value of 1/cos(x) over the same

x-interval?

55. The outdoor temperature in a certain town is given by

TðtÞ5 40 2 ðt 2 45Þ

=200

for t ranging from 0 to 72 hours. Use the deﬁnition of

degree days given in Example 3 to calculate the degree

days for each of the three successive 24-hour periods. If

fuel costs a certain homeowner $0.30 per degree day, what

does it cost her to heat her house during these three days?

56. The temperature of an aluminum rod at point x is given by

TðxÞ5

2 t

1 32; 0 # t # 2

36 2 2t 1 t

; 2 , t # 8:



Find the average temperature of the rod.

57. For what a, 0 # a # π, does the function f (x) 5 sin(x) 2

cos(x) have the greatest average over the interval

[a, a 1 π] of length π?

58. Given c . 0, for what value b,0, b , c, is exp(b) equal to

the average of exp(x) for 0 # x # c.

c In each of Exercises 59264, a nonnegative continuous

function g and

an interval I are speciﬁed. The function g is

nonnegative on I. Find a positive real number c for which

f (x) 5 cg(x) is a probability density function. b

59. g(x) 5 x ln(x)

[1, e]

60. x

(1 2 x)

[0, 1]

61. x

(1 2 x

)

21/2

[0, 1]

62. (9 1 x

)

21/2

[0, 4]

63. arcsin(x) [0, 1]

64. x(1 2 x)

21/2

[0, 1]

c In each of Exercises 65274 calculate the expectation of a

random

variable whose probability density function is

given. b

65.

sinðxÞ 0 # x # π

66.

2π



1 1 cosðxÞ



0 # x # 2π

67.

ðx

1 1Þ

0 # x # 1

68. e

12x

=ðe 2 1Þ 0 # x # 1

69.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 2 x

0 # x # 4

70.

4arctanðxÞ

π 2 2lnð2Þ

0 # x # 1

71. 2e

22x

0 # x ,N

72.

ﬃﬃﬃ

expð2x

Þ 0 # x , N

570 Chapter 7 Applications of the Integral

73.

πð1 1 x

0 # x , N

74.

ð1 1 x

0 # x , N

c If P(X # m) 5 P(X $ m) 5 1/2,

then we say that m is the

median of a random variable X . In each of Exercises 75278,

calculate

the median of a random variable whose probability

density function f is given. b

75. f (x) 5 cos(x)0# x # π/2

76. f (x) 5 3x

/26 1 # x # 3

77. f (x) 5 e

12x

/(e 2 1) 0 # x # 1

78. f (x) 5 4x(1 2 x

)0# x # 1

79. Let p be a positive constant. Let X be a random variable

with range [0, 1] and probability density function f (x) 5

( p 1 1)x

,0# x # 1. Show that X 6¼ f

avg

. (In general, the

average of a random variable is not equal to the average

of its probability density function.)

80. Let p be a positive constant. Suppose that X is a random

variable with probability density function f (x) 5 ( p 1 1)

for 0 # x # 1.

a. Show that g(u) 5 1 1 u 2 2

satisﬁes 0 , g

(u)

for 0 , u , log

(1/ln(2))  0.529, and g

(u) , 0 for

log

(1/ln(2)) , u.

b. Use the values g(0) 5 g(1) 5 0 together with the

inequalities of part a to deduce that 0 , g(u) for

0 , u , 1.

c. By setting u 5 1/(p 1 1) in the inequality 0 , g(u),

deduce that

1=ðp 1 1Þ

p 1 2

p 1 1

d. Show that the mean of X is not equal to the median

of X. (In general, the mean of a random variable is not

equal to its median.)

81. Suppose that f is a continuous positive function on the

unbounded interval [a,N). Is it appropriate to make the

deﬁnition

avg

5 lim

N-N

N 2 a

f ðxÞdx?

Discuss why or why not.

82. Let λ be a positive constant. Show that f ðxÞ5

λexpð2λxÞ; 0 # x , N is a probability density function.

Show that the mean of a random variable with probability

density function f is 1/λ.

c If μ is

any real number, and σ is any positive real number,

then

μ;σ

ðxÞ5

ﬃﬃﬃﬃﬃﬃ

2π

exp



x 2 μ



; 2N , x , N

is a probability density function. Exercises 83 and 84 are

concerned

with a random variable X that has probability

density function f

μ,σ

. Such an X is called a normal or Gaussian

random variable. If μ 5 0 and σ 5 1, we use the term standard

normal. The parameter σ is called the standard deviation of

X. b

83. Show

that μ is the mean of a random variable that has

probability density function f

μ, σ

84. Suppose that X is a random variable that has probability

density function f

μ,σ

. Prove that

Pðμ 2 k σ # X # μ 1 k σÞ5

ﬃﬃﬃﬃﬃﬃ

2π

exp





dx:

Calculator/Computer Exercises

c In each of Exercises 85288,afunctionf is given. Let A

(c)

denote the average value of f over the interval [c 2 1/4, c 1 1/4].

Plot y 5 f (x)andy 5 A

(x)for 21 # x # 1. The resulting plot

will illustrate the gain in smoothness that results from

averaging. b

85. f (x) 5 |x|

86. f (x) 5

ﬃﬃﬃﬃﬃ

jxj

87. f ðxÞ5

fx , 0

1if0# x



88. f ðxÞ5

if x , 0

1 x if 0 # x



c In each of Exercises 89292, a function f and

an interval I

are given. Calculate the average f

avg

of f over I, and ﬁnd a

value c in I such that f (c) 5 f

avg

. State your answers to three

decimal places. b

89. f ðxÞ5

ﬃﬃ

ﬃ

expð2xÞ I 5 ½0; 4

90. f ðxÞ5 sinðπðx

2 x

ÞÞ I 5 ½0; 1

91. f ðxÞ5 x=ð16 1 x

Þ I 5 ½2; 4

92. f ðxÞ5

lnðxÞ

1 1 x

I 5 ½1; e

93. What is the probability that the value of a normal random

variable is within one standard deviation of the mean?

Refer to Exercise 84.

94. What is the probability that the value of a normal random

variable is within two standard deviations of the mean?

Refer to Exercise 84.

7.3 The Average Value of a Function 571

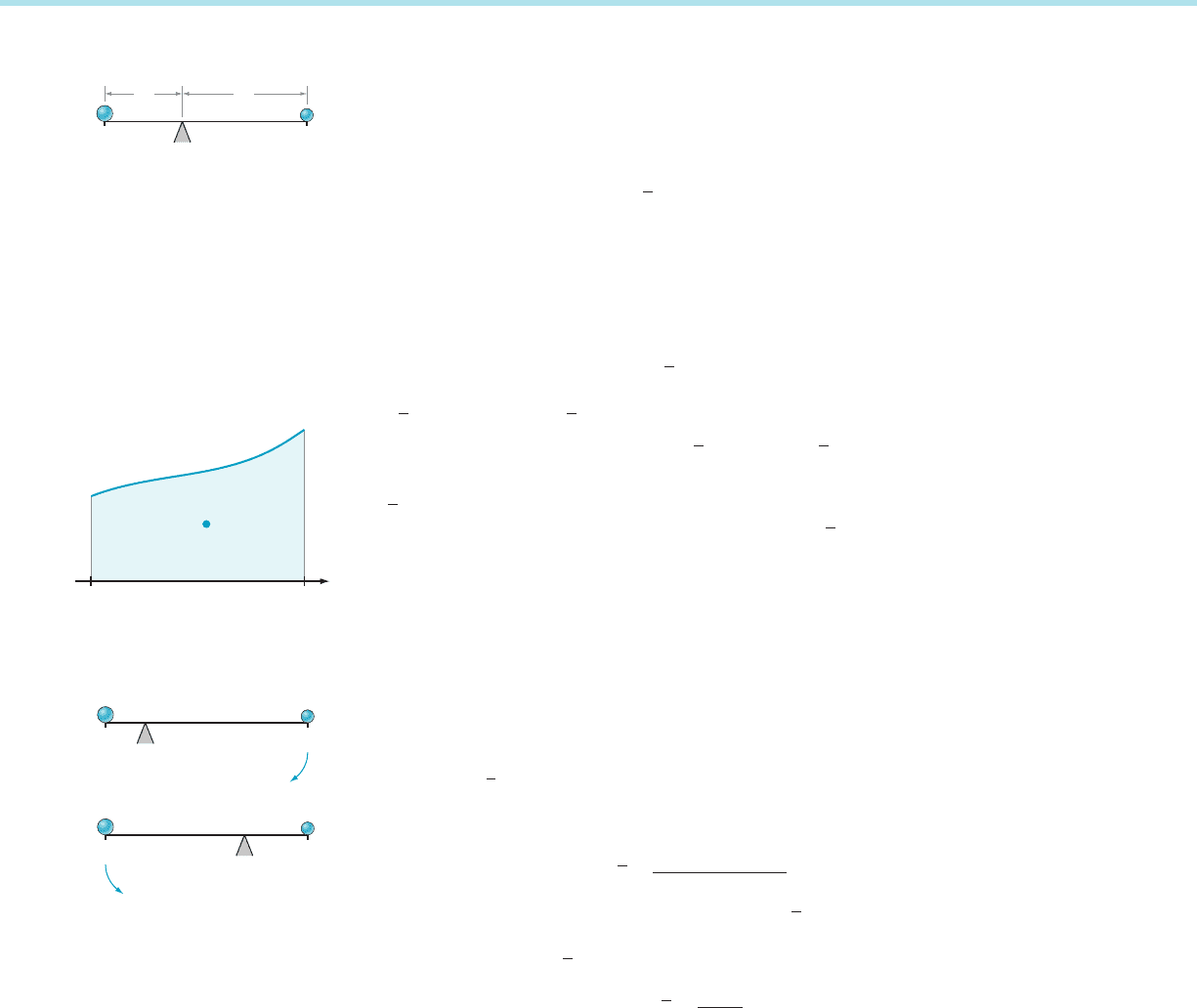
7.4 Center of Mass

When two children of different masses m

and m

play on a seesaw, they ﬁnd that

they can balance the seesaw if they position themselves appropriately. Let us set up

a simple model of the seesaw. Suppose that two point masses m

and m

are

situated at endpoints of an interval [x

, x

] on the x-axis, as in Figure 1. If a fulcrum

could be positioned unde rneath the axis, and if the interval could pivot about the

fulcrum, then at what coordinate

x should we place the fulcrum so as to achieve a

balance? According to the lever law of physics, the masses are in balance if and

only if the distances d

and d

to the fulcrum satisfy the equation m

5 m

.In

this section, we will use this simple principle, together with calculus, to determine

the balancing point of a planar region such as the one shown in Figure 2.

Moments (Two Point

Systems)

Before turning our attention to planar ﬁgures, it is useful to study the seesaw of

Figure 1 in greater detail. The point

x is said to be the center of mass of the system.

We may rewrite the equation m

5 m

in terms of the center of mass as follows:

(x 2 x

) 5 m

(x

2 x)or

0 5 m

ðx

2 xÞ1 m

ðx

2 xÞð7:4:1Þ

The right side of equation (7.4.1) is said to be the moment about the vertical axis

x 5

x. The lever law as expressed by equation (7.4.1) tells us that our system will

balance if and only if the moment about the axis x 5

x is zero. In general, if we

position the fulcrum at any point x 5 c, then we deﬁne the moment M

x5c

about the

axis x 5 c to be the expression

x5c

5 m

ðx

2 cÞ1 m

ðx

2 cÞ: ð 7 :4:2Þ

The moment about the y-axis,

x50

5 m

 x

1 m

 x

; ð7:4:3Þ

is an important special case. Moments may be positive, negative, or 0. In the ﬁrst

two cases, the axis will swing about the fulcrum as shown in Figure 3.

Equations (7.4.1) and (7.4.2) provide us with a method of determining the

center of mass

x of our two point system; we set M

x5c

5 0 in equation (7.4.2) and

solve for c. Thus 0 5 m

ðx

2 cÞ1 m

ðx

2 cÞ; or m

c 1 m

c 5 m

 x

; or c 5 ðm

 x

1 m

 x

Þ=ðm

1 m

Þ. Thus

x 5

 x

1 m

 x

1 m

Notice that the numerator of this expression for

x is the right side of equation

(7.4.3). If we let M 5 m

1 m

denote the total mass of the system, then we can

rewrite our formula for

x in the form

x 5

x50

Moments Now let’s consider the region R shown in Figure 4. We suppose that the region has

uniform mass density δ. By this we mean that the mass of any subset of R is δ times

the area of the subset. Imagine the xy-plane to be horizontal and position a fulcrum

underneath the axis x 5 c (Figure 5). What must c be so that region R does not

swing to one side or the other? To answer this question, we form a partition

Fulcrum at

x  x

–

m Figure 1

y  f(x)

m Figure 2 The shaded region

balances at point P.

xa

 0

xa

 0

Fulcrum at

x  a

Fulcrum at

x  a

m Figure 3

572 Chapter

7 Applications of the Integral

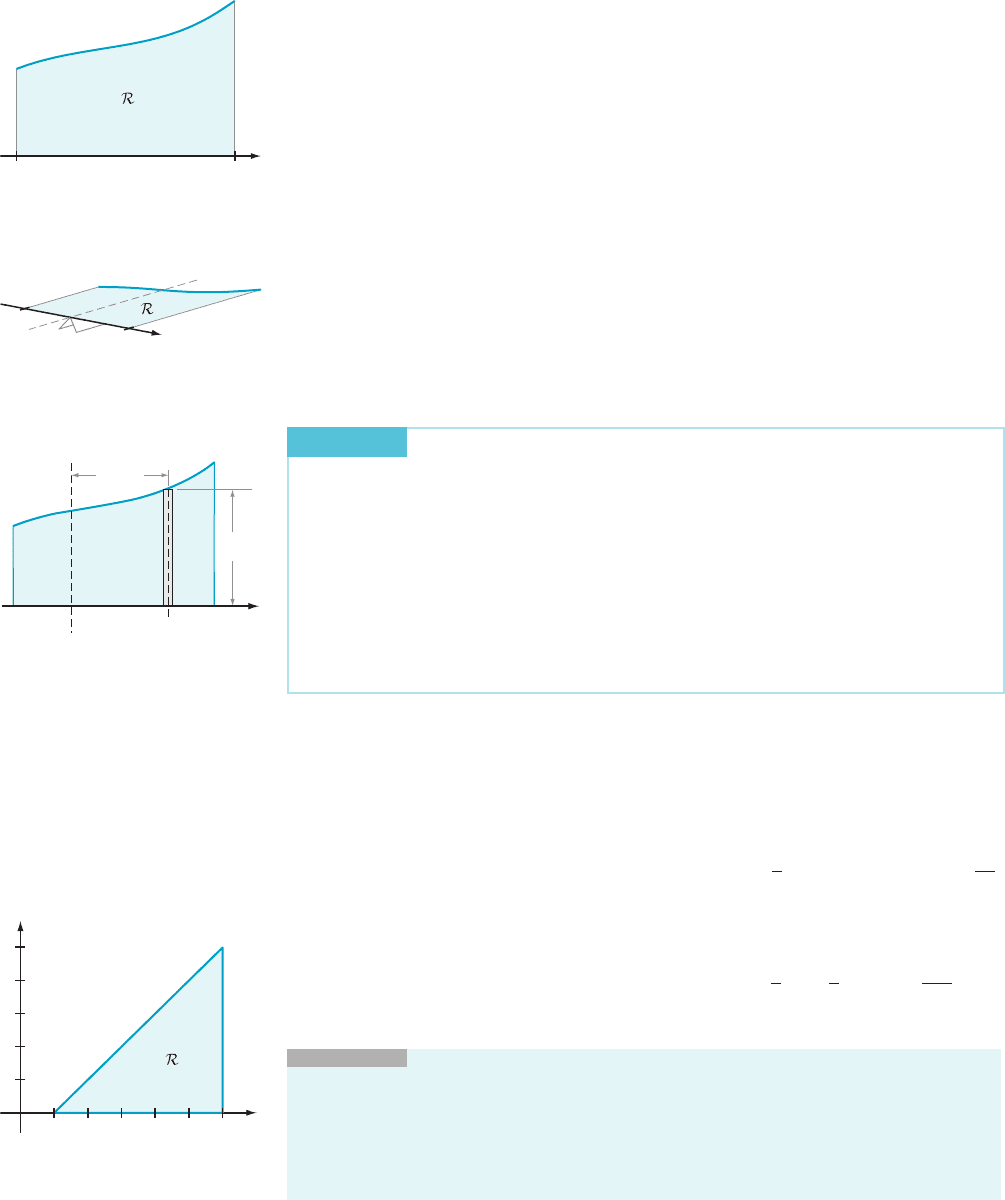
a 5 x

, x

, ..., x

5 b of the interval [a, b]. Let Δx denote the common length of

the subintervals, and let s

be the midpoint of the j

subinterval I

. We divide region R

into the N pieces that lie over the subintervals I

, I

,...,I

. The piece that lies over I

is approx imately a rectangle with base Δx and height f (s

)—see Figure 6. The mass of

this piece is theref ore approximately equal to δf (s

)Δx. Notice that, if Δx is small,

then the points in this j

piece of R are all approximately a (signed) distance (s

2 c)

from the axis x 5 c. The contribution that this piece makes to the tendency of R to

pivot about x 5 c is therefore ab out (s

2c) δf (s

)Δx. The total tendency (or moment)

x5c

to pivot about the axis x 5 c is approximately

j51

ðs

2 cÞδf ðs

ÞΔx: ð7:4:4Þ

As N increases, Δx decreases, and exp ression (7.4.4) becomes a better approximation

to the tendency of R to rotate about the line x 5 c. Because expression (7.4.4) is a

Riemann sum for the integral

ðx 2 cÞδf ðxÞdx, we are led to the following

deﬁnition.

DEFINITION

Let c be any real number. Suppose that f is contin uous and

nonnegative on the interval [a, b]. Let R denote the planar region bounded

above by the graph of y 5 f (x), below by the x-axis, and on the sides by the line

segments x 5 a and x 5 b.IfR has a uniform mass density δ, then the moment

x5c

of R about the axis x 5 c is deﬁned by

x5c

ðx 2 cÞδ f ðxÞdx 5 δ

ðx 2 cÞf ðxÞdx:

Notice that the moment M

x5c

is deﬁned even if the number c is not between a

and b.

⁄ EX

AMPLE 1 Let R be the region bounded by y 5 x 2 1, y 5 0, and x 5 6

(as shown in Figure 7). Suppose that R has uniform mass density δ 5 2. Calculate

the moments about the axes x 5 5 and x 5 0.

Solution The

required moments are

x55

5 2

ðx 2 5Þðx 2 1Þdx 5 2

ðx

2 6x 1 5Þdx 5 2



2 3x

1 5x





and

x50

5 2

ðx 2 0Þðx 2 1Þdx 5 2

ðx

2 xÞdx 5 2







325

: ¥

INSIGHT

In Example 1, the signs of M

x55

and M

x50

could have been determined

simply by inspecting Figure 7. Imagine a horizontal plate in the shape of R . Our

experience tells us that, if the plate were allowed to pivot about the axis x 5 5, then the

left side would fall. From this, we conclude that M

x55

, 0. (It may be useful to refer back

to Figure 3, which illustrates the analogous behavior of a seesaw.) Similar reasoning leads

to the conclusion that M

x50

must be positive.

y  f(x)

m Figure 4

y  f(x)

x  c

m Figure 5

x  c

y  f(x)

f(s

)

j1

 c

m Figure 6

y  x  1

x  6

123456

m Figure 7

7.4 Center of Mass 573

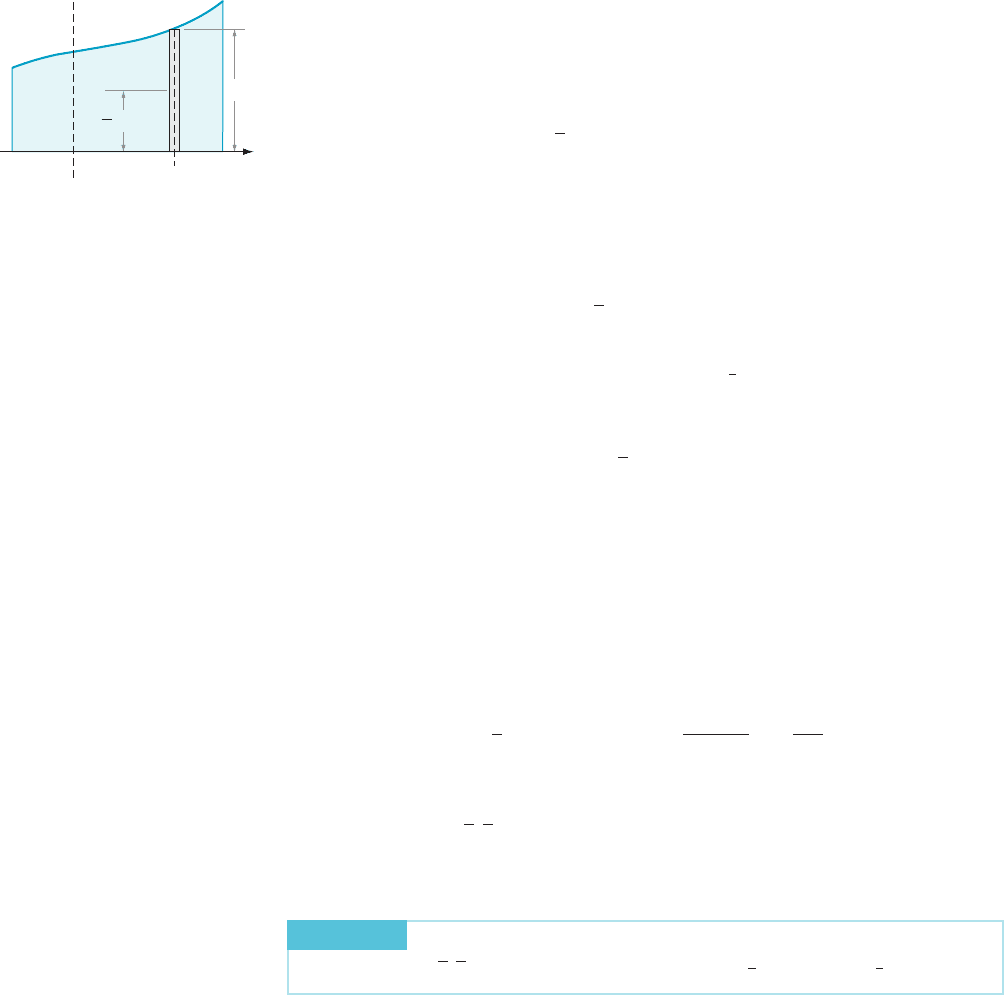
Consider again the region R that is shown in Figure 4. We would like to deﬁne

the moment M

y5d

of R about a horizontal axis y 5 d. Unfortunate ly, we cannot do

so in a way that is analogous to the deﬁnition of moments about vertical axes. The

reason can be seen in Figure 6. The key idea behind the deﬁnition of the moment

x5c

is that, if the rectangle is thin, then the point masses within the rectangle are

nearly equidistant from the vertical axis x 5 c. Clearly that cannot be true for any

horizontal axis.

A thorough solution to the problem of deﬁning M

y5d

requires multivariable

calculus. For now, let us consider only the mom ent M

y50

, the moment about the x-

axis. Glance at Figure 8. The average distance to the x -axis of the points in the

rectangle is f (s

)/2. It therefore seems plausible to use

f ðs

|ﬄﬄ{zﬄﬄ}

Average distance

 δf ðs

ÞΔx

|ﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄ}

Approximate mass

as an approximation of the moment of the rectangle about the x-axis. Then the

resulting approximation to the total moment of R about the x-axis is

j51

f ðs

Þδf ðs

ÞΔx:

Because this is a Riemann sum of the integral

δf ð x Þ

dx, we are led to deﬁne

y50

by the formula

y 5 0

f ðxÞ

dx: ð7:4:5Þ

After we have studied some multivariable calculus, we will have the tools to rig-

orously justify this formula.

⁄ EX

AMPLE 2 Let R be the region bounded by y 5 x 2 1, y 5 0, and x 5 6

(as in Example 1). Suppose that R has uniform mass density δ 5 2. Calculate the

moment M

y50

Solution Accord

ing to formula (7.4.5), the required moment is

y50

ð2Þ

ðx 2 1Þ

dx 5

ðx 2 1Þ



125

: ¥

Center of Mass The center of mass (x, y) of a region R is the point at which the region balances (as

in Figure 2). To ﬁnd the center of mass, we must translate this physical property

into mathematical equations.

DEFINITION

Let R be a region as shown in Figure 4. Then the center of mass of

R is the point (

x, y) whose coordinates satisfy M

x5x

5 0 and M

y5y

5 0.

x  c

y  f(x)

f(s

)

f(s

)

j1

m Figure 8

574 Chapter

7 Applications of the Integral