Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Steps in Calculating Volume by The Method of Slicing

1. Identify the shape of each slice.

2. Identify the independent variable that gives the position of each slice.

3. Write an expression, in terms of the independent variable, which describes the cross-sectional area of each

slice.

4. Identify the interval [a, b] over which the independent variable ranges.

5. With respect to the independent variable of Step 2, integrate the expression for the cross-sectional area from

Step 3 over the interval [a, b] from Step 4.

Now let us do another example in which we explicitly follow these ﬁve steps.

You will notice that, if each step can be completed, then the method of slicing can

be applied even if the slices are neither disks nor washers.

⁄ EX

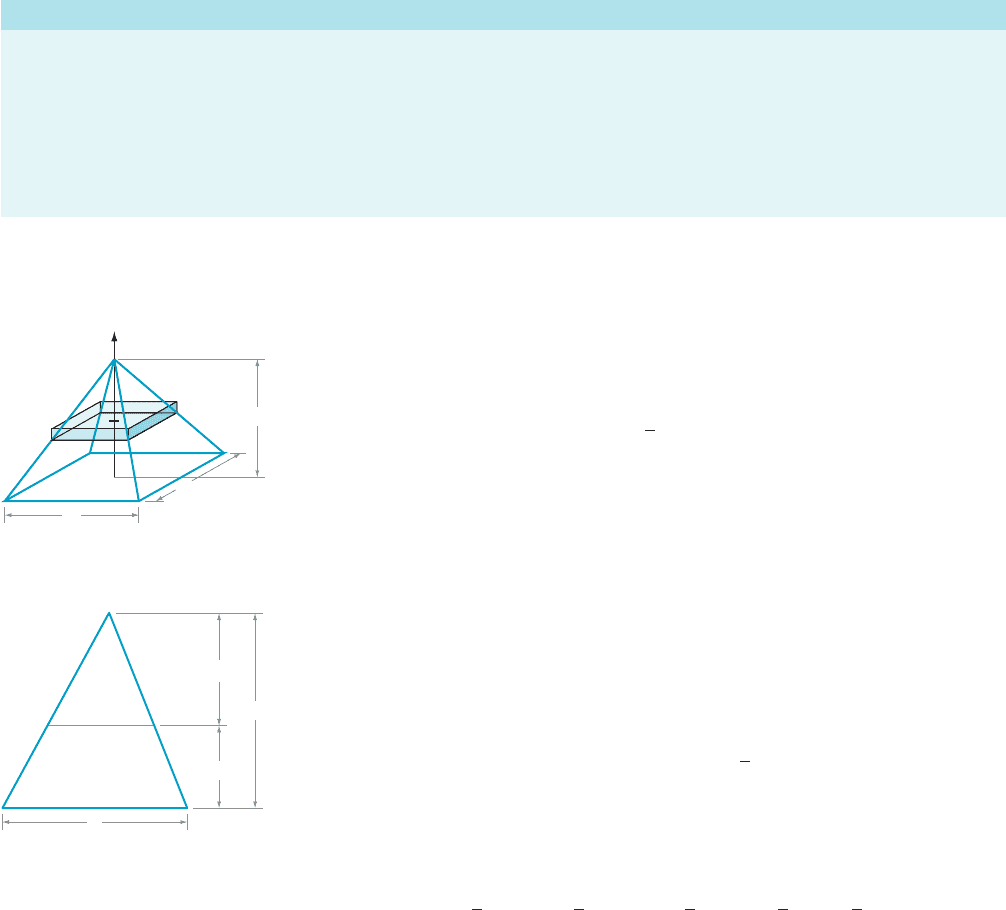
AMPLE 7 (A Solid That Is Not Generated by Rotation) Let V be the

volume of a solid pyramid that has height h and rectangular base of area A. Then,

V 5

Ah:

Verify this formula for a solid pyramid of height 5 if the width and depth of the

base are 2 and 3, respectively.

Solution

1. The cross -section of each slice will be a rectangle—see Figure 13.

Because the slices are perpendicular to the y-axis, each slice is located by its

position on the y-axis. So we make y the independent variable.

3. Let w( y) and d( y) denote the width and depth of the rect angular cross -section

of the slice at height y. A similar triangular argument (see Figure 14) reveals

that w ( y)/2 5 (5 2 y)/5 or w( y) 5 2 (5 2 y)/5 5 2(1 2 y/5). Lik ewise, d( y) 5 3 

(5 2 y)/5 5 3(1 2 y/5). Therefore the cross-sectional area of the slice is

wðyÞdðyÞ5 2  3 



1 2



4. The range of the independent variable y is given by the extreme values of

y: yA[0, 5].

5. The volum e is

6 



1 2



dy 52

6  5 



1 2





y55

y50

6  5 5

A  h: ¥

The Method of

Cylindrical Shells

For certain solids of revolution, the method of disks or washers is either difﬁcult or

not feasible. To handle such cases, we will develop an alternative method for

calculating the volumes of solids of revolution. It is called the method of cylindrical

shells because it uses these pipe-like objects (Figure 15) rather than disks or

washers a s basic building blocks. This new method rests on a simple observation:

The volume of a thin cylindrical shell of radius r, height h, and thickness t is

approximately (2πr) h t. (Imagine cutting straight down the side of the cylindrical

shell and ﬂattening it out. The result is approximately a parallelepiped with side

lengths 2πr, h, and t as shown in Figure 15 .)

m Figure 13

w(y)

5  y

m Figure 14

7.1 Volumes 545

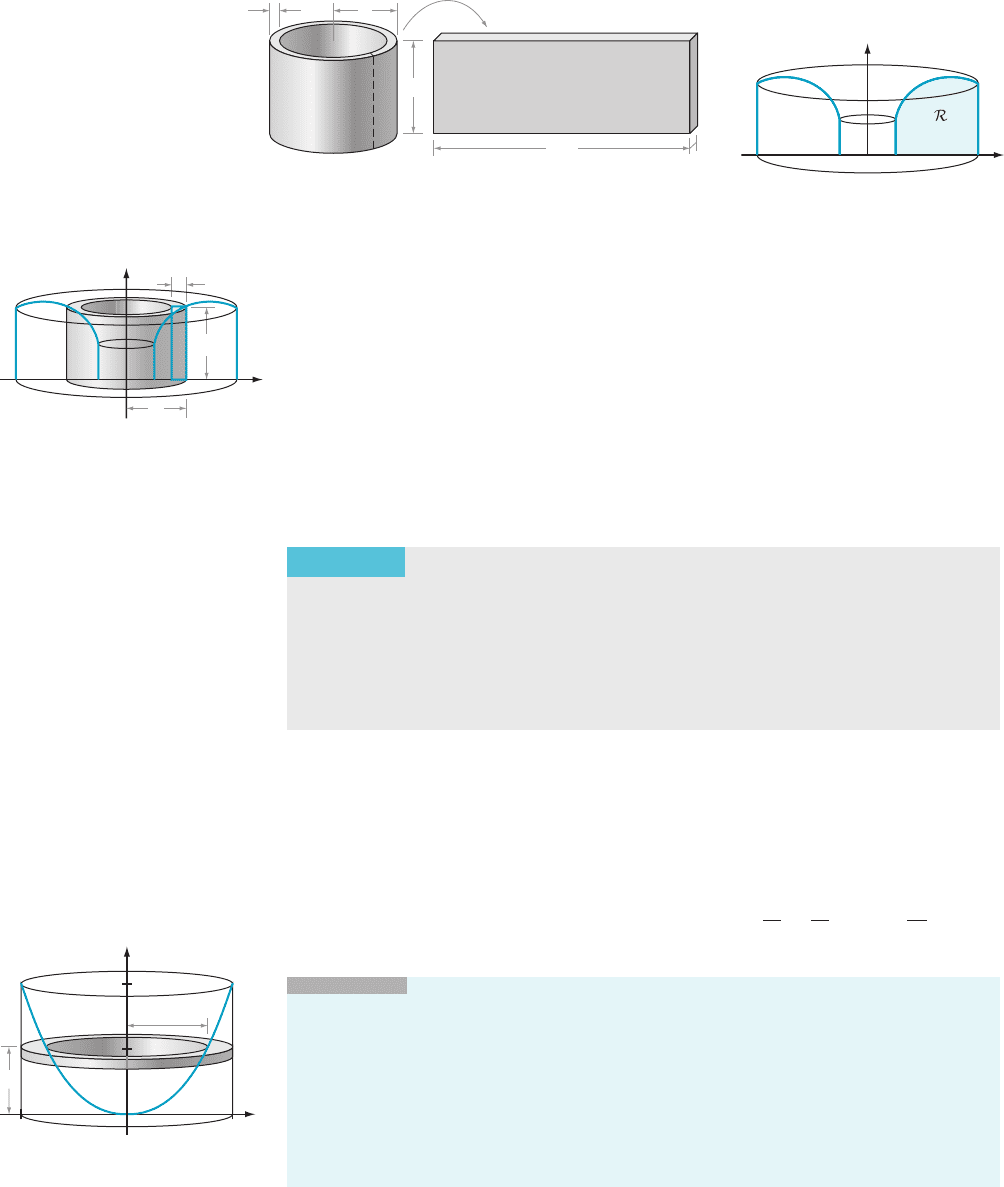
Let f be a nonnegative continuous function on an interval [a, b] of nonne gative

numbers. Consider the planar region R (shaded in Figure 16) that is bounded by

the graph of y 5 f (x ), x 5 a, x 5 b, and the x-axis. We seek the volume V of the solid

of revolution that is generated by rotating R about the y-axis as in Figure 16. To

approximate V, we partition the interval [a, b] into N subintervals of equal width

Δx. Corresponding to each subinterval of the partition, we form a thin rectangle as

in Figure 17. When region R is rotated, the thin rectangle sweeps out a cylindrical

shell (Figure 17). The volume contribution of this cylindrical shell is approximately

2πx  f (x)  Δx. Summing the contributions from all the cylindrical shells and let-

ting N tend to inﬁnity, we obtain V 5

2π xfðxÞdx: We summarize our ﬁndings in

the following theorem.

THEOREM 4

(The Method of Cylindrical Shells: Rotation About the y-axis) Let

f be a nonnegative continuous function on an interval [a, b] of nonnegative

numbers. Let V denote the volume of the solid generated when the region below

the graph of f and above the interval [a, b] is rotated about the y-axis. Then,

V 5 2π

xfðxÞdx:

⁄ EX

AMPLE 8 Calculate the volume generated when the region bounded

by y 5 x

1 x

, the x-interval [0, 1], and the vertical line x 5 1 is rotated about the

y-axis.

Solution Theorem

4 applies with f (x) 5 x

1 x

, a 5 0 and b 5 1:

V 5 2π

x ðx

1 x

Þdx 5 2π

ðx

1 x

Þdx 5 2π







x51

x50

π: ¥

INSIGHT

In principle, we could have done this problem by the method of washers

(Figure 18). The formula would have been

V 5 π



2 f

ðyÞ



dy:

However, ﬁnding a formula for f

2 1

( y) would entail solving the cubic equation y 5 x

1 x

for x. Doing so is no easy feat, and the resulting formula is extremely complicated.

We have been able to avoid these difﬁculties by using the method of cylindrical shells.

Cylindrical shell

2pr

m Figure 15

y  f(x)

m Figure 16

f(x)

x

m Figure 17

x  f

1

(y)

y  x

 x

m Figure 18

546 Chapter

7 Applications of the Integral

Similar reasoning applies to the situati on in which we rotate a region between

x 5 g( y ) and the y-axis about the x-axis. We have the following theorem.

THEOREM 5

(The Method of Cylindrical Shells: Rotation About the x-Axis)

Suppose that 0 , c , d. Let g be a nonnegative continuous function on the

interval [c, d] of nonnegative numbers. The volume of the solid generated when

the region bounded by x 5 g( y), the y-axis, y 5 c, and y 5 d is rotated about the

x-axis is

2π

ygðyÞ dy:

⁄ EX

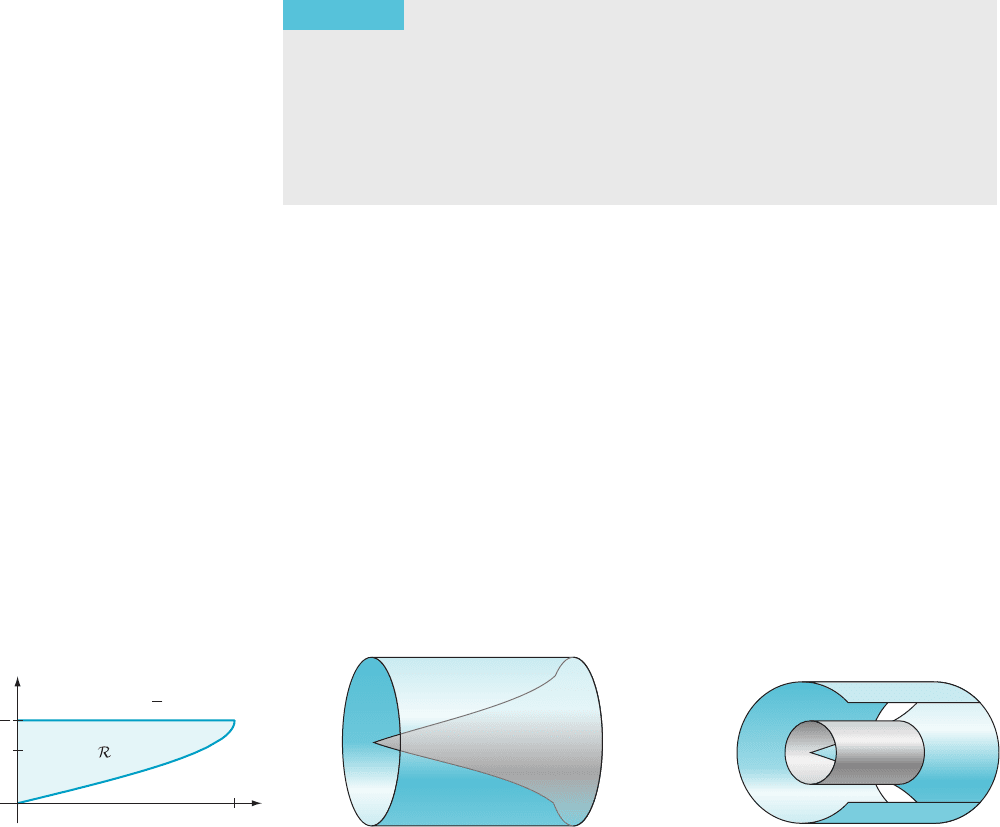
AMPLE 9 Let R be the region that is bounded above by the horizontal

line y 5 π /2, below by the curve y 5 arcsin(x), 0 # x # 1, and on the left by the

y-axis. Use the method of cylindrical shells to calculate the volume V of the solid

that results from rotating R about the x-axis.

Solution Region R is

shown in Figure 19a. When we rotate R about the x-axis we

obtain the solid that lies between the cylinder and the “sorcerer’s hat” that are

shown in Figure 19b. In Figure 19c, we have shifted our perspective a bit and cut

away part of the solid’s outer boundary to reveal one of the cylindrical shells that

we use to calculate the volume. According to Theorem 5 with c 5 0, d 5 π/2, and

g( y) 5 sin( y), we have V 5 2π

π=2

y sinðyÞdy. On integrating by parts with u 5 y

and dv 5 sin( y), dy, we obtain du 5 dy, v 52cos( y), and

V 5 2π

2ycosðyÞ



π=2

cosðyÞdy

5 2π



2y cosðyÞ1 sinðyÞ





π=2

5 2π: ¥

As we have already seen in the case of washers, the methods of this section

apply

to rotation about lines other than the coordinate axes. Here is an example in

the context of cylindri cal shells.

⁄ EX

AMPLE 10 Use the method of cylindrical shells to calculate the volume

of the solid obtained when the region bounded by x 5 y

and x 5 y is rotated about

the line y 5 2.

y  arcsin(x)

x 

m Figure 19a

m Figure 19b

m Figure 19c

7.1 Volumes 547

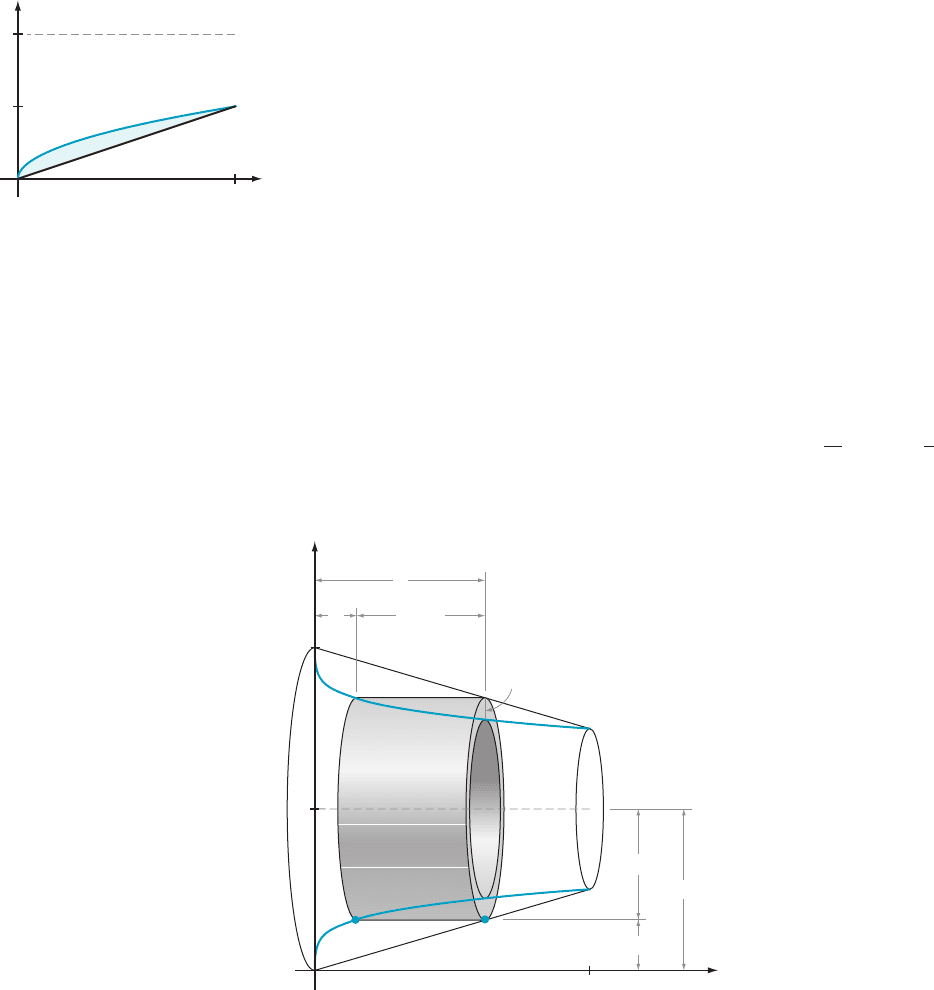
Solution The region that is to be rotated is sketched in Figure 20. The formula of

Theorem 5 does not ap ply on two co unts: The region that we are rotating is not

bounded on the left by the y-axis, and the axis of rotation is not the x-axis. (Either

reason alone would be enough to disqualify the use of the theorem.) Nevertheless,

we can adapt the method of cylindrical shells to the solid at hand. Figure 21 depicts

a cylindrical shell centered about the axis of rotation. Let y denote the height of the

bottom edge, and let Δy denote the thic kness of the shell. Because we will let Δy

tend to 0, the resulting integral will be with respect to the variable y. We notice that

the curves intersect when y 5 0andy 5 1 (Figure 20), so these values will be our

limits of integration. Everything that we need can be deduced from the coordinates

(which we express in terms of the variable of integration) of the points that are

labeled P and Q in Figure 21. The height of the cylinder is y 2 y

and the radius is

2 2 y. The volume V of the solid of revolution is therefore approximately equal to a

sum of terms of the form

2πð2 2 yÞðy 2 y

ÞΔy:

By letting Δy tend to 0, we obtain

V 5

2πð2 2 yÞðy 2 y

Þdy 5 2π

ð2y 2 3y

1 y

Þdy 5 2π



2 y





y51

y50

π: ¥

A Final Remark It is best not to memorize the theorems in this section. It is better to reason about

disks, washers, and cylinders each time you calculate a volume. That way, you will

be sure that you have taken into account the position of the axis of rotation and the

relative positions of the graphs involved.

x  y

m Figure 20

y  y

y

, y)

x  y

2  y

Q(y, y)

x  y

m Figure 21

548 Chapter

7 Applications of the Integral

QUICK QUIZ

1. A region in the xy-plane is rotated about a vertical axis. If the method of disks is

used to calculate the volume of the resulting solid of revolution, what is the

variable of integrat ion?

2. A region in the xy-plane is rotated about a horizontal axis. If the method of

cylindrical shells is used to calculate the volume of the resulting solid of revo-

lution, what is the variable of integration?

3. The region that is bounded above by y 5 sin(x) and below by the interval [0, π]

of the x-axis is rotated about the line x 522. The volume of the resulting solid of

revolution is 2π

φðxÞsinðxÞdx when expressed by the method of cylindrical

shells. What is φ ( x )?

4. The region that is bounded above by y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 x

and below by y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 2 2x

for

0 # x # 4 is rotated about the x-axis. The volume of the resulting solid of revo-

lution is π

ψðxÞdx when expressed by the method of washers. What is ψ (x)?

Answers

1. y 2. y 3. x 1 24

1 2x

EXERCISES

Problems for Practice

c In each of Exercises 126, use the method of disks to cal-

culate the volume V of the solid that is obtained by rotating

the given planar region R about the x-axis. b

1. R is

the region below the graph of y 5

ﬃﬃﬃ

, above the

x-axis, and between x 5 1 and x 5 3.

2. R is the region between the x-axis and the parabola y 5

4 2 x

for 22 # x # 2.

3. R is the region between the x-axis and y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sinðxÞ

;

0 # x # π.

4. R is the region above the x-axis, below the graph of y 5

sec(x), to the right of x 5 0, and to the left of x 5 π/4.

5. R is the region above the x-axis, below the graph of y 5

exp(x), to the right of x 5 0, and to the left of x 5 ln(2).

6. R is the region below the graph of y 5 x

1/3

, above the

x-axis, and between x 5 1 and x 5 8.

c In each of Exercises 7212, use the method of disks to

calculate

the volume V of the solid that is obtained by

rotating the given planar region R about the y-axis. b

7. R is the region in the ﬁrst quadrant that is bounded on

the left by the y-axis, on the right by the graph of

y 5 arcsin(x), and above by y 5 π/2.

8. R is the region in the ﬁrst quadrant that is bounded on the

left by the y-axis, on the right by the graph of x 5 cos( y),

and that is above the line y 5 π /4.

9. R is the region to the right of the y-axis, to the left of the

curve y 5 ln(x), above the x-axis, and below y 5 1.

10. R is the region that is bounded on the left by the y-axis,

on the right by the curve y 5 x

,1# x # 2, and that is

between the horizontal lines y 5 1 and y 5 4.

11. R is the region bounded above by y 5 2, below by y 5

ﬃﬃﬃ

and on the left by the y-axis.

12. R is the region bounded above by y 5 2, below by y 5 1/2,

and between the y-axis and the graph of y 5 1/ x.

c In each of Exercises 13218, use the method of washers to

calculate

the volume V of the solid that is obtained by

rotating the given planar region R about the x-axis. b

13. R is

the region between the curves y 5 x and y 5 x

0 # x # 1.

14. R is the region between the curves y 5 x

and y 5 x

0 # x # 1.

15. R is the region bounded above by the curve y 5 4 2 x

and below by the line y 5 x 1 2.

16. R is the region bounded above by the line y 5 2 and

below by the curve y 5 x

1 1.

17. R is the region bounded above by the line y 5 x 1 1 and

below by the curve y 5 2

18. R is the region bounded above by the line y 5 5 2 x and

below by the curve y 5 6/x.

c In each of Exercises 19224, use the method of washers to

calculate

the volume V obtained by rotating the given planar

region R about the y-axis. b

19. R is

the region between the graphs of x 5 2y and x 5 y

0 # y # 2.

20. R is the region between the curves x 5 y

and x 5 y

0 # y # 1.

21. R is the region that is bounded on the left by the curve

x 5 y

1 2 and on the right by the curve x 5 4 2 y.

22. R is the region between the curves y 5 x 2 1 and

y 5 log

(x), 1 # x # 2.

7.1 Volumes 549

23. R is the region in the ﬁrst quadrant that is bounded on the

left by y 5 4x, on the right by y 5 x

, and above by y 5 4.

24. R is the region between the curves x 5 y

3/2

on the left,

x 5 2y on the right, and y 5 2 below.

c In each of Exercises 25230, use the method of cylindrical

shells

to calculate the volume V of the solid that is obtained

by rotating the given planar region R about the y-axis. b

25. R is

the region below the graph of y 5 exp(x

), above the

x-axis, and between x 5 0 and x 5 1.

26. R is the region bounded above by the curve y 5 2x 2 x

and below by the x-axis.

27. R is the region below the graph of y 5 x

1 1, above the

x-axis, and between x 5 2 and x 5 4.

28. R is the region below the graph of y 5 (1 1 x

)

0 # x # 1 and above the x-axis.

29. R is the region below the graph of y 5 sin(x)/x,0, x # π

and above the x-axis.

30. R is the region below the graph of y 5 2/x,1# x # 2 and

above the x-axis.

c In each of Exercises 31236, use the method of cylindrical

shells

to calculate the volume V of the solid that is obtained

by rotating the given planar region R about the x-axis. b

31. R is

the region in the ﬁrst quadrant that is to the left of

the line y 5 x 2 2 and below y 5 2.

32. R istheregionthatistotherightofthey-axis, to the left of

the curve y 5

ﬃﬃﬃ

, and between the lines y 5 1andy 5 2.

33. R is the region in the ﬁrst quadrant that is to the left of

the curve y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 2 1

and below y 5 1.

34. R is the region that is to the right of the y-axis, to the left

of the curve y 5 216x

, and between the lines y 5 1 and

y 5 8.

35. R is the region between the y-axis and the curve x 5 y

exp( y

), 0 # y # 1.

36. R is the region between the y-axis and the curve

x 5 2 1 y 1 y

,0# y # 2.

c In each of Exercises 37242 use the method of cylindrical

shells

to calculate the volume of the solid that is obtained by

rotating the given planar region R about the y-axis. b

37. R is

the region in the ﬁrst quadrant that is bounded by

y 5 x and y 5 x

38. R is the region between y 5 x, y 5 x

, x 5 2, and x 5 3.

39. R is the region below the graph of y 5 x

1 1, above the

graph of y 5 x , and between x 5 1 and x 5 3.

40. R is the region in the ﬁrst quadrant below the graph of

y 5 1 2 x

and above the graph of y 5 1 2 x.

41. R is the region in the ﬁrst quadrant below the graph of

y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 x

and above the graph of y 5 x 1 1.

42. R is the region below the graph of y 5 4x 2 x

2 2 and

above the graph of y 5 1.

c In each of Exercises 43248, use the method of cylindrical

shells

to calculate the volume V of the solid that is obtained

by rotating the given planar region R about the x-axis. b

43. R is

the region that is bounded by the curve y 5 x

and the

lines y 5 1, y 5 4, and x 5 3.

44. R is the region that is to the right of y 5 5x 2 4, to the left

of y 5 10 2 x

, and above y 5 1.

45. R is the region that is bounded on the left by the curve

y 5 5 2 x

for 2 2 # x #21, on the right by the curve

y 5 5 2 x

for 1 # x # 2, above by the line segment y 5 4

for 2 1 # x # 1, and below by the line segment y 5 1

for 2 2 # x # 2.

46. R is the region that is bounded on the left by the line

y 5 x 1 4 and on the right by the curve x 5 6y 2 y

2 8.

47. R is the region in the ﬁrst quadrant that is bounded by the

y-axis and the curve x 5 4y 2 y

2 3.

48. R is the region in the ﬁrst quadrant that is bounded by the

y-axis and the curve x 5 4y

2 y

2 5y 1 2.

c In each of Exercises 49252, calculate the volume V of

the

solid that is obtained by rotating the planar region between

the curves y 5 x

and y 5 x

1/2

about the given line. b

49. x 5 2

50. x 521

51. y 5 1

52. y 522

c In each of Exercises 53256, R is

the planar region that is

bounded on the left by y 5 4/x

, on the right by x 5 2, and

above by y 5 4. Calculate the volume V of the solid that is

obtained by rotating R about the given line. b

53. x 521

54. x 5 3

55. y 5 4

56. y 521

Further Theory and Practice

c In each of Exercises 57260, use the method of disks to

calculate the volume V of the solid obtained by rotating the

given planar region R about the x-axis. b

57. R is

the region below the graph of y 5 sin(x), 0 # x # π

and above the x-axis.

58. R is the region below the graph of y 5 cos(x), π/6 # x # π /3

and above the x-axis.

59. R is the ﬁrst quadrant region between the x-axis, the

curve y 5

ﬃﬃﬃ

 expðxÞ, and the line x 5 1.

60. R is the region between the x-axis, the curve

y 5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sinðxÞ

; 0 # x # π.

c In each of Exercises 61264, use the method of disks to

calculate

the volume obtained by rotating the given planar

region R about the y-axis. b

61. R is

the region between the curves y 5 exp(x), the y-axis,

and the line y 5 e.

62. R is the ﬁrst quadrant region between the curve y 5

sin(x

), the y-axis, and the line y 5 1.

550 Chapter 7 Applications of the Integral

63. R is the region between the curve y 5 x

/(1 2 x

), the

y-axis, and the line y 5 1/3.

64. R is the region in the ﬁrst quadrant that is bounded by the

coordinate axes and the curve x 5 (1 2 y

)

3/4

c In each of Exercises 65268, use the method of cylindrical

shells

to calculate the volume obtained by rotating the given

planar region R about the given line ‘. b

65. R is

the region between the curves y 5 x

2 4x 2 5 and

y 52x

1 4x 1 5; ‘ is the line x 523.

66. R is the region between the graphs of y 5 exp(x), y 5

x exp(x), and the y-axis; ‘ is the line x 5 1.

67. R is the region between the curves y 5 x

2 x 2 5 and

y 52x

1 x 1 7; ‘ is the line x 5 5.

68. R is the region between the curves x 5 y

and x 52y

; ‘ is

the line y 5 3.

c In each of Exercises 69276, calculate the volume of the

solid

obtained when the region R is rotated about the given

line ‘. b

69. R is

the region between y 5 6 2 x

and y 52x; ‘ is the line

x 524.

70. R is the region that is bounded above by y 5 x

1 3, below

by y 5 2x

2 1, and on the left by x 5 1; ‘ is the line x 5 1.

71. R is the region between the curve y 5 cos(x) and the

x-axis, π/2 # x # 3π/2; ‘ is the line x 5 3π.

72. R is the region in the ﬁrst quadrant that is bounded on the

left by the y-axis, on the right by the curve x 5 tan( y), and

above by the line y 5 π/4; ‘ is the line x 5 1.

73. R is the region bounded by the curve x 5 sin( y), the

y-axis, and the line y 5 π/2; ‘ is the line y 5 2.

74. R is the region between the curves y 5 sin(x) and y 5

cos(x), 0 # x # π/4; ‘ is the line y 5

ﬃﬃﬃ

75. R is

the ﬁrst quadrant region between the curve y 5 x

1 x,

the line x 5 1, and the x-axis; ‘ is the line x 521.

76. R is the ﬁrst quadrant region between the curve y 5 1/

(1 1 x

), the line y 5 1/2, and the y-axis; ‘ is the line x 5 0.

77. Suppose R . r . 0. Calculate the volume of the solid

obtained when the disc {(x, y):x

1 y

# r

} is rotated

about the line x 5 R. (This solid is called a torus)

78. Calculate the volume of the solid obtained when the tri-

angle with vertices (2, 5), (6, 1), (4, 4) is rotated about the

line x 523.

79. Calculate the volume obtained when the region outside the

square {(x, y):|x| , 1, |y| , 1} and inside the circle {(x, y):

1 y

# 4} is rotated about the line y 523.

80. A solid has as its base the ellipse x

1 4y

5 16. The ver-

tical slices parallel to the line y 5 2x are equilateral tri-

angles. Find the volume.

81. The base of a solid S is the disk x

1 y

# 25. For each

k A [25, 5], the plane through the line x 5 k and perpendicular

to the xy-plane intersects S in a square. Find the volume of S.

82. A solid has as its base the region bounded by the parabola

x 2 y

528 and the left branch of the hyperbola

2 y

2 4 5 0. The vertical slices perpendicular to the

x-axis are squares. Find the volume of the solid.

83. Old Boniface, he took his cheer, Then he drilled a hole in

a solid sphere, Clear through the center straight and

strong And the hole was just 10 inches long. Now tell us

when the end was gained What volume in the sphere

remained. Sounds like you’ve not been told enough. But

that’s all you need, it’s not too tough.

84. An open cylindrical beaker with circular base has

height L and radius r. It is partially ﬁlled with a volume

V of a ﬂuid. Consider the parameters L, r,andV to be

constant. T he axis of symmetry of the beaker is along

the positive y-axis and one diameter o f its base is along

the x-axis. When the tank is revolved about the y-axis

with angular speed ω, the surface of the ﬂuid as sumes a

shape that is the paraboloid of revolution that results

when the curve

y 5 h 1 ω

=ð2gÞ; 0 # x # r

is revolved about the y-axis. This formula is valid for

angular speeds at which the surface of the ﬂuid has not yet

touched the base or the mouth of the beaker. The number

h 5 h(ω)isintheinterval[0,V/(πr

)] and depends on ω.

(When ω 5 0, then h 5 V/(πr

). As ω increases, h

decreases.)

a. Find a formula for h(ω).

b. At what value ω

of ω does spilling begin, assuming

that h(ω) . 0 for ω . ω

c. At what value ω

of ω does the surface touch the

bottom of the beaker, assuming that spilling does not

occur for ω , ω

d. As ω increases, does the surface of the ﬂuid touch the

bottom of the beaker or the mouth of the beaker ﬁrst?

Calculator/Computer Exercises

85. The region below the graph of y 5

ﬃﬃﬃ

and above the

graph of y 5 x exp(x) is rotated about the y-axis. Use

Simpson’s Rule from Section 5.8 in Chapter 5 to calculate

the resulting volume to four decimal places.

86. The region below the graph of y 5 exp(2x

), 2 1 # x # 1

is rotated about the x-axis. Use Simpson’s Rule to cal-

culate the resulting volume to four decimal places.

87. A ﬂashlight reﬂector is made of an aluminum alloy whose

mass density is 3.74 g/cm

. The reﬂector occupies the solid

region that is obtained when the region bounded by y 5

2:05

ﬃﬃﬃ

1 0:496; y 5 2:05

ﬃﬃﬃ

1 0:546, x 5 0, and x 5 2.80 cm

is rotated about the x-axis. What is the mass of the

reﬂector?

88. The equation of the St. Louis Gateway Arch is

y 5 693:8597 2 34:38365 ðe

1 e

2kx

for k 5 0.0100333 and 2299.2239 , x , 299.2239, where

both x and y are measured in feet. Rotate this curve about

its vertical axis of symmetry and compute the resulting

volume.

7.1 Volumes 551

7.2 Arc Length and Surface Area

Just as we have approximated area by a sum of areas of rectangles, so can we

approximate the length of a curve by a sum of lengths of line segments. This process

leads to an integral that is used to calculate the length of a graph of a function.

Analogous ideas can also be applied to calculate the area of a surface of revolution.

The Basic Method for

Calculating Arc Length

Suppose that f is a function with continuous derivative on a domain that contains

the interval [a, b]. Let us calculate the length L of the graph of f over this interval.

Fix a positive integer N, and let a 5 x

, x

, ..., x

N21

, x

5b be a uniform

partition of the interval [a, b]. As Figure 1 suggests, we will use a piecewise linear

curve to approximate the graph of f. To be speciﬁc, we will use the line segment

with endpoints P

j21

5 (x

j21

, f (x

j21

)) and P

5 (x

, f (x

)) to approximate the part of

the graph of f that lies over the j

subinterval [x

j21

, x

] (see Figure 2). The length ‘

of this line segment then approximates the length of the arc of the graph between

j21

and P

. We sum the lengths ‘

to obtain an approximate length for the curve:

L 

j51

‘

The accuracy of this approximation is improved by increasing the number N

of subintervals (Figure 3). As N increases to inﬁnity and Δx tends to 0, these

approximating sums tend to what we think of as the length of the curve:

L 5 lim

N-N

j51

‘

: ð7 :2:1Þ

We will use equation (7.2.1) to deﬁne the length L of the graph of f. Of course, we

must ﬁnd an analytic form of the right side that is suitable for calculation.

Refer again to Figure 2. Notice that the length ‘

is given by the usual planar

distance formula:

‘

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðx

2 x

j21



f ðx

Þ2 f ðx

j21



We denote the quantity x

2 x

j21

by Δx and apply the Mean Value Theorem to the

expression f (x

) 2 f (x

j21

) to obtain f (x

) 2 f (x

j21

5 f

)Δx for some s

between

j21

and x

. Now we may rewrite the formula for ‘

‘

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðΔxÞ

1 ðf

ðs

ÞΔxÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðs

Δx:

If we use this formula to substitute for ‘

in equation (7.2.1), then we have

L 5 lim

N-N

j51

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðs

Δx: ð7:2:2Þ

Because the sums on the right side of equation (7.2.2) are Riema nn sums for the

integral

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðxÞ

dx, we conclude that this integral is the value of limit for-

mula (7.2.2) for L. These observations lead to the following deﬁnition.

y  f (x)

x

 bx

a  x

m Figure 1

y  f (x)

f (x

)  f (x

j1

)

ᐉ

x

j1

m Figure 2

y  f(x)

 b

a  x

m Figure 3

552 Chapter

7 Applications of the Integral

DEFINITION

If f has a continuous derivative on an interval containing [a, b],

then the arc length L of the graph of f over the interval [a, b] is given by

L 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðxÞ

dx: ð7:2:3Þ

Some Examples

of Arc Length

The formula for arc length leads to integrals that are often difﬁcult or impossible to

evaluate exactly. In such cases, the techniques of numerical integration that we

studied in Section 5.8 in Chapter 5 may be used to obtain accurate approximations.

In the present section, we concentrate on simple examples in which the integral s

work out neatly.

⁄ EX

AMPLE 1 Calculate the arc length L of the graph of f (x) 5 2x

3/2

over

the interval [0, 7].

Solution By

deﬁnition, the length is

L 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðxÞ

dx 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 ð3x

1=2

dx 5

ð1 1 9xÞ

1=2

dx:

In this last integral, we make the change of variable u 5 1 1 9x, du 5 9 dx and note

that u varies from 1 to 64 as x varies from 0 to 7. The result is

L 5

1=2

du 5



3=2



u564

u51



3=2

2 1



ð512 2 1 Þ5

1022

: ¥

⁄ EX

AMPLE 2 Calculate the length L of

the graph of the function f (x) 5

1 e

)/2 over the interval [1, ln(8)].

Solution We

ﬁrst calculate that f

(x) 5 (e

2 e

)/2 and

1 1 f

ðxÞ

5 1 1

ðe

2 e

4 1 e

2 2 1 e

22x

1 2 1 e

22x



1 e



Thus

L 5

lnð8Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 f

ðxÞ

dx 5

lnð8Þ



1 e



dx 5

2 e



lnð8Þ



8 2





e 2



: ¥

Sometimes an arc length problem is more conveniently solved if we think of

the

curve as being the graph of x 5 g( y).

DEFINITION

If g has a continuous derivative on an interval con taining [c, d ],

then the arc length L of the graph of x 5 g( y) for c # y # d is given by

L 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 g

ðyÞ

dy: ð7:2:4Þ

This is only a restatement of the deﬁnition of arc length and does not

require additional analysis.

7.2 Arc Length and Surface Area 553

⁄ EXAMPLE 3 Calculate the length L of that portion of the graph of the

curve 9x

5 4y

between the points (0, 0) and (2/3, 1).

Solution We

express the curve as x 5 (2/3)y

3/2

and set g( y) 5 (2/3)y

3/2

. Then

( y) 5 y

1/2

. Formula (7.2.4) becomes

L 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 ðy

1=2

dy 5

ð1 1 yÞ

1=2

dy:

This integral can be evaluated easily by means of the substitution u 5 1 1 y,

du 5 dy. Noting that the limits of inte gration for u corres ponding to x 5 0 and x 5 1

are u 5 1 and u 5 2, respectively, we have

L 5

1=2

du 5

3=2



u52

u51



ﬃﬃﬃ

2 1



: ¥

INSIGHT

In Example 3, we might have solved the equation 9x

5 4y

for y and

obtained y 5





2=3

. Setting f ðxÞ5





2=3

, we would obtain f

ðxÞ5





2=3



21=3





21=3

, and L would be given by

L 5

2=3



1 1





22=3



1=2

dx:

This integral would have been considerably more difﬁcult to evaluate! (If you wish to try

your hand at it, then consider the indirect substitution x 5 ð2=3Þtan

ðθÞ.) In general,

there is no method for predicting whether it is advantageous to set up an arc length

integral in a particular way. The fact is, it is usually impossible to calculate arc length

exactly whichever variable of integration is chosen.

Parametric Curves The ideas that we have developed for the arc length of the graph of

y 5 f ð x Þ or x 5 gðyÞ can also be applied to a general parameterized curve. Recall

from Section 1.5 in Chapter 1 that a parametric curve consists of the points (x, y)

arising from parametric equations x 5 ϕ

ðtÞ and y 5 ϕ

ðtÞ. Supposing that ϕ

ðtÞ and

ðtÞ have continuous derivatives on an interval that contains I 5 [α, β], we cal-

culate the length of the parametric curve C 5 f



ðtÞ; ϕ

ðtÞ



: α # t # βg as follows.

For a ﬁxed positive integer N, let α 5 t

, t

, ..., t

N21

, t

5 β be the

order N uniform partition of I. We use the line segment with endpoints

j21

5 (ϕ

j21

), ϕ

j21

)) and P

5 (ϕ

), ϕ

)) to approximate the part of C

corresponding to values of t in the j

subinterval [t

j21

, t

]ofI (see Figure 4). The

length

‘

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðΔxÞ

1 ðΔyÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



Δx

Δt





Δy

Δt



Δt

of this line segment then approximates the length of the arc of C between P

j21

and

. By expressing Δx in terms of ϕ

and Δy in terms of ϕ

, we have

‘

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



ðt

Þ2 ϕ

ðt

j 2 1

Δt





ðt

Þ2 ϕ

ðt

j 2 1

Δt



Δt:

554 Chapter 7 Applications of the Integral