Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


continuous on [0, 8], we may not apply the Fundamental Theorem of Calculus directly to
R
8
0
f ðxÞdx. Nevertheless, it so happens that in this case, as in many others, the correct
answer does result from such an application. That is because, in Example 1, the anti-
derivative F(x)off (x) is continuous at the singularity b 5 8. In general, if a continuous
integrand f is infinite at b, and if the antiderivative F of f on [a, b) is continuous at b, then
Z
b
a
f ðxÞdx 5 lim
ε-0
1
Z
b2ε
a
f ðxÞdx 5 lim
ε-0
1
Fð b 2 εÞ2 FðaÞ
5
ðcontinuityÞ
FðbÞ2 FðaÞ:
This is precisely the answer that would have resulted had we applied the Fundamental
Theorem of Calculus directly to the improper integral
R
b
a
f ðxÞdx without justification. Of
course, the continuity of F at an endpoint singularity of f should not be taken for granted.
⁄ EXAMPLE 2 Analyze the integral
R
3
1
ðx 2 3Þ
22
dx:
Solution This
is an improper integral with infinite integrand at 3. We evaluate this
integral by considering
lim
ε-0
1
Z
32ε
1
1
ðx23Þ
2
dx 5 lim
ε-0
1
2ðx 2 3Þ
21
32ε
1
5 lim
ε-0
1
ðε
21
2 2
21
Þ
51N:
We conclude that the given improper integral diverges.
¥
An improper integral with inte grand that is infinite at the left endpoint of
integration is handled in a manner similar to the right endpoint case.
DEFINITION
If f (x) is continuous on (a, b] and unbounded as x approaches a
from the right, then the value of the improper integral
R
b
a
f ðxÞdx is defined by
Z
b
a
f ðxÞdx 5 lim
ε-0
1
Z
b
a1ε
f ðxÞdx; ð6:6:2Þ
provided that this limit exists and is finite. In this case, the integral is said to
converge. Otherwise, the integral is said to diverge. Figure 3 illustrates this idea.
⁄ EX
AMPLE 3 Evaluate
R
9
0
x
21=2
dx:
Solution This
integral is improper with infinite integrand at 0. Following the
definition, we calculate
Z
9
0
x
21=2
dx 5 lim
ε-0
1
Z
9
01ε
x
21=2
dx 5 lim
ε-0
1
2x
1=2
9
ε
5 lim
ε-0
1
2
ffiffiffi
9
p
2 2
ffiffiffi
ε
p
5 6: ¥
Integrands with Interior
Singularities
An integrand frequently has a singularity at an interior point of an interval of
integration. In these circumstances, we divide the interval of integrat ion into two
subintervals, one on each side of the singularity. We then integrate over each
subinterval separately. If both of these integrals converge, then the original integral
is said to converge. Otherwise, we say that the original integral diverges.
a e
f
ab
m Figure 3 The improper inte-
gral
R
b
a
f ðxÞdx is defined to be the
limit of the area of the shaded
region as a 1 ε approaches a.
6.6 Improper Integrals—Unbounded Integrands 515

⁄ EXAMPLE 4 Evaluate the improper integral
R
2
23
8ðx 1 1Þ
21=5
dx:
Solution The
integrand is unbounded as x tends to 21. Therefore we evaluate
separately the two improper integrals
R
21
23
8ðx 1 1Þ
21=5
dx and
R
2
21
8ðx 1 1Þ
21=5
dx.
For the first of these, we have
Z
21
23
8ðx 1 1Þ
21=5
dx 5 lim
ε-0
1
Z
212ε
23
8ðx 1 1Þ
21=5
dx 5 lim
ε-0
1
8ðx 1 1 Þ
4=5
4=5
212ε
23
5 10 lim
ε-0
1
ð2εÞ
4=5
2 ð22Þ
4=5
5210 2
4=5
:
The second integral is evaluated in a similar way:
Z
2
21
8ðx 1 1 Þ
21=5
dx 5 lim
ε-0
1
Z
2
211ε
8ðx 1 1Þ
21=5
dx 5 lim
ε-0
1
8ðx 1 1Þ
4=5
4=5
2
211ε
5 10 lim
ε-0
1
ð3
4=5
2 ε
4=5
Þ5 10 3
4=5
:
We conclude that the original integral converge s and
Z
2
23
8ðx 1 1Þ
21=5
dx 5
Z
21
23
8ðx 1 1Þ
21=5
dx 1
Z
2
21
8ðx 1 1 Þ
21=5
dx
5210 2
4=5
1 10 3
4=5
5 10
3
4=5
2 2
4=5
: ¥
It is dangerous to try to save work by not dividing the integral at the singularity.
The
next example illustrates what can go wrong.
⁄ EX
AMPLE 5 Evaluate the improper integral
R
2
22
x
24
dx:
Solution What
we should do is divide the given integral into the two integrals
R
0
22
x
24
dx and
R
2
0
x
24
dx: Suppos e that instead we try to save work and just
antidifferentiate:
Z
2
22
x
24
dx 52
1
3
x
23
2
22
52
1
3
1
8
2
1
28
52
1
12
:
Clearly something is wrong. The function x
24
is positive; hence, its integral, if it
exists, should be positive too. What has happened is that an incorrect method has
led to an incorrect negative answer. In fact, the calculation
lim
ε-0
1
Z
02ε
22
x
24
dx 5 lim
ε-0
1
2
1
3
x
23
2ε
22
5 lim
ε-0
1
1
3ε
3
2
1
24
51N
shows that
R
0
22
x
24
dx diverges. Therefore by definition, the improper integral
R
2
22
x
24
dx also diverges. The moral of this example is always to divide an integral at
an interior singularity.
¥
INSIGHT
In Example 5, we determined that
R
2
22
x
24
dx is divergent by integrating on
only one side of the singularity at 0. A calculation similar to that of
R
0
22
x
24
dx would have
shown that
R
2
0
x
24
dx also diverges. That calculation turned out to be unnecessary and was
therefore omitted. For a conclusion of divergence, it is enough to show that the integral
diverges on one side of the singularity. By contrast, for a conclusion of convergence,we
must show that the integrals on both sides of an interior singularity converge.
516 Chapter 6 Techniques of Integration

Integrands That Are
Unbounded at Both
Endpoints
When an integrand f is continuous on an open interval (a, b) and unbounded at both
endpoints a and b, then we choose an interior point c — any interior point will do—
and investigate the two improper integrals
R
c
a
f ðxÞdx and
R
b
c
f ðxÞdx: If both converge,
then
R
b
a
f ðxÞdx is said to converge. In this case,
R
b
a
f ðxÞdx is defined to be the sum
R
c
a
f ðxÞdx 1
R
b
c
f ðxÞdx. The value of this sum does not depend on the particular
interior point c that has been chosen. If one of the two integrals,
R
c
a
f ðxÞdx and
R
b
c
f ðxÞdx diverges, or if both diverge, then we say that
R
b
a
f ðxÞdx also diverges.
⁄ EX
AMPLE 6 Determine whether the improper integral
Z
1
0
1
xð1 2 xÞ
1=3
dx
converges or diverges.
Solution The
integrand of the given integral is singular at both endp oints 0 and 1.
Accordingly, we choose c 5 1/2 (or any other point between the limits of integra tion)
and begin our analysis with the improper integral
Z
1=2
0
1
xð1 2 xÞ
1=3
dx: Notice that
0 , ð1 2 xÞ
1=3
, 1for0, x , 1. Therefore 1 , ð1 2 xÞ
21=3
and
1
x
,
1
xð1 2 x Þ
1=3
for 0 , x , 1. It follows that
Z
1=2
0
1
xð1 2 xÞ
1=3
dx 5 lim
ε-0
1
Z
1=2
ε
1
xð1 2 xÞ
1=3
dx $ lim
ε-0
1
Z
1=2
ε
1
x
dx 5 lim
ε-0
1
ln
1
2
2 lnðεÞ
5 N;
because lim
ε-0
1
lnðεÞ52N. We conclude that
Z
1=2
0
1
xð1 2 xÞ
1=3
dx diverges.
Because one of the component integrals of
Z
1
0
1
xð1 2 xÞ
1=3
dx diverges, we con-
clude that the full integral on [0, 1] diverges.
¥
INSIGHT
If f is unbounded at both a and b, and if c is a point between, then it does
not matter which of
R
c
a
f ðxÞdx or
R
b
c
f ðxÞdx is examined first. If the first integral analyzed
is divergent (as in Example 6), then
R
b
a
f ðxÞdx diverges; an investigation of the behavior
on the other side of c is not needed in this case. However, if the first integral analyzed is
convergent, then it is the integral on the other side of c that tells you the behavior of
R
b
a
f ðxÞdx: In Example 6, had we initiated our investigation of
Z
1
0
1
xð1 2 xÞ
1=3
dx with
Z
1
1=2
1
xð1 2 xÞ
1=3
dx, we would have found the integral to the right of 1/2 convergent
(Exercise 63). No conclusion would have been possible from that information. We would
have had to turn to the integral to the left of 1/2 before coming to a conclusion.
Proving Convergence
Without Evaluation
Suppose that f and g are continuous, positive functions on [a, b), unbounded as
x -b
2
and that 0 # f ðxÞ# gðxÞ for all a , x , b. If we are able to find an anti-
derivative of g and use it to show that lim
ε-0
1
R
b2ε
a
gðxÞdx exists and is finite, then
6.6 Improper Integrals—Unbounded Integrands 517

we may assert the same conclusions for f. The reason is that
R
b2ε
a
f ðxÞdx increases
as ε decreases (because f is positive and the area under its graph increases as its
right endpoint moves further to the right). Furthermore,
R
b
a
gðxÞdx is an upper
bound for these integrals because
Z
b2ε
a
f ðxÞdx #
Z
b2ε
a
gðxÞdx #
Z
b
a
gðxÞdx , N:
It follows from the completeness property of the real numbers that
lim
ε-0
1
R
b2ε
a
f ðxÞdx exists and is finite. The next theorem states this observation in
a somewhat more general form.
THEOREM 1
(Comparison Theorem for Unbounded Integrands) Suppose that
f and g are continuous functions on the interval (a, b), that 0 # f ðxÞ# gðxÞ for all
a , x , b, and that f (x)andg(x) are unbounded as x-a
1
; or as x-b
2
; or as
x-a
1
and x-b
2
:
a. If
R
b
a
gðxÞdx is convergent, then
R
b
a
f ðxÞdx is also convergent and
R
b
a
f ðxÞdx #
R
b
a
gðxÞdx:
b. If
R
b
a
f ðxÞdx is divergent, then
R
b
a
gðxÞdx is also divergent.
Notice that the Comparison Theorem does not sayanythingabout
R
b
a
f ðxÞdx
if
R
b
a
gðxÞdx is convergent and g is less than f. To use the Comparison Theorem to
show that an improper integral
R
b
a
f ðxÞdx is convergent, we must find a function g
that is greater than or equal to f and for which
R
b
a
gðxÞdx is convergent. If A and p
are positive constants with p , 1, then g(x) 5 A/x
p
is often a useful comparison
function for proving convergence on an interval of the form [0, b]. See Exercise 55.
With the same constraints on A and p,thefunctiong(x) 5 A/(b 2 x)
p
is often a useful
comparison function for proving convergence on the interval [a, b]. See Exercise 56.
⁄ EX
AMPLE 7 Show that the improper integral
Z
9
0
1 1 cosðx
2
Þ
ffiffiffi
x
p
dx is
convergent.
Solution T
he integrand f ðxÞ5
1 1 cosðx
2
Þ
=
ffiffiffi
x
p
is unbounded at its left endpoint
a 5 0. Consequently, formula (6.6.2) applies. The problem is that we cannot find an
antiderivative for f (x). As a result, we cannot calculate
R
9
01ε
f ðxÞdx.Wetherefore
need an indirect way to show that
R
9
0
f ðxÞdx is convergent. The solution is to find a
simpler function g to which we can compare f. To that end, we replace the numerator
of f with something that is less complicated. Because 21 # cosðx
2
Þ# 1, we have
0 #
1 1 cosðx
2
Þ
ffiffiffi
x
p
#
2
ffiffiffi
x
p
:
We therefore take gðxÞ5 2=
ffiffiffi
x
p
as the function for comparison. From Example 3,
we see that
R
9
0
gðxÞdx 5 2
R
9
0
x
21=2
5 12. Therefore by the Comparison Theorem, we
conclude that
Z
9
0
1 1 cosðx
2
Þ
ffiffiffi
x
p
dx is convergent and
Z
9
0
1 1 cosðx
2
Þ
ffiffiffi
x
p
dx # 12 .
b
518 Chapter
6 Techniques of Integration

INSIGHT
The upper bound
R
b
a
gðxÞdx stated in part a of the Comparison Theorem is
not necessarily a good approximation of
R
b
a
f ðxÞdx: For example, numerical techniques
show that
Z
9
0
1 1 cosðx
2
Þ
ffiffiffi
x
p
dx 7:663; which is quite a bit smaller than 12, the upper
bound obtained in Example 7. Nevertheless, the Comparison Theorem can be used as
part of an effective approximation strategy. See Exercises 7277.
QUICK QUIZ
1. Calculate
R
9
0
x
21=2
dx:
2. Calculate
R
16
0
ð16 2 x Þ
21=4
dx:
3. True or false: If f is unbounded at both a and b, and if c is a point in between,
then
R
b
a
f ðxÞdx is divergent if and only if both
R
c
a
f ðxÞdx and
R
b
c
f ðxÞdx are
divergent.
4. Use the Comparison Theorem to determine which of the following improper
integrals converge:
a)
Z
π=4
0
secðxÞ
x
2
dx; b)
Z
8
21
x
4=3
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
dx; c)
Z
1
0
expðxÞ
ffiffiffi
x
p
dx; d)
Z
1
0
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
x
dx:
Answers
1. 6 2. 32/3 3. False 4. (b) and (c)
EXERCISES
Problems for Practice
c In each of Exercises 1210, determine whether the given
improper integral is convergent or divergent. If it converges,
then evaluate it. b
1.
R
5
1
ðx 2 5Þ
24=3
dx
2.
Z
22
23
1
x 1 2
dx
3.
R
4
2
ð4 2 xÞ
20:9
dx
4.
R
2
1
ðx 2 2Þ
21=5
dx
5.
R
π=2
0
tanðxÞdx
6.
R
π=2
0
sec
2
ðxÞdx
7.
Z
1
0
x
ð1 2 x
2
Þ
1=4
dx
8.
Z
1
0
1
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
dx
9.
Z
2
0
1
4 2 x
2
dx
10.
Z
21
22
1
x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
x
2
2 1
p
dx
c In each of Exercises 11220, determine whether the given
improper
integral is convergent or divergent. If it converges,
then evaluate it. b
11.
R
2
23
ðx 1 3Þ
21:1
dx
12.
R
0
24
ðx 1 4Þ
20:1
dx
13.
R
8
0
x
21=3
dx
14.
R
3
21
ðx 1 1Þ
23
dx
15.
Z
1
0
lnðxÞ
x
dx
16.
Z
13
4
1
ffiffiffiffiffiffiffiffiffiffiffi
x 2 4
p
dx
17.
R
3
0
x
21=2
ð1 1 xÞdx
18.
Z
e
1
1
x ln
1=3
ðxÞ
dx
19.
R
1
0
lnðxÞdx
20.
Z
ffiffi
2
p
1
1
x
ffiffiffiffiffiffiffiffiffiffiffiffiffi
x
2
2 1
p
dx
c In each of Exercises 21230, determine whether the given
improper
integral is convergent or divergent. If it converges,
then evaluate it. b
21.
Z
2
0
1
x 2 1
dx
22.
R
3
21
6x
21=7
dx
23.
Z
21
25
3
ðx 1 3Þ
2=5
dx
6.6 Improper Integrals—Unbounded Integrands 519
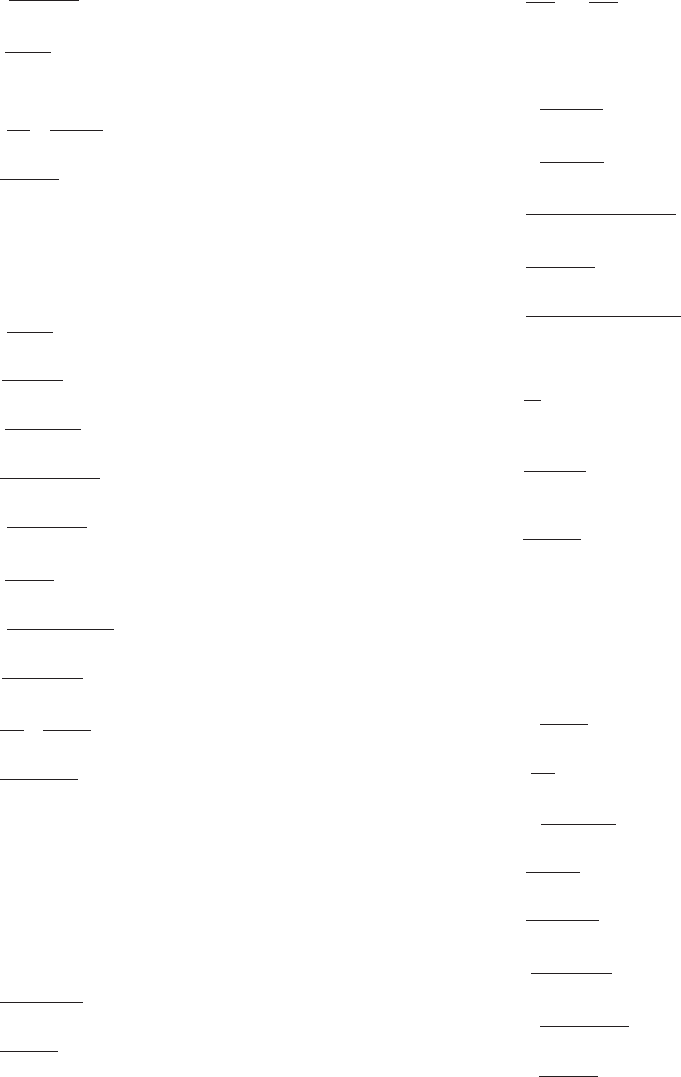
24.
R
6
3
ðx 2 4Þ
22
dx
25.
R
4
22
ðx 1 1Þ
22=3
dx
26.
Z
e
1=e
1
x ln
2=7
ðxÞ
dx
27.
Z
3
0
x
x
2
2 2
dx
28.
R
3
23
x
21=3
ðx 1 1Þdx
29.
Z
16
1
1
ffiffiffi
x
p
1
2 2
ffiffiffi
x
p
1=3
dx
30.
Z
2
0
1
1 2 x
1=3
dx
c In each of Exercises 31240, determine whether the given
improper
integral is convergent or divergent. If it converges,
then evaluate it. b
31.
Z
1
21
1
1 2 x
2
dx
32.
Z
2
22
1
ffiffiffiffiffiffiffiffiffiffiffiffiffi
4 2 x
2
p
dx
33.
Z
1
0
1
ffiffiffi
x
p
ð1 2 xÞ
dx
34.
Z
2
1
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3x 2 x
2
2 2
p
dx
35.
Z
1
21
x
ð1 2 x
2
Þ
1=4
dx
36.
Z
1
0
1
xlnðxÞ
dx
37.
Z
4
21
1
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p ffiffiffiffiffiffiffiffiffiffiffi
4 2 x
p
dx
38.
Z
0
21
3
x
1=3
ðx 1 1Þ
dx
39.
Z
4
0
1
ffiffiffi
x
p
1
22
ffiffiffi
x
p
1=3
dx
40.
Z
1
0
1
ffiffiffi
x
p
ffiffiffiffiffiffiffiffiffiffiffi
1 2 x
p
dx
Further Theory and Practice
c In each of Exercises 41254, determine whether the given
improper integral is convergent or divergent. If it converges,
then evaluate it. b
41.
R
2
25
lnðx 1 5Þdx
42.
Z
1
0
expð21=xÞ
x
2
dx
43.
Z
2
0
ln
1=3
ðxÞ
x
dx
44.
R
1
0
ln
2
ðxÞdx
45.
R
4
0
x
21=2
lnðxÞdx
46.
R
9
0
x
23=2
lnðxÞdx
47.
Z
8
0
1
x
1=3
ln
1
x
1=3
dx
48.
R
3
21
lnðjxjÞdx
49.
R
1
21
lnð1 2 x
2
Þdx
50.
Z
π=2
0
cosðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffi
sinðxÞ
p
dx
51.
Z
π=2
0
cos
3
ðxÞ
sin
1=3
ðxÞ
dx
52.
Z
1
0
1
ð1 1 x
2
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
arctanðxÞ
p
dx
53.
Z
1
0
arcsinðxÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 x
2
p
dx
54.
Z
1
0
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffiffiffiffiffiffiffiffiffiffi
x 1 1
p
2 1
p
ffiffiffiffiffiffiffiffiffiffiffi
x 1 1
p
dx
55. Suppose that p and b are positive numbers. Show that
Z
b
0
1
x
p
dx is convergent if and only if p , 1.
56. Suppose that p is positive and that 0 , a , b. Show that
Z
b
a
1
ðb 2 xÞ
p
dx is convergent if and only if p , 1.
57. For what positive values of p is the improper integral
Z
e
1
1
x ln
p
ðxÞ
dx convergent?
c In each of Exercises 58269 use the Comparison Theorem
to
determine whether the given improper integral is con-
vergent or divergent. In some cases, you may have to break
up the integration before applying the Comparison
Theorem. b
58.
Z
π=2
0
cosðxÞ
ffiffiffi
x
p
dx
59.
Z
1
0
e
x
ffiffiffi
x
p
dx
60.
Z
6
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 1 sinðxÞ
x 2 2
r
dx
61.
Z
3
0
ffiffiffiffiffiffiffiffiffiffiffi
1 1 x
p
x
2=3
dx
62.
Z
1
0
sinðxÞ
ð1 2 xÞ
2=3
dx
63.
Z
1
1=2
1
xð1 2 xÞ
1=3
dx
64.
Z
π=2
0
1
ffiffiffi
x
p
1 sinðxÞ
dx
65.
Z
1=3
0
secðπxÞ
1 2 3x
dx
520 Chapter 6 Techniques of Integration
66.
R
1
0
x
21=2
ð1 2 xÞ
23=4
dx
67.
Z
2
1
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x
3
1 x
2
2 2
p
dx
68.
Z
π=2
0
ffiffiffi
x
p
sinðxÞ
dx
69.
Z
3
1
1
ðx21Þ
5=3
ffiffiffiffiffiffiffiffiffiffiffi
3 2 x
p
dx
70. Evaluate the improper integral
Z
9
5
ffiffiffiffiffiffiffiffiffiffiffi
x 1 7
x 2 5
r
dx by making
the direct substitution u 5 x 2 5 followed by the indirect
substitution u 5 12tan
2
ðθÞ.
71. Suppose that p is positive and q is nonnegative. Let B
denote the beta function defined by
Bðp; qÞ5
Z
1
0
x
211p
ð1 2 xÞ
11q
dx:
a. Show that
Bðp; 0Þ5
1!
pðp 1 1Þ
:
b. For q $ 1, show that
Bðp; qÞ5
1 1 q
p
Bðp 1 1; q 2 1Þ:
c. Use parts a and b to find formulas for B( p, 1) and
B( p, 2).
Calculator/Computer Exercises
c In each of Exercises 72277, the given function f (x)is
unbounded as x -0
1
: Determine a function g (x) 5 cx
p
such
that (a) 0 # f ðxÞ# gðxÞ for each x in (0, 1], and (b)
R
1
0
gðxÞdx is
convergent. This shows that
R
1
0
f ðxÞdx is convergent by the
Comparison Theorem. By determining a positive ε such that
R
ε
0
gðxÞdx , 5 3 10
24
; approximate
R
1
0
f ðxÞdx to three decimal
places. b
72. f ðxÞ5 x
21=2
cosðx
2
Þ
73. f ðxÞ5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 1 1=x
p
74. f ðxÞ5
2 1 sinðxÞ
=x
1=3
75. f ðxÞ5
ffiffiffi
x
p
cscðxÞ
76. f ðxÞ5 arccosðxÞ=x
5=6
77. f ðxÞ5 lnð2 1 xÞ=x
lnð2Þ
6.7 Improper Integrals—Unbounded Intervals
Suppose that we want to calculate the integral of a continuous function over an
unbounded interval of the form (2N, b)or(a , 1N). Like the integrals with
unbounded integrand that we studied in the preceding section, these integrals are
said to be improper. The theory of the integral that you learned in Chapter 5 does
not cover these improper integrals, and some new concepts are needed.
The Integral on an
Infinite Interval
The idea that enables us to define improper integrals over unbounded intervals is
similar to the one we used in the preceding section for imp roper integrals with
unbounded functions. Instead of trying to integrate over an unbounded interval all
at once, we integrate over a bounde d interval and then we let an endpoint tend to
infinity.
DEFINITION
Let f be a continuous function on the interval [a,N). The
improper integral
R
N
a
f ðxÞdx is defined by
Z
N
a
f ðxÞdx 5 lim
N-1N
Z
N
a
f ðxÞdx
provided that the limit exists and is finite. When the limit exists, the integral is
said to converge. Otherwise, it is said to diverge (see Figure 1a). Similarly, if g is
a continuous function on the interval (2N, b), then the value of the improper
integral
R
b
2N
gðxÞdx is defined to be
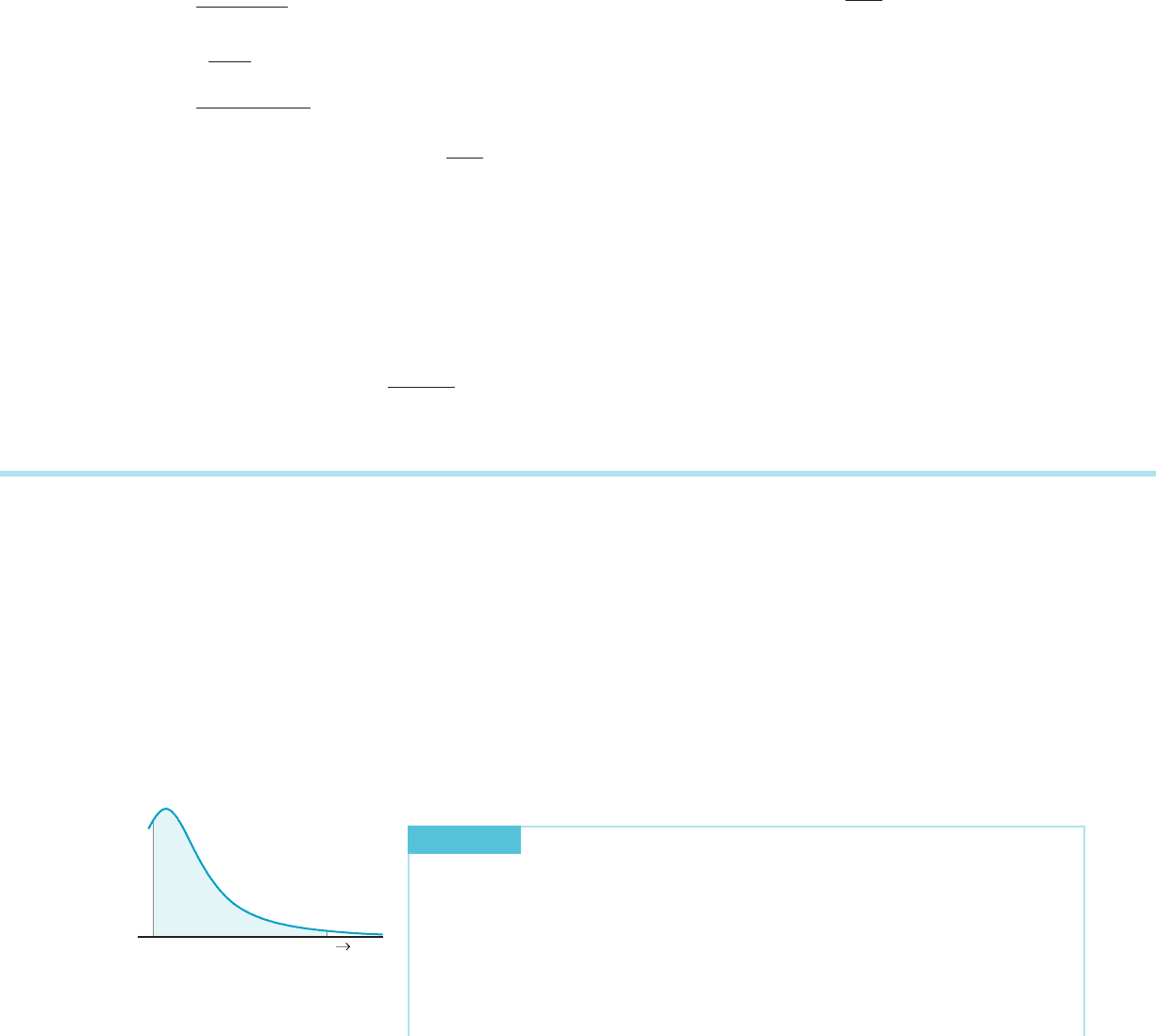
A
f
N
m Figure 1a The improper
integral
R
N
A
f ðxÞdx is defined to
be lim
N-1N
R
N
A
f ðxÞdx:
6.7 Improper Integrals—Unbounded Intervals 521
lim
M-2N
Z
b
M
gðxÞdx
provided that the limit exists and is finite. When the limit exists, the integral is
said to converge. Otherwise it is said to diverge (see Figure 1b).
⁄ EX
AMPLE 1 Calculate the improper integral
R
N
1
x
22
dx:
Solution Accord
ing to the definition, we have
Z
N
1
x
22
dx 5 lim
N-N
Z
N
1
x
22
dx 5 lim
N-N
2
1
x
N
1
5 lim
N-N
2
1
N
2
2
1
1
5 1:
We conclude that the integral converges and has value 1.
b
⁄ EXAMPLE 2 Determine whether the improper integral
R
28
2N
x
21=3
dx
converges or diverges.
Solution We
do this by evaluating the limit
lim
M-2N
Z
28
M
x
21=3
dx 5 lim
M-2N
x
2=3
2=3
28
M
5
3
2
lim
M-2N
ð28Þ
2=3
2 M
2=3
52N:
We conclude that the integral diverges.
¥
INSIGHT
Examples 1 and 2 are concerned with integrands of the form 1/x
p
(with
p 5 2 and p 5 1/3, respectively). In general, if p . 0, then f (x) 5 1/x
p
decays to 0 as x -N.
However, Example 2 shows that the limit property lim
x-N
f ðxÞ5 0 does not by itself
guarantee that
R
N
a
f ðxÞdx converges. In the case of f ðxÞ5 1=x
1=3
, the integrand does not
decay to 0 sufficiently rapidly as x -N: By contrast, 1/x
2
tends to 0 much more quickly,
as Figure 2 shows. This more rapid decay results in the convergence of
R
N
1
ð1=x
2
Þdx; as we
know from Example 1. The next example analyzes the convergence of
R
N
1
ð1=x
p
Þdx in
complete generality.
⁄ EXAMPLE 3 Suppose that a . 0. Show that the improper integral
Z
N
a
1
x
p
dx diverges for 0 , p # 1 and converges for 1 , p .
Solution For p 5 1,
we have
Z
N
a
1
x
p
dx 5 lim
N-N
Z
N
a
1
x
dx 5 lim
N-N
lnðjxjÞj
N
a
5 lim
N-N
lnðNÞ2 lnðaÞ
5 N;
and the improper integral is divergent. For p 6¼1, we have
lim
N-N
Z
N
a
1
x
p
dx 5 lim
N-N
x
12p
12p
N
a
5 lim
N-N
N
12p
1 2 p
1
a
12p
p 2 1
5
a
12p
p 2 1
1 lim
N-N
N
12p
1 2 p
:
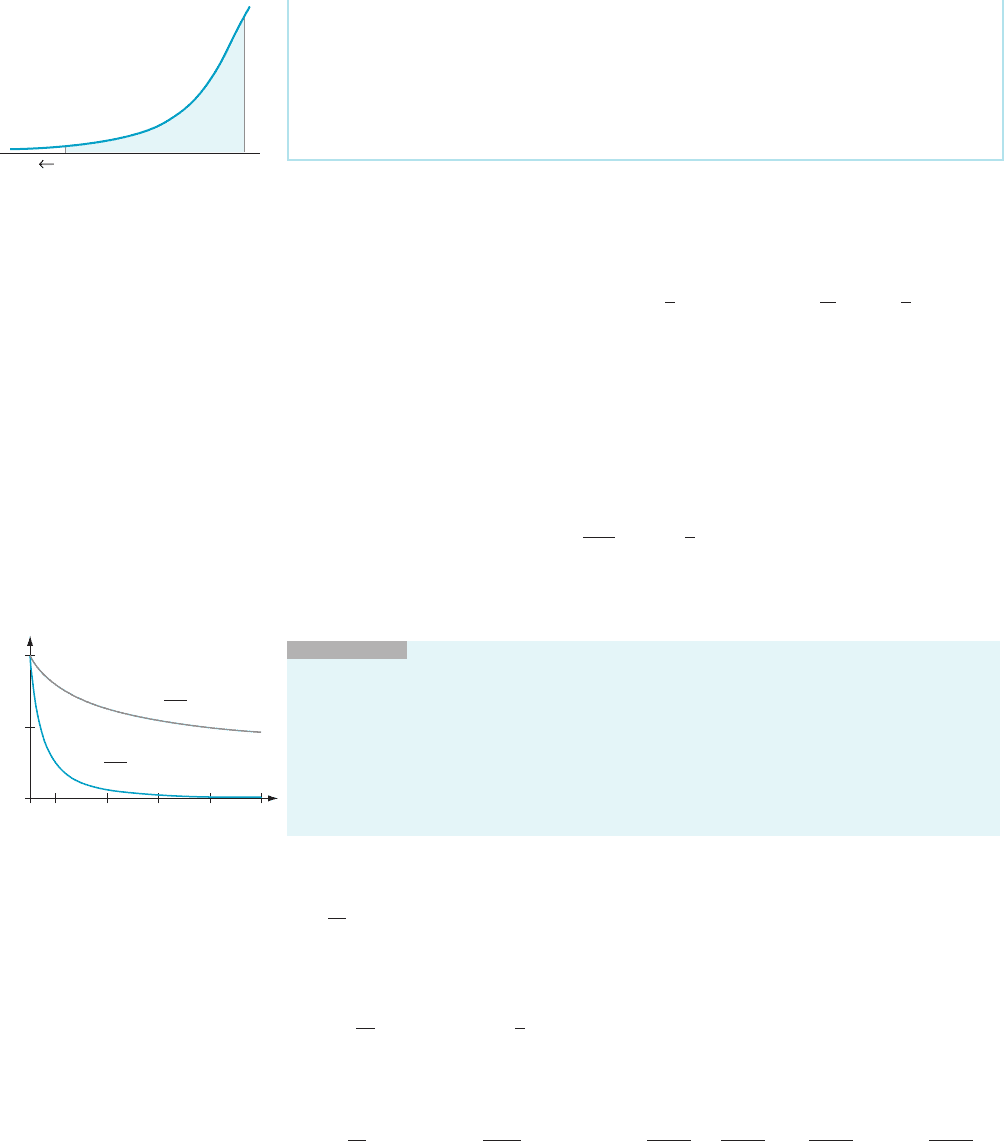
B
g
M
m Figure 1b The improper
integral
R
B
2N
gðxÞdx is defined to
be lim
M-1N
R
B
M
gðxÞdx:
1
0.5
0
246810
y
x
y
x
1/3
1
y
x
2
1
m Figure 2
522 Chapter
6 Techniques of Integration

If 0 , p , 1, then 1 2 p . 0, and lim
N-N
N
12p
5 N: Therefore
Z
N
a
1
x
p
dx is
divergent for 0 , p , 1. If 1 , p, then 0 , p 2 1, and lim
N-N
N
12p
5
lim
N-N
1
N
p21
5 0: It follows that
Z
N
a
1
x
p
dx is convergent for 1 , p. Moreover,
Z
N
a
1
x
p
dx 5
a
12p
p 2 1
:
¥
An Application
to Finance
If an initial investment P
0
is allowed to compound continuously at an annual
interest rate of r percent, then formula (2.6.16) tells us it will grow to P
0
e
rt/100
in
t years. In other words, if we let ρ 5 r/100, then the growth factor is e
ρt
. To attain a
sum equal to P in t years, we must invest Pe
2ρt
now. We say that Pe
2ρt
is the present
value of an amount P that is to be received t years from now. In this context, the
interest rate, r percent, is called the discount rate.
Next, instead of a single payment in the future, consider a future income
stream. We assume that the income will commence T
1
years in the futur e and that it
will terminate at time T
2
. T
1
. Let f (t) denote the rate at which the income arrives
at time t for 0 # T
1
# t # T
2
,N. Let us figure out the present value of this income
stream. Divide the interval [T
1
, T
2
] into small subintervals by means of the uniform
partition T
2
5 t
0
, t
1
, ... , t
N
5 T
2
. If we choose a point s
j
in [t
j21
, t
j
] for each j,
then we can approximate the money earned over the time interval [t
j21
, t
j
]by
f (s
j
) Δt. The present value of this amount is about (f (s
j
) Δt) exp(2ρs
j
). Thus the
present value of the entire income stream is ab out
X
N
j51
f ðs
j
Þexpð2 ρs
j
Þ Δt:
This quantity is a Riemann sum for the integral
R
T
2
T
1
f ðt Þe
2ρ t
dt that results when
N-N and Δt -0. We have found that, if the current annual interest rate is r
percent and ρ 5 r/100, then the present value PV of the income stre am f (t) for
T
1
# t # T
2
is given by
PV 5
Z
T
2
T
1
f ðtÞe
2ρ t
dt:
When an income stream is to continue in perpetuity, we let T
2
tend to infinity. In
other words, the improper integral
R
N
T
1
f ðtÞe
2ρ t
dt is the present value of an income
stream that begins T
1
years in the future and continues in perpetuity. (Such per-
petuities are rare, but they do exist. One British government perpetuity issued in
1752 still trades.)
⁄ EX
AMPLE 4 (Present Value of a Perpetuity) Suppose that a trust is
established that, beginning immediately, pays 2t 1 50 dollars per year in perpetuity,
where t is time measured in years with t 5 0 corresponding to the present. Assuming
a discount rate of 6%, what is the present value of all the money paid out by this
trust account?
Solution Here T
1
5 0, r 5 6, and ρ 5 r/100 5 0.06. The present value PV of the
perpetuity is given by
PV 5
Z
N
0
ð2t 1 50Þe
20:06t
dt 5 lim
N-N
Z
N
0
ð2t 1 50Þ
|fflfflfflfflffl{zfflfflfflfflffl}
u
e
20:06t
dt
|fflfflfflfflffl{zfflfflfflfflffl}
dv
5 lim
N-N
ð2t150Þ
|fflfflfflfflffl{zfflfflfflfflffl}
u
e
20:06t
20:06
|fflfflffl{zfflfflffl}
v
N
0
2
Z
N
0
e
20:06t
2 0:06
|fflfflffl{zfflfflffl}
v
2dt
|{z}
du
!
:
6.7 Improper Integrals—Unbounded Intervals 523

Thus
PV 5 lim
N-N
ð2t 1 50Þ
e
20:06t
20:06
2 2
e
20:06t
ð20 :06Þ
2
N
0
5 lim
N-N
ð2N 1 50Þ
e
20:06N
20:06
2 2
e
20:06N
ð20:06Þ
2
2
ð50Þ
e
20
20:06
2 2
e
20
ð20:06Þ
2
0
@
1
A
5
2
20:06
lim
N-N
Ne
20:06N
2 ð21388:89Þ:
We finish our computation by using l’Ho
ˆ
pital’s Rule to evaluate the limit, which is
the indeterminate form N 0. Thus
lim
N-N
Ne
20:06N
5 lim
N-N
N
e
0:06N
5 lim
N-N
d
dN
N
d
dN
e
0:06N
5 lim
N-N
1
0:06e
0:06N
5 0:
It follows that the present value of the annuity is $1388.89.
¥
Integrals Over the
Entire Real Line
To integrate a continuous functio n f overtheentirerealline(2N,N), we choose a
point c — any point will do—and investigate the two improper integrals
R
c
2N
f ðxÞdx
and
R
N
c
f ðxÞdx: If both converge, then
R
N
2N
f ðxÞdx is said to converge . In this case,
R
N
2N
f ðxÞdx is defined to be the sum
R
c
2N
f ðxÞdx 1
R
N
c
f ðxÞdx: The value of this sum
does not depend on the particular point c that has been chosen. Thus
Z
N
2N
f ðxÞdx 5 lim
M-2N
Z
c
M
f ðxÞdx 1 lim
N-1N
Z
N
c
f ðxÞdx ð6:7:1Þ
provided that both limits exist and are finite. Otherwise we say that
R
N
2N
f ðxÞdx
diverges.
⁄ EX
AMPLE 5 Determine whether the improper integral
Z
N
2N
x
1 1 x
2
dx
converges or diverges.
Solution We
may divide the line at any point. The number 0 makes a natural
choice. We begin our analysis with the improper integral
Z
N
0
x
1 1 x
2
dx: Usin g the
substitution u 5 1 1 x
2
, du 5 2xdx, we calculate
lim
N-N
Z
N
0
x
1 1 x
2
dx 5
1
2
lim
N-N
Z
11N
2
1
1
u
du 5
1
2
lim
N-N
lnðjujÞ
11N
2
1
5
1
2
lim
N-N
lnð1 1 N
2
Þ5 N:
Because
Z
N
0
x
1 1 x
2
dx diverges, we conclude that
Z
N
2N
x
1 1 x
2
dx also diverges. (A
similar computation shows that lim
M-2N
Z
0
M
x
1 1 x
2
dx 52N; but this calculation is
not necessary. If even one of the limits on the right side of (6.7.1) is infinite, then that
is enough to tell us that the integral on the left side of (6.7.1) is divergent.)
¥
524 Chapter
6 Techniques of Integration
