Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

454 Marina Ruths and Jacob N. Israelachvili

smooth and chemically homogenous surfaces supported by perfectly elastic materi-

als. It can be responsiblefor such phenomena as rolling friction and elastoplastic ad-

hesive contacts [239,263–266] during loading–unloadingand adhesion–decohesion

cycles.

Adhesion hysteresis may be thought of as being due to mechanical eﬀects such

as instabilities, or chemical eﬀects such as interdiﬀusion, interdigitation, molecular

reorientations and exchange processes occurring at an interface after contact, as il-

lustrated in Fig. 9.12. Such processes induce roughness and chemical heterogeneity

even though initially (and after separation and re-equilibration) both surfaces are

perfectly smooth and chemically homogeneous. In general, if the energy change, or

work done, on separating two surfaces from adhesive contact is not fully recover-

able on bringing the two surfaces back into contact again, the adhesion hysteresis

Fig. 9.12. (a) Schematic representation of interpenetrating chains. (b)and(c): JKR plots

(contact radius r as a function of applied load L) showing small adhesion hysteresis for un-

crosslinked polystyrene and larger adhesion hysteresis after chain scission at the surfaces

after 18 h irradiation with ultraviolet light in an oxygen atmosphere. The adhesion hystere-

sis continues to increase with the irradiation time. (d) Rate-dependent adhesion of hexadecyl

trimethyl ammonium bromide (CTAB) surfactant monolayers. The solid curves [259] are ﬁts

to experimental data on CTAB adhesion after diﬀerent contact times [260] using an approxi-

mate analytical solution for a JKR model, including crack tip dissipation. Due to the limited

range of validity of the approximation, the ﬁts rely on the part of the experimental data with

low eﬀective adhesion energy only. From the ﬁts one can determine the thermodynamic ad-

hesion energy, the characteristic dissipation velocity, and the intrinsic dissipation exponent

9 Surface Forces and Nanorheology of Molecularly Thin Films 455

may be expressed as

> W

Receding Advancing

ΔW = (W

−W

) > 0 , (9.24)

where W

and W

are the adhesion or surfaceenergies for receding (separating)and

advancing (approaching) two solid surfaces, respectively.

Hysteresis eﬀects are also commonly observed in wetting/dewetting phenom-

ena [267]. For example, when a liquid spreads and then retracts from a surface the

advancing contact angle θ

is generally larger than the receding angle θ

. Since the

contact angle, θ, is related to the liquid–vapor surface tension, γ

, and the solid–

liquid adhesion energy, W, by the Dupré equation,

(1+ cosθ)γ

= W , (9.25)

we see that wetting hysteresis or contact angle hysteresis (θ

>θ

) actually implies

adhesion hysteresis, W

> W

, as given by (9.24).

Energy-dissipatingprocessessuch as adhesion and contactangle hysteresis arise

becauseof practical constraintsof theﬁnite time ofmeasurements andthe ﬁnite elas-

ticity of materials. This prevents many loading–unloading or approach–separation

cycles from being thermodynamically reversible, even though they would be if car-

ried out inﬁnitely slowly. By thermodynamically irreversible one simply means

that one cannot go through the approach–separation cycle via a continuous series

of equilibrium states, because some of these are connected via spontaneous – and

therefore thermodynamically irreversible – instabilities or transitions where energy

is liberated and therefore “lost” via heat or phonon release [268]. This is an area of

much current interest and activity, especially regarding the fundamental molecular

origins of adhesion and friction in polymer and surfactant systems, and the relation-

ships between them [239,259,260,262,264,269–272].

9.6 Introduction: Diﬀerent Modes of Friction and the Limits

of Continuum Models

Most frictional processes occur with the sliding surfaces becoming damaged in one

form or another [263]. This may be referred to as “normal” friction. In the case of

brittle materials, the damaged surfaces slide past each other while separated by rela-

tively large, micron-sized wear particles. With more ductile surfaces, the damage re-

mains localized to nanometer-sized, plastically deformed asperities. Some features

of the friction between damaged surfaces will be described in Sect. 9.7.4.

There are also situations in which sliding can occur between two perfectly

smooth, undamaged surfaces. This may be referred to as “interfacial” sliding or

456 Marina Ruths and Jacob N. Israelachvili

“boundary” friction and is the focus of the following sections. The term “boundary

lubrication” is more commonly used to denote the friction of surfaces that contain

a thin protective lubricating layer such as a surfactant monolayer, but here we shall

use the term more broadly to include any molecularly thin solid, liquid, surfactant,

or polymer ﬁlm.

Experiments have shown that, as a liquid ﬁlm becomes progressively thin-

ner, its physical properties change, at ﬁrst quantitatively and then qualitatively

[44, 47, 273, 274, 276, 277]. The quantitative changes are manifested by an in-

creased viscosity, non-Newtonian ﬂow behavior, and the replacement of nor-

mal melting by a glass transition, but the ﬁlm remains recognizable as a liquid

(Fig. 9.13). In tribology, this regime is commonly known as the “mixed lubrica-

tion” regime, where the rheological properties of a ﬁlm are intermediate between

the bulk and boundary properties. One may also refer to it as the “intermediate”

regime (Table 9.4).

For even thinner ﬁlms, the changes in behavior are more dramatic, resulting in

a qualitative change in properties. Thus ﬁrst-order phase transitions can now occur

to solid or liquid-crystalline phases [46,255, 261,275,278–281], whose properties

can no longer be characterized even qualitatively in terms of bulk or continuum

Velocity u Viscosity

Load

Bound-

ary

Inter-

mediate

(mixed)

Thick film (EHD)

Friction force

~1 nm 2–5 nm ~10 nm ~10 Pm

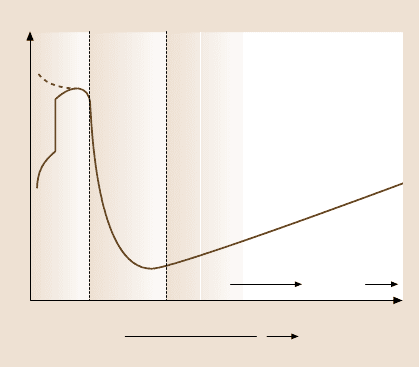
Fig. 9.13. Stribeck curve: an empirical curve giving the trend generally observed in the fric-

tion forces or friction coeﬃcients as a function of sliding velocity, the bulk viscosity of the

lubricating ﬂuid, and the applied load (normal force). The three friction/lubrication regimes

are known as the boundary lubrication regime (see Sect. 9.7), the intermediate or mixed lubri-

cation regime (Sect. 9.8.2), and thick ﬁlm or elasto-hydrodynamic (EHD) lubrication regime

(Sect. 9.8.1). The ﬁlm thicknesses believed to correspond to each of these regimes are also

shown. For thick ﬁlms, the friction force is purely viscous, e.g., Couette ﬂow at low shear

rates, but may become complicated at higher shear rates where EHD deformations of surfaces

can occur during sliding (after [1] with permission)

9 Surface Forces and Nanorheology of Molecularly Thin Films 457

Table 9.4. The three main tribological regimes characterizing the changing properties of li-

quids subjected to increasing conﬁnement between two solid surfaces

Regime Conditionsforgetting

into this regime

Static/equilibrium

properties

Dynamic properties

Bulk

• Thick ﬁlms (> 10

molecular diameters,

 R

for polymers)

• Low or zero loads

• High shear rates

Bulk (continuum)

properties:

• Bulk liquid density

• No long-range order

Bulk (continuum)

properties:

• Newtonian viscosity

• Fast relaxation times

• No glass temperature

• No yield point

• Elastohydrodynamic

lubrication

Intermediate

mixed

• Intermediately thick

ﬁlms(4–10

molecular diameters,

∼ R

for polymers)

• Low loads or

pressure

Modiﬁed ﬂuid

properties include:

• Modiﬁed positional

and orientational order

• Medium- to long-

range molecular

correlations

• Highly entangled

states

Modiﬁed rheological

properties include:

• Non-Newtonian ﬂow

• Glassy states

• Long relaxation times

• Mixed lubrication

Boundary

• Molecularly thin

ﬁlms (< 4 molecular

diameters)

• High loads or

pressure

• Low shear rates

• Smooth surfaces or

asperities

Onset of non-ﬂuidlike

properties:

• Liquid-like to solid-

like phase transitions

• Appearance of new

liquid-crystalline

states

• Epitaxially induced

long-range ordering

Onset of tribological

properties:

• No ﬂow until yield

point or critical shear

stress reached

• Solid-like ﬁlm behav-

ior characterized

by defect diﬀusion,

dislocation motion,

shear melting

• Boundary lubrication

BasedonworkbyGranick [273], Hu and Granick [274], and others [38,261, 275] on the

dynamic properties of short chain molecules such as alkanes and polymer melts conﬁned

between surfaces

Conﬁnement can lead to an increased or decreased order in aﬁlm, depending both on the

surface lattice structure and the geometry of the conﬁning cavity

In each regime both the static and dynamic properties change. The static properties include

the ﬁlm density, the density distribution function, the potential of mean force, and various

positional and orientational order parameters

Dynamic properties include viscosity, viscoelastic constants, and tribological yield points

such as the friction coeﬃcient and critical shear stress

458 Marina Ruths and Jacob N. Israelachvili

liquid properties such as viscosity. These ﬁlms now exhibit yield points (character-

istic of fracture in solids) and their molecular diﬀusion and relaxation times can be

ten orders of magnitude longer than in the bulk liquid or even in ﬁlms that are just

slightly thicker. The three friction regimes are summarized in Table 9.4.

9.7 Relationship Between Adhesion and Friction Between Dry

(Unlubricated and Solid Boundary Lubricated) Surfaces

9.7.1 Amontons’ Law and Deviations from It Due to Adhesion:

The Cobblestone Model

Early theories and mechanisms for the dependence of friction on the applied normal

force or load, L, were developed by da Vinci, Amontons, Coulomb and Euler [282].

For the macroscopic objects investigated, the friction was found to be directly pro-

portional to the load, with no dependence on the contact area. This is described by

the so-called Amontons’ law:

F = μL , (9.26)

where F is the shear or friction force and μ is a constant deﬁned as the coeﬃcient of

friction.This friction law has a broad range of applicability and is still the principal

means of quantitatively describing the friction between surfaces. However, particu-

larly in the case of adhering surfaces, Amontons’ law does not adequately describe

the friction behavior with load, because of the ﬁnite friction force measured at zero

and even negative applied loads.

When a lateral force, or shear stress, is applied to two surfaces in adhesive con-

tact, the surfaces initially remain “pinned” to each other until some critical shear

force is reached. At this point, the surfaces begin to slide past each other either

smoothly or in jerks. The frictional force needed to initiate sliding from rest is

known as the static friction force, denoted by F

, while the force needed to main-

tain smooth sliding is referred to as the kinetic or dynamic friction force, denoted

by F

. In general, F

> F

. Two sliding surfaces may also move in regular jerks,

known as stick–slip sliding, which is discussed in more detail in Sect. 9.8.3. Such

friction forces cannot be described by models used for thick ﬁlms that are viscous

(see Sect. 9.8.1) and, therefore, shear as soon as the smallest shear force is applied.

In Sects. 9.7 and 9.8 we will be concerned mainly with single-asperity contacts.

Experimentally, it has been found that during both smooth and stick–slip sliding at

small ﬁlm thicknesses the local geometry of the contact zone remains largely un-

changed from the static geometry [45]. In an adhesive contact, the contact area as

a function of load is thus generally well described by the JKR equation, (9.22). The

friction force between two molecularly smooth surfaces sliding in adhesive contact

is not simply proportional to the applied load, L, as might be expected from Amon-

tons’ law. There is an additional adhesion contribution that is proportional to the

area of contact, A. Thus, in general, the interfacial friction force of dry, unlubricated

9 Surface Forces and Nanorheology of Molecularly Thin Films 459

surfaces sliding smoothly past each other in adhesive contact is given by

F = F

= S

A+ μL , (9.27)

where S

is the “critical shear stress” (assumed to be constant), A = πr

is the contact

area of radius r given by (9.22), and μ is the coeﬃcient of friction. For low loads we

have:

F = S

A = S

πr

= S





L+ 6πRγ +

12πRγL+

(

6πRγ

)



2/3

;

(9.28)

whereas for high loads (or high μ), or when γ is very low [283–287], (9.27) reduces

to Amontons’ law: F = μL. Depending on whether the friction force in (9.27) is

dominated by the ﬁrst or second term, one may refer to the friction as adhesion-

controlled or load-controlled, respectively.

The following friction model, ﬁrst proposed by Tabor [288] and developed fur-

ther by Sutcliﬀe et al. [289], McClelland [290], and Homola et al. [45], has been

quite successful at explaining the interfacial and boundary friction of two solid

crystalline surfaces sliding past each other in the absence of wear. The surfaces

may be unlubricated, or they may be separated by a monolayer or more of some

boundarylubricant or liquid molecules. In this model, the values of the critical shear

stress S

, and the coeﬃcient of friction μ, in (9.27) are calculated in terms of the

energy needed to overcomethe attractive intermolecularforces and compressive ex-

ternally applied load as one surface is raised and then slid across the molecular-sized

asperities of the other.

This model (variously referred to as the interlocking asperity model, Coulomb

friction,orthecobblestone model) is similar to pushing a cart over a road of cob-

blestones where the cartwheels (which represent the molecules of the upper surface

or ﬁlm) must be made to roll over the cobblestones (representing the molecules of

the lower surface) before the cart can move. In the case of the cart, the downward

force of gravity replaces the attractive intermolecular forces between two material

surfaces. When at rest, the cartwheels ﬁnd grooves between the cobblestones where

they sit in potential-energy minima, and so the cart is at some stable mechanical

equilibrium. A certain lateral force (the “push”) is required to raise the cartwheels

against the force of gravity in order to initiate motion. Motion will continue as long

as the cart is pushed, and rapidly stops once it is no longer pushed. Energy is dis-

sipated by the liberation of heat (phonons, acoustic waves, etc.) every time a wheel

hits the next cobblestone. The cobblestone model is not unlike the Coulomb and

interlocking asperity models of friction [282] except that it is being applied at the

molecular levelandfor a situation wherethe externalload is augmented by attractive

intermolecular forces.

There are thus two contributions to the force pulling two surfaces together:

the externally applied load or pressure, and the (internal) attractive intermolecular

forces that determine the adhesion between the two surfaces. Each of these contri-

butions aﬀects the friction force in a diﬀerent way, which we will discuss in more

detail below.

460 Marina Ruths and Jacob N. Israelachvili

9.7.2 Adhesion Force and Load Contribution to Interfacial Friction

Adhesion Force Contribution

Consider the case of two surfaces sliding past each other, as shown in Fig. 9.14a.

When the two surfaces are initially in adhesive contact, the surface molecules will

adjust themselves to ﬁt snugly together [291], in an analogous manner to the self-

positioning of the cartwheels on the cobblestone road. A small tangential force ap-

plied to one surface will therefore not result in the sliding of that surface relative

to the other. The attractive van der Waals forces between the surfaces must ﬁrst be

overcome by having the surfaces separate by a small amount. To initiate motion, let

the separation between the two surfaces increase by a small amount ΔD, while the

lateral distance moved is Δσ. These two values will be related via the geometry of

the two surface lattices. The energy put into the system by the force F acting over

a lateral distance Δσ is

Input energy: F ×Δσ. (9.29)



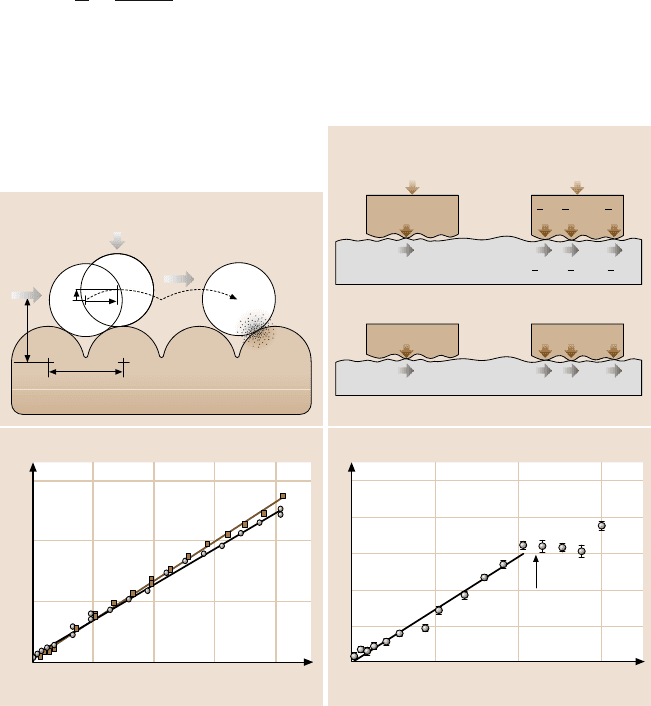
Fig. 9.14. (a) Schematic illustration of how one molecularly smooth surface moves over an-

other when a lateral force F is applied (the “cobblestone model”). As the upper surface moves

laterally by some fraction of the lattice dimension Δσ, it must also move up by some frac-

tion of an atomic or molecular dimension ΔD before it can slide across the lower surface. On

impact, some fraction ε of the kinetic energy is “transmitted” to the lower surface, the rest be-

ing “reﬂected” back to the colliding molecule (upper surface) (after [292], with permission).

(b)Diﬀerence in the local distribution of the total applied external load or normal adhesive

force between load-controlled non-adhering surfaces and adhesion-controlled surfaces. In the

former case, the total friction force F is given eitherby F = μL for one contact point (leftside)

or by F =

μL+

μL = μL for three contact points (right side). Thus the load-controlled

friction is always proportional to the applied load, independently of the number of contacts

and of their geometry. In the case of adhering surfaces, the eﬀective “internal” load is given by

kA,whereA is the real local contact area, which is proportional to the number of intermolec-

ular bonds being made and broken across each single contact point. The total friction force is

now given by F = μkA for one contact point (left side), and F = μ(kA

+ kA

) = μkA

tot

for three contact points (right side). Thus, for adhesion-controlled friction, the friction is

proportional to the real contact area, at least when no additional external load is applied

(c),(d) Friction force between benzyltrichlorosilane monolayers chemically bound to glass

or Si, measured in ethanol (γ<1mJ/m

). (c) SFA measurements where both glass sur-

faces were covered with a monolayer. Circles and squares show two diﬀerent experiments:

one with R = 2.6cm, v = 0.15 µm/s, giving μ = 0.33 ±0.01; the other with R = 1.6cm,

v = 0.5 µm/s, giving μ = 0.30±0.01. (d) Friction force microscopy (FFM) measurements of

a monolayer-functionalized Si tip (R = 11 nm) sliding on a monolayer-covered glass surface

at v = 0.15 µm/s, giving μ = 0.30±0.01. Note the diﬀerent scales in (c)and(d) (after [286],

9 Surface Forces and Nanorheology of Molecularly Thin Films 461

This energy may be equated with the change in interfacial or surface energy as-

sociated with separating the surfaces by ΔD, i.e., from the equilibrium separation

D = D

to D = (D

+ΔD). Since γ ∝ D

−2

for two ﬂat surfaces (cf. Sect. 9.3.1 and

Table 9.2), the energy cost may be approximated by:

Surface energy change×area: 2γA



1−D

/(D

+ΔD)



≈ 4γA(ΔD/D

) , (9.30)

where γ is the surface energy, A the contact area, and D

the surface separation at

equilibrium. During steady-state sliding (kinetic friction), not all of this energy will

be “lost” or absorbed by the lattice every time the surface molecules move by one

lattice spacing: some fractionwill be reﬂected during each impactof the “cartwheel”

molecules [290]. Assuming that a fraction ε of the above surface energy is “lost”

every time the surfaces move across the characteristic length Δσ (Fig. 9.14a), we

obtain after equating (9.29) and (9.30)

4γεΔD

Δσ

. (9.31)

For a typical hydrocarbon or a van der Waals surface, γ ≈ 25mJm

−2

. Other typical

values would be: ΔD ≈ 0.05nm, D

≈ 0.2nm,Δσ ≈0.1nm,andε ≈ 0.1−0.5. Using

Impact

Upper layer (n + 1)

Lower layer (n)

Δσ

ΔD

Load-controlled friction

PkA

Adhesion-controlled friction

Single contact Multiple contacts

Friction force F (mN)

Load L (mN)

40 60 80

SFA

Friction force F (nN)

Load L (nN)

10 15

FFM

Monolayer

transition

462 Marina Ruths and Jacob N. Israelachvili

the aboveparameters,(9.31)predicts S

≈(2.5−12.5)×10

−2

for vander Waals

surfaces. This range of values compares very well with typical experimental values

of 2×10

−2

for hydrocarbon or mica surfaces sliding in air (see Fig. 9.16) or

separated by one molecular layer of cyclohexane [45].

The above model suggests that all interfaces, whether dry or lubricated, dilate

just before they shear or slip. This is a small but important eﬀect: the dilation pro-

vides the crucial extra space needed for the molecules to slide across each other

or ﬂow. This dilation is known to occur in macroscopic systems [293,294] and for

nanoscopic systems it has been computed by Thompson and Robbins [255] and Za-

loj et al. [295] and measured by Dhinojwala et al. [296].

This model may be extended, at least semiquantitatively, to lubricated sliding,

where a thin liquid ﬁlm is present between the surfaces. With an increase in the

number of liquid layers between the surfaces, D

increases while ΔD decreases,

hence the friction force decreases. This is precisely what is observed,but with more

than one liquid layer between two surfaces the situation becomes too complex to

analyze analytically (actually, even with one or no interfacial layers, the calcula-

tion of the fraction of energy dissipated per molecular collision ε is not a simple

matter). Furthermore, even in systems as simple as linear alkanes, interdigitation

and interdiﬀusion have been found to contribute strongly to the properties of the

system [143,297]. Sophisticated modeling based on computer simulations is now

required, as discussed in the following section.

Relation Between Boundary Friction and Adhesion Energy Hysteresis

While the above equations suggest that there is a direct correlation between friction

and adhesion, this is not the case. The correlation is really between friction and ad-

hesion hysteresis, described in Sect. 9.5.4. In the case of friction, this subtle point is

hidden in the factor ε, which is a measure of the amount of energy absorbed (dissi-

pated, transferred, or “lost”) by the lower surface when it is impacted by a molecule

from the upper surface. If ε = 0, all the energy is reﬂected, and there will be no

kinetic friction force or any adhesion hysteresis, but the absolute magnitude of the

adhesion force or energy will remain ﬁnite and unchanged. This is illustrated in

Figs. 9.17 and 9.19.

The following simple model shows how adhesion hysteresis and friction may

be quantitatively related. Let Δγ = γ

−γ

be the adhesion energy hysteresis per

unit area, as measured during a typical loading–unloading cycle (see Figs. 9.17a

and 9.19c,d). Now consider the same two surfaces sliding past each other and as-

sume that frictional energy dissipation occursthrough the same mechanism as adhe-

sion energy dissipation, and that both occur over the same characteristic molecular

length scale σ. Thus, when the two surfaces (of contact area A = πr

)moveadis-

tance σ, equating the frictional energy (F ×σ) to the dissipated adhesion energy

(A×Δγ), we obtain

Friction force: F=

A×Δγ

πr

(

−γ

)

, (9.32)

or Critical shear stress: S

= F/A =Δγ/σ , (9.33)

9 Surface Forces and Nanorheology of Molecularly Thin Films 463

which is the desired expression and has been found to give order-of-magnitude

agreement between measured friction forces and adhesion energy hysteresis [261].

If we equate (9.33) with (9.31), since 4ΔD/(D

Δσ) ≈ 1/σ, we obtain the intuitive

relation

ε =

Δγ

. (9.34)

External Load Contribution to Interfacial Friction

When there is no interfacial adhesion, S

is zero. Thus, in the absence of any adhe-

sive forces between two surfaces, the only “attractive” force that needs to be over-

come for sliding to occur is the externally applied load or pressure, as shown in

Fig. 9.14b.

For a preliminary discussion of this question, it is instructive to compare the

magnitudes of the externally applied pressure to the internal van der Waals pressure

between two smooth surfaces. The internal van der Waals pressure between two ﬂat

surfaces is given (see Table 9.2) by P = A

/6πD

≈ 1GPa(10

atm), using a typical

Hamaker constant of A

= 10

−19

J, and assuming D

≈ 2nm for the equilibrium

interatomic spacing. This implies that we should not expect the externally applied

load to aﬀect the interfacialfriction force F, as deﬁned by (9.27),until the externally

applied pressure L/A begins to exceed ∼ 100MPa (10

atm). This is in agreement

with experimentaldata [298] where the eﬀect of load became dominant at pressures

in excess of 10

atm.

For a more general semiquantitative analysis, again consider the cobblestone

model used to derive (9.31), but now include an additional contribution to the

surface-energy change of (9.30) due to the work done against the external load or

pressure, LΔD = P

ext

AΔD (this is equivalent to the work done against gravity in the

case of a cart being pushed over cobblestones). Thus:

4γεΔD

Δσ

ext

εΔD

Δσ

, (9.35)

which gives the more general relation

= F/A = C

+ C

ext

, (9.36)

where P

ext

= L/A and C

and C

are characteristic of the surfaces and sliding con-

ditions. The constant C

= 4γεΔD/(D

Δσ) depends on the mutual adhesion of the

two surfaces, while both C

and C

= εΔD/Δσ depend on the topography or atomic

bumpiness of the surface groups (Fig. 9.14a). The smoother the surface groups the

smaller the ratio ΔD/Δσ and hence the lower the value of C

. In addition, both C

and C

depend on ε (the fraction of energy dissipated per collision), which depends

on the relative masses of the shearing molecules, the sliding velocity, the temper-

ature, and the characteristic molecular relaxation processes of the surfaces. This is

by far the most diﬃcult parameter to compute, and yet it is the most important since

it represents the energy-transfermechanism in any friction process, and since ε can