Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

444 Marina Ruths and Jacob N. Israelachvili

It is questionable whether the hydration or hydrophobic force should be viewed

as an ordinary type of solvation or structural force that reﬂects the packing of water

molecules. The energy (or entropy) associated with the hydrogen-bondingnetwork,

which extends over a much larger region of space than the molecular correlations,

is probably at the root of the long-range interactions of water. The situation in wa-

ter appears to be governed by much more than the molecular packing eﬀects that

dominate the interactions in simpler liquids.

9.4.5 Polymer-Mediated Forces

Polymers or macromolecules are chain-like molecules consisting of many identical

segments (monomers or repeating units) held together by covalent bonds. The size

of a polymer coil in solution or in the melt is determined by a balance between van

der Waals attraction (and hydrogen bonding,if present) between polymer segments,

andtheentropyofmixing,whichcausesthepolymercoiltoexpand.Inpolymermelts

abovetheglasstransitiontemperature,andatcertainconditionsinsolution,theattrac-

tionbetweenpolymersegmentsisexactlybalancedbytheentropyeﬀect.Thepolymer

solution will thenbehavevirtuallyideally,and thedensitydistributionof segmentsin

the coil is Gaussian. This is called the theta (θ) condition, and it occurs at the theta

or Flory temperature for a particular combination of polymer and solvent or solvent

mixture. At lower temperatures (in a poor or bad solvent), the polymer–polymerin-

teractionsdominateovertheentropic,andthecoilwillshrinkorprecipitate.Athigher

temperatures (good solvent conditions), the polymer coil will be expanded.

High-molecular-weightpolymers form large coils, which signiﬁcantly aﬀect the

properties of a solution even when the total mass of polymer is very low. The radius

of the polymer coil is proportional to the segment length, a, and the number of seg-

ments, n. At thetaconditions,the hydrodynamicradiusof the polymer coil (theroot-

mean-square separation of the ends of one polymer chain) is theoretically given by

= an

1/2

, and the unperturbed radius of gyration (the average root-mean-square

distance of a segment from the center of mass of the molecule) is R

= a (n/6)

1/2

In a good solvent the perturbed size of the polymer coil, the Flory radius R

,is

proportional to n

3/5

Polymers interact with surfaces mainly through van der Waals and electrostatic

interactions. The physisorption of polymers containing only one type of segment

is reversible and highly dynamic, but the rate of exchange of adsorbed chains with

free chains in the solution is low, since the polymer remains bound to the surface

as long as one segment along the chain is adsorbed. The adsorption energy per seg-

ment is on the order of k

T. In a good solvent, the conformation of a polymer on

a surface is very diﬀerent from the coil conformation in bulk solution. Polymers ad-

sorb in “trains”, separated by “loops” extending into solution and dangling “tails”

(the ends of the chain). Compared to adsorption at lower temperatures, good sol-

vent conditions favor more of the polymer chain being in the solvent, where it can

attain its optimum conformation. As a result, the extension of the polymer is longer,

even though the total amount of adsorbed polymer is lower. In a good solvent, the

9 Surface Forces and Nanorheology of Molecularly Thin Films 445

polymer chains can also be eﬀectively repelled from a surface, if the loss in confor-

mational entropy close to the surface is not compensated for by a gain in enthalpy

from adsorption of segments. In this case, there will be a layer of solution (thick-

ness ≈R

) close to the surfaces that is depleted of polymer.

The interaction forces between two surfaces across a polymer solution will de-

pend on whetherthe polymer adsorbsonto the surfacesor is repelled fromthem, and

also on whether the interaction occurs at “true” or “restricted” thermodynamicequi-

librium. At true orfull equilibrium,the polymerbetweenthe surfacescan equilibrate

(exchange) with polymer in the bulk solution at all surface separations. Some theo-

ries [198,199]predict that, at full equilibrium,the polymer chains would movefrom

the conﬁned gap into the bulk solution where they could attain entropically more fa-

vorable conformations, and that a monotonic attraction at all distances would result

from bridging and depletion interactions (which will be discussed below). Other

theories suggest that the interaction at small separations would be ultimately re-

pulsive, since some polymer chains would remain in the gap due to their attractive

interactions with many sites on the surface (enthalpic) – more sites would be avail-

able to the remaining polymer chains if some others desorbed and diﬀused out from

the gap [73,200–202].

At restricted equilibrium, the polymer is kinetically trapped, and the adsorbed

amount is thus constant as the surfaces are brought toward each other,but the chains

can still rearrange on the surfaces and in the gap. Experimentally, the true equilib-

rium situation is very diﬃcult to attain, and most experiments are done at restricted

equilibriumconditions. Even the equilibrationof conformationsassumed in theoret-

ical models for restricted equilibrium conditions can be so slow that this condition

is diﬃcult to reach experimentally.

In systems of adsorbing polymer, bridging of chains from one surface to the

other can give rise to a long-range attraction, since the bridging chains would gain

conformational entropy if the surfaces were closer together. In poor solvents, both

bridging and intersegment interactions contributeto an attraction [26]. However, re-

gardlessof solventand equilibrium conditions,a strong repulsiondue to the osmotic

interactions is seen at small surface separations in systems of adsorbingpolymers at

restricted equilibrium.

In systems containing high concentrations of non-adsorbing polymer, the dif-

ference in solute concentration in the bulk and between the surfaces at separations

smaller than the approximate polymer coil diameter (2R

, i.e., when the polymer

has been squeezed out from the gap between the surfaces) may give rise to an at-

tractive osmotic force (the “depletion attraction”) [207–212]. In addition, if the

polymer coils become initially compressed as the surfaces approach each other, this

can give rise to a repulsion (“depletion stabilization”)at large separations[210]. For

a system of two cylindrical surfaces or radius R, the maximumdepletion force, F

dep

is expected to occur when the surfaces are in contact and is given by multiplying the

446 Marina Ruths and Jacob N. Israelachvili

depletion (osmotic) pressure, P

dep

= ρk

T, by the contact area πr

,wherer is given

by the chord theorem: r

= (2R−R

≈ 2RR

[3]:

dep

/R = −2πR

ρk

T , (9.19)

where ρ is the number density of the polymer in the bulk solution.

If a part of the polymer (typically an end group) is diﬀerent from the rest of

the chain, this part may preferentially adsorb to the surface. End-adsorbed poly-

mer is attached to the surface at only one point, and the extension of the chain is

dependent on the grafting density, i.e., the average distance, s, between adsorbed

end groups on the surface (Fig. 9.8). One distinguishes between diﬀerent regions of

increasing overlap of the chains (stretching) called pancake, mushroom, and brush

Force/Radius F/R (mN/m)

Distance D (nm)

150

–1

–2

50 100

Force/Radius F/R (mN/m)

Distance D (nm)

200

–1

–2

50 100 150

0.10

0.05

–0.05

050100 150 200 250 300

F/R

Time MW= 1.1 × 10

3h 8h > 24h

Distance D (nm)

}

MW = 140,000

MW = 26,000

MW = 1.1 × 10

MW = 1.6× 10

In Out In

a) b)

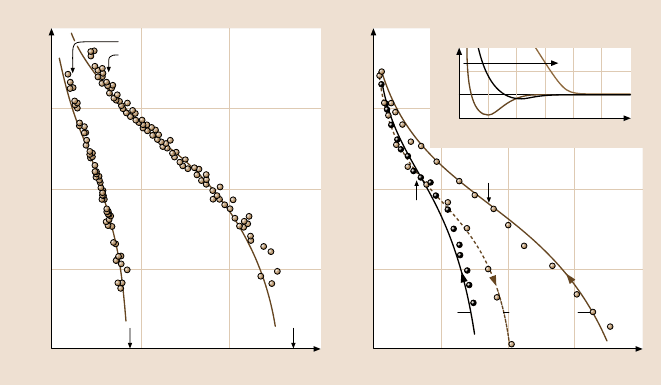
Fig. 9.8a,b. Experimentally determined forces in systems of two interacting polymer layers:

(a) Polystyrene brush layers grafted via an adsorbing chain-end group onto mica surfaces in

toluene (a good solvent for polystyrene). Left curve:MW= 26,000 g/mol, R

= 12 nm. Right

curve:MW= 140,000 g/mol, R

= 32 nm. Both force curves were reversible on approach

and separation. The solid curves are theoretical ﬁts using the Alexander–de Gennes theory

with the following measured parameters: spacing between attachments sites: s = 8.5nm,

brush thickness: L = 22.5 nm and 65 nm, respectively. (adapted from [203]). (b) Polyethy-

lene oxide layers physisorbed onto mica from 150 µg/ml solution in aqueous 0.1 M KNO

(a good solvent for polyethylene oxide). Main ﬁgure: Equilibrium forces at full coverage

after ∼ 16 h adsorption time. Left curve:MW= 160,000 g/mol, R

= 32 nm. Right curve:

MW = 1,100,000 g/mol, R

= 86 nm. Note the hysteresis (irreversibility) on approach and

separation for this physisorbed layer, in contrast to the absence of hysteresis with grafted

chains in case (a). The solid curves are based on a modiﬁed form of the Alexander–de Gennes

theory. Inset in (b): evolution of the forces with the time allowed for the higher MW poly-

mer to adsorb from solution. Note the gradual reduction in the attractive bridging component.

9 Surface Forces and Nanorheology of Molecularly Thin Films 447

regimes [213]. In the mushroom regime, where the coverage is suﬃciently low that

there is no overlap between neighboring chains, the thickness of the adsorbed layer

is proportional to n

1/2

(i.e., to R

) at theta conditions and to n

3/5

in a good solvent.

Several models [213–218] have been developed for the extension and interac-

tions between two brushes (strongly stretched grafted chains). They are based on

a balance between osmotic pressure within the brush layers (uncompressed and

compressed) and the elastic energy of the chains and diﬀer mainly in the assump-

tions of the segment density proﬁle, which can be a step function or parabolic. At

high coverage (in the brush regime), where the chains will avoid overlapping each

other, the thickness of the layer is proportional to n.

Experimentalworkon bothmonodisperse[27,28,203,219]andpolydisperse[30,

220] systems at diﬀerent solvent conditions has conﬁrmed the expected range

and magnitude of the repulsive interactions resulting from compression of densely

packed grafted layers.

9.4.6 Thermal Fluctuation Forces

If a surface is not rigid but very soft or even ﬂuid-like, this can act to smear out

any oscillatory solvation force. This is because the thermal ﬂuctuations of such in-

terfaces make them dynamically “rough” at any instant, even though they may be

perfectly smooth on a time average. The types of surfaces that fall into this category

are ﬂuid-like amphiphilic surfaces of micelles, bilayers, emulsions, soap ﬁlms, etc.,

but also solid colloidal particle surfaces that are coated with surfactant monolayers,

as occurs in lubricating oils, paints, toners, etc.

These thermal ﬂuctuation forces (also called entropic or steric forces) are usu-

ally short range and repulsive and are very eﬀective at stabilizing the attractive van

der Waals forces at some small but ﬁnite separation. This can reduce the adhesion

energy or force by up to three orders of magnitude. It is mainly for this reason that

ﬂuid-like micelles and bilayers, biological membranes, emulsion droplets, or gas

bubbles adhere to each other only very weakly.

Because of their short range it was, and still is, commonly believed that these

forces arise from water orderingor “structuring”eﬀects at surfaces,and that they re-

ﬂect some unique or characteristic property of water. However, it is now known that

these repulsive forces also exist in other liquids [221, 222]. Moreover, they appear

to become stronger with increasing temperature, which is unlikely if the force orig-

inated from molecular ordering eﬀects at surfaces. Recent experiments, theory, and

computer simulations [223–226] have shown that these repulsive forces have an en-

tropic origin arising from the osmotic repulsion between exposed thermally mobile

surface groups once these overlap in a liquid. These phenomena include undulating

and peristaltic forces between membranes or bilayers, and, on the molecular scale,

protrusion and head-groupoverlap forces where the interactions are also inﬂuenced

by hydration forces.

448 Marina Ruths and Jacob N. Israelachvili

9.5 Adhesion and Capillary Forces

9.5.1 Capillary Forces

When considering the adhesion of two solid surfaces or particles in air or in a liquid,

it is easy to overlook or underestimate the important role of capillary forces, i.e.,

forces arising from the Laplace pressure of curved menisci formed by condensation

of a liquid between and around two adhering surfaces (Fig. 9.9).

The adhesion force between a non-deformablespherical particle of radius R and

a ﬂat surface in an inert atmosphere (Fig. 9.9a) is

= 4πRγ

. (9.20)

But in an atmosphere containing a condensable vapor, the expression above is re-

placed by

= 4πR(γ

cosθ + γ

) , (9.21)

where the ﬁrst term is due to the Laplace pressure of the meniscus and the second

is due to the direct adhesion of the two contacting solids within the liquid. Note that

the aboveequation does not containthe radius of curvature,r, of the liquid meniscus

(see Fig. 9.9b). This is because for smaller r the Laplace pressure γ

/r increases,

but the area over which it acts decreasesby the same amount, so the two eﬀects can-

cel out. Experiments with inert liquids, such as hydrocarbons, condensing between

two mica surfaces indicate that (9.21) is valid for values of r as small as 1–2nm,

Configuration

at equilibrium

and pull-off

Equilibrium

JKR

Fig. 9.9a–c. Adhesion and capillaryforces: (a) a non-deforming sphere on a rigid, ﬂat surface

in an inert atmosphere and (b) in a vapor that can “capillary condense” around the contact

zone. At equilibrium, the concave radius, r, of the liquid meniscus is given by the Kelvin

equation. For a concave meniscus to form, the contact angle θ hastobelessthan90

◦

.Inthe

case of hydrophobic surfaces surrounded by water, a vapor cavity can form between the sur-

faces. As long as the surfaces are perfectly smooth, the contribution of the meniscus to the ad-

hesion force is independent of r (after [1] with permission). (c) Elastically deformable sphere

on a rigid ﬂat surface in the absence (Hertz) and presence (JKR) of adhesion ((a)and(c)

9 Surface Forces and Nanorheology of Molecularly Thin Films 449

correspondingto vapor pressures as low as 40% of saturation [148,227,228].Capil-

lary condensationalso occursin binary liquidsystems, e.g.,when waterdissolvedin

hydrocarbon liquids condenses around two contacting hydrophilic surfaces or when

a vapor cavity forms in water around two hydrophobic surfaces. In the case of wa-

ter condensing from vapor or from oil, it also appears that the bulk value of γ

applicable for meniscus radii as small as 2nm.

The capillary condensation of liquids, especially water, from vapor can have

additional eﬀects on the physical state of the contact zone. For example, if the sur-

faces contain ions, these will diﬀuse and build up within the liquid bridge, thereby

changing the chemical composition of the contact zone, as well as inﬂuencing the

adhesion.In the case of surfaces coveredwith surfactant or polymer molecules (am-

phiphilic surfaces),the molecules can turn over on exposureto humid air, so that the

surface nonpolar groups become replaced by polar groups, which renders the sur-

faces hydrophilic. When two such surfaces come into contact, water will condense

around the contact zone and the adhesion force will also be aﬀected – generally

increasing well above the value expected for inert hydrophobic surfaces. It is ap-

parent that adhesion in vapor or a solvent is often largely determined by capillary

forces arisingfrom the condensationof liquidthat maybe present only in very small

quantities, e.g., 10–20% of saturation in the vapor, or 20ppm in the solvent.

9.5.2 Adhesion Mechanics

Two bodies in contact deform as a result of surface forces and/or applied normal

forces. For the simplest case of two interacting elastic spheres (a model that is eas-

ily extended to an elastic sphere interacting with an undeformable surface, or vice

versa) and in the absence of attractive surface forces, the vertical central displace-

ment (compression) was derived by Hertz [229] (Fig. 9.9c). In this model, the dis-

placement and the contact area are equal to zero when no external force (load) is

applied, i.e., at the points of contact and of separation. The contact area A increases

with normal force or load as L

2/3

In systems where attractive surface forces are present between the surfaces, the

deformations are more complicated. Modern theories of the adhesion mechanics

of two contacting solid surfaces are based on the Johnson–Kendall–Roberts (JKR)

theory [15, 230], or on the Derjaguin–Muller–Toporov (DMT) theory [231–233].

The JKR theory is applicable to easily deformable, large bodies with high surface

energy, whereas the DMT theory better describes very small and hard bodies with

low surface energy [234]. The intermediate regime has also been described [235].

In the JKR theory, two spheres of radii R

and R

, bulk elastic modulus K,and

surfaceenergy γ will ﬂatten due to attractivesurface forces when in contactat no ex-

ternalload.Thecontactarea willincreaseunderan externalload L ornormalforce F,

such that at mechanical equilibrium the radius of the contact area, r,isgivenby



F + 6πRγ +

12πRγF + (6πRγ)



, (9.22)

450 Marina Ruths and Jacob N. Israelachvili

where R = R

/(R

+ R

). In the absence of surface energy, γ, equation (9.22) is

reduced to the expression for the radius of the contact area in the Hertz model.

Another important result of the JKR theory gives the adhesion force or “pull-oﬀ”

0 200

D (μm)

100

r (μm)

Undeformed

surface

Surface separation D (nm)

20 120

250

200

150

100

40 60 80 100

Radial distance r (μm)

Surface separation D (nm)

060

250

200

150

100

10 20 30 40

Radial distance r (μm)

–0.5

0.5

x –0.5

0.5

a) b)

L = 0.01N

L = 0.02N

L = 0.05N

Asymptotic

curve at

L = 0.05N

L = 0.21N

R = 1.55cm

0.25°

c) d)

L = –0.005N

L = 0.01N

L = 0.12N

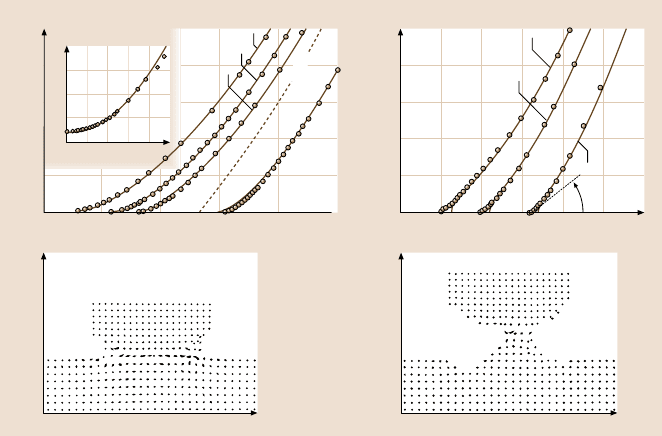
Fig. 9.10a–d. Experimental and computer simulation data on contact mechanics for ideal

Hertz and JKR contacts. (a) Measured proﬁles of surfaces in nonadhesive contact (circles)

compared with Hertz proﬁles (continuous curves). The system was mica surfaces in a con-

centrated KCl solution in which they do not adhere. When not in contact, the surface shape is

accurately described by a sphere of radius R = 1.55 cm (inset). The applied loads were 0.01,

0.02, 0.05, and 0.21 N. The last proﬁle was measured in a diﬀerent region of the surfaces

where the local radius of curvature was 1.45 cm. The Hertz proﬁles correspond to central

displacements of δ = 66.5, 124, 173, and 441 nm. The dashed line shows the shape of the un-

deformed sphere corresponding to the curve at a load of 0.05 N; it ﬁts the experimental points

at larger distances (not shown). (b) Surface proﬁles measured with adhesive contact (mica

surfaces adhering in dry nitrogen gas) at applied loads of −0.005, 0.01, and 0.12 N. The con-

tinuous lines are JKR proﬁles obtained by adjusting the central displacement in each case to

get the best ﬁt to points at larger distances. The values are δ = −4.2, 75.6, and 256 nm. Note

that the scales of this ﬁgure exaggerate the apparent angle at the junction of the surfaces. This

angle, which is insensitive to load, is only about 0.25

◦

.(c)and(d) Molecular dynamics simu-

lation illustrating the formation of a connective neck between an Ni tip (topmost eight layers)

and an Au substrate. The ﬁgures show the atomic conﬁguration in a slice through the system

at indentation (c) and during separation (d). Note the crystalline structure of the neck. Dis-

tances are given in units of x and z,wherex = 1andz = 1 correspond to 6.12 nm. ((a)and(b)

with kind permission from Kluwer Academic Publishers)

9 Surface Forces and Nanorheology of Molecularly Thin Films 451

force:

= −3πRγ

, (9.23)

where the surface energy, γ

, is deﬁned through W = 2γ

,whereW is the reversible

work of adhesion. Note that, according to the JKR theory, a ﬁnite elastic modu-

lus, K, while having an eﬀect on the load–area curve, has no eﬀect on the adhesion

force, an interesting and unexpected result that has nevertheless been veriﬁed exper-

imentally [15,236–238].

Equation (9.22) and (9.23) provide the framework for analyzing results of ad-

hesion measurements (Fig. 9.10) of contacting solids, known as contact mechan-

ics [230,239], and for studying the eﬀects of surface conditions and time on adhe-

sion energy hysteresis (see Sect. 9.5.4).

The JKR theory has been extended [240,241] to consider rigid or elastic sub-

strates separated by thin compliant layers of very diﬀerent elastic moduli, a situation

commonly encountered in SFA and AFM experiments. The deformation of the sys-

tem is thenstrongly dependanton the ratioof r to the thickness of the conﬁnedlayer.

At small r (low L), thedeformationoccurs mostly in the thin conﬁned layer,whereas

at large r (large L), it occurs mainly in the substrates. Because of the changing dis-

tribution of traction across the contact, the adhesion force in a layered system is also

modiﬁed from that of isotropic systems (9.23) so that it is no longer independent of

the elastic moduli.

9.5.3 Eﬀects of Surface Structure, Roughness, and Lattice Mismatch

In a contact between two rough surfaces, the real area of contact varies with the

applied load in a diﬀerent manner than between smooth surfaces [243, 244]. For

non-adhering surfaces exhibiting an exponential distribution of elastically deform-

ing asperities (spherical caps of equal radius), it has been shown that the contact

area for rough surfaces increases approximately linearly with the applied normal

force (load), L, instead of as L

2/3

for smooth surfaces [243]. It has also been shown

that for plastically deforming metal microcontacts the real contact area increases

with load as A ∝ L [245, 246]. In systems with attractive surface forces, there is

a competition between this attraction and repulsive forces arising from compression

of high asperities. As a result, the adhesion in such systems can be very low, espe-

cially if the surfaces are not easily deformed[247–249]. The oppositeis possible for

soft (viscoelastic) surfaces where the real (molecular) contact area might be larger

than for two perfectly smooth surfaces [250]. The size of the real contact area at

a given normal force is also an important issue in studies of nanoscale friction, both

of single-asperity contacts (cf. Sect. 9.7) and of contacts between rough surfaces

(cf. Sect. 9.9.2).

Adhesion forces may also vary depending on the commensurability of the crys-

tallographic lattices of the interacting surfaces. McGuiggan and Israelachvili [251]

measured the adhesion between two mica surfaces as a function of the orientation

(twist angle) of their surface lattices. The forces were measured in air, water, and

452 Marina Ruths and Jacob N. Israelachvili

Adhesion energy E (mJ/m

)

Angle

θ (deg)

–3

–2 –1 0 1 2 3 4 5

170 190

180 θ

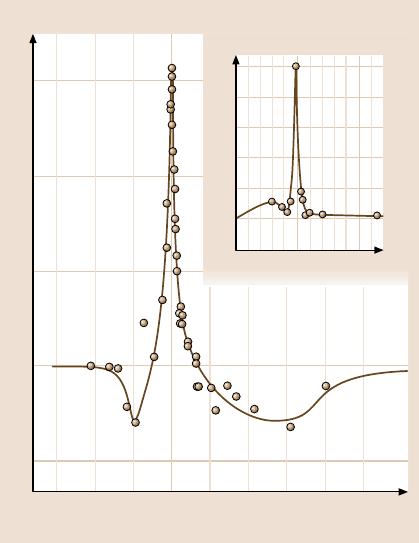
Fig. 9.11. Adhesion energy

for two mica surfaces in con-

tact in water (in the primary

minimum of an oscillatory

force curve) as a function of

the mismatch angle θ about

θ = 0

◦

and 180

◦

between

the mica surface lattices (af-

ter [242] with permission)

an aqueous salt solution where oscillatory structural forces were present. In humid

air, the adhesion was found to be relatively independent of the twist angle θ due to

the adsorption of a 0.4nm thick amorphous layer of organics and water at the inter-

face. In contrast, in water, sharp adhesion peaks (energyminima) occurred at θ = 0

◦

±60

◦

, ±120

◦

and 180

◦

, corresponding to the “coincidence” angles of the surface

lattices (Fig. 9.11). As little as ±1

◦

away from these peaks, the energy decreased

by 50%. In aqueous KCl solution, due to potassium ion adsorption the water be-

tween the surfaces becomes ordered, resulting in an oscillatory force proﬁle where

the adhesive minima occur at discrete separations of about 0.25nm, corresponding

to integral numbers of water layers. The whole interaction potential was now found

to depend on the orientation of the surface lattices, and the eﬀect extended at least

four molecular layers.

It has also been appreciated that the structure of the conﬁning surfaces is just as

important as the nature of the liquid for determining the solvation forces [111,150,

151,252–256]. Between two surfaces that are completely ﬂat but “unstructured”,

the liquid molecules will order into layers, but there will be no lateral ordering

within the layers. In other words, there will be positional ordering normal but not

parallel to the surfaces. If the surfaces have a crystalline (periodic) lattice, this may

induce ordering parallel to the surfaces, as well, and the oscillatory force then also

depends on the structure of the surface lattices. Further, if the two lattices have

9 Surface Forces and Nanorheology of Molecularly Thin Films 453

diﬀerent dimensions(“mismatched” or “incommensurate”lattices ), or if the lattices

are similar but are not in register relative to each other, the oscillatory force law

is further modiﬁed [251, 257] and the tribological properties of the ﬁlm are also

inﬂuenced, as discussed in Sect. 9.9 [257,258].

As shown by the experiments, these eﬀects can alter the magnitude of the adhe-

sive minima found at a given separation within the last one or two nanometers of

a thin ﬁlm by a factor of two. The force barriers (maxima) may also depend on ori-

entation. This could be even more important than the eﬀects on the minima. A high

barrier could prevent two surfaces from coming closer together into a much deeper

adhesive well. Thus the maxima can eﬀectively contribute to determining not only

the ﬁnal separation of two surfaces, but also their ﬁnal adhesion. Such considera-

tions should be particularly important for determining the thickness and strength of

intergranular spaces in ceramics, the adhesion forces between colloidal particles in

concentrated electrolyte solution, and the forces between two surfaces in a crack

containing capillary condensed water.

For surfaces that are randomly rough, oscillatory forces become smoothed out

and disappear altogether,to be replaced by a purelymonotonic solvationforce [134,

150,151]. This occurs even if the liquid molecules themselves are perfectly capa-

ble of ordering into layers. The situation of symmetric liquid molecules conﬁned

between rough surfaces is therefore not unlike that of asymmetric molecules be-

tween smooth surfaces (see Sect. 9.4.3 and Fig. 9.7a). To summarize, for there to

be an oscillatory solvation force, the liquid molecules must be able to be correlated

over a reasonably long range. This requires that both the liquid molecules and the

surfaces have a high degree of order or symmetry. If either is missing, so will the

oscillations. Depending on the size of the molecules to be conﬁned, a roughness

of only a few tenths of a nanometer is often suﬃcient to eliminate any oscillatory

component of the force law [42,150].

9.5.4 Nonequilibrium and Rate-Dependent Interactions: Adhesion Hysteresis

Under ideal conditions the adhesion energy is a well-deﬁned thermodynamic quan-

tity. It is normally denoted by E or W (the work of adhesion) or γ (the surface

tension, where W = 2γ) and gives the reversible work done on bringing two sur-

faces together or the work needed to separate two surfaces from contact. Under

ideal, equilibrium conditions these two quantities are the same, but under most re-

alistic conditions they are not; the work needed to separate two surfaces is always

greater than that originally gained by bringing them together. An understanding of

the molecular mechanisms underlying this phenomenon is essential for understand-

ing many adhesion phenomena, energy dissipation during loading–unloading cy-

cles, contact angle hysteresis, and the molecular mechanisms associated with many

frictional processes.

It is wrong to think that hysteresis arises because of some imperfection in the

system such as rough or chemically heterogeneous surfaces, or because the support-

ing material is viscoelastic. Adhesion hysteresis can arise even between perfectly