Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

280

4 Correspondence of the boundaries

Let us assume that the solution (X, P) of problem (2.6)-(2.8) is sufficiently regular. To

be precise, let us assume that

SUp|Jy| +SUP

L« Q

dJa

+ sup

(J"

P + w(P)|

Y, supp

((.7-TV

{

w(P))

1.1 •- **

(4.1)

<M,

and

« < 1^1 < - in <2 with some e > 0.

(4.2)

The latter condition guarantees that the coordinate transformation is locally invertible

inside Q. Moreover, by virtue of (2.7) in the one-dimensional case this condition means

that the function X(£,t) is monotone increasing as a function of £ whence the bijectivity

of the mapping f i-> X(£, t).

The situation is not that simple in the multidimensional case where the topology of

the set Q(t) may change with time. To establish bijectivity of the mapping Q,(0) i->

Q(t) amounts to proving that X(dQ.(0),t) = dQ(i) for every t > 0. The inclusion

X(dQ,(0),t) C dQ(t) immediately follows from (3.1)-(3.2) because P(£,i) is strictly pos-

itive if £ G O(0) and equals zero for £ G 9fi(0). Let us proceed to prove the inverse inclu-

sion. Take two arbitrary points f,»7 £ 9fi(0), £ ^

T\.

The inclusion dfi(i) c X(dQ(0),t)

follows if X(£, t) ^ X(r], t) for all t €

[0,

T*]

with some T* not depending on £ and

r\.

Let

us take a point £

£ ^-

such that |?y

—

| = 1 and

cos(£-77,77-f„) = 0.

Without loss of generality we may assume that £o = 0. We are going to show that for

every t > 0 small enough

cos(X(^t)-X(ri,t),X(

,t)).

{X{t,t)-X(j,,t),X(r,,t)) 1

\X({,t)-X{ri,t)\\X{ri,t)\ 2'

(4.3)

Inequality (4.3) means that the particles initially located at the points £ and 77 do not

belong to the same ray and, thus, their trajectories cannot hit one another within the

time interval

[0,T*].

Let X(£,t)=Z + Y, X(r],t)=ri + Z, with

= - /

[U"

)*V

P + w(P)](£,T)dr, Z=- r[(J-

)*V

P + w(P)](

,T)dr.

JO ./O

Then for every t > 0

281

(x(£,

x{r,,

t),x(

t)) =

{t-r,

Y-z,r,

= (Z-

,Z)

(n,Y-Z)

(Y-Z,Z).

90(0) is

Lipschitz-continuous, every

two

points £,

80,(0)

can be

connected

by an

arc

L c fi(0) of

length

\L\ < C\£ - n\

with

constant

depending

fi(0).

follows

then

\Y-Z\-

/>-

Z)ds <

\L\

< K

\i -

r,\

with constants

, K\

depending

on C and M.

Thus,

(X&t)

X(r,,t),X(

,t)) <K

\i-

n\, K

const.

the

other hand,

X(£,t) -X(r,,t)

(f-7?) (

-/^£([(

P +

w(P)]

(

,r))

dsdr^j

whence

|X(f,t)-X(r;

)

t)|>|e-»?|(l-/ir3t)

with

constant

depending only

on M, C, N, and

\x(v,t)\

r,- [

[(J-

)*V

w(P)](7

,r)dr

>l-K

(N,M).

Given

M, C, and N, we can

fulfill

(4.3)

claiming that

T* is

sufficiently small:

cos{x(t,t)-xtn,t),x(Ti,t)) =

(X(t,t)-X(

,t),X(ri,t))

\X^t)-X(r,,t)\\X(r,,t)\

\£-n\(l

+ K

T*)

\^ - n\{l - Ktt)

(l-K

~ (1 -

T>)(1

T*)

Theorem

4.1 Let the

solution

(X,P) of

problem (2.6)-(2.8) satisfy conditions

(4.1)

—

(4.2).

If the

boundary

8Q(0) is

Lipschitz-continuous, then there exists

depending

N, M, and dO(0)

such that

(3.1)

establishes

one-to-one correspondence between

Q(0)

and

0(7)

fort

[0,T*].

282

References

[1] J.G.BERRYMAN Evolution

of a

stable profile

for a

class

nonlinear diffusion equa-

tions.

III.

Slow diffusion

on the

line. J.Math.Phys.,

21,

(1980), 1326-1331.

[2]

M.E.GURTIN, R.C.MACCAMY, E.A.SOCOLOVSKY

A coordinate transforma-

tion

for the

porous media equation that renders

the

free-boundary stationary.

Quart.Appl.Math.,

42,

(1984), 345-357.

[3] A.M.MEIRMANOV, V.V.PUKHNACHOV Lagrangian coordinates

in the

Stefan prob-

lem. Dinamika sploshnoy sredy, Novosibirsk,

47,

(1980), 90-111

(in

Russian).

[4]

A.M.MEIRMANOV, V.V.PUKHNACHOV, S.I.SHMAREV

Evolution Equations and

Lagrangian Coordinates, Walter

Gruyter, Berlin, 1997.

[5]

S.I.SHMAREV

Differentiability and analyticity

solutions and interfaces

multidi-

mensional reaction-diffusion equation. Departamento

Matematicas, University

Oviedo, Preprint

n.l,

(2001), 51

pp.

[6]

S.I.SHMAREV, J.L.VAZQUEZ

Lagrangian coordinates

and

regularity

interfaces

reaction-diffusion equations.

C. R.

Acad.

Sci. Paris, Ser.

321, (1994), 993-998.

[7]

S.I.SHMAREV, J.L.VAZQUEZ

On the regularity

interfaces

solutions of reaction-

diffusion equations

via

Lagrangian coordinates. NoDEA,

(1996), 465-497.

The Brezis-Nirenberg problem on H

Existence and Uniqueness of solutions

Silke Stapelkamp

Mathematisches Institut der Universitat Basel,

Rheinsprung 21, CH - 4057 Basel, Switzerland

Email: stapels@math.unibas.ch

Abstract

We consider the equation

AH»U

+ \u + u

= 0 in a domain D' in hyperbolic

space H", n > 3 with Dirichlet boundary conditions. For different values of

search for positive solutions.

Existence holds for

< Ai, where we can compute the value of

exactly if

is a geodesic ball. In particular it turns out that - like in the Euclidean space -

the case n = 3 is different from the case n > 4 and has to be studied separately.

1 Introduction

We consider the problem

»« + Au + u

= 0 in D'

u > 0 in D' (BN)

u = 0 on dD'

where D' is a domain in hyperbolic space H", n > 3, A e R, and 2* = -^ the critical

Sobolovexponent. We want to know for which values of A there exists a solution u €

(D').

The same problem for balls in Euclidean space was solved in 1983 by Brezis and Nirenberg

[BN] and in the following years a lot of extensions of this problem appeared.

In spaces of constant curvature it has been studied by Bandle, Brillard and Flucher [BBF].

The special case of S

has been treated in [BB]. Our aim is now to extend the problem to

domains in hyperbolic space. It turns out that the results are very similar to the results

in the Euclidean case.

After a brief introduction in the hyperbolic space we will discuss the existence of nontrivial

solutions for the two cases n > 4 (section 3) and n = 3 (section 4). In the special case

n = 3 we will make further remarks on properties of solutions.

283

284

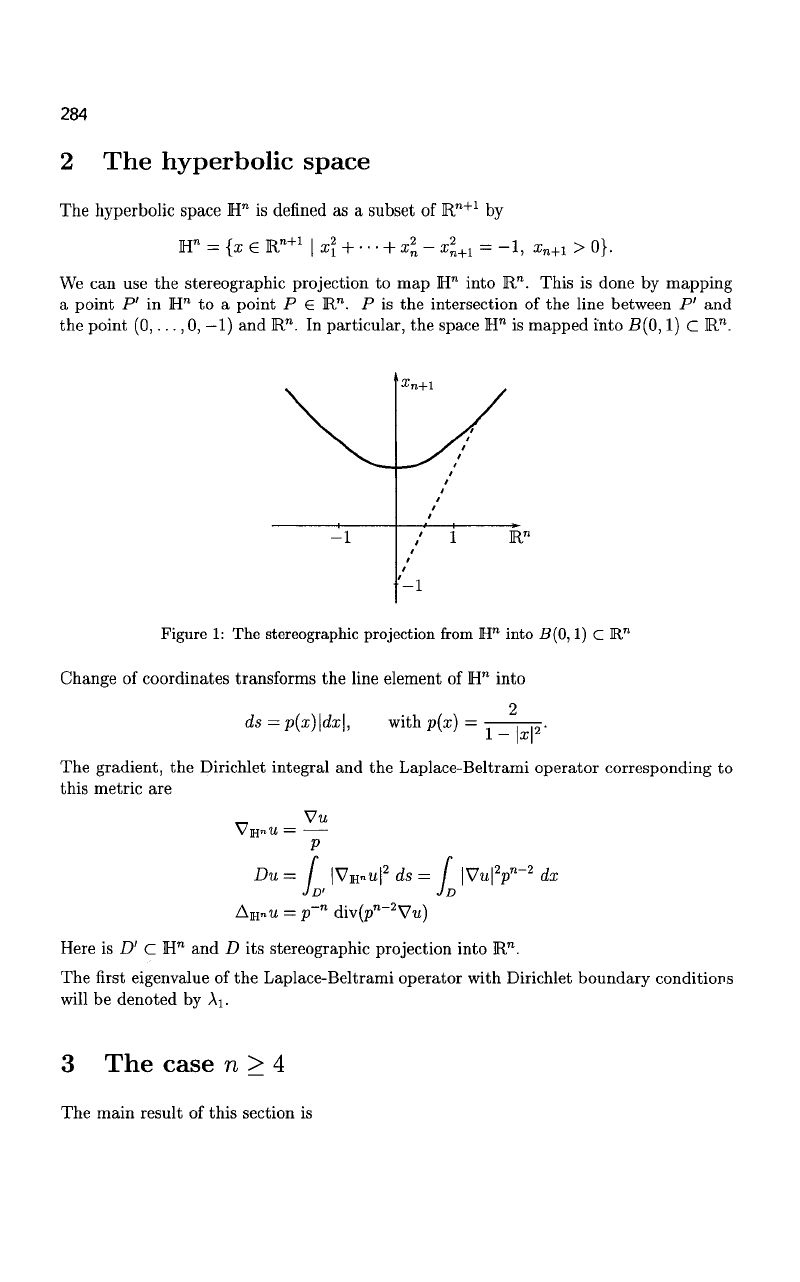
2 The hyperbolic space

The hyperbolic space H

is denned as a subset of R"

= {xe R"

| x\ + • • • +

n+1

= -1, x

n+1

> 0}.

We can use the stereographic projection to map H" into R". This is done by mapping

a point P' in H

to a point P € R". P is the intersection of the line between P' and

the point

(0,...,

0, —1) and

R™.

In particular, the space H

is mapped into B(0,1) C R

Figure 1: The stereographic projection from

H™

into B(0,1) C

R,™

Change of coordinates transforms the line element of H

into

ds = p(x)\dx\, with p(x) ••

± - I^I

The gradient, the Dirichlet integral and the Laplace-Beltrami operator corresponding to

this metric are

»ti = —

Du=

[

-M|

ds= f

|V«|V

-2

»it = p~

div(p"-

Vu)

Here is D' c H

and D its stereographic projection into R

The first eigenvalue of the Laplace-Beltrami operator with Dirichlet boundary conditions

will be denoted by \\.

3 The case n > 4

The main result of this section is

285

Theorem 1 (Existence of solutions for n > 4)

Let D' be a bounded domain in H

,n > 4. Then the following statements are true:

i) For

> Ai the problem (BN) has no nontrivial solution.

ii) For

< "^"

~ ' and if

is starshaped, the problem (BN) has no nontrivial solution.

Hi) If

(

Ai) there exists a nontrivial solution of the problem {BN).

Remarks • Statement i) and ii) of Theorem 1 remain true if n = 3. They can be proved

in the same way.

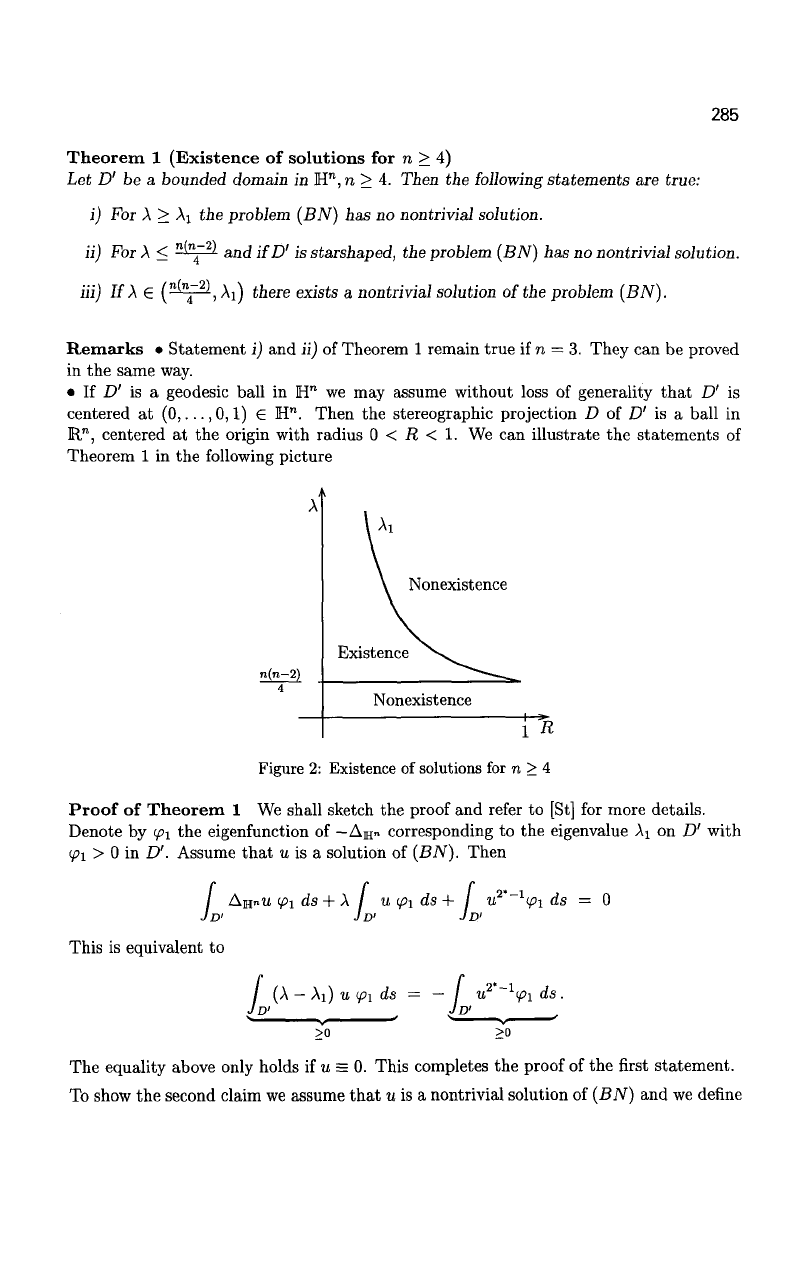
• If D' is a geodesic ball in H

we may assume without loss of generality that D' is

centered at (0, ...,0,1) G H

. Then the stereographic projection D of D' is a ball in

, centered at the origin with radius 0 < R < 1. We can illustrate the statements of

Theorem 1 in the following picture

Nonexistence

Figure 2: Existence of solutions for n > 4

Proof of Theorem 1 We shall sketch the proof and refer to [St] for more details.

Denote by ipi the eigenfunction of

-AH-

corresponding to the eigenvalue Ai on D' with

(pi > 0 in D'. Assume that u is a solution of (BN). Then

/ A

»u ipi ds +

/ u (fi ds + u

Vi ds = 0

JD' J

This is equivalent to

AI)

<pi

- / u

(fi ds.

The equality above only holds if u = 0. This completes the proof of the first statement.

To show the second claim we assume that u is a nontrivial solution of (BN) and we define

286

v(x)

:= f)T~

(x) u(x)

The function v is a nontrivial solution of

A^+(A-"

)

; +

)

= 0 inD

' 2T

' v>0 inZ> (

—^

v = 0 on dD

where D C R" is the stereographic projection of D' into R". Notice that D is also

starshaped.

We now use the classical Pohozaev inequality. Multiplying the equation (BN*) by xVv

we get

(-Av)(xVv) = (v

+ /j,p

v)(xVv)

This equation is equivalent to

-v(Vv(xVv) - x

—^- + x(^ + |pV))

!L^(|V*,|

- v

') - £wV - x\v

Integration over D yields

\L\^

v)dS

=»!y

2)v2dx

Because D is starshaped, the left hand side of the equation is strictly positiv if v is a

nontrivial solution. On the other hand, the right hand side is negativ if

) which

is a contradiction. We conclude that v = 0 in D and u = 0 in D' and the second statement

is proved.

Existence of solutions of problem (BN) will be shown by the concentration-compactness

alternative

([Lil],

[Li2];

for a summary see [B]).

We have to prove that there exists a function u e

(D,pdx)

so that the value of the

quotient

^_J

\Vu\

dx-\f

>P»dxf

is smaller then 5* where 5* denotes the best Sobolev constant of the embedding of

' (D) into

'(D).

As trial functions we choose

, s _n=2, s <p{x)

uAx) =p 2 (x) „_.

287

with

a smooth function,

= l near 0 and

= 0 on dD and estimate the quotient:

QxAc)

~ \S* + 0{e) + c(^21 _

)e\n

E if n = 4

for positive e and with some constant c > 0. We conclude

<2A,P(U

)

< S* if e is small

enough.

In view of the concentration-compactness alternative there exists a minimizer of the quo-

tient if

> "'"

~ ' and this minimizer is a solution of problem {BN) if

< Ai. p.

4 The case n = 3

It turns out that in this case the value of

depends on the geometry of D'. We will give

a complete picture of existence of solutions for geodesic balls. Without loss of generality

we can assume that this ball has his center in (0,0,0,1) G H

Our main result is

Theorem 2 (Existence of solutions for n = 3)

Let D' be a geodesic ball in H

with center at (0,0,0,1), and D = B(0, R) with 0 < R < 1

the stenographic projection of D' into R

. Put

= l + ^-

arctanh R

Then the following statements are true:

i) For

< A* and

> Ai tie probJem {BN) has only the trivial solution.

ii) If

€ (A*,

AI)

there exists a nontriviai solution of the problem {BN).

Proof of Theorem 2 Again we sketch the proof and refer to [St] for details.

The nonexistence results for A > Ai and A < | can be shown in the same way as in the

case n > 4.

To show the nonexistence of a nontriviai solution for | <

we use again a Pohozaev

argument with special test functions.

By the moving plane method we know that if a nontriviai solution exists it is radial.

Problem {BN) is equivalent to

u" + -v! + p

\u +

= 0 in (0, R)

«>0 m{0,R) (BNR)

u{R) = 0

288

Nonexistence

1 R

Figure 3: Existence of solutions for n = 3

Testing the equation (BNR) with r

f(r)u' where

{

sinh(2x/r^T

(r)) • cosh(2

/T^Ag(r)) if f < A < 1

g(r) if

= l

sin(2VA^T

(r)) • cos^y/X^l g{r)) if 1<

< A*

and g(r) = arctanh r

gives us after some computations an integral equality for the solution u which can only

be valid if u = 0. So the first statement is proved.

To prove the second part of Theorem 2 we must again estimate the quotient Q\

. As-

suming

is a smooth function, ip(0) = 1, y'(0) = 0,

<p(R)

= 0 and

we get

with

{x) =

(Ue) =S* +

<p(\x\)

(e +

laf)

(2TT

)

F{tp,\) + 0{e)

i-R

pR pR

F(tp,

A) = 47r / ip'

p dr + 47r / (p

dr -

4TT\

/ ip

dr.

Jo Jo Jo

Now choose ip(r) =

<p\

(r) =

— r

) • cos(7r/2 • arctanh r/arctanh R). This function satisfies

the assumptions above and is a ground state of the eigenvalue problem

-(M)'+PVI-A*PVI

= 0 m{0,R)

ip!>0 in

(0,

(R) = 0, Vi(0) = 0

In particular

/o V>'i Pdr + J

<p\p

/<f

<PiP

= A*

289

and

i-R pR i-R

<p'

dr + (p

dr>\*

I <p

Jo Jo Jo

for all admissible functions

tp.

We deduce

F(y,

> 47r(A* -

and F(ip,

< 0 if

> A*. If e is small enough it follows that

)

< S*. Again we

use the concentration-compactness alternative to conclude that there exists a minimizer

and if

< A

this minimizer is a solution of our problem (BN). —.

Remarks For n = 3 the following properties of nontrivial solutions of the problem (BN)

are known:

• By the moving plane method it can be shown that all solutions of problem BN are

radial and by [KwL] we know that a radially symmetric solution is unique.

• Suppose that u\ is a solution of equation (BN) for

(A*,

Ai).

tends to Ai the solution u> belonging to

tends to 0 pointwise.

tends to A* the radially symmetric solution concentrates at the origin.

(see [B] for references)

• Suppose that D' C H

is a geodesic ball with center at c := (0,0,0,1) e R

and G

is Green's function of An» +

on D' with Dirichlet boundary conditions.

After changing to radial symmetric coordinates in Euclidean space we can compute

G with singularity in 0.

1 1-r

—

cos(4VA

— 1

arctanh R

—

2\/A

— 1

arctanh r)

+ cos(2\/A

— 1

arctanh r)

Denote the regular part of G by h\(r). h\(r) is a monotone decreasing function in r

and is strictly negativ if

< A*. If

> A* the function h\(r) changes sign in (0, R).

In particular h\- (0) = 0.

This supports the conjecture of Budd and Humphries ([BuH], confirm also [B]) as

for balls in S

References

[B] C. Bandle. Sobolev inequalities and quasilinear elliptic boundary value problems. This

volume.