Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

300

S. Agmon, A. Doughs, L. Nirenberg, Estimates near the boundary for solutions of

elliptic partial diffrential equations satisfying general boundary conditions. Comm.

Pure Appl. Math., 12, 1959, 623-727; 17,1964, 35-92.

Benevieri, M. Furi, A simple notion of orientability for Predholm maps of index

zero between Banach manifolds and degree. Annales des Sciences Mathematiques du

Quebec 22 (1998) 131-148.

E.N. Dancer, Boundary-value problems for ordinary differential equations on infinite

intervals. Proc. London Math. Soc. (3) 30 (1975) 76-94

A. Doughs, L. Nirenberg, Interior estimates for elliptic systems of partial differential

equations. Comm. Pure Appl. Math. 8 (1955), 503-538.

K. D. Elworthy, A. J.Tromba, Degree theory on Banach manifolds. Proc. Symp. Pure

Math. AMS (1970) 86-94

C.C. Fenske, Extensio gradus ad quasdam applicationes Fredholmii. Mitt. Math.

Seminar, Giessen, 121 (1976) 65-70.

Fitzpatrick, J. Pejsachowicz, Orientation and the Leray-Schauder theory for fully

nonlinear boundary value problems. Memoirs of the AMS, 1993, 101, No. 483.

V.A. Kondratiev, Boundary value problems for elliptic equations in domains with

conical or angular points. Trudy Moskov. Mat. Obshch. 16 (1967), pp. 209 - 292.

English transl. in: Trans. Math. Soc. 16 (1967).

R.B.

Lockhart, Fredholm property of a class of elliptic operators on non-compact

manifolds. Duke Math. J., 48 (1981), pp. 289 - 312.

J. Mawhin, Topological degree methods in nonlinear boundary value problems. Con-

ference Board of Math. Sciences, AMS, No. 40.

E.M. Mukhamadiev, Normal solvability and the noethericity of elliptic operators in

spaces of functions on R". Part I, Zap. Nauch. Sem. LOMI, 110 (1981), 120-140.

English transl. in J. Soviet Math., 25(1) (1984),

884-901.

S.A. Nazarov, K. Pileckas, On the Fredholm property of the Stokes operator in a

layer-like domain. J. Anal. Appl., 20 (2001), No. 1, pp. 155 - 182.

J. Pejsachowicz, P. Rabier, Degree theory for C

Fredholm mapping of index 0. J.

Anal. Math. 76 (1998) 289 - 319.

Quinn, A. Sard, Hausdorff conullity of critical images of Fredholm maps. Amer.

J. Math. 94 (1972) 1101 - 1110.

301

[15] P. J. Rabier, C. A. Stuart, C^-Fredholm maps and bifurcation for quasilinear elliptic

equations on R

. Recent trends in nonlinear analysis, 249-264, Progr. Nonlinear

Differential Equations Appl, 40, Birkhauser, Basel, 2000.

[16] V. S. Rabinovich, The Fredholm property of general boundary value problems on

noncompact manifolds, and limit operators. (Russian) Dokl. Akad. Nauk 325 (1992),

no.

2,237-241 translation in Russian Acad. Sci. Dokl. Math. 46 (1993), no. 1, 53-58

[17] S. Smale, An infinite dimensional version of Sard's theorem. Amer. J. Math. 87 (1965)

861-866.

[18] A.I. Volpert, V.A. Volpert, Applications of the rotation theory of vector fields to the

study of wave solutions of parabolic equations. Trans. Moscow Math. Soc, 1990, 52,

59-108.

[19] V. Volpert, A. Volpert, J.F. Collet, Topological degree for elliptic operators in un-

bounded cylinders. Adv.

Diff.

Eq., 1999, 4, No. 6, pp. 777-812.

[20] A. Volpert, V. Volpert, Existence of multidimensional travelling waves and systems

of waves. Comm. PDE, 2001, Volume 26, Numbers 3-4, pp. 421 - 459.

[21] H. F. Walker, A Fredholm theory for a class of first-order elliptic partial differential

operators in K". Trans. AMS, 165 (1972), pp. 75 - 86.

[22] V. G. Zvyagin, V. T. Dmitrienko, Properness of nonlinear elliptic differential opera-

tors in Holder spaces. Lecture Notes Math. 1520, Springer-Verlag, Berlin 261-284

Nonlinear diffusion

irregular domains

Ugur G. Abdulla

Max-Planck Institute

for

Mathematics

in the

Sciences

Leipzig 04103, Germany

uabdulla@mis.mpg.de

Abstract

We investigate

the

Dirichlet problem

for the

parabolic equation

= Au

, m >

in a

non-smooth domain

C R^*

> 2. In a

recent paper

[1] (see

also

[2]),

existence

and

boundary regularity results were established

(see

Theorem

2.1 of

[1]).

The

purpose

the present paper

is to

establish uniqueness, comparison

and

stability theorems.

Let

Q be a

bounded open subset

of R^"

, N > 2. Let the

boundary

dQ of Q

consist

the

closure

of an

open domain

lying

in t = 0, an

open domain

lying

= T

G (0, oo)

and a (not

necessarily connected) manifold

lying

in the

strip

0 < t < T.

Denote

Q(T) =

{(x,t)

£ O : t = r} and

assume that

fl(t) ^ 0 for t e

(0,T).

The set

BQ. U

SQ is

called

parabolic boundary

Q. Furthermore

the

class

domains

with described structure will

denoted

2?O,T-

Let Q €

given

and ip be

an arbitrary continuous nonnegative function defined

on VQ- DP

consists

finding

solution

equation

(1) in

DQ,

satisfying

the

initial-boundary condition

on VQ. (2)

We shall follow

the

following notion

weak solutions (super-

subsolutions):

Definition

1.1

We shall say that the function

u is a

solution (resp. super-

subsolution)

(l)-(2),

if :

(a)

u is

nonnegative

and

continuous

locally

Holder continuous

QUDQ, satisfying

(2) (resp. satisfying

(2),

with

replaced

by > or <),

302

303

(b) for any t

, t\ such that 0 < t

< t

< T and for any domain O

t0itl

such

that fiiCflU

DO,

and dBQi, dDQi, SO

being sufficiently smooth manifolds, the

following integral identity holds

/ ufdx= J ufdx+ I (uf

+ u

Af)dxdt- [ u

J-dxdt, (3)

(resp. (3) holds with = replaced by > or <), where f G

Cj*

(Oi) is an arbitrary

function (resp. nonnegative function) which is equal to zero on SOi, and v is the

outward-directed normal vector to Oi(i) at (x,t) G SO^

We shall use the same notation as in [1] : z = (x,t) = (xi,...,x

-1-1

N >2,

x = (x

x) eR

,x = (x

,...,x

) G R"-

, |s|

= Zli\*i\

, m

= £

=2 W

- For a

point z = (x,t) G R^

we denote by B(z;S) an open ball in W

N+1

of radius 6 > 0 and

with center being in z.

Let Q G 2?

,r be a given domain. Assume that for an arbitrary point zo = {x°, t

) G SQ

(or (zo = (z

,0) G SO,) there exist 6 > 0 and a continuous function

such that, after a

suitable rotation of the rc-axes, we have SO

B(z

,6) = {z G

B(ZQ,

: XI =

(f>(x,

t)} and

signal

— <j)(x,t))

= 1 for z G B(z

,i5)

Furthermore, we always suppose in this paper that the conditions of Theorem

2.1 of [1] are satisfied. We are now going to formulate another pointwise restriction

for the point

= (x°,to) G 50, 0 < t

< T, which plays a crucial role in the proof of

uniqueness of the constructed solution. For an arbitrary sufficiently small

> 0, consider

a domain

Q{8) = {(x,t):

|S-z°|

<{8 + t

-t)i,to<t<to + 8}, (4)

Assumption 1.2 Assume for every sufficiently small positive 8, we have

4>{x°,

) -

(j>{x,

t)<[t-t

+ \x-

S°|

for (x, t) G Q{8). (5)

where (i>\ifO<m<l, and /i > ^~ ifm> 1.

Furthermore we denote v

— /i—1

assuming without loss of generality that v G (—1/2,0)

if 0 < m < 1 and v

(-1/ (m +

1),

if m > 1.

Definition 1.3 Let

[c,

(0,

T) be a given segment and SO^ = SO n {(x, t) : c < t <

d}.

We say that assumption 1.2 is satisfied uniformly in [c,d], if there exist

> 0 and

fi> 0 as in (5) such that for 0 < 8 < 8

, (5) is satisfied for all

G SO[

C](

j] with the same

Our main theorems read:

Theorem 1.4 (Uniqueness) Assume that there exists a finite number of points U,

i =

l,...,k

such that t\ = 0 < t

• • •

< t

< i

fc+1

= T and for the arbitrary com-

pact subsegment [<5i,^2] C (*«,t«+i); i = 1,.

• •

,k, assumption 1.2 is uniformly satisfied in

[Si,

82].

Then the solution of the DP is unique.

304

Theorem 1.5 (Comparison) Let u be a solution of DP andg be a super-solution (resp.

sub-solution) of DP. Suppose that the hypothesis of Theorem 1.4 is satisfied. Then u <

(resp. >) g in Q.

Theorem 1.6 (Stability or Li-contraction) Let the assumption of Theorem I.4 be

satisfied. Letgi andg

solutions of DP with initial boundary data

ipi

andip

respectively.

Ifi>i = $2 on SO., then for arbitrary t 6 [0,T] we have

llfll

ff2||t!(n(t))

fIV>X

$21|L,(BO)-

2 Geometric meaning of the assumption

Assumption 1.2 is of geometric nature. To explain its meaning, for simplicity assume

that N = 2, d(zp) = 1 and rewrite (5) as follows: x? - x

< [t - t

+ (x

x^)

}

for (x

,t) G Q{6), where x° =

<j)(x2,t

)

and x

= (p(x2,t) for (x

,t) G Q(S). Consider

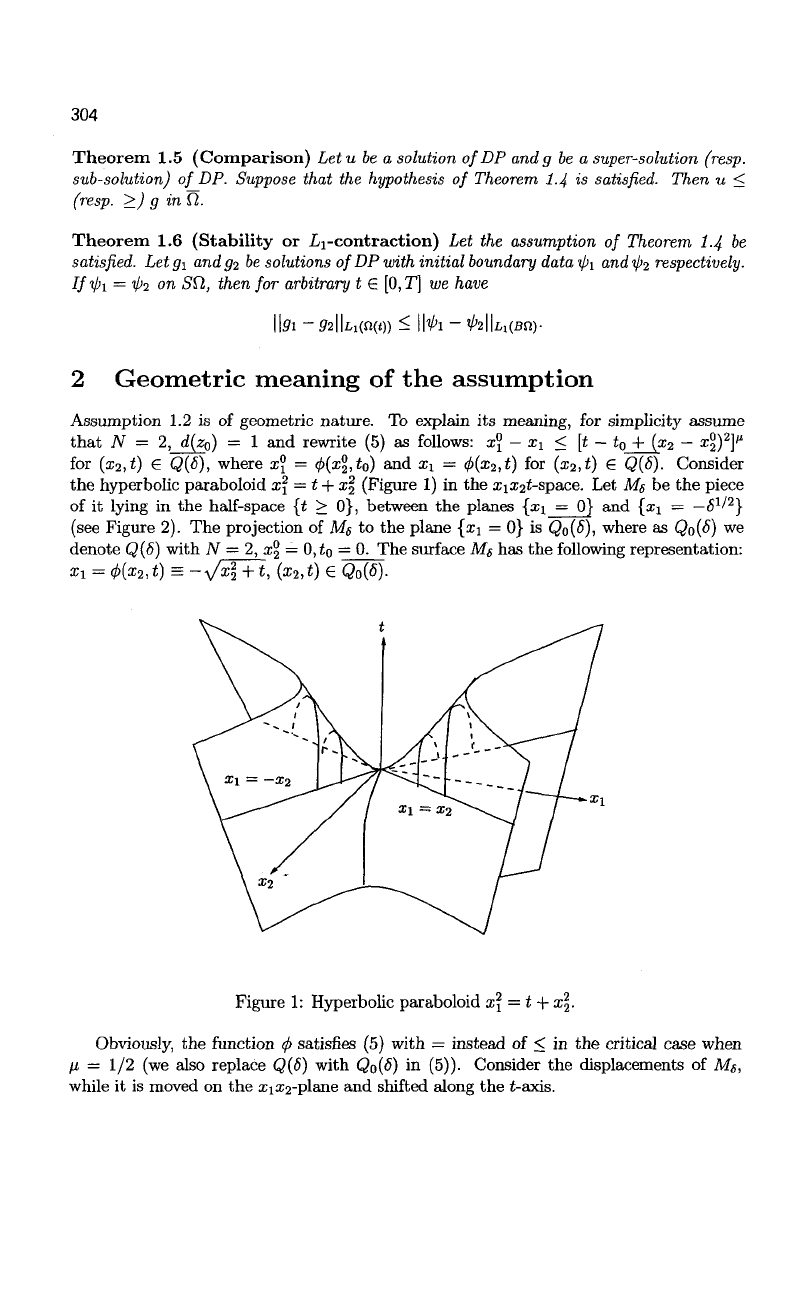
the hyperbolic paraboloid x\ = t + x\ (Figure 1) in the x

t-space. Let Ms be the piece

of it lying in the half-space {t > 0}, between the planes {xi = 0} and {x

= — 5

}

(see Figure 2). The projection of Ms to the plane {xi = 0} is Qo(6), where as Qo(<5) we

denote Q(6) with N

—

2, x° = 0,i

= 0- The surface Ms has the following representation:

Xi = (j){x

,t) = -y/xj+t, (X

,t) € Qo{6).

Figure 1: Hyperbolic paraboloid x\ = t + x\.

Obviously, the function

</>

satisfies (5) with = instead of < in the critical case when

fi = 1/2 (we also replace Q(6) with Qo{6) in (5)). Consider the displacements of Ms,

while it is moved on the xiX2-plane and shifted along the t-axis.

305

II = X2

Xl = -X

Figure 2: Piece Ms of the hyperbolic paraboloid from Figure 1, lying in the half-space

{£ > 0} between the planes {xi = 0} and {xi

—

Let us now consider the critical case of the assumption 1.2 with jx = 1/2. Namely,

we take 1/2 in (5). Equivalent formulation of this critical assumption may be given as

follows: Assume that after the displacement of the above type Ms occupies such a position

that its vertex coincides with the point z

= (x°,t

) G SO,, and for S being positive and

sufficiently small it has no common point with Q.

Similar geometric reformulation of the assumption 1.2 may be given just modifying

the subsurface Ms according to the lower restriction imposed on ft. Thus if 0 < m < 1,

then the exterior touching surface is slightly more regular at the vertex point than related

subsurface Ms of the hyperbolic paraboloid. Otherwise speaking, it is slightly more regular

than G

\ at the vertex point. When m changes from 1 to +oo, the regularity of Ms

increases continuously, for each m being slightly more regular than C£

'"*

at the vertex

point. Another limit position of Ms as m

—•

+oo (or ji

—>

1~) is the upper paraboloid

frustrum with vertex at the origin.

3 Proofs of the main theorems

Proof of Theorem 1.4 Suppose that

and 52 are two solutions of DP. We shall prove

the uniqueness result proving that

51 = g

n {(x, r) : t,- < r <

j+1

l,...,k

(6)

We present the proof of (6) only for the case j = 1. The proof for the cases j =

2,...,

coincides with the proof for the case j = 1. We prove (6) with j = 1, proving that for

306

some limit solution u = limu„, the following inequalities are valid

/ (u(x,t)-gi{x,t))w(x)dx<Q, i = 1,2, (7)

Jn(t)

for every t e (0,t

) and for every

e Cg°(0(i)) such that |w| < 1. Obviously, from (7) it

follows that

<?i

= u =

in f2

{(x,

ti < r <

(8)

which implies (6) with j = 1, in view of continuity of u, gi and g

in fi. Since the proof

of (7) is similar for each i, we shall henceforth let g = g

. Let t G (0,t

) be fixed and let

e Cg

(H(t)) be an arbitrary function such that

\ui\

< 1. To construct the required limit

solution, as in [1], we approximate fi and

i/j

with a sequence of smooth domains il

E X>o,r

and smooth positive functions ip

. We make a slight modification to the construction of

and

ip„.

Let * be a nonnegative and continuous function in

R^"

which coincides

with ip on VQ. This continuation is always possible. Let

i/>

be a sequence of smooth

functions such that

max^n"

) <</>„< (tf

+ Cn""")™,™ =

1,2,...,

(9)

where C > 1 is a fixed constant. For arbitrary subset G C R

N+1

and p > 0, we define

0,(G)=1JS(*,P).

Since g and \]/ are continuous functions in H and g

— if)

on PO, for arbitrary n there

exists p

> 0 such that

(.z) - #

(z)| < n~

for 2 €

(M)

DQ. (10)

We then assume that Q,

satisfies the following:

€

c a

£>n,

o,,„(sn)

(11)

We now formulate assumptions on SQ

near its point z„, which are direct implications

of the assumption 1.2 at the point zo € SCI. Without loss of generality assume that

d(zo) = 1. Assume that S£l

in some neighbourhood of its point z

= (KJ ,s°,i

) is

represented by the function x\ = <p

(x,t), where

{<j>

}

is a sequence of sufficiently smooth

functions and

—»

as n

—>

+co, uniformly in

Q(S

where

> 0 be a sufficiently

small fixed number, which does not depend on n. Obviously, we can assume that

<f>

satisfies assumption 1.2 (namely (5)) at the point (x°,i

), uniformly with respect to n

and with the same exponent p. Let {6

} be some sequence of positive real numbers such

that <5

—»0asn->+oo. Assume also that the sequence

{</>„}

is chosen such that, for n

being large enough, the following inequality is satisfied.

(x°, t

) -

4>n{x,

t) <

- t

+ \x - x°|

] for (x, t) e Q(5

). (12)

Obviously, this is possible in view of the uniform convergence of

<f>

4>.

For example,

if 4>(x,t) coincides with its lower bound 0(x,t) = 0(S°,t

) — [t

—

+ \x

—

x°|

]'',

for

307

(x, t) e Q{6

) (namely (5) is satisfied with = instead of < ), then for all large n such that

< 6

we first choose

<j)

as follows:

^x,t)^> ^,to)-K[t-to + \x-af>\

] for (x,t)€Q(8

4>{x,t) for (x,t)eQ(S

)\Q{6

Obviously,

(j>„

satisfies (12) and converges to

<j>

uniformly in

Q(6Q)-

Then, we easily

construct

(f>

by smoothing

at the boundary points of Q(6

) satisfying t—to+\x—x°\

. In general, we can do similar construction by taking instead of (p

(x,t) the function

(x,

t) =

max(<j>

(x,

t);

<j){x,

t)), which satisfies (12) and converges to

<j>(x,

t)) as n

—>

+00,

uniformly in Q(So). Furthermore we will assume that the sequence 6

is chosen as follows:

^-™-.

r / }\

= n 1+2- with 0 < e < (1 + v)

vlm + -\ +

(13)

where 7 = 1 if m > 1, while if 0 < m < 1 then 7 is chosen such that

i<7<-—• (14)

m vm

Let u

be a classical solution to the following problem:

= Au

, in fi„ U £>O

(15)

u = ip

VSl„.

(16)

This is a nondegenerate parabolic problem and classical theory [3, 4] implies the exis-

tence of a unique C2

-solution. From the maximum principle and (9) it follows that

< u

< M in fi

, n =

1,2,...

(17)

where M is some constant which does not depend on n and M > max(sup

ip,

sup

Pfin

As in [1], we then prove that for some subsequence n', u = linv_

K50

u^ is a solution of

DP (l)-(2). Furthermore, without loss of generality, we write n instead of n'. Take an

arbitrary sequence of real numbers {a/} such that

0 <

< t, a, i 0 as I -> +00. (18)

Let Q

= n„ n

{(X,T)

: a, < T < t}, Q°

= n

{(X,T)

: 0 < T < t},

Sfl

{(X,T)

: a

< T < t}, Sfi° = Sfi

{{X,T)

: 0 < T < t}. Since

M„

is a classical

solution of (15), it satisfies

/ u

fdx= [ u

fdx + [ (u

+u™Af)dxdr- [ u™?fdxdT, (19)

(t) Jnn(ai) Jn'

Jsn'„

for arbitrary / 6

^(Q.

)

which is equal to zero on SQ.

, and where v =

U(X,T)

is the

outward-directed normal vector to fi

(r) at (X,T) e

SQf

Since g is the weak solution of

(l)-(2),

we also have

/ gfdx= [ gfdx+ [ (gf

+ g

Af)dxdT- [ g

^-dxd

. (20)

(t) Jn^at) Jsv

Jsn'

308

Substracting (20) from (19), we derive

(t)(

»-9)f

(

)(

n-9)fdx-

(u^

)^dxdr

+ J

n|i

(un

-gi)[C

+ AnAfldxdr,

where C

1 if m > 1 (accordingly 7

1) and C

= B

if 0

< m

< 1, and

= m

{6uZ

9)g^)

''-

de, B

(forf

6)g^y-

d9.

The functions A, and

are Holder continuous in Q„. From (17) and Definition 1.1

we derive

n^ < A

~A,

n^? < B

for

(a;,

r) e H

(22)

where A,

are some positive constants which do not depend on n. To choose the test

function

/ =

f(x,r) in (21), consider the following problem:

+ A

0 in

ft°

U BQ

(23)

0onSn° and/

w(ai) onfi

(t).

(24)

This

the linear non-degenerate backward-parabolic problem. From the classical

parabolic theory ([3, 4])

follows that there exists

unique classical solution

/„ €

c£'-

1+f,/2

<sZ),

with

some

> 0. From the maximum principle it follows that

l/n|<l inn°.

(25)

By the condition of theorem, assumption 1.2 is satisfied uniformly on every compact

subsegment

(0, i\. We prove that for every fixed

(see (18)) there exists

positive

constant C(l), which does not depend on n, such that

sup \Vf

(z)\<C(l)n

^~\ (26)

To prove (26), we use the modification of the method proposed in [1] for proving the

boundary regularity of the solution to Dirichlet problem. We use (26), in order to estimate

the right-hand side of (21) with

/ =

(x, r), which is a solution of the problem (23)-(24).

We have

f {u

g)iv{x)dx =

-g)fdx-

(u^

)^fdxdr

(27)

(t) Ja

(ai) Jsn

„

Using (9)-(ll), we have

|2b|< sup |V/(z)|

(\iP™-y

\ + \$>

-g

\)dxdT<(C+l)n-

sup |V/(z)|. (28)

z€sn'„ Jsn

z£sn

From (26)-(27), we derive

(C+l)C

(0n'

<1+

(m+7)

(29)

309

where e and 7 are chosen as in (13), (14). Applying (25), we have

|2k|< / \un-g\dx. (30)

•/n„(<*,)

To estimate the right-hand side, we introduce the function

<„\ _ )

"-(

')>

<= ^n(az)

ipn{x,ai),

x e n(a

(

)\fi„(ai).

Obviously v!

(x), x 6 fi(aj) is bounded uniformly with respect to n, I. From (30), we

have

|2i|</ |uJ,-<H«te. (31)

Since linin^+ooW^a:) = u(x, a

) for 2; € n(a(), from Lebesgue's theorem it follows

that

lim / \u'

—

g\dx = / \u(x,ai)

—

g(x,ai)\dx. (32)

Hence, using (28)-(31) in (27) and passing to the limit as n

—»

+00 we have

/ (u

—

g)ui(x)dx < \u

—

g\dx. (33)

Jn(t) Jn(ai)

Let

Obviously, [/; is uniformly bounded with respect to I. Hence, from (33) we derive that

/ {u - g)u(x)dx < \Ui(x)\dx + C

meas(n(ai)\BQ,), (34)

where the constant C

does not depend on I. Prom Lebesgue's theorem it follows that

lim / |[/,(x)|dx = 0.

+°° J

Hence, passing to the limit as / —• +00, from (34), (7) follows. As it was explained

earlier, from (7), (6), with j = 1 follows. Similarly, we prove (6) (step by step) for each

j =

2,...,

k. Theorem 1.4 is proved. The proofs of the Theorems 1.5 and 1.6 are similar

to the given

proof.

References

[1] U.G. Abdulla, On the Dirichlet problem for the nonlinear diffusion equation in non-

smooth domains. J. Math. Anal. Appl. 260(2) (2001), 384-403.

309