Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001

Подождите немного. Документ загружается.

260

We give two examples of domains in R

, which are not star-shaped but conformally

contractible, and the associated vector-field £ satisfies div£ < 0.

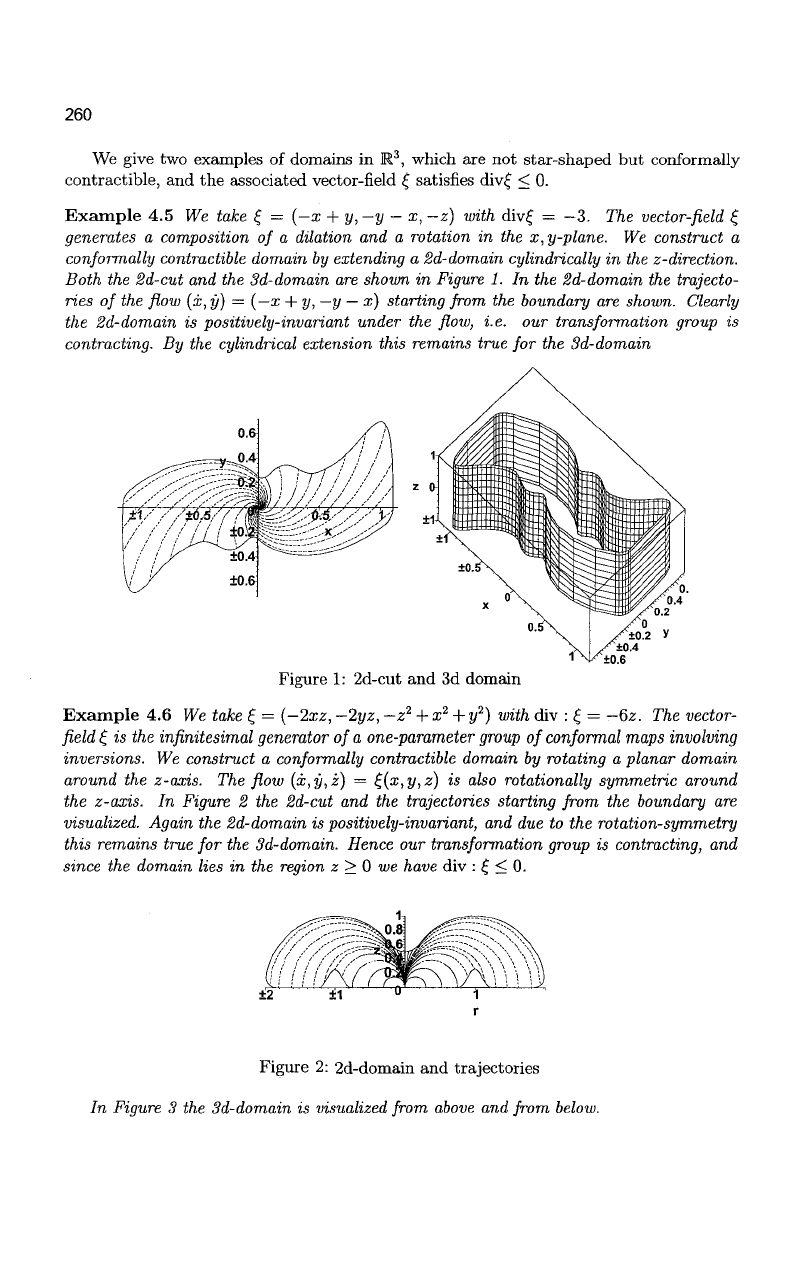
Example 4.5 We take £ = (—x + y, — y

—

x, —z) with div£ = —3. The vector-field £

generates a composition of a dilation and a rotation in the x, y-plane. We construct a

conformally contractible domain by extending a Sd-domain cylindrically in the z-direction.

Both the 8d-cut and the 3d-domain are shown in Figure 1. In the 2d-domain the trajecto-

ries of the flow {x, y) = (—a; + y,

—y —

x) starting from the boundary are shown. Clearly

the 2d-domain is positively-invariant under the flow, i.e. our transformation group is

contracting. By the cylindrical extension this remains true for the Sd-domain

Figure 1: 2d-cut and 3d domain

Example 4.6 We take £ = (—2xz, — 2yz, —z

+ x

+ y

) with div : £ = —6z. The vector-

field £ is the infinitesimal generator of

one-parameter

group

of conformal maps involving

inversions. We construct a conformally contractible domain by rotating a planar domain

around the z-axis. The flow (x,y,z) = £(x,y,z) is also rotationally symmetric around

the z-axis. In Figure 2 the 2d-cut and the trajectories starting from the boundary are

visualized. Again the 2d-domain is positively-invariant, and due to the rotation-symmetry

this remains true for the 3d-domain. Hence our transformation group is contracting, and

since the domain lies in the region z > 0 we have div : £ < 0.

Figure 2: 2d-domain and trajectories

In Figure 3 the 3d-domain is visualized from above and from below.

261

Figure 3: 3d-domain from above and below

4.2 A problem of Brezis and Nirenberg

In a famous paper [1], Brezis and Nirenberg showed that the problem

Au + \u + u

= 0 in Bi(0) Cl

, u = 0 on 9Bi(0),

has a positive solution precisely for A £ (n

/i,n

). The fact that no positive solution

exists for A < 0 follows from Theorem 4.3. The non-existence for A 6 [0,7r

/4] was

found by Brezis and Nirenberg via a Pohozaev-type identity. We indicate how this result

follows by the method of transformation groups. Since all positive solutions are radially

symmetric, a corresponding functional

C[u]

= J

L(r, u, u') dr has Lagrangian L(r, u, u') =

{\\u'\

—

- |u

. It turns out that for

> 0 the dynamical system

r = - sin(2v

Ar), u = I

' - 7Acos(2v

Ar)

generates a transformation-half group which can be shown to be a variational sub-symme-

try for the functional C by using Proposition 3.2 and (5). However, the half-group is

contracting if and only if f < 0, i.e. if and only if sin(2\/Ar) > 0, which restricts

to the

interval

[0,

/4].

Uniqueness of the zero-solution for such values of

is then obtained by

Theorem 3.3.

4.3 Further applications

In our forthcoming work [5] we have included many applications of the interaction of

one-parameter transformations groups and variational problems. We end this paper with

a list of interesting applications which can be treated by our method.

(1) For vector variational problems §

L{x,u

,... ,u

,Vu

)dx Theorem 3.3 will

hold provided L(x, 0,..., 0,

,...,

) is rank-one convex.

(2) For m-Laplace problems div : (\Vu\

Vu) + |u|

p-1

« = 0 in fi with u = 0 on

dQ. and p > -^ 1 uniqueness of the zero-solution will hold for conformally

contractible domains, where up to a constant shift the associated vector-field f is

a linear combination of vector-fields X and

from Lemma 4.1. In particular the

domain of Example 1 is included.

262

(3) For the fourth-order problem A

u = |u|

p_1

u in Q with u = Vu = 0 on dfl the same

class of conformally contractible domains as in Theorem 4.3 gives rise to uniqueness

of the zero-solution provided p > ~^.

(4) Schaaf [6] proved uniqueness results in a different class of domains for exponents

P ^

Pc,

where p

is larger then the critical Sobolev-exponent.

References

[1] H. Brezis and L. Nirenberg, Positive solutions of nonlinear elliptic equations involving

critical Sobolev exponents. Comm. Pure Appl. Math. 36 (1983), 437-477.

[2] P.J. Olver, Applications of Lie Groups to Differential Equations. Graduate Texts in

Mathematics 107, Springer-Verlag, Berlin, 1986.

[3] S.I. Pohozaev, Eigenfunctions of the equation Au + \f(u) = 0. Soviet Math. Dokl 6

(1965),

1408-1411. English translation, Dokl. Akad. Nauk. SSSR 165 (1965), 33-36.

[4] P. Pucci and J. Serrin, A general variational identity. Indiana Univ. Math. J. 35

(1986),

681-703.

[5] W. Reichel, Uniqueness theorems for variational problems by the method of transfor-

mation groups. In preparation.

[6] R.

Schaaf,

Uniqueness for semilinear elliptic problems - supercritical growth and do-

main geometry. Advances in Differential Equations 5 (2000), 1201-1220.

[7] R.C.A.M. Van der Vorst, Variational identities and applications to differential systems.

Arch. Rational Mech. Anal. 116 (1992), 375-398.

[8] A. Wagner, Pohozaev's identity from a variational viewpoint. Z. Anal. Anwendungen,

to appear.

Structure of the solution flow for steady-state

problems of one-dimensional Fremond models of shape

memory alloys

Ken Shirakawa

Department of Mathematics,

Faculty of Education, Chiba University,

1-33 Yayoi-cho, Inage-ku,

Chiba, 263-8522, Japan.

Email: shirakaw@math.e.chiba-u.ac.jp

Abstract

In this paper, we consider a steady-state problem of one-dimensional Fremond

model of shape memory alloys. Recently, the detailed structure of steady-state

solutions has been studied in [12]. According to the result, we see a sudden change of

solution sets at the critical temperature. The main objective of this paper is to give

more detailed information for the variation of solution sets with respect to (steady-

state) temperature. More precisely, we shall characterize the variation of solution

sets by Hausdorff distance between any steady-state solution at a temperature and

any solution set at another temperature.

1 Introduction

This work is motivated by the following one-dimensional mathematical model of shape

memory alloys, of the form:

' M - L

i)t + ((<»(*) - 0°?W))X2Ux)t ~ hti

Oi{d)

a.e. in Q := (0, +00) x (0,1),

a = u

+ /3a(i9)x2, o

= 0, a.e. in Q,

(xi\ ,a

/»V

, , .

(HP-o)\

•

_ A

7T~2 +

Mxi> X2) 2> , a.e. in Q,

< dt\

2j dx

\x2j \-a{ti)u

J (

)

{t, 0) - k(d(t, 0) - $) = hd

{t, 1) + k{d{t, 1) - 1?) = 0, a.e. t > 0,

u(t,Q) = 0, a(t, 1) = Pg(t), a.e. t > 0,

(Xi)x(t, 0) = (Xi)x(t, 1) = 0, a.e. t > 0, i = 1,2,

. 0(0, •) = ^o, Xi(0, •) = xtfi, « = 1,2, a.e. x G (0,1).

263

264

(1.1) is proposed by Fremond (cf. [4, 7, 8, 9]), and the well-posedness for solutions of

(1.1) is studied by many mathematicians from various viewpoints (cf. [1, 2, 6, 10, 11]).

In this model, the phenomena of shape memory alloys are interpreted as a solid-solid

phase transition among three phases: the austenite and two kinds of martensites. In

the context, there are five variables: the absolute temperature $, the one-dimensional

longitudinal displacement u, the stress a, and two order parameters xi

d X2 relative

to local proportions of martensites. More precisely, xi and Xi

are

defined by the sum of

local proportions of two martensites and difference between them, respectively. Then, the

pair (xi(t,x),X2(t, x)) is always on the following closed triangle K in K

, of the form:

K := { fori) € E

| 0 < £ < 1, -( < rj < £ } ; (1.2)

for any (t,x) G Q. IK is the indicator function on the closed triangle K, and dI

the subdifferential of IK, which is a maximal monotone in R

. i9* > 0 is the critical

temperature, a : [0, +oo) —y R is a smooth function with the derivative a! such that:

for a certain large constant d

> d*,

a >

a' < 0 on

[0,

) and a = a' = 0 on

[i9

+00).

g is a smooth function with respect to t such that g(t)

—•

0 as t

—>

+00. $, c

, L, h, k, j3,

(j,,

A and I are positive constants.

Supposing that a is very small and

&o,

X;,o G H

^, 1), i = 1, 2, the large time behavior

for solutions of (1.1) was studied by Colli-Laurengot-Stefanelli (cf. [5]). According to their

result,

i?(t) -> fl and a(t)

—•

0 in appropriate senses as t

—>

+00, respectively.

Therefore, putting "{($) := /3a(^)

, the steady-state problem for (1.1) is essentially a

boundary value problem of the following vector-valued equation, of the form:

[ (xf)x(0) = (xf),(l) = 0, i = l,2;

since the displacement «* in the steady-state can be calculated by

(x) = -f)a{ti) f xt(y) dy for all x € (0,1).

Recently, the detailed structure of solutions {X11X2} (steady-state solutions) of (Py

is studied in [12]. According to the result, solution sets in cases of 0 <$<$*,$ = i9*,

•d*

< $ < §

and i5

< d have quite different profiles. It implies that the physical situation

changes dramatically at two characteristic temperatures

1?*

and $

Now we would like to observe the variation of solution sets with respect to $, more

precisely. In other words, our interest is the structure of the flow of solution sets with

respect to $. In this paper, we shall characterize the variation by a new concept, named

"arcwise-connectable". Namely, a steady-state solution at a temperature tf is called

265

arcwise-connectable, if the Hausdorff distance between the solution and any solution set

at $ / d converges to 0 as d -» d. By making use of the concept, we shall discuss about

the structure of the flow of solution sets with respect to $.

Consequently, more detailed information of the variation of physical situations with

respect to steady-state temperature will be observed.

Notation 1.1 (Hausdorff distance) Let X be a real Banach space. In this paper we

denote by |

•

\x the norm of X, and define the distance between any point a £ X and any

subset BcXby distx(a, B) := inf \x

—

a\x-

xEB

2 Structure result for steady-state solutions

Let $ be any (fixed) positive constant. In this section, we recall the structure result

for solutions of (-P)'', which is obtained in [12].

Definition 2.1 A pair (

^ ) of functions xt, i =

2, on [0,1] is called a solution of

{P)®, if xt e

(0,1),

(xf)x(O) = (xf)x(l) = 0, i = 1,2, and there exist two functions

£f € L

(0,1), i = l,2, such that

OM*!,xt)»d-4(«f)

(J)

-(•£,>i

MM).

In order to describe the structure result smoothly, we introduce the following notation.

Definition 2.2 Let T :=

[T~*,T*]

be any compact interval in R with r„ < r*, n > 0, and

r, < r < T*. For any nonnegative integer n, we define a subclass Sr(ft,r;n) in H

(0,1)

as follows.

(I) S

(K,T;0) :=

{n,T,r*}.

(II) For n > 1, x €

ST(K, T;

n), if and only if there exist a constant c

e R, a partition

—S/KIT

Xi0

< ••• < x

< ••• <

XiH

XiJl+1

:= 1

such that: putting J

X:k

,k,

Xik

\/K7I"), A;

= 1,

• •

•, n,

(i) |c

| < min{T*-r,r-T»};

(ii)

Xtk

+ i/K7r <

x>t+

for k = 0,1,

• •

•, n;

(iii) if |c

| < min{r*

—

T,T

— T»},

then x^.^ + I/KK = x

,k+i, fc = 0,1,

•

•, n;

in other words, if x

+ \[KK <

Xtk+

for some 0 < k < n, then c

min{r*

—

T,T

—

T*},

and \ =

* or x =

the corresponding interval

+ x/K7r,a;t

i];

(iv) x{x) = (-l)

fc_1

cos ( -j^- J +

for z e

k = 1,

• •

•, n.

266

Remark 2.1 Since

,k\

—

S/KK

for any

we notice that

n*(«) := sup

{

(K,

r; n)

} <

+oo.

(2.1)

"*(")

In fact, since n*(K)y/Kir

= V^

\Jxk\

1) we have

0 <

n*(/c)

< _ <

+oo.

fe?

K7r

Let us define

{r*},

if T

<T„

{K,T)

:= • \J

(K,r;n),

if r. < r < r*, (2.2)

71=0

{r,},

T>r*.

Then, according

results

Chen-Elliott [3],

"ST(K,

and only

if x is a

solution

of the following boundary value problem:

-K-XXX

+ 9I

{x) 3 X-T a.e. in (0,1),

Xx(0)

x*(l)

where

dlr is

the subdifferential of the indicator function on the closed interval

Now the structure result

for

solutions

(P)*

stated

follows.

Proposition 2.1 (Structure of solutions of (P)*J Let Kn,

K\, K

and

be subsets of

the boundary

of the triangle

(1.2),

defined by:

{(0,0), (1,1),

(1,

-1)} ,

K, ~ {

(£,

r,)

dK | £ =

1 }

:={(t,rj)edK\Z

= Ti} and K.

{

(£,,,)

dK | £ = -,,

}

respectively. Then, a pair (

) is a

solution

(P)*,

and onty

if;

(si^

fi/ie case ofQ<ti<d*) (x*, X*)

^i °"

[°> *]>

"«meli/ x?

[0,1],

and

is in

the class £[-i,i] I -A-,0

(s2) (the case

of'

$*,)

xi =

const, on

[0,1],

and

the class S[-i,i]

-V, 0

(sS) (the case of

•&*

< ti < tf

)

(x?,xf)

UK_ on

[0,1],

namely |xf

x! on

[0,1],

and x?

is in

the class

Sin

-^4-,

' ~. '

in particular,

if ~_ ' > 1,

i/ien x?

= 0

[0>

1]/

(tyj (the case of $

> ti

) xf =

= 0

[0,1].

267

3 Statement of the main result

(0,1)

Throughout this paper, let us denote by W the product space x . Here we define

(0,l)

S[d) := | (

\) e W (

\ is a solution of {P)

j for any tf > 0.

Then we see from Proposition 2.1 that S(d) is nonempty for any # > 0, and profiles

of S(d) in cases of 0 < d <

•d*,

d =

•d*,

tf*

< 0 < tf

and tf > tf

_are quite different

Now, the objective of this section is to investigate the variation of S{d) with respect to t?

more precisely. In order to characterize the variation of S(d), we introduce the following

concept.

Definition 3.1 (Arcwise-connectable) Let d be any positive constant, and x'

'•—

(

- ]

be any solution of (P)*. Let distw(-, •) be the Hausdorff distance as in Notation 1.1 with

X = W. Then:

(i) x

called above (resp. below) arcwise-connectable at d, if

dist

, S{f)) ->• 0 as 0 \ d (resp. tf />)?);

(ii) x"* is called arcwise-connectable at tf, if it is above arcwise-connectable and below

arcwise-connectable;

(iii) x* is called arcwise-disconnectable at

if it is neither above arcwise-connectable

nor below arcwise-connectable.

Remark 3.1 Based on the concept as the above definition, we have some informations

concerned with the variation of solution sets. For example, if S(fl) includes a lot of

arcwise-disconnectable solutions, then we can imagine a sudden change of solution sets

at d > 0. On the other hand, if there are many arcwise-connectable solutions in S{5) at

•§

> 0, then it implies that S(-) does not vary so suddenly in a neighborhood of d.

Remark 3.2 Let us assume that i9* < d < ?9

with Mz^l > l, or ?9 > i?

. Then, we

7(«)

easily see from Proposition 2.1 that all solutions are arcwise-connectable, because they

are constants on

[0,1].

Therefore, in the rest of this paper, we consider only the case of

0 < tf < tf

with ^p < 1.

Now, our main result is stated as follows.

Theorem 3.1 Let K

, K\, K

and K- be the same as in

(2.3).

(A) A solution I

\ ) € S{d) is above arcwise-connectable, if and only if:

(al) (the case ofO < d <

•&*)

(supp (xf)z)

+ 0;

(a2) (the case of

= 0*) (xf.xf) ^ K

[0,1];

268

(aS) (the case of 0 <

-&4^ < 1 )

xf = const, on [0,1] or 0 ± (supp (xf)*)

C (xf)"

(0);

(WJ (the case of\< ^T

< 1 )

xf = const, on [0,1] or 0 / (supp (

f)*)

c (xf

(l)-

fB) 4 solution I

-\ e S(d) is below arcwise-connectable, if and only if:

(bl) (the case o/

< i9 <

?9*

Xf = const, on [0,1] or (xf ^(l) U (xf)"

(-1) ± 0;

f&2j fifce case o/tf =

•&*)

(xf,xf) £

[°> *]

s«cfc iftat

Xf = const, on [0,1] or (xf)"

!!) U (xf)"

!-!) ^ 0/

(63J (Ue case o/O < ^y^ < ± J

X? = const, on [0,1] or (supp (

f)*)

C (xf)-

(0) * 0;

(H) (tte case of \ <

-&4^- < 1 )

xf = const on [0,1] or (supp (xf

)*)

C CJcf)

(l) # 0-

Remark 3.3 Noting the case of $ = i?*, we see that all steady-state solutions are arcwise-

disconnectable except for constant solutions. It implies that the physical situation changes

dramatically at the critical temperature $*.

4 Proof of the main theorem

In this section, we give the proof of Theorem 3.1. Let 5r(«, r) be the class as in (2.2)

for any compact interval T :=

[i"*,''"*],

K > 0 and T 6 K, and let dist

i)(-, •) be the

Hausdorff distance as in Notation 1.1 with X = £

(0,1). Here, for the proof of Theorem

3.1,

we prepare some lemmas.

Lemma 4.1 Let d > 0, x £ L

(0,1), T :=

[T,,T*]

be any compact interval in R and

< f <

O —> (0, +00) be

a continuous and strictly increasing function. Then:

(i) dist

0jl

)(x,

ST(K(I9), T)) —>

0 as $ \ d if and only if

xeS

(k,(i)),f) such that (supp x*)

^ 0; (4.1)

(ii) dist£2(

)(x, Sr(/«($),f))

—>

0 as

/* $ if and only if

xeS

(k{d),f) suchthat x=const. on[Q,l\orx~

{r*)\Jx~

)j=%. (4.2)

269

Proof.

First,

let us

assume that dist/,2(

)(x,

(K,(IL)),T)) —>

0 as d \

•&

(resp.

•$

/•

•&).

Then

find sequences

{pj\ C 0 and Xj £

ST(K($

)

),T),

j > 1,

such that

inf

K(I?J)

> 0, fy \ tf (resp. ^ /> tf),

K(^)

K(I?)

(resp. «($,) />

K(I?)),

(4.3)

3>i

and

—•

(0,1)

as j ->

+oo.

(4.4)

(4.3) and

Remark 2.1,

sup n*(«(#,))

< +oo,

where n*(/c(i9,))

is the

number

as in (2.1)

with

K($J).

Therefore taking

subsequence

if necessary,

find

integer

0 < n < n*

such that

Xj £

ST(K(I?J),

f; n) for all j > 1.

n = 0,

then

follows from

(I)

of Definition 2.2, (4.3)

and

(4.4) that

x £

ST(K(^),

°)>

namely

(4.1)

(resp. (4.2)) holds.

n > 1,

then

we see

from

(II)

Definition

2.2

that

for

any

j > 1,

(-l)*c

for

,fc+

/«;(^-)'

xj,*+i]' &

0,1,

•

• •

,n,

(-l)

fc_1

. cos

—-7==-

I +

for x

G J

Xjtk

k =

• •

•, n,

y/W)

where

., x

-,k

and

are

notations

and

as in

(II)

Definition

2.2

with

= Xj:

respectively. Also, taking

subsequence again

necessary,

we may

assume that

there

are a

constant

c <

min{r*

—

f,f

—

T,}

and n-th

points

[0,1],

k =

•

•,

such that

—>

and

Xjtk

—>

£*,

as j

—» +oo,

k =

• •

•,

since

and

[0,1]

are

compact

Moreover, putting

—

\fk(&)n

and

ft+1

:= 1,

ni/k(d)

< 1 and x

^K^)^

x^+i

for

0,1,

• •

•,

Here

let us put

(xk,

\A(i?)7r),

k =

• •

•,

n, and

(-l)

+ f for x

s/k(i))n, x

i],

k =

0,1,

• •

•,

)

-l)

ccos

(

,_^ ]

for x

Jjt,

•

,n.

/«(*)

Then, since

"\/S(*)T

ny^)7r

= ^

.,,|

< 1, j > 1

resp.

= ny

K(I?J)7T

n\Jh{'d)ir

= ^

< 1, j > 1

see

that

min{r*

- f, f

—

r»}

and x

G S

{H(d),f;n) satisfying

(4.1)

(resp. (4.2)).