Беликов В.И.(ред.) Задачи лингвистических олимпиад

Подождите немного. Документ загружается.

Семантика 141

1. s

для f — sororis neptis

2. s

′

для c

, s

′

для c

′

— materterae nepos

3. s

′

для f

, s

′

для f

′

— amitae pronepos

4. f

′

для s

, f

′

для s

′

— avunculi abneptis

5. f

для b

, f

для b

′

— patrui adnepos

6. f

′

для s — fratris trineptis

Задание 1.

Определите, кем являются

1. b

для c

2. b

для c

3. c

для s

4. f

′

для b

5. c

′

для b

6. c

для b

Задание 2.

Выразите в форме от ношений между указанными

на схеме символами следующие отношения:

1. amitae nepos

2. avunculi neptis

3. patrui proneptis

4. fratris abneptis

5. sororis adneptis

6. ma terterae trineptis

Объясните ваше решение.

Задача 239.

Значение слов, обозначающих степени родства, может быть описано как

набор значений некоторых признаков. Так, в значение слова сын и слова

дочь входит признак «пол», в первом случае имеющий значение «муж-

ской пол», во в тором — «женский пол».

Задание 1.

С помощью какого минимального числа признаков

можно описать значение следующих русских слов:

отец, мать, дед, бабка, дядя, тётка, с ын, дочь, внук, внучка, пле-

мянник, племянница —

так, чтобы каждые два слова различались хотя бы одним признаком, а

каждый признак мог принимать два значения? Какие эт о признаки?

Задание 2.

Предложите анало г ичную систему признаков для эвен-

кийского языка, где у казанным двенадцати русским словам соответ-

ствуют следующие восемь:

ам ¯ин — отец;

эн¯ин —мать;

142 Условия задач

ам¯ака — 1) дед; 2) дядя (старший брат отца, матери);

эн¯экэ — 1) бабка; 2) тётка (старшая сестра отца, матери);

ак¯ин — 1) дядя (младший брат отца, матери); старший брат;

эк¯ин —1) тётка (младшая сестра отца, матери); старшая сестра;

нэк¯ун — 1) младший брат; 2) младшая сестра; 3) внук; 4) внучка;

5) племянник; 6) племянница;

хутэ — 1 ) сын; 2) дочь.

Задача 240.

Даны слова вьетнамского и тайско го языков, обоз начающие степени

родства:

Вьетнамский:

anh — ста рш ий брат

chi

— старша я сестра

em — младший брат, младшая сестра

ch´u — дядя (младший брат отца)

b´ac — дядя (старший брат отца или матери),

тётка (старш а я сестра отца или мате ри )

cˆo — тётка (младшая с естра отца)

cˆau — дядя (младший брат матери)

d¯ı — тётка (младшая сестра матери)

Тайский:

pi’ — старший брат, старшая сестра

ng — младший брат, младшая сестра

ao — дядя (м ладший брат отца)

lun¯g — дядя (старший брат отца)

khu’ — дядя (младший брат матери)

bac — дядя (старши й брат матери)

a — тётка (младшая сестра отца)

pa’ — тётка (старшая сестра отца или мате ри)

na’ — тётка (младшая сестра матери)

Задание 1. Выделите как можно меньшее количество признаков,

по которым различаются данные термины родства в обоих языках.

Задание 2.

Определите, в каких словах эти признаки выражены,

а в каких — нет.

Задача 241.

Некоторая г ру ппа людей связана между собой родственными отношени-

ями. Если мы обозначим этих людей маленькими латинскими буквами,

Семантика 143

а родственные отношения между ними большими латинскими буквами,

то получим следующую таблицу:

a b c d e f g

a — A A B D E E

b A — A E D E E

c F F — G H I I

d H J J — K L L

e B B B N — N N

f O O D P Q — A

g J J H L K F —

Таблицу следует читать так: если на пересечении строки x и

столбца y ст оит символ Z, то это значит, что x является Z по отно-

шению к y.

Известно , что e — мужчина.

Задание.

Определите, что значит каждая большая латинская буква

в данной таблице (значение каждой из них должно выражаться по-рус-

ски одним словом).

Задача 242.

Сравните б лизкие по значению предложения (1), (2) и (3):

(1) Думаю, что Ивана простил и.

(2) Боюсь, что Ивана п ростили.

(3) Надеюсь, что Ивана п ростили.

Все они выражают некоторую долю уверенности говорящего в собы-

тии «Ивана простили», но , кроме того, в (2) и (3) выражено отно -

шение говорящего к этому событию: отрицательное в (2) и положи-

тельное в (3). Смысловые различия между (1), (2) и (3) очевидным

образом связаны со словами думать, бояться и надеяться. В отли-

чие от думать, слова бояться и надеяться заключают в своём значе-

нии оценку (оценочную пресуппозицию) говорящего: Я боюсь, что P —

‘я считаю, что Р плохо’; Я надеюсь, что P —‘я считаю, что Р хорошо’.

Слов, находящихся в таких же смысловых отношениях, как

думать —бояться —надеяться, в русском языке не так уж мало. Ниже

приводится таблица, устроенная следующим образом: сло ва (или сло-

восочетания), стоящие в одной строке в первых трёх столбцах, должны

различаться по значению только оценочными пресуппозициями (ней-

тральное отношение / отрицательная оценка / положительная оценка)

события, выраженного подчинённой им ф разой (предложением или сло-

восочетанием). Пример такой фразы содержится в четвёртом столбце

таблицы.

144 Условия задач

Отношение к событию P Пример ф разы,

не выражено отрицательное положительное выражающей событие P

довелось видеть эт о

подвигнуть на такой поступок

дойти до такого положения

в обществе

к сча стью он не понимал по-русс ки

произошло нечто не ожиданное

пожертвовал привычкой читать

лёжа

Задание. Заполните пустые (незатемнённые) клетки таблицы.

У некоторых клеток может быть несколько вариантов заполнения.

В таком случае старайтесь привести как можно больше вариантов.

(Обратите внимание: примеры в четвёртом столбце таблицы приво-

дятся в такой форме, чтобы о ни сочетались со словами, данными в

первых трёх столбцах. Слова (или словосочетания), предлагаемые ва ми

для заполнения клеток в первых трёх столбцах, могут требовать и

несколько другой формы отдельных слов в описании соб ы тия P, напри-

мер, другого падежа существительного привычка в последней строке.)

Задача 243.

В языке N на месте русских слов да и нет имеется также два слова,

но употребляются они немног о иначе. Выписанный ниже диалог — это

перевод с языка N, выполненный неопытным переводчиком, который

не заметил этого различия и всегда передавал одно из данных слов

русским да, а другое —русским нет.

(1) — Сегодня не пятница? — Н ет.

(2) — Не четырнадцатое? —Да.

(3) — Мы находимся здесь меньше недели? — Да.

(4) — Но ведь десятого был понедельник? — Нет.

(5) — Мы приехали не восьмого? — Нет.

(6) — Мы приехали в субботу? — Нет. Мы приехали в воскресенье.

(7) — Ты не ошибаешься? — Да. Я хорошо помню, что второго был

понедельник.

Задание.

Сформулируйте пра вила, по которым употребляются

в языке N слова, соответствующие русским да и нет.

• Примечание. Предполагается, конечно, что участники диалога

не допускают ни намеренной лжи, ни ло гических ошибок.

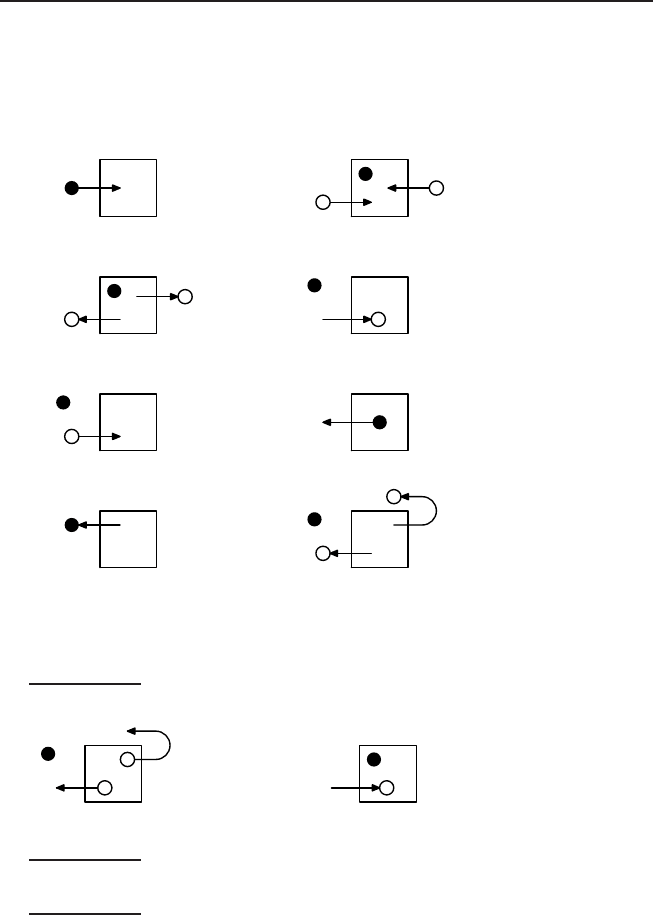
Семантика 145

Задача 244.

Ниже приводятся условные схемы некоторых ситуаций и соответству-

ющие китайские фразы (в латинской транскрипции), описывающие эти

ситуации:

Wˇo y`ao j`ınqu T¯amen y`ao j`ınlai

T¯amen ch¯uqule T¯a j`ınqule

T¯a y`ao j`ınqu Wˇo y`ao ch¯uqu

Wˇo ch¯ulaile T¯amen ch¯ulaile

Кроме т ого, известно, что по-китайски wˇomen означает ‘мы’, а nˇı —‘ты’.

Задание 1. Приведите китайские фразы, описывающие следующие

ситуации:

Задание 2. Можно ли сказать по-китайски wˇo y`ao j`ınlai ? Если да,

то как перевест и эту фразу на русский язык, если нет, то по чему?

Задание 3. Определите, какие китайские слова должны быть упо-

треблены в переводах следующих фраз:

1) «Войдите!» [в ответ на стук в дверь];

2) «Выйди вон!» [учитель — провинившемуся ученику].

146 Условия задач

Задача 245.

В школьном курсе геометрии употребляются такие выражения, как

Отрезок AB является основанием т реугольника ABC,

Треугольник ABC подобен треугольнику A

, ...

и не употребляются (по разным причинам) такие выражения, как

Треугольник ABC является основанием отрезка AB,

Треугольник ABC подобен квадрату M NP Q.

В табличке, приве дённой ниже, с помощью каждой из цифр зашиф-

ровано некоторое сказуемое (или глагольная часть сказуемого) наподо-

бие является основанием, равен (но, конечно, другие). Если в какой-то

клетке таблички проставлена цифра, то это означает, что в школьной

геометрии вполне употребима следующая фраза: подлежаще е —слово,

стоящее по горизонтали (слева), сказуемое (или его глагольная часть) —

то, что зашиф ровано этой цифрой, и дополнение (или именная часть

сказуе мого) — слово , стоящее по вертикали (дополнение можно упо-

треблять в любом падеже, с предлогом и без). Если в какой-то клетке

некоторой цифры нет, з начит, соответствующее выражение в школьной

математике не принято.

Точка A

Прямая M

Плоскость P

Точка A 4 1 1

Прямая M N 3 2, 4 1, 2

Плоскость P 3 2, 3 2, 4

Задание. Расшифруйте цифры, приведённые в табличке.

Задача 246.

Слова русского языка можно распределить по классам на основе их

сочетаемости с другими словами. Та к, например, сочетание кирпичный

дом возможно, а кирпичный дурак — нет; следовательно, слова дом и

дурак входят в разные сочетаемостные классы.

Дана группа существит е льных: земляника, чашка, остров, топор,

овраг —и список из трёх прилагательных: лесной, большой, лесистый.

Задание 1.

Разбейте группу существительных на классы так, чтобы

два слова попадали в один класс тогда и только тогда, когда они могут

сочетаться с одними и теми же прилагательными из данного списка.

Является ли какое-либ о прилагательное избыточным для получения

этой классиф икации существительных?

Задание 2. Теперь до бавьте ещё одно такое прилагательное, чт обы

при разбиении существительных каждый класс состоял ровно из одного

слова.

Семантика 147

Задание 3. Теперь расширьте группу сущ ествительных так, чтобы

при разбиении её относительно имеющихся у вас четырёх прилагатель-

ных получилось как можно больше сочетаемостных класс ов.

Кратко поясните своё решение.

Задача 247.

Даны пары конструкций:



(а) «предлог по + сущ. в дат. падеже»

(б) «предлог в + сущ. в вин. падеже»



(а) «предлог под + сущ. в вин. падеже»

(б) «предлог под + сущ. в твор. падеже»



(а) «предлог у + сущ. в род. падеже»

(б) «сущ. в дат. падеже (без предлога)»



(а) «предлог от + сущ. в род. падеже»

(б) «сущ. в твор. падеже (без предлога)»

Задание.

Придумайте русскую фразу, которая обладала бы следу-

ющим свойством: в ней е с ть конструкция 1(а), и е с ли эту конст ру к-

цию заменить на 1(б), то смысл фразы практически не изменится.

То же самое проделайте для пар конструкций 2(а) — 2(б), 3(а) — 3(б),

4(а) — 4(б).

Задача 248.

Даны предложения:

1. Слон удивляет всех большими ушами.

2. Он вёл машину пыльной дорогой.

3. Я знал её маленьким мальчиком.

4. Он читал книгу тёплым вечером.

5. Ракета пронзила облака чёрной молнией.

6. Он вскопал грядку острой лопатой.

7. Я знал его маленьким мальчиком.

8. Я считал его круглым дураком.

9. Он покинул Ленингра д вечерним поездом.

В этих предложениях творительный падеж последнего с уществи-

тельного имеет разные значения. Чтобы выяснить эту разницу, доста-

точно переделать (трансформировать) данные предложения так, чтобы

смысл их сохранился, но чтобы вместо оборота с творительным паде-

жом в них содержалась какая-либо другая гра мматическая конструк-

ция. (Разрешается трансформировать всё предложение целиком, а не

148 Условия задач

только оборот с творительным падежом.) Если какая-либо переделка

возможна для фразы А, а для фра з ы Б даёт предложение с другим

смыслом или бессмысленное предложение, т о можно заключить, что во

фразах А и Б оборот с творительным падежом имеет разное значение.

Задание.

При помощи таких трансформаций попытайтесь отличить

друг от друга как можно больше (может быть, все?) из приведённых

девяти предложений.

Задача 249.

Ниже приводятся словос очетания типа «существительное в именит е ль-

ном падеже + существительное в родительном падеже»:

1) помощь соседей 6) книга сестры

2) стирка белья 7) рукав рубахи

3) скрип колёс 8) лечение пациен т а

4) ведро воды 9) дом отца

5) радость в стречи 10) стакан молока

Можно выделить различные значения родительного падежа, учи-

тывая возможность или невозможность перестроить, с сохранением

смысла, вышеприведённые словосочетания в словосочетания следую-

щих типов.

Тип словосочетания: Пример:

сущ. в им. пад. + глагол молоток стучит

сущ. в вин. пад. + глагол 3-го лица мн. ч. п латья кроят

сущ. в им. пад. + часть + сущ. в род. пад. дверь — часть дома

сущ. в им. пад. + п ринадлежит + пруд принадле ж ит

+ сущ . в дат. пад. санат орию

сущ. в им. пад. + п ри + сущ. в предл. пад. веселье при драке

При перестройке в итоговом словосочетании на месте переменных

разрешается использовать только слова тог о же корня, что слова исход-

ного словосочетания (переменными считаются элементы , обозначенные

выше с помощь ю грамматических терминов).

Задание 1. Выделите (описанным способом) ра з личные значе-

ния родительного падежа и укажите, какие исходные сло восочетания

используют каждое из этих значений.

Задание 2.

Попытайтесь описать каждое выделенное ва ми значе-

ние родительного падежа.

Семантика 149

Задача 250.

Ниже приводятся словос очетания типа «существительное в именит е ль-

ном падеже + от + существительное в родительном падеже»:

1) ручка от чемодана 6) порошки от боли

2) смерть от раны 7) свет от лампы

3) дорога от леса 8) ключ от дома

4) запах от нафталина 9) крик от боли

5) потери от засухи 10) великан от рождения

Можно выделить различные значения предло га от, учитывая во з -

можность или невозможность перестроить, с сохранением смысла,

вышеприведённые словосочетания в слово с очетания следующих типов:

Тип словосочетания: Пример:

сущ. в им. пад. + причина + сущ. в род. пад. война — п ричина горя

сущ. в им. пад. + п ротив + сущ. в род. пад. лекарство против цин ги

сущ. в им. пад. + источник + сущ. в род. пад. печка —источник тепла

сущ. в им.пад.+принадлежит + сущ . в дат.пад. дверь принадлежит дому

сущ. в им. пад. + с + сущ. в род. пад. время с полуночи

При перестройке в ито г овом словосочетании на месте перемен-

ных разрешается использовать толь ко слова исходного словос очетания

(переменными в итоговом словосочетании считаются невыделенные эле-

менты).

Задание 1.

Выделите описанным способом различные значения

предлога от и укажите, какие исходные словосочетания использу ют

каждое из этих значений.

Задание 2.

Попытайтесь описать каждое выделенное ва ми значе-

ние предлога от.

Задача 251.

Даны слово сочетания на шу гнанском языке с их переводами на русский

язык:

кузаа хац — кувшин воды

чалак зима адь —ведро земли

тамбал бююн — борода бездельника

бииг дююнаа — горшок зе рна

кузаа гъэв — крышка кувшина

беечораа зимаадь — земля бедняка

Задание.

Переведите на ш угнанский язык:

ведро воды, зерно бедняка, кувшин бездельника.

150 Условия задач

Задача 252.

В каждом языке имеются мног означные слова , т. е. слова, имеющие

несколько значений. Отдельные значения таких слов связаны опреде-

лёнными отношениями: иголка (швейная) —иголка (хв ойного дерева) —

сходство по фо рме; шляпка (женская) — шл япка (гвоздя) —сходство в

расположении предмета отно с ительно чего- либо; аудитория (по меще-

ние) — аудитория (слушатели) — пространст венная смежность и т. п.

Задание 1.

Приведите ещё по 2–3 примера на данные в условии

отношения.

Задание 2.

Какие ещё отношения могут связывать о тдельные зна-

чения многозначных слов? Приведите примеры (4 отношения, по 2–3

примера на каждое).

Задание 3. Какие ещё значения могут быть у многозначного слова,

если одно из его значений —‘голова (часть тела)’? Учтите, что русское

слово голова не обязательно имеет все те значения, которые, вообще

говоря, возможны у такого многозначного слова.

Задача 253.

Предложение Кружок спелся имеет, теоретически говоря, четыре зна-

чения, так как слово кружок имеет два значения:

1) уменьшительное к слову круг в смысле определённого неодушёвлен-

ного физического объекта;

2) группа людей, объединённых какими-либо связями, —

и слово спеться имеет два значения:

1) научиться хорошо петь вместе;

2) достигнуть со гласова нности в поступках.

Но реально в русском языке это предложение выражает не четыре,

а лишь два значения, пот ому что и первое и вто рое значения глагола

как бы связаны в своём употреблении ограничительными признаками

«относиться к лицу» или «относиться к группе лиц». А первое значе-

ние существительного кружок не удо влетворяет этим ограничитель ным

признакам и не может, следовательно, сочетаться с данным глаголом

ни в первом, ни во втором значении. Ограничительными признаками

бывают связаны в своём употреблении не только глаголы, но и прила-

гательные.

Задание.

Определите, сколько теоретически мыслимых и реально

возможных в русском языке значений имеет предложение Блестящи й

язык был отмечен начальником.

Дайте обоснование своему решению.