Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика

Подождите немного. Документ загружается.

Гл.

Экономика

страхования

1.5.1,

показав

сначала,

что

(х

- z)(2z),

затем

проверив,

что

[х

I(х))2

[х

Id*

(х))2

[Id*

(х)

I(х)][2х

2Id*

(х))

2[Id*

(х)

- I(x))d*.

Искомое

неравенство

можно

проверить,

разбивая

доказательство

на

три

случая.

Чтобы

дать

еще

одно

доказательство,

заметим,

что

при

соответствующем

выборе

размера

капи

тала

функции

полезности

результат

настоящего

упражнения

является

частным

случаем

теоремы

1.5.1.]

1.22.

Пусть

выполнены

предположения

теоремы

1.5.1,

за

исключением

бюджетного

ограничения.

То

есть

принимающее

решения

лицо

готово

выплатить

премию

Р,

Е[Х]

,"",

которая

максимизирует

ожидаемую

полезность.

Кроме

того,

предположим,

что

любое

допустимое

страхование

может

быть

приобретено

за

сумму,

равную

его

ожидаемой

стоимости.

Докажите,

что

оптимальным

страхованием

будет

Iо(х).

Этот

результат

может

быть

сформулирован

так:

полное

страховое

покрытие

оптимально

случае

отсутствия

бюд

жетных

ограничений,

если

страхование

может

быть

приобретено по

цене

его

нетто-премии.

[Указание.

Воспользуйтесь

леммой,

которой

роль

играет

w -

I(х)

Р,

роль

играет

w -

+Io(x)

Е(Х)

=w -

Jl.

Возьмите

математические

ожидания

проверьте,

что

E[u(w -

Х)

I(Х)

Р)

u(w -

Jl).)

1.23.

теореме

1.5.1

упр.

1.21

были

установлены

свойства

оптимальности

стра

хования

эксцедента

убыточности.

Эти

свойства

зависят

от

критерия,

согласно

которому

принимается

решение,

от

ограничений,

также

от

наличия

других

страховых

возможно

стей.

каждом

из

указанных

рассуждений

имелись

бюджетные

ограничения.

Рассмотрим

ситуацию,

когда

имеются

ограничения

на

риск

когда

цена

страхования

зависит

от

стра

хового

риска,

измеренного

помощью

дисперсии.

(i)

Страховая

премия

равна

E[I(X))

j(D[I(X))),

где

j(w)

является

возрастающей

функцией.

Величину

j(D[I(X)))

можно

интерпретировать

как

рuс~овую

'Н,адбав~у.

(ii)

Лицо,

принимающее

решения,

решает

удержать

потери

-I(X),

такие,

что

D[X-

I(X))

= V

О.

Это

требование

налагает

не

бюджетные,

рисковые

ограничения.

Констан

та

определяется

степенью

несклонности

риску,

свойственной

принимающему

решения.

Критерий

принятия

решений

теории

портфельного

инвестирования

состоит

том,

чтобы

фиксировать

допустимую

дисперсию,

затем

оптимизировать

ожидаемые

результаты.

(iii)

Лицо,

принимающее

решения,

выбирает

функцию

I(х),

которая

минимизирует

j(D[I(X)]).

Целью

является

минимизация

рисковой

надбавки,

которая

равна

выплаченной

премии

минус

ожидаемые

страховые

выплаты.

Выполним

следующие

шаги:

(а)

E[I(X)]

=V +

Е(Х)

- 2

Соу[Х,

I(Х)].

(Ь)

Величина

I(х),

которая

минимизирует

D[I(X)),

следовательно,

j(D[I(X))),

такова,

что

коэффициент

корреляции

между

I(Х)

равен

(с)

Известно,

что

если

две

случайные

величины

имеют

коэффициент

корреля

ции,

равный

то

P{W

Ь,

где

О}

= 1.

Иначе

говоря,

вероятность

того,

что

их

совместное

распределение

сосредоточено

на

прямой,

имеющей

положительный

наклон,

равна

п.

(Ь)

было

показано,

что

коэффициент

корреляции

между

I(Х)

ра

вен

Таким

образом,

I(Х)

аХ

Ь,

откуда

следует,

что

I(Х)

а)Х

Ь.

ДЛЯ

допустимого

страхования

I(х)

или

(l-а)х-Ь

х.

Из

этих

неравенств

следует,

что

1 -

(d)

Для

определения

будем

считать,

что

коэффициент

корреляции

между

I(Х)

равен

или,

что

то

же

самое,

их

ковариация равна

произведению

их

стан-

дартных

отклонений.

По

кажите

что

этом

случае

.jV/D[X]

страхование,

которое

минимизирует

j(D[X))

соответствует

I(Х)

JV/D[X]]X.

МОДЕЛИ

ИНДИВИДУАЛЬНЫХ

РИСКОВ

НА

КОРОТКОМ

ИНТЕРВАЛЕ

ВРЕМЕНИ

2.1.

Введение

гл.

мы

рассматривали

вопрос,

как

лицо,

принимающее

решения,

может

использовать

страхование

для

уменьшения

неблагоприятного

финансового

воздей

ствия

некоторых

типов

случайных

событий.

Это

рассмотрение

было

весьма

общим.

Под

лицом,

принимающим

решения,

мог

подразумеваться

как

отдельный

человек,

ищущий

защиту

от

ущерба,

причиняемого

собственности,

сбережениям

или

доходам,

так

организация,

ищущая

защиту

от

того

же

рода

ущерба.

На

самом

деле

такой

ор

ганизацией

может

оказаться

страховая

компания,

которая

ищет

способы

защитить

себя

от

финансовых

потерь

из-за

слишком

большого

числа

страховых

случаев,

про

изошедших

отдельным

ее

клиентом

или

ее

страховым

портфелем.

Такая

защита

называется

nересmрахова'Ние,м

будет

введена

следующей

главе.

Теория,

изложенная

гл.

требует

введения

вероятностной

модели

для

потен

циальных

потерь.

Сейчас

мы

рассмотрим

одну

из

двух

моделей,

широко

используе

мых

определении

страховых

тарифов

резервов,

также

перестраховании

Обозначим

через

величину

случайных

потерь страховой

компании

по

некото

рой

части

ее

рисков.

этом

случае

является

случайной

величиной,

для

которой

мы

должны

определить

распределение

вероятностей.

Исторически

для

распределений

С.в.

имелось

два

набора

постулатов.

Модель

индивидуальных

рисков

определяет

следующим

образом:

(2.1.1)

где

С.в.

обозначает

потери,

причиненные

объектом

страхования

номером

обозначает

общее

количество

объектов

страхования.

Обычно

предполагается,

что

являются

независимыми

случайными

величинами,

поскольку

этом

случае

проще

математические

расчеты

не

требуется

сведений

характере

зависимости

между

ними.

Второй

моделью

является

модель

коллективных

рисков,

описанная

гл.

12.

Модель

индивидуальных

рисков,

рассматриваемая

этой

главе,

не

отражает

изменения

ценности

денег

течением

времени.

Это

делается

для

упрощения

модели,

именно

поэтому

заглавии

говорится

коротком

интервале

времени.

гл.

4-11

рассматриваются

модели

на

протяженных

интервалах

времени.

этой

главе

мы

будем

рассматривать

только

за,мх:нуmъtе

модели,

т.

е.

те,

ко

торых

число

объектов

страхования

формуле

(2.1.1)

известно

зафиксировано

самом

начале

рассматриваемого

интервала

времени.

Если

мы

вводим

предполо

жения

наличии

миграции

из

или

страховую

систему,

то

получаем

оmх:рЬtmую

модель.

Гл.

Модели

индивидуальных

рисков

2.2.

Случайные

величины,

описывающие

индивидуальные

выплаты

Сначала

напомним

основные

положения,

касающиеся

страхования

жизни.

При

страховании

на

слу'Чаu

смерти

'На

срох:

оди'Н

год

страховщик

обязуется

выплатить

величину

Ь,

если

страхователь

умрет

течение

года

момента

заключения

дого

вора

страхования,

не

выплачивает

ничего,

если

страхователь

проживет

этот

год.

Вероятностьнаступления

страхового

случая

течение

указанного

года

обозначается

через

Случайная

величина

Х,

описывающая

страховые

выплаты,

имеет

распре

деление,

которое

может

задаваться

либо

функцией

вероятностей

{

fx(x)

Р(Х

=х)

О,

Ь,

остальных

случаях,

(2.2.1)

либо

соответствующей

функцией

распределения

{

О,

Fx(x)

Р(Х

~x)

О,

Ь,

Ь.

(2.2.2)

Из

формулы

(2.2.1)

из

определения

моментов

получаем

Е[Х]

bq,

Е[х

]

= b

D[X] = b

q(1 - q).

Эти

формулы

можно

также

получить,

записав

виде

=Ib,

(2.2.3)

(2.2.4)

(2.2.5)

где

постоянная

величина,

выплачиваемая

на

случай

смерти,

1 -

случайная

ве

личина,

принимающая

значение

при

наступлении

смерти

О в

противном

случае.

Таким

образом,

Р(I

О)

=1 - q

Р(I

=q,

среднее

значение

дисперсия

С.в.

равны

q(l

соответственно, а

среднее

значение

дисперсия

С.в.

равны

q(1

- q),

что

совпадает

выписанными

выше

формулами.

Случайная

величина

областью

значений

{О,

широко

применяется

акту

арных

моделях.

учебниках

по

теории

вероятностей

она

называется

и'Ндих:атором,

бернуллuевсх:оu

слу'Чаuной

велu'Чuноu

или

бuно,м,uальной

слу'Чаuной

велu'Чu'Ной

схе

ме

единственного

испытания.

Мы

будем

называть

ее

индикатором

из

соображений

краткости,

также

потому,

что

она

указывает

наступление,

1 =1,

или

ненаступле

ние,

1 =

О,

рассматриваемого

события.

Перейдем

поиску

более

общих

моделей,

которых

величина

страховой

выпла

ты

также

является

случайной

величиной

рассматриваемом

интервале

времени

может

про

изойти

несколько

страховых

случ~в.

Страхование

на

случай

болезни,

страхование

автомобилей

прочих

видов

собственности,

также

страхование

гра

жданской

ответственности

сразу

же

предоставляют

множество

примеров.

Обобщая

формулу

(2.2.5),

положим

= 1

В,

(2.2.6)

где

случайная

величина,

описывающая

страховые

выплаты

рассматриваемом

интервале

времени,

С.В.

обозначает

общую

величину

выплат

этом

интервале

С.в.

является

индикатором

для

события,

состоящего

том,

что

произошел

по

2.2.

Случайные

величины,

описывающие

индивидуальные

выплаты

меньшей

мере

один

страховой

случай.

Являясь

индикатором

такого

события,

С.в.

фиксирует

наличие

= 1)

или

отсутствие

(1 =

О)

страховых

случаев

этом

интервале

времени,

но

не

количество

страховых

случаев

нем.

Вероятность

Р(I

по-прежнему

будет

обозначаться

через

Обсудим

несколько

примеров

определим

распределение

случайных

величин

некоторой

модели.

Рассмотрим

сначала

страхование

на

случай

смерти

на

срок

один

год

дополнительной

выплатой,

если

смерть

наступила

результате

несчастно

го

случая.

Для

определенности

предположим,

что

если

смерть

произошла

резуль

тате

несчастного

случая,

то

величина

выплаты

составит

50000.

При

наступлении

смерти

по

прочим

причинам

величина

выплаты

составит

25000.

Предположим,

что

для

лица

данного

возраста,

состояния

здоровья

профессии

вероятность

смерти

результате

несчастного

случая

течение

года

равна

0,0005,

вероятность

смерти

по

прочим

причинам

равна

0,0020.

виде

формулы

это

выглядит

так:

Р(1

000) =0,0005

Р(1

000)

::::

0,0020.

Суммируя

по

всем

возможным

значениям

В,

получим

Р(1

=0,0025,

так

что

Р(1

О)

= 1 -

Р(1

= 0,9975.

Условное

распределение

С.в.

при

условии

1 = 1

имеез:

вид

Р(В=

0001

Р(В=

000, 1=

= 0,0020 =

Р(1

0,0025'

Р(В=

000011=1)

P(B=50000,I=1)

= 0,0005

=02.

Р(I

0,0025'

Рассмотрим

теперь

страхование

автомобилей

от

столкновений

(возмещение

выпла

чивается

собственнику

автомобиля

за

ущерб,

нанесенный

его

автомобилю)

вели

чиной

безусловной

франшизы

250

максимальным

размером

выплаты

2000.

Для

наглядности

предположим,

что

вероятность

наступления

одного

страхового

случая

рассматриваемый

период

времени

для

отдельного

лица

составляет

0,15,

вероят

ность

наступления

более

чем

одного

столкновения

равна

нулю:

Р(I

О)

= 0,85,

P(I

= 0,15.

Нереалистическое

предположение

том,

что

течение

одного

периода

может

про

изойти

не

более

одного

страхового

случая,

делается

для

того,

чтобы

упростить

рас

пределение

с.в.

В.

Мы

откажемся

от

этого

предположения

следующем

разделе

после

того,

как

рассмотрим

распределение

суммы

нескольких

страховых

случаев.

Поскольку

является

величиной

выплат

страховщика,

а не

ущербом,

нанесенным

автомобилю,

мы

можем

рассматривать

две

характеристики,

В.

Во-первых,

собы

тие

1 =

включает

себя

те

столкновения,

которых

ущерб

меньше,

чем

безуслов

ная

франшиза,

которая

равна

250.

Во-вторых,

распределение

С.в.

будет

иметь

«сгусток>}

вероятностной

массы

точке

максимального

размера

страховых

выплат,

который

равен

2000.

Предположим,

что

вероятностная

масса,

сосредоточенная

этой

точке,

равна

0,1.

Далее,

предположим,

что

величину страховых

выплат

ин

тервале

от

до

2000

можно

моделировать

непрерывным

распределением

функцией

плотности,

пропорциональной

1 -

х/2000

для

< 2000.

(На

практике

непре

рывная

кривая,

которая

выбирается

для

представления

распределения

страховых

Гл.

Модели

ИНдИвидуальных

рисков

выплат,

является

результатом

исследований

размеров

выплат

предыдущем

пери

оде.)

Суммируя

эти

предположения

об

условном

распределении

с.в.

при

условии

1 = 1,

мы

приходим

распределению

смешанного

типа,

имеющему

положительную

плотность

интервале

от

до

2000

некоторый

«сгусток»

вероятностной

массы

точке

2000.

Это

иллюстрируется

графиком

на

рис.

2.2.1.

Функция

распределения

этого

условного

распределения

выглядит

так:

{

О,

Р(В

= 0,9[1 -

х/2000)2],

О,

< 2000,

2000.

~(x)

1,0

0,9

2000

(2.2.7)

Рис.

2.2.1.

Функция

распределения

С.В.

при

условии

1 = 1

разд.

2.4

мы

увидим,

что часто

используются

моменты

случайной

величи

ны

описывающей

страховые

выплаты,

частности,

ее

математическое

ожидание

дисперсия.

Вычислим

математическое

ожидание

дисперсию

рассматриваемом

примере

автомобильным

страхованием

двумя

способами.

Во-первых,

выпишем

рас

пределение

С.в.

воспользуемся

им

для

расчета

Е[Х]

D[X].

Обозначая

через

(х)

функцию

распределения

С.В.

Х,

имеем

Рх(х)

Р(Х

х)

P(IB

х)

Р(I

11=

О)

Р(I

О)

Р(I

I1=

Р(I

=1).

Для

(х)

= 0(0,85) +0(0,15) =

О.

Для

< 2000

Рх(х)

=1(0,85) +

0,9

2;00)

(0,15).

Для

2000

рх

(х)

= 1(0,85) +1(0,15) =

Это

распределение

смешанного

типа.

Как

показано

на

рис.

2.2.2,

оно

имеет

как

дис

кретную

(<сгусток»

вероятностной

массы

точке

2000),

так

непрерывную

часть.

Такой

функции

распределения

соответствует

комбинация

функции

вероятно

стей

Р(Х

О)

= 0,85,

Р(Х

=2000) =0,015,

(2.2.8)

2.2.

Случайные

величины,

описывающие

индивидуальные

выплаты

~(x)

1,000

0,985

0,850

2000

Рис.

2.2.2.

Функция

распределения

с.в.

функции

плотности

fx(x)

{oF~(X)

0,000135(1-

х/2000),

< 2000,

для

остальных

х.

Моменты

С.в.

можно

подсчитать

следующим

образом:

(2000

E(X

]

Р(Х

О)

+(2000)k .

Р(Х

= 2000) + J

fx(x)

dx.

частности,

Е(Х]

= 120

Е(х

]

= 150000.

Поэтому

(2.2.9)

D[X]

= 135600.

Имеется

ряд

формул,

связывающих

моменты

случайных

величин

условными

ма

тематическими

ожиданиями.

Для

математического

ожидания

для

дисперсии

эти

формулы

имеют

вид

E[W] = E(E(W IV]],

D[W]

= D(E[WI

V]]

+E[D(WIV]].

(2.2.10)

(2.2.11)

Подразумевается,

что

выражения

левых

частях

этих

равенств

вычисляются

непо

средственно

по

распределению

С.в.

При

вычислении

выражений

правых

частях,

именно

E[W I

D[W

IV],

используется

условное

распределение

С.в.

при

фик

сированном

значении

с.в.

Эти

выражения

являются,

таким

образом,

функциями

с.в.

мы

можем

вычислить

их

моменты,

используя

распределение

с.в.

Условные

распределения

используются

во

многих

актуарных

моделях,

это

поз

воляет

непосредственно

применять

выписанные

выше

формулы.

нашей

модели

[В.

Рассматривая

С.в.

качестве

с.в.

[

качестве

получаем

Запишем

Е(Х]

Е(Е(Х

[]],

D[X]

=D[E(XI

1]]

E[D[X

[]].

J.L

E[BII=l],

0'2

=D(BII=l]

(2.2.12)

(2.2.13)

(2.2.14)

(2.2.15)

Гл.

Модели

индивидуальных

рисков

рассмотрим

условные

математические

ожидания

E[XII=O]

О,

Е[Х

I1=

Е[В

I1=

р.

(2.2.16)

(2.2.17)

Формулы

(2.2.16)

(2.2.17)

определяют

Е[Х

как

функцию

ОТ

с.в.

что

может

быть

записано

виде

следующей

формулы:

Е[Х

J.lI.

Значит,

Е[Е[Х

1]]

= J.lE[I] =

J.lq,

D[E[X

11]]

J.L

D[I]

J.l2

q).

Так

как

при

1 =

О,

то

D[XII=O]

О.

Для

1 = 1

мы

имеем

= в

[Х

I1=

[В

I1=

0'2.

Формулы

(2.2.21)

(2.2.22)

можно

объединить:

D[X

11]

0'21.

Таким

образом,

E[D[X

11]]

E[I] =

Подставляя

(2.2.21), (2.2.20)

(2.2.24)

(2.2.12)

(2.2.13),

мы

получаем

Е[Х]

J.lq,

D[X]

J.l2

(2.2.18)

(2.2.19)

(2.2.20)

(2.2.21)

(2.2.22)

(2.2.23)

(2.2.24)

(2.2.25)

(2.2.26)

Применим

полученные

формулы

для

вычисления

Е[Х]

D(X)

при

мере

автомо

бильного

страхования

(рис.

2.2.2).

Поскольку

функция

плотности

С.в.

при

условии

1 = 1

выражается

формулой

lв

/(х

11)

= {0,0009(1 -

х/2000),

< 2000,

для

остальных

х,

причем

Р(В=

2000! 1=

= 0,1,

мы

имеем

J.I

=12000

0,0009Х(1-

2;00)dX

+(0,1)(2000) =800,

Е[В

= 12000

0,0009х

2;00)

dx +(0,1)(2000)2 = 1000000,

0'2

1000000

- (800)2 =360000.

Наконец,

полагая

q = 0,15,

из

формул

(2.2.25)

(2.2.26)

мы

получим

следующие

равенства:

Е[Х)

=800(0,15) = 120,

D[X) =(800)2(0,15)(0,85) +(360000)(0,15) =135600.

2.3.

Суммы

независимых

случайных

величин

Для

описания

другой

страховой

ситуации

можно

предложить

другие

модели

для

С.в.

В.

качестве

примера

рассмотрим

модель

для

числа

смертей,

произошедших

результате

авиационных

катастроф

за

годичный

период

деятельности

авиакомпа

нии.

Мы

можем

начать

со

случайной

величины

Х,

описывающей

число

смертей

для

одного

рейса,

потом

просуммировать

такие

случайные

величины

по

всем

рейсам

за

год.

Для

одного

рейса

событие

1 = 1

будет обозначать

наступление

авиакатастрофы.

Число

смертей,

которое

повлекла

за

собой

эта

катастрофа,

будет

представляться

произведением

двух

случайных

величин

где

L -

коэффициент

загруженно

сти

самолета,

т.

е.

число

лиц,

находившихся

на

борту

момент

авиакатастрофы,

доля

смертельных

исходов

среди

лиц,

находившихся

на

борту.

Число

смертей

представляется

именно

таким

образом,

поскольку

раздельная

статистика

для

вели

чин

бывает

более

доступной,

чем

статистика

для

с.в.

В.

Итак,

ILQ.

Хотя

доля

смертельных

исходов

среди

лиц,

находившихея

на

борту,

число

лиц,

находив

шихся

на

борту,

вероятно,

связаны

между

собой,

качестве

первого

приближения

можно

предположить,

что

С.в.

независимы.

2.3.

Суммы

независимых

случайных

величин

модели

индивидуальных

рисков

страховые

выплаты,

производимые

страховой

компанией,

представляются

как

сумма

выплат многим

отдельным

лицам.

большинстве

приложений

страховые

выплаты

отдельным

лицам

предполага

ются

независимыми.

этом

разделе

мы

напомним

два

метода

определения

распре

деления

суммы

независимых

случайных

величин.

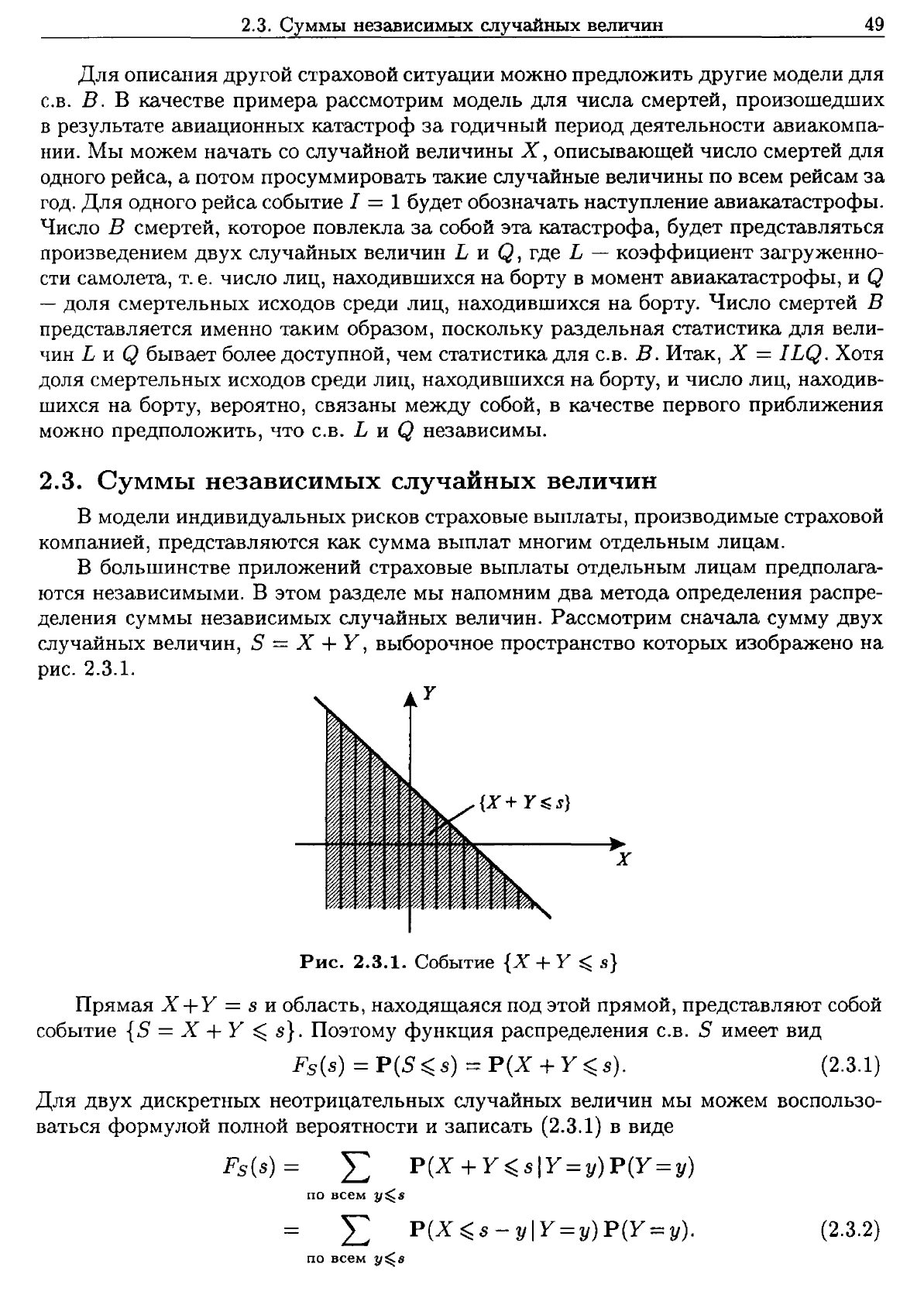
Рассмотрим

сначала

сумму

двух

случайных

величин,

S =

У,

выборочное

пространство

которых

изображено

на

рис.

2.3.1.

(2.3.2)

Рис.

2.3.1.

Событие

{Х

Прямая

+У

= s

область,

находящаяся

под

этой

прямой,

представляют

собой

событие

{В

s}.

Поэтому

функция

распределения

С.в.

имеет

вид

Fs(s) =

Р(В

s) =

Р(Х

s). (2.3.1)

Для

двух

дискретных

неотрицательных

случайных

величин

мы

можем

воспользо

ваться

формулой

полной

вероятности

записать

(2.3.1)

виде

Fs(s) = L

P(X+Y~sIY=Y)P(Y=y)

по

всем

y::;;s

Р(Х~s-уIУ=у)Р(У=у).

по

всем

у::;;а

Гл.

Модели

индивидуальных

рисков

Если

независимы,

последняя

сумма

может

быть

переписана

виде

FS(8) =

по всем

y~a

РХ

y)fy(y).

(2.3.3)

Функция

вероятностей,

соответствующая

этой

функции

распределения,

может

быть

найдена

по

формуле

fS(8) =

fX(8 -

y)fy(y).

(2.3.4)

по

всем

Y~B

ДЛЯ

непрерывных

неотрицательных

случайных

величин

формулы,

соответствую

щие

формулам

(2.3.2), (2.3.3)

(2.3.4),

имеют

вид

Fs(s) =

1'Р(Х~S-УIУ=У)fу(У)dУ,

(2.3.5)

Рф)

= [

рх(в

y)fy(y)

dy, (2.3.6)

fs(s)

= [

fx(s

y)fy(y)

dy. (2.3.7)

Когда

либо

одна,

либо

обе

случайные

величины

имеют

распределение

сме

шанного

типа

(что

характерно

для

моделей

индивидуальных

рисков)

формулы

ана

логичны,

но

более

громоздки.

Для

случайных

величин,

которые

могут

принимать

также

отрицательные

значения,

суммы

интегралы

приведенных

формулах

бе

рутся

по

всем

значениям

у от

-QO

до

+00.

теории

вероятностей

операция

формулах

(2.3.3)

(2.3.6)

называется

сверm

'К;оu

двух

функций

распределения

Fx(x)

Fy(y)

обозначается

через

Fy.

Операция

свертки

может

также

быть

определена

для

пары

функций

вероятностей

или

функций

плотности

помощью

формул

(2.3.4)

(2.3.7).

Для

определения

распределения

суммы

более

чем

двух

случайных

величин

мы

можем

использовать

итерации

процесса

взятия

свертки.

Для

S = X

...

где

являются

независимыми

случайными

величинами,

обозначает

функцию

распределения

С.в.

F(k)

является

функцией

распределения

с.в.

+ ...

мы

получим

F(2)

р(1)

F(З)

F(2)

F(4)

F(З>'

F(n)

= F

F(n-l).

Пример

2.3.1

иллюстрирует

эту

процедуру

для

трех

дискретных

случайных

ве

личин.

Пример

2.3.1.

Случайные

величины

Х2

независимы

имеют

распре

деления,

которые

определяются

столбцами

(1), (2)

(3)

приведенной

ниже

таблицы.

Выпишем

функцию

вероятностей

функцию

распределения

с.в.

S =X

Решение.

таблице

используются

обозначения,

введенные

перед

примером:

•

столбцах

(1)-(3)

содержится

имеющаяся

информация.

2.3.

Суммы

независимых

случайных

величин

•

Столбец

(4)

получен

из

столбцов

(1)

(2)

применением

(2.3.4).

•

Столбец

(5)

получен

из

столбцов

(3)

(4)

применением

(2.3.4).

Определение

столбца

(5)

завершает

нахождение

функции

вероятностей

для

С.в.

В.

Ее

функция

распределения

столбце

(8)

является

набором

частичных

сумм

(1) (2) (3)

(4) (5) (6)

(7)

(8)

Л(х)

f2(X)

fз(х)

/(2)

(х)

f(З)(х)

Рl(Х)

р(2)

(х)

р(З)

(х)

0,4 0,5

0,6 0,20 0,120

0,4 0,20

0,120

0,3

0,2 0,0 0,23 0,138

0,7 0,43

0,258

0,2 0,1

0,1

0,20 0,140

0,9

0,63 0,398

0,1 0,1

0,1

0,16 0,139 1,0 0,79 0,537

0,0

0,1

0,11 0,129

1,0

0,90 0,666

0,0 0,0

0,1

0,06

0,115

1,0

0,96

0,781

0,0 0,0

0,0 0,03 0,088 1,0 0,99 0,869

7 0,0 0,0 0,0

0,01

0,059 1,0 1,00 0,928

8 0,0 0,0 0,0

0,00

0,036 1,0 1,00 0,964

9 0,0 0,0 0,0

0,00

0,021

1,0 1,00 0,985

0,0 0,0 0,0

0,00

0,010

1,0 1,00 0,995

0,0 0,0 0,0

0,00

0,004

1,0

1,00 0,999

0,0

0,00 0,001 1,0 1,00

1,000

столбца

(5),

начиная

сверху.

Для

наглядности

мы

включили

столбец

(6),

функцию

распределения

для

столбца

(1),

столбец

(7),

который

можно

получить

непосредствен-

но

из

столбцов

(1)

(6),

при

меняя

(2.3.3),

столбец

(8),

определяемый

аналогично

по

столбцам

(3)

(7).

Столбец

(5)

можно

определить

из

столбца

(8)

последовательным

вычитанием.

...

Перейдем

рассмотрению

двух

примеров

непрерывными

случайными

величи-

нами.

При

мер

2.3.2.

Пусть

С.в.

имеет

равномерное

распределение

на

интервале

(0,2),

пусть

С.в.

не

зависит

от

С.в.

И имеет

равномерное

распределение на

интервале

(0,3).

Определим

функцию

распределения

С.в.

S =

У.

Решение.

Поскольку

распределения

с.в.

непрерывны,

воспользуемся

формулой

(2.3.6):

Тогда

{

О,

Fx(x)

х/2,

О,

fy(y)

= {

~/3,

< 3,

для

остальных

у.

Fs(s) = [

Fx(s

y)fy(y)

dy.

Выборочное

пространство

С.в.

иллюстрируется

рис.

2.3.2.

Прямоугольная

область

содержит

все

возможные

значения

пары

и У.

Интересующее

нас

событие,

+ у

изображается

на

рисунке

для

пяти

значений

Для

каждого

значения

прямая

пересекает

ось

точке

прямую

= 2

точке

s - 2.

Значения

функции