Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


22
Гл.
1.
Экономика
страхования
•
Неожиданно
начавшаяся
продолжительная
болезнь
может
привести
к
фи
нансовым
потерям.
Эти
потери
состоят
как
из
дополнительных
расходов
на
лечение,
так
и
из
сокращения
заработка.
•
Смерть
молодого
совершеннолетнего
человека
может
наступить
тогда,
когда
его
долгосрочные
деловые
и
семейные
обязательства
еще
не
выполнены.
Или
же
средства
не
которого
лица,
дожившего
до
преклонного
возраста,
могут
оказаться
недостаточными
для
обеспечения
ему
прожиточного
минимума.
Эти
примеры
призваны
проиллюстрировать
следующее
определение.
Институт
страхования
(система
страхования)
-
это
механизм
сокращения
неблагоприятного
финансового
влияния
случайных
событий,
которые
препятствуют
исполнению
разумных
ожиданий.
Полезно
различать
институт
страхования
и
близкие
к
нему
системы.
Банковские
учреждения
были
созданы
для
получения,
инвестирования
и
распределения
сбере
жений
отдельных
физических
и
юридических
лиц.
Входящие
и
исходящие
денежные
потоки
сберегательного
учреждения
не
являются
детерминированными.
Однако
в
отличие
от
систем
страхования
сберегательные
учреждения
не
производят
плате
жей,
основанных
на
величине
финансовых
потерь,
которые
происходят
вследствие
события,
на
которое
не
могут
влиять
те,
кто
страдает
от
его
последствий.
Другой
системой,
которая
производит
выплаты,
основанные
на
наступлении
слу
чайного
события,
является
азартная
игра.
Однако
азартные
игры
или
пари
отли
чаются
от
страхования
тем,
что
система
страхования
предназначена
для
защиты
от
негативного
экономического
влияния
рисков,
которые
существуют
независимо
от
застрахованного
и
контролировать
которые
он,
как
правило,
не
может.
Типич
ная
схема
азартной
игры
определяется
правилами
выплат
в
связи
с
реализацией
преднамеренно
вызываемого
события, и
игроки
добровольно
идут
на
риск.
Как
и
в
страховании,
при
азартной
игре
обычно
перераспределяются
денежные
средства,
но
на
этом
сходство
и
заканчивается.
Наше
определение
института
страхования
намеренно
широко.
Оно
включает
в
себя
системы,
которые
покрывают
как
ущерб,
связанный
с
собственностью,
так
и
ущерб,
связанный
с
человеческой
жизнью.
Мы
намереваемся
рассматривать
как
си
стемы
страхования,
основанные
на
индивидуальном
решении
участвовать
в
них,
так
и
системы,
где
участие
является
условием
получения
работы
или
права
на
житель
ство.
Эти
темы
обсуждаются
в
разд.
1.4.
Экономическое
обоснование
института
страхования
состоит
в
том,
что
он
спо
собствует
общему
благосостоянию,
увеличивая
уверенность
в
том,
что
намеченные
планы
не
будут
разрушены
случайными
событиями.
Такие
системы
также
могут
повышать
совокупное
производство,
поскольку
стимулируют
отдельных
людей
и
корпорации
браться
за
такие
предприятия,
в
которых
имеется
риск
больших
потерь
и
за
которые
они
не
взялись
бы
при
отсутствии
страховой
защиты.
При
мер
такого
типа
дает
развитие
морского
страхования,
поскольку
оно
уменьшает
финансовые
последствия
гибели
судов
на
море.
Международная
торговля
способствует
процес
су
специализации
и
повышению
эффективности
производства.
Но
взаимовыгодная
торговля
была
бы
чревата
слишком
большим
риском
для
некоторых
потенциаль
ных
торговых
партнеров,
если
бы
не
существовало
системы
страхования,
которая
покрывает
возможные
убытки
при
морских
перевозках.

1.2.
Теория
полезности
23
1.2.
Теория
полезности
Если
бы
люди
могли
предсказать
заранее
последствия
своих
решений,
их
жизнь
была
бы
более
простой,
но
менее
интересной.
Мы
все
принимаем
решения,
основы
ваясь
на
предпочтениях,
которые
отдаем
некоторым
последствиям.
Однако
мы
не
обладаем
даром
абсолютного
предвидения.
При
самом
лучшем
исходе
мы
можем
выбрать
действие,
которое
приведет
нас
к
одному
множеству
неопределенностей,
а
не
к
другому.
Подробно
разработана
теория,
которая
помогает
принять
правильное
решение
перед
лицом
неопределенности.
Эта
область
знаний
называется
теорией
полезности.
В
силу
большой
значимости
этой
теории
для
страховых
систем
мы
дадим
здесь
обзор
основных
ее
положений.
Один
из
подходов
к
решению
задачи
принятия
решения
перед
лицом
неопре
деленности
состоит
в
том,
чтобы
определить
ценность
экономического
проекта
со
случайным
исходом
как
его
среднее,
ожидаемое,
значение.
Согласно
этому
nрин
u,иnу
ожидаемого
зна'Ченu.я,
распределение
возможных
исходов
можно
заменить
в
целях
принятия
решения
одним
единственным
числом,
ожидаемым
значением
слу
чайного
исхода,
выраженным
в
денежной
форме.
Согласно
этому
принципу,
лицу,
принимающему
решения,
должно
быть
безразлично,
принять
на
себя
случайные
по
тери
Х
или
выплатить
величину
Е[Х]
с
тем,
чтобы
обезопасить
себя от
возможных
потерь.
Аналогично,
лицо,
принимающее
решения,
должно
быть
согласно
выпла
тить
сумму,
не
превышающую
величины
Е[У],
дЛЯ
того
чтобы
принять
участие
в
рискованном
предприятии
со
случайными
выплатами
У.
В
экономике
ожидаемое
значение
случайных
событий,
которые
сопряжены
с
денежными
выплатами,
часто
называется
'Ч.естноU
или
а'К:туарной
стоимостью
этого
события.
Многие
из
лиц,
принимающих
решения,
не
признают
принцип
ожидаемого
зна
чения.
Они
считают,
что
на
принимаемое
ими
решение
оказывают
влияние
размер
их
капитала
и
другие
характеристики
распределения
исходов.
Ниже
приводится
пример,
цель
которого
-
продемонстрировать
неадекватность
принципа ожидаемого
значения
с
точки
зрения
лица,
принимающего
решения
в
страховании
от
несчастных
случаев.
Во
всех
случаях
предполагается,
что
вероят
ность
наступления
несчастного
случая
равна
0,01,
а
вероятность
ненаступления
несчастного
случая
равна
0,99.
В
зависимости
от
величины
ущерба
в
результате
наступления
несчастного
случая
рассматриваются
три
варианта;
ожидаемый
ущерб
для
каждого
ИЗ
них
приведен
в
следующей
таблице:
Случай
1
2
3
Возможный
ущерб
о
1
О
1000
О
1000000
Ожидаемый
ущерб
0,01
10,00
10000,00
Возможно,
ущерб
размера
1
мало
волнует
человека,
принимающего
решения,
а
значит,
он
может
не
пожелать
платить
сумму,
большую,
чем
величина
ожидаемого
ущерба,
за
приобретение
страхового
покрытия.
Однако
ущерб
в
размере
1000000,
который
может
превышать
имеющиеся
у
него
средства,
оказался
бы
катастрофиче
ским.
В
этом
случае
человек,
принимающий
решения,
мог
бы
согласиться
заплатить
за
страхование
больше,
чем
сумма
ожидаемых
потерь,
которая
составляет
10000.
Тот
факт,
что
сумма,
которую
принимающее
решения
лицо
готово
заплатить
за
страховое
покрытие,
может
отличаться
от
ожидаемого
значения,
наводит
на
мысль,
что
для
модели
поведения
принцип
ожидаемого
значения
не
подходит.
24
Гл.
1.
Экономика
страхования
Для
того
чтобы
объяснить,
почему
лицо,
принимающее
решения,
может
согла
ситься
платить
больше,
чем
ожидаемое
значение,
мы
исследуем
другой
подход.
Сна
чала
мы
просто
предположим,
что
то
значение
полезности,
которое
рассматриваемое
лицо
связывает
с
капиталом
величины
w,
измеренной
в
долларах,
может
быть
вы
ражено
в
виде
некоторой
функции
u(
w),
называемой
фун,'к;'Цuеu
nолезностu
('lCanu-
тала).
Мы
проведем
процедуру,
которая
позволяет
определить
ряд
значений
такой
функции.
Для
этого
мы
предположим,
что
лицо,
принимающее
решения,
имеет
ка
питал
20
000.
Линейное
преобразование
u*(w) =
аu(ш)
+
Ь,
а
>
О,
определяет
функцию
и*{ш),
которая
по
существу
эквивалентна
функции
и(ш).
То
гда
с
помощью
выбора
чисел
а
и
Ь
мы
можем
произвольным
образом
определить
значение
функции
полезности,
соответствующей
предпочтениям
лица,
принимаю
щего
решения,
в
точке
О
и
еще
в
одной
точке.
Итак,
мы
полагаем
и(О)
=
-1
и
u(20 000) =
О.
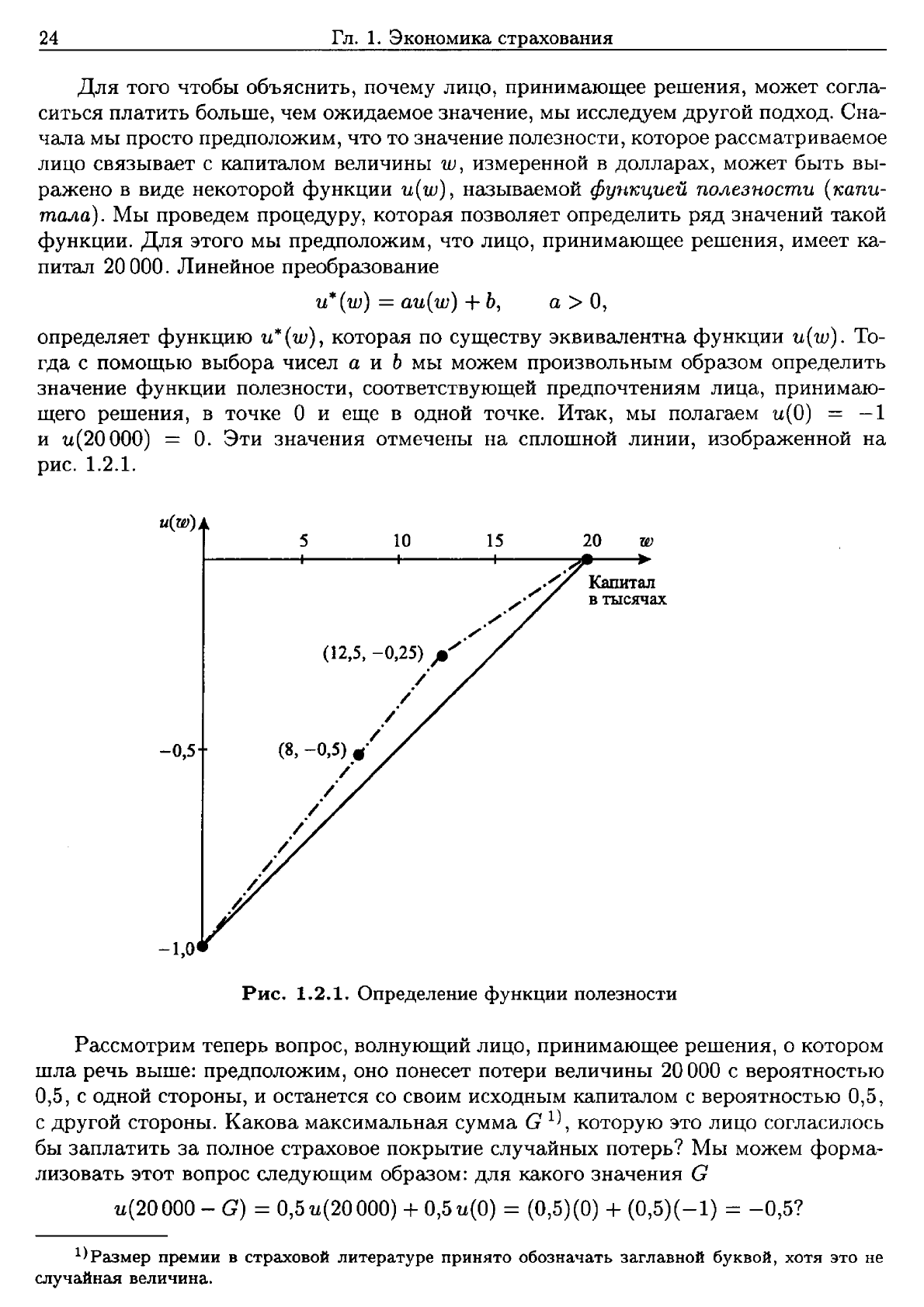
Эти
значения
отмечены
на
сплошной
линии,
изображенной
на
рис.
1.2.1.
u(w)
5
10 15
20
w
-0,5
-1,0
././
..
,.,-
./
/
/.
(12,5,
-0,25).,.
./
/
/
/
(8,
-0,5)
fI'
/
./
./
/
/
/
~
~
Капитал
в
тысячах
Рис.
1.2.1.
Определение
функции
полезности
Рассмотрим
теперь
вопрос,
волнующий
лицо,
принимающее
решения,
о
котором
шла
речь
выше:
предположим,
оно
понесет
потери
величины
20000
с
вероятностью
0,5,
с
одной
стороны,
и
останется
со
своим
исходным
капиталом
с
вероятностью
0,5,
с
другой
стороны.
Какова
максимальная
сумма
G
1),
которую
это
лицо
согласилось
бы
заплатить
за
полное
страховое
покрытие
случайных
потерь?
Мы
можем
форма
лизовать
этот
вопрос
следующим
образом:
для
какого
значения
G
и(20
000 -
а)
= 0,5
и(20
000) +0,5
u(О)
= (0,5)(0) +(0,5)(
-1)
=
-0,5?
l)Размер
премии
в
страховой
литературе
принято
обозначать
заглавной
буквой,
хотя
это
не
случайная
величина.

1.2.
Теория
полезности
25
Если
выплачивается
сумма
С,
капитал,
безусловно,
сократится
до
величины
20000 -
С.
Знак
равенства
здесь
говорит
о том,
что
лицо,
принимающее
решения,
одинаково
относится
к
тому,
чтобы
заведомо
выплатить
сумму
С,
и
к
тому,
что
ожидаемая
полезность
капитала
будет
такой,
как
в
правой
части
выписанного
выше
соотношения.
Предположим,
что
ответ
лица,
принимающего
решения,
будет
G = 12000.
Тогда
u(20 000 - 12000) =u(8000) =
-0,5.
Этот
результат
изображен
на
пунктирной
линии
на
рис.
1.2.1.
Возможно,
наибо
лее
важный
аспект
такого
ответа
состоит
в
том,
что
лицо,
принимающее
решения,
согласно
заплатить
за
страхование
сумму,
которая
превосходит
(0,5)(0) +(0,5)(20000) = 10000,
ожидаемую
величину
потерь.
Эту
процедуру
можно
использовать
для
добавления
стольких
точек
(w,
u(w))
при
О
:::;
w
:::;
20000,
сколько
необходимо
для
получения
удовлетворительного
при
ближения
к
функции
полезности
капитала.
Если
установлены
значения
функции
полезности
для
двух
величин
капитала
wl
и
W2,
где
О
:::;
Wl
:::;
W2
:::;
20000,
то
можно
определить
дополнительную
точку,
задав
принимающему
решения
следующий
во
прос:
какую
максимальную
сумму
он
готов
платить
за
полное
страховое
покрытие
риска,
что
он
останется
с
капиталом
W2
с
некоторой
вероятностью
Р,
или
с
меньшим
капиталом
Wl
с
вероятностью
1-
р?
Мы
просим
принимающего
решения
определить
такое
значение
С,
что
U(W2
-
С)
=
(1
- P)U(Wl) + PU(W2)' (1.2.1)
Если
его
устраивает
значение
W2
- G =
Wз,
ТО
точка
(Wз,
(1-
P)U(Wl) +PU(W2))
при
нимается
в
качестве
еще
одной
точки
графика
функции
полезности.
Этот
процесс
используется
для
нахождения
четвертой
точки
(12500,
-0,25)
на
графике,
изобра
женном
на
рис.
1.2.1.
Такое
выяснение
предпочтений
дает
множество
точек
на
гра
фике
функции
полезности
лица,
принимающего
решения.
По
этим
точкам
можно
построить
гладкую
функцию,
которая
имеет
вторую
производную,
и
принять
ее
в
качестве
функции
полезности
в
каждой
точке.
После
того
как
принимающий
решения
определил
свою
функцию
полезности,
применяя
описанный
выше
метод,
эта
функция
может
применяться
для
сравнения
двух
случайных
экономических
исходов.
Эти
исходы
будут
обозначаться
случай
ными
величинами
l
)
Х
и
У.
Мы
ищем
такое
прщшло
принятия
решения,
которое
будет
согласовано
с
предпочтениями,
уже
выявленными
при
определении
функции
полезности
капитала.
Так,
если
принимающий
решения
имеет
капитал
W
и
должен
сравнить
случайные
исходы
Х
и
У,
то
он
выберет
Х,
если
E[u(w +
Х)]
> E[u(w +
У)],
и
ему
будет
безразлично,
какой
из
исходов
Х
и
У
осуществится,
если
E(u(w +
Х)]
=
Е[u(щ
+
У)].
Хотя
метод
опроса
и
использования
функции
полезности
может
показаться
разум
ным,
ясно,
что
наши
неформальные
построения
должны
быть
подкреплены
более
l)Часто
для
термина
«случайная
величина.
мы
будем
использовать
сокращение
С.В.
-
При,,".
ред.

26
Гл.
1.
Экономика
страхования
строгой
цепочкой
рассуждений,
если
мы
хотим,
чтобы
теория
полезности
состави
ла
логически
последовательную
и
исчерпываюшую
основу
для
принятия
решений
перед
лицом
неопределенности.
Если
мы
хотим
понять
экономическую
роль
стра
хования,
такая
основа
необходима.
Ниже
приводится
описание
такой
более
строгой
теории.
Отправной
точкой
теории
является
предположение
о том,
что
разумный
чело
век,
сталкиваясь
с
двумя
распределениями
исходов,
влияющих
на
капитал,
суме
ет
выразить
либо
предпочтение
по
отношению
к
одному
ИЗ
этих
распределений,
либо
одинаковое
отношение
к
обоим.
Далее,
предпочтения
должны
удовлетворять
некоторым
требованиям
согласованности.
Наивысшей
точкой
теории
является
те
орема,
утверждающая,
что
если
предпочтения
удовлетворяют
требованиям
согла
сованности,
то
существует
функция
полезности
u(w),
такая,
что
если
распределе
ние
Х
предпочтительнее,
чем
распределение
У,
то
Е[u(Х)]
>
Е[u(У)]
,
а
если
при
нимающий
решения
не
отдает
предпочтение
ни
одному
ИЗ
этих
распределений,
то
Е[u(Х)]
=
Е[u(У)].
Таким
образом,
качественное
предпочтение
или
отсутствие
та
кового
можно
заменить
сравнением
чисел.
В
разд.
1.6
даны
ссылки
на
публикации,
содержащие
подробное
изложение
этой
теории.
Перед
тем
как
переходить
к
приложениям
теории
полезности
в
страховании,
выпишем
ряд
утверждений,
касающихся
полезности.
Утверждения.
1.
Теория
полезности
основана
на
предположении
о
существо
вании
и
согласованности
предпочтений
относительно
распределений
вероятностей
возможных
исходов.
Функция
полезности
не
должна
отражать
никаких
неожидан
ностей.
Она
является
численным
описанием
имеющихся
предпочтений.
2.
Функция
полезности
не
должна,
а
на
самом
деле
не
может,
определяться
единственным
образом.
Например,
если
u*(w) = au(w) +
Ь,
а>
О,
то
соотношение
эквивалентно
соотношению
Е[u(Х)]
>
Е[u(У)]
Е[u*
(Х)]
>
Е[u*(У)].
Таким
образом,
предпочтения
сохраняются,
если
функция
полезности
является
ли
нейным
преобразованием
исходной
с
положительными
коэффициентами.
Этот
факт
использовался
в
примере,
который
иллюстрировался
рис.
1.2.1,
где
две
точки
выби
рались
произвольным
образом.
З.
Предположим,
что
функция
полезности
линейна
и
ее
угол
наклона
положи
телен,
т.
е.
u(w)=aw+b,
а>О.
Тогда
если
Е[Х]
=
J-tx
и
Е[У]
=J-ty,
то
Е[u(Х)]
=
aJ.tx
+
Ь
>
Е[u(У)]
=
Щ-.tу
+
Ь
в
том
и
только
том
случае,
когда
J.tx
>
J.ty.
Таким
образом,
для
возрастающей
линейной
функции
полезности
предпочтения
относительно
распределений
исходов
упорядочены
так
же,
как
математические
ожидания
этих
распределений.
Следова
тельно,
если
функция
полезности
является
линейной
и
возрастающей,
то
принцип
ожидаемого
значения
для
рационального
экономического
поведения
перед
лицом
неопределенности
не
противоречит
правилу
ожидаемой
полезности.

1.3.
Страхование
и полезность
27
1.3.
Страхование
и
полезность
В
разд.
1.2,
чтобы
лучше
понять
экономическую
роль
страхования,
мы
описали
теорию
полезности.
Начнем
анализ
этой
роли
с
одного
примера.
Предположим,
что
лицо,
принимающее
решения,
владеет
собственностью,
которая
может
быть
повреж
дена
или
уничтожена
в
течение
следующего
отчетного
периода.
Величина
ущерба,
которая
может
равняться
О,
-
это
случайная
величина,
которая
будет
обозначаться
через
Х.
Мы
будем
предполагать,
что
ее
распределение
известно.
Тогда
величина
Е[Х],
ожидаемая
величина
ущерба
в
следующий
отчетный
период,
может
рассмат
риваться
как
долговременные
средние
потери,
если
эксперимент,
состоящий
в
том,
что
собственность
подвергается
опасности
ущерба,
может
многократно
проводиться
при
неизменных
условиях.
Ясно, ЧТО
одно
лицо,
принимающее
решения,
не
может
осуществить
такую длительную
последовательность
экспериментов.
Предположим,
что
создается
страховая
организация
(страховщих;)
,
цель
ко
торой
-
уменьшить
финансовые
последствия
повреждения
или
уничтожения
соб
ственности.
Страховщик
выпускает
контракты
(договор'ы)
,
которые
являются
обя
зательствами
выплатить
владельцу
собственности
определенную
сумму
(страховую
су,м,,м,у),
равную
или
меньшую,
чем
понесенные
финансовые
потери,
если
собствен
ность
повреждена
или
уничтожена
в
течение
периода
действия
договора.
Платежи,
обусловленные
этими
обстоятельствами
и
связанные
с
размером
ущерба,
называ
ются
страховы,м,и
8ъш.л,аmа,м,и.
В
обмен
на
обязательства,
закрепленные
в
договоре,
владелец
собственности
(страховаmе.л,ъ)
выплачивает
страховщику
вознаграждение
(nре,м,uю
).
Величина
премиальных
выплат
определяется
принципом
экономических
реше
ний,
которые
принимаются
как
страховщиком,
так
и
страхователем.
Существует
возможность
взаимовыгодного
страхового
договора,
когда
величина
премии
по
до
говору,
определяемая
страховщиком,
меньше,
чем
максимальная
сумма,
которую
владелец
собственности
готов
платить
за
страхование.
При
целом
ряде
финансовых
обстоятельств
для
отдельно
взятого
договора
стра
хования
функция
полезности
страховщика
может
приближаться
прямой
линией.
В
этом
случае
при
определении
размера
премии
страховщик
должен
руководство
ваться
принципом
ожидаемого
значения,
как
указано
в
утверждении
3
разд.
1.2.
Другими
словами,
страховщик
должен
назначить
в
качестве
базовой
премии
при
полном
страховом
покрытии
величину,
равную
ожидаемому
ущербу,
Е[Х]
=
р,.
в
этом
контексте
Jl
называется
неmmо-nре,м,uей
для
страхового
договора,
заклю
ченного
на
один
срок.
Для
того
чтобы
обеспечить
себе
средства
на
покрытие
рас
ходов
и
уплату
налогов,
а
также
некоторую
прибыль
и
чтобы
до
некоторой
степени
обезопасить
себя
от
неблагоприятной
динамики
потерь,
страховая
система
должна
при
определении
премии
по
договору
установить
надбавх;у,
которая
прибавляется
к
нетто-премии.
Например,
премия
с
надбавкой,
обозначаемая
через
Н,
может
зада
ваться
равенством
н
=
(1
+a)Jl +
с,
а>
О,
с>
О.
Можно
считать,
что
величина
ар,
в
этом
соотношении
связана
с
теми
расходами,
которые
изменяются
с
изменением
ожидаемого
ущерба,
и
с
риском
того,
что
реаль
ные
страховые
выплаты
будут
отличаться
от
ожидаемых.
Константа
с
соответствует
ожидаемым
расходам,
которые
не
зависят
от
величины
ущерба.
Ниже
мы
рассмот
рим
другие
экономические
принципы,
лежащие
в
основе
определения
премий,
кото
рые
могут
быть
приемлемыми
для
страховщика.

28
Гл.
1.
Экономика
страхования
Применим
теорию
полезности
к
проблеме
принятия
решений,
с
которой
сталки
вается
лицо,
собственность
которого
подвергается
риску.
Такой
владелец
собствен
ности
обладает
функцией
полезности
капитала
u(w),
где
капитал
w
измерен
в де
нежных
единицах.
Он
может
понести
потери
из-за
наступления
случайных
собы
тий,
которые
нанесут
вред
его
собственности.
Распределение
случайных
потерь
Х
предполагается
известным.
Как
и
в
(1.2.1),
владельцу
собственности
безразлично,
платить
ли
сумму
G
страховщику,
перекладывая
на
него
случайные
финансовые
потери,
или
принимать
риск
на
себя.
Это
положение
может
быть
формализовано
соотношением
u(w -
а)
= E(u(w -
Х)].
(1.3.1)
Правая
часть
формулы
(1.3.1)
представляет
собой
ожидаемую
полезность
при
от
казе
от
покупки
страхового
договора,
если
текущая
величина
капитала
владельца
собственности
равна
w.
Левая
часть
представляет
собой
ожидаемую
полезность
при
выплате
суммы
G
за
полное
финансовое
покрытие.
Если
функция
полезности
владельца
является
возрастающей
и
линейной,
т.
е.
u(ш)
=
bw
+
d,
Ь
>
О,
ТО
он
примет
принцип
ожидаемого
значения.
В
этом
случае
владелец
собственности
или
не
отдает
предпочтение
ни
одной
из
возможностей,
или
отдает
предпочтение
страхованию,
если
и(ш
-
а)
=
Ь(ш
-
а)
+d
~
Е(и(ш
-
Х)]
=
Е(Ь(ш
-
Х)
+
d],
b(w
-
а)
+d
~
b(w
-
J.t)
+
d,
G
~
/J.
Таким
образом, если
функция
полезности
владельца
собственности
возрастает
и
линейна,
величина
премии,
при
которой
он
не
отдает
предпочтения ни одной
из
возможностей
или
предпочитает
приобрести
полное
страховое
покрытие,
не
пре
восходит
величины
ожидаемых
потерь.
При
отсутствии
дотаций
при
долгосрочном
планировании
страховщик
должен
позаботиться
о
том,
чтобы
полученные
премии
превысили
его
ожидаемые
потери.
Поэтому
в
рассматриваемом
случае
заключение
взаимовыгодного
страхового
договора
маловероятно.
При
заключении
страхового
договора
страховщик,
для
того
чтобы
избежать
недостаточности
поступлений,
дол
жен
назначить
премию,
размер
которой
превышает
ожидаемый
ущерб
и
расходы.
Таким
образом,
функция
полезности
владельца
собственности
не
может
быть
ли
нейной.
В
разд.
1.2
отмечал
ось
,
что
для
существования
функции
полезности
необходи
мо,
чтобы
предпочтения
лица,
принимающего
решения,
обладали
определенными
свойствами
согласованности.
Хотя
эти
требования
и
не
были
перечислены, отметим,
что
они
не
содержат
никаких
положений,
в
силу
которых
функция
полезности
ока
зывалась
бы
линейной,
квадратичной,
показательной,
логарифмической
или
имела
какую-либо
другую
определенную
форму.
На
самом
деле
каждая
из
перечисленных
выше
функций
может
служить
функцией
полезности
для
некоторого
лица,
при
ни
мающего
решения,
а
функция,
составленная
из
их
сегментов,
может
отражать
предпочтения
еще
какого-то
лица.
Все
же
кажется
естественным
предполагать,
что
и(ш)
является
возрастающей
функцией,
«больше
~
лучше».
Кроме
того,
было
замечено,
что
для
многих
лиц,
принимающих
решения,
при
увеличении
капитала
равными
долями
полезность
уве
личивается
уменьшающимися
долями.
Это
отражается
в
известном
экономическом
положении
об
убывающей
предельной
полезности.
1.3.
Страхование
и
полезность
29
(1.3.2)
(1.3.3)
Приближение
функции
полезности
на
рис.
1.2.1
состоит
из
сегментов
прямых
с
положительными
коэффициентами
наклона.
Это
дает
соотношение
Д
2
и
(
w)
~
О.
(По
поводу
конечных
разностей
см.
приложение
5.)
Если
это
наблюдение
распространить
на
более
гладкие
функции,
то
мы
придем
к
следующим
двум
свойствам:
u'(w) >
О
и
и"(ш)
<
О.
Из
второго
неравенства
следует,
что
и(ш)
является
строго
выпуклой
вверх
функцией.
В
обсуждении
решений,
принимаемых
в
страховании
на
основе
строго
вьшук
лой
вверх
функции
полезности,
мы
будем
пользоваться
н.еравен.ство.м.
Ие'Н,се'Н,а.
Это
неравенство
утверждает,
что
дЛЯ
С.
в.
Х
И
функции
u(
w)
если
и"
<
О,
то
Е[и(Х)]
~
u(Е[Х]),
если и"
>
О,
то
Е[и(Х)]
~
и(Е[Х]).
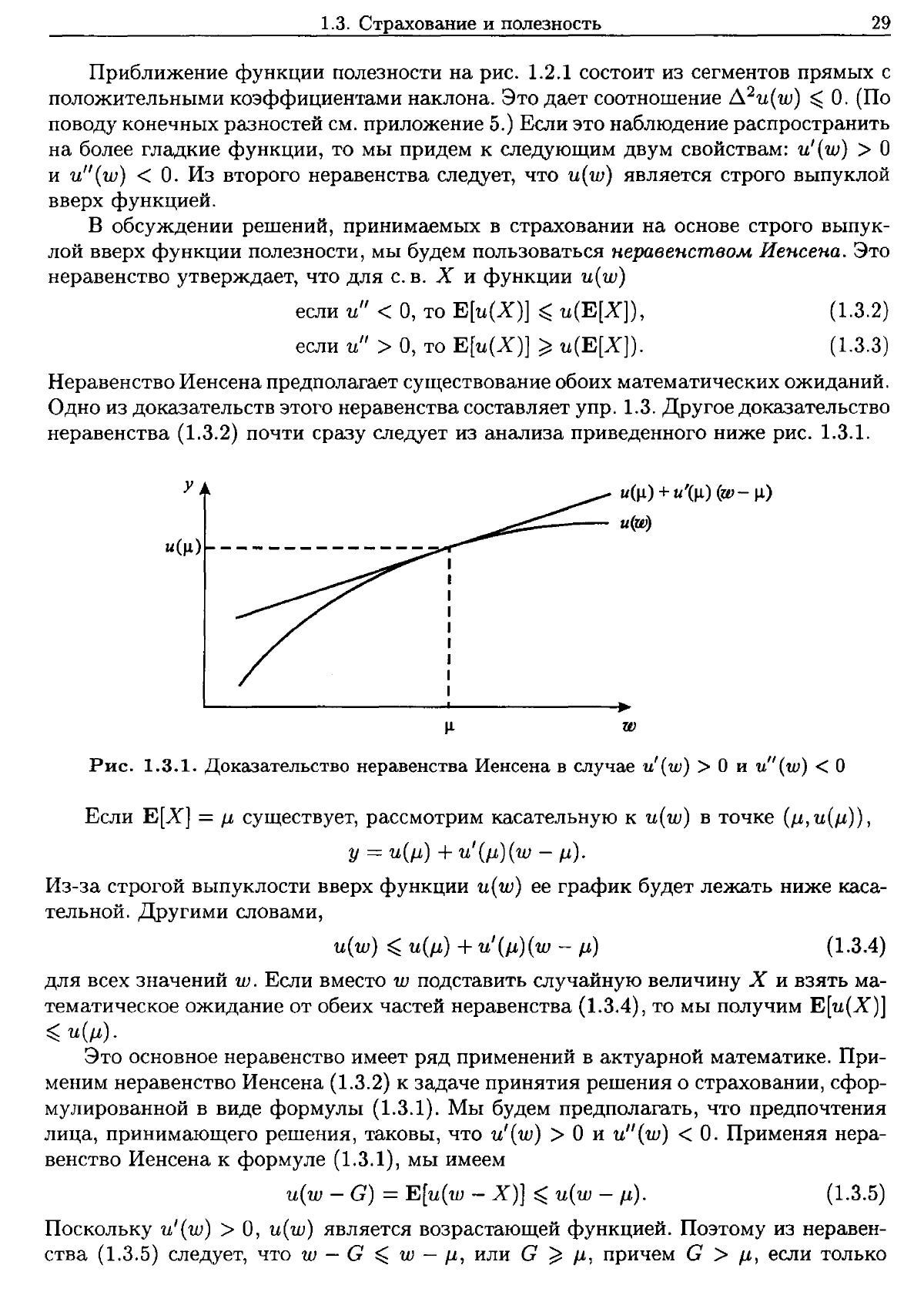
Неравенство
Иенсена
предполагает
существование
обоих
математических
ожиданий.
Одно
из
доказательств
этого
неравенства
составляет
упр.
1.3.
Другое
доказательство
неравенства
(1.3.2)
почти
сразу
следует
из
анализа
приведенного
ниже
рис.
1.3.1.
у
u(lJ.)
+
u'(lJ.)
(ш
-
lJ.)
~~_--
u(ш)
w
Рис.
1.3.1.
Доказательство
неравенства
Иенсена
в
случае
u'(w)
>
О
и
u"(w)
<
О
Если
Е[Х]
=
IJ
существует,
рассмотрим
касательную
к
u(w)
в
точке
(J..L,
U(IJ»,
у
=
и
(р)
+
и'
(J..L
)(
w -
р).
Из-за
строгой
выпуклости
вверх
функции
и(ш)
ее
график
будет
лежать
ниже
каса
тельной.
Другими
словами,
и(ш)
~
и(р)
+
u'(р)(ш
-
р)
(1.3.4)
для
всех
значений
ш.
Если
вместо
w
подставить
случайную
величину
Х
и
взять
ма
тематическое
ожидание
от
обеих
частей
неравенства
(1.3.4),
то
мы
получим
Е[u(Х)]
~
u(р).
Это
основное
неравенство
имеет
ряд
применений
в
актуарной
математике.
При
мени
м
неравенство
Иенсена
(1.3.2)
к
задаче
принятия
решения
о
страховании,
сфор
мулированной
в
виде
формулы
(1.3.1).
Мы
будем
предполагать,
что
предпочтения
лица,
принимающего
решения,
таковы,
что
и'(ш)
>
О
и
и"(ш)
<
О.
Применяя
нера
венство
Иенсена
к
формуле
(1.3.1),
мы
имеем
u(w -
С)
=
Е[и(ш
-
Х)]
~
и(ш
-
р).
(1.3.5)
Поскольку
u'(w) >
О,
u(w)
является
возрастающей
функцией.
Поэтому
из
неравен
ства
(1.3.5)
следует,
что
w - G
~
w -
IJ,
или
G
~
р,
причем
G >
р,
если
только

30
Гл.
1.
Экономика
страхования
С.В.
Х
не
является
константой.
В
экономических
терминах,
мы
установили,
что
если
u'(w)
>
О
и
u"(w)
<
О,
то
принимающий
решения
будет
платить
за
страхование
сумму,
превосходящую
ожидаемые
потери.
Если
величина
G
не
меньше
премии,
назначенной
страховщиком,
то
возможен
взаимовыгодный
страховой
договор.
Формально,
будем
говорить,
что
лицо,
принимающее
решения
на
основе
функ
ции
полезности
u(w),
'Не
с'К:ло'Н'Но
'к:
рис'К:у,
тогда
и
только
тогда,
когда
u"(w)
<
О.
Займемся
теперь
общей
функцией
полезности
для
страховщика.
Обозначим
че
рез
U/(W)
функцию
полезности
страховщика
и
через
Ш/
текущий
капитал
страхов
щика
в
денежных
единицах.
Тогда
минимальная
допустимая
премия
Н
за
взятый
на
себя
риск
Х
с
точки
зрения
страховщика
может
быть
определена
из
формулы
(1.3.6)
Ее
левая
часть
является
полезностью,
соответствующей
текущему
положению
стра
ховщика.
Правая
часть
является
ожидаемой
полезностью,
соответствующей
полу
чению
премии
Н
и
выплате
случайных
потерь
Х.
Другими
словами,
для
страхов
щика
нет
различия
между
его
текущим
положением
и
предоставлением
страхового
покрытия
от
риска
Х
при
условии
получения
премии
Н.
Если
функция
полезности
страховщика
такова,
что
и~(ш)
>
О
и
и1(ш)
<
о,
то,
воспользовавшись
неравенством
Иенсена
(1.3.2)
и
соотношением
(1.3.6),
мы
можем
получить
U/(WJ)
=
Е[и/(ш/
+
Н
-
Х)]
~
UI(W/
+
Н
- Jl).
При
меняя
те
же
рассуждения,
что и
для
формулы
(1.3.5),
мы
видим,
что
Н
~
Jl.
Если
величина
С,
определяемая
лицом,
принимающим
решения,
исходя
из
соотно
шения
(1.3.5),
такова,
что
G
~
Н
~
J..L,
страховой
договор
может
быть
заключен.
Это
означает,
что
ожидаемая
полезность
ни
для
одной
из
сторон
не
убывает.
Функция
полезности
основана
на
предпочтениях
лица,
принимающего
решения,
при
различных
распределениях
исходов.
Страховщик
-
это
не
обязательно
отдель
ное
физическое
лицо.
Это
может
быть
товарищество,
акционерное
общество
или
государственная
организация.
В
этом
случае
определение
UJ(W),
функции
полез
ности
страховщика,
может
оказаться
довольно
тяжелой
задачей.
Например,
если
страховщик
является
акционерным
обществом,
одной
из
обязанностей
правления
является
выработка
логически
последовательного
множества
предпочтений
относи
тельно
ряда
рискованных
предприятий.
Эти
предпочтения
могут
включать
компро
миссы
между
не
совпадающими
позициями
по
отношению
к
риску
разных
групп
акционеров.
Для
иллюстрации
свойств
функций
полезности
используется
ряд
элементарных
функций.
Мы
рассмотрим
сейчас
показательную,
степенную
с
дробным
показателем
и
квадратичную
функции.
Примеры
1.6,1.8,1.9,
1.10(Ь)
и
1.13
относятся
к
логариф
мической
функции
полезности.
По'К:азател'Ь'На.я
(или,
иначе,
э'К:сnо'Нен:цuал'Ь'На,я)
фУ'Н'К:'ЦU,я
nолез'Н,ости
имеет
вид
u(ш)
=
_e-a:w
для
всех
W
и
для
некоторого
фиксированного
а
>
О
и
обладает
рядом
привлекательных
свойств.
Во-первых,
и'(ш)
=ae-a:w >
О.
Во-вторых,

1.3.
Страхование
и
полезность
31
G =
lnMx(a)
о:
Поэтому
u(
w)
может
использоваться
в
качестве
функции
полезности
для
лица,
не
склонного
к
риску.
В
третьих, заметив,
что
мы,
ПО
сути
дела,
нашли
производящую
функцию
моментов
с.в.
Х.
в
предыдущей
формуле
обозначает
производящую
функцию
моментов
С.в.
Х.
в
четвертых,
страховые
пре
мии
не
зависят
от
капитала
лица,
принимающего
решения.
Для
проверки
этого
утверждения
следует
подставить
показательную
функцию
полезности
в
формулу
(1.3.1).
Тогда
_e-a(w-G)
=
E[_e-a(w-X)],
и
G
не
зависит
от
w.
Проверка
для
страховщика
осуществляется
подстановкой
показательной
функ
ции
полезности
с
параметром
Q]
в
(1.3.6):
н
=
ln
М
х
(0:]) .
Q]
Пример
1.3.1.
Функция
полезности
лица,
принимающего
решения,
имеет
вид
u(w) =
_e-
5w
.
Для
принимающего
решения
имеется
две
случайные
экономические
возможности.
Первая
из
них,
обозначаемая
через
Х,
имеет
нормальное
распределе
ние
со
средним
5
и
дисперсией
2.
Впредь,
говоря
о
нормальном
распределении
со
средним
J.L
и
с
дисперсией
(72,
мы
будем
пользоваться
сокращенной
записью
N(p" (
2
).
Другая
возможность,
обозначаемая
через
У,
имеет
распределение
N(6,
2,5).
Какую
возможность
следует
предпочесть?
Решение.
Имеем
Е[и(Х)]
=
Е[_е-
БХ
]
=
-М
Х
(
-5)
=
_e[~5(s)+(s2)(2)j2]
=
-1,
Е[и(У)]
=
Е[
-е~БУ]
=
-Му
(-5)
=
_e[-5(6)+(5
2
)(2,S)j2]
=
_e
1
,25.
Таким
образом,
Е[u(Х)]
=
-1
>
Е[и(У)]
=
_е
1
,25,
и
распределение
С.в.
Х
предпочтительнее
распределения
с.в.
У.
...
в
примере
1.3.1
С.в.
Х
предпочтительнее,
чем
У,
несмотря
на
то,
что
J.1x
= 5 <
J.1y
=
б.
Поскольку
принимающий
решения
не
склонен к
риску,
тот
факт, что
распре
деление
с.в.
У
более
«размазано~,
чем
распределение
С.в.
Х,
свидетельствует
против
распределения
С.в.
У
при
оценке
его
желательности.
Если
с.в.
У
имеет
распределе
ние
N(б,
2,4),
то
Е[и(У)]
=
-1
и
для
принимающего
решения
будет
безразлично,
выбрать
распределение
Х
или
распределение
У.
Семейство
cmeneH'J-t'ЬtХ
с
дроБН'Ьt.м
nох:азателе.м
фУН'К:'ЦUЙ
полезности
задается
соотношением
u(w) =
w'Y,
w >
О,
0<,
<
1.
Элемент
этого
семейства
может
представлять
предпочтение
лица,
не
склонного
к
риску,
поскольку
u'(w) =
,w'Y-
1
>
О
и
u"(w) =
,(,
- 1)w'Y-
2
<
О.
