Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

231

Частина 8. Диференціальне числення функцій однієї змінної

При

1000x



та

3000x 

маємо



1000 10 1 10 0,3679 1 2,679Pe





  



3000 10 1 10 0,0498 1 0,502Pe





  

Отже, при витратах на рекламу 3000 гривень прибутки спадають.



Приклад 6. Нехай валовий продукт деякої держави змінюєть!

ся з часом

за формулою

100



(мільярдів гривень),

а кількість населення змінюється за законом

120 2



(мільйонів).

Знайти швидкість зміни частини валового продукту держави, що

припадає

на кожного громадянина.



Розв’язання. Позначимо через



частину валового продук!

ту держави, що припадає на кожного громадянина.

За умовою цього прикладу



100

120 2







(тисяч гривень на одну особу).

Використовуючи механічний зміст похідної та правило диферен!

ціювання частки, знаходимо шукану швидкість



  



100 120 2 100 120 2

120 2

tttt



    











1120 2 2100

120 2

 





 

222

120 2 200 2 80 20

4 60 4 60 60

ttt

   





Отже, частина валового продукту кожного громадянина з часом

зменшується

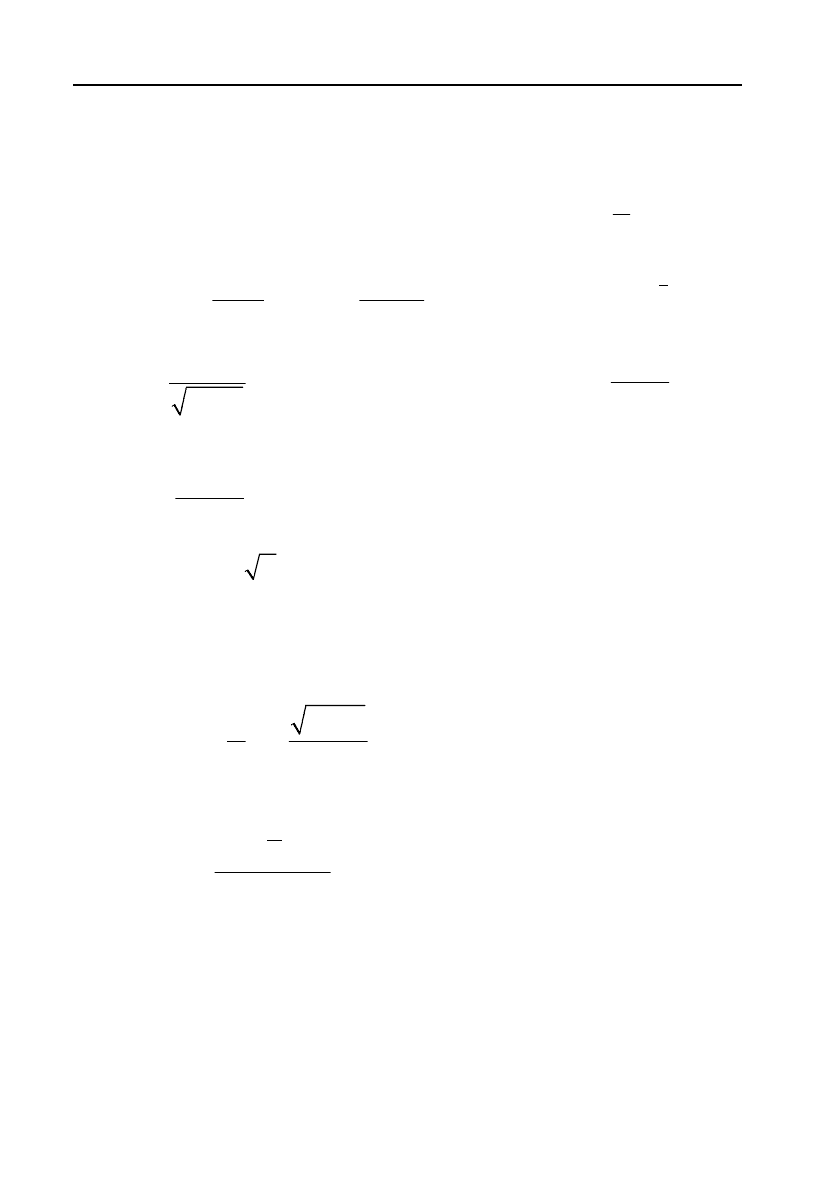
232

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

8.2.5. Вправи до розділу 8.2

1. Знайти похідні першого порядку заданих функцій

)



(1) 3yx x

 

; b)



5uy y



 





;

с)









;d)







;e)



21ux



;





;g)





;h)













Знайти диференціали першого порядку функцій

1tg







;b)

sin 2



;c)

cos



;

lnctg

x

;e)



sin

ye

;f)

3arctg



;

arcsin2

xx

Знайти границі функцій при



а)

















;



















;





23:23

xx xx



 



;



xexx







233

Частина 8. Диференціальне числення функцій однієї змінної

4. Знайти похідні першого порядку функцій, заданих неявно та

параметрично

sin cos 0

xyy

x

;b)

exy



;

ln 2 ln 0xy y x



;d)

ln ln

xx yxy



;

lncos

1lnsin











;f)

2sin2

sin

xt t











;















;h)

ctg

cos















Розв’язати задачі з економічним змістом, використовуючи по!

хідну.

а) Знайти маргінальний доход підприємства, якщо кількість ви!

готовлених та проданих виробів

та роздрібна вартість кожного

виробу

зв’язані рівністю

4000 2

p

Розв’язати задачу а) при умові, що

4000 10

p

с) Функція витрат підприємства має вигляд



2000 10 0,1 0,002Vx x x x

(тисяч гривень).

Знайти маргінальні витрати при

50x



100x



та

120x



8.3. Похідні вищих порядків

8.3.1. Поняття похідних

+го порядку

Нехай

функція



fx

визначена та має похідну першого по!

рядку в інтервалі



,ab

. Тоді її похідна







також буде функ!

цією, що визначена в



,ab

. Можна чекати, що ця функція





має

похідну

в деякій точці

інтервалу



,ab

. Таку похідну називають

234

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

другою похідною або похідною другого порядку функції



x

в точці

і позначають





або

 

або

Аналогічно визначають похідні третього, четвертого порядків.



Означення 6. Нехай

= 1, 2, 3,... Якщо функція



fx

має

похідну



1n 

порядку, диференційовану в деякій точці

інтервалу



,ab

, то похідну від





називають похідною

&го порядку і

позначають

так:



, або

Згідно з цим означенням n похідна функції



x

визначаєть!

ся рівністю

  

1nn















. (16)

Похідні вищих порядків мають широке застосування.

Так, якщо функція



SSt

описує закон руху матеріальної

точки

, то її перша похідна





дає величину миттєвої швидкості, а

друга

похідна





дорівнює швидкості зміни швидкості, тобто це

прискорення в момент

Якщо



є функція виробничих витрат (витрати на виготов!

лення

виробів), то





дає маргінальну вартість, тобто витрати

на

досить малу частину виготовлення додаткової продукції. Друга

похідна





дає швидкість зміни маргінальної вартості відносно

змін

кількості випуску продукції.

235

Частина 8. Диференціальне числення функцій однієї змінної



Приклад 7. (Аналіз функції витрат). Для функції витрат



0,001 0,3 40 1000Vx x x x

маргінальна вартість буде



0,003 0,6 40Vx x x





друга похідна має вигляд

  

0,006 0,6 0,006 100Vx x x



 

Коли

150x



маємо:



150 17,5V





;



150 0,3V





Остання рівність означає, що кожна додаткова одиниця виробле!

ної продукції спричиняє зростання на 0,3 маргінальної вартості.



Приклад 8. Знайти похідну першого та вищих порядків

функції

432

3571yx x x





Розв’язання. Шляхом послідовного диференціювання знаходимо:

12 15 14

xxx





36 30 14yxx







72 30yx



72y 

Для



маємо



y 

Вкажемо декілька формул, які використовуються при знаходженні

похідних

порядку





sin sin

xxn











(17)



cos cos

xxn











(18)



  

nnn

uv y u v

   

(19)

236

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



       



12 33

12 3

...

nn n n

nn n

uv u v Cu v Cu v Cu v

 



   



(20)

де



mnm





8.3.2. Вправи до розділу 8.3

1. Знайти похідні усіх порядків функції

532

37412yx x x



Знайти



, якщо





Знайти



, якщо







Знайти маргінальну вартість та швидкість її зміни відносно

кількості

виробів для функції витрат



500 30 0,1 0,002Vx x x x 

8.4. Основні теореми диференціального числення

Застосування похідних під час дослідження функції базується на

слідуючи

теоремах, що доведені математиками Франції у XVII та

XVIII століттях.



Теорема Лагранжа (про скінчений приріст функції). Якщо

функція



fx

неперервна на





,ab

і має похідну в усіх точ

ках інтервалу



,ab

, то всередині цього інтервалу існує хоча б

одна точка







така, що виконується рівність

 



fb fa











. (21)

237

Частина 8. Диференціальне числення функцій однієї змінної

Дамо геометричне дове!

дення цієї теореми. Прове!

демо січну

до графіка



x

(див. мал. 2) і буде!

мо пересувати цю січну пара!

лельно самій собі, поки вона

не

стане дотичною до графіка

функції

в деякій точці

з аб!

сцисою



. Відмітимо, що до!

тичну до графіка функції

можна

провести в кожній

точці

, що лежить всередині





,ab

, тому що за умовою теореми функція має похідну в усіх точ!

ках



,ab

Кутовий коефіцієнт дотичної дорівнює кутовому коефіцієнту

січної

, а саме

 

bfa

Nba







Але, згідно з геометричним змістом похідної, кутовий коефіцієнт

дотичної

до графіка функції в точці

дорівнює







. Одержимо

рівність

 



fb fa











що і треба було довести.

Рівність (21) називають формулою Лагранжа. Її можна записа!

ти у вигляді

   





 

, (22)

і тоді доведену теорему можна сформулювати так: скінчений приріст

диференційованої

функції на відрізку дорівнює відповідному приросту

y = f(x)



Мал. 2.

238

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

аргументу, помноженому на значення похідної функції в деякій

внутрішній

точці відрізка.



Теорема Ролля (про нулі похідної). Якщо функція



x

неперервна на відрізку





,ab

, диференційована в усіх внутрішніх

точках цілого відрізка, а на його кінцях приймає рівні значення,

то похідна





дорівнює нулю хоча б в одній внутрішній точці







цього відрізка.

Доведення

. Якщо



fx неперервна на





,ab

і диференційована в

усіх

внутрішніх точках, тоді для



, згідно з теоремою Лагранжа,

має місце рівність (22). За умовою теореми Ролля

 

fb fa

, тому

одержуємо



0baf





 

Але



, тому

0ba



і з останньої рівності випливає, що









. Теорема доведена.

Теорема Ролля має простий геометричний зміст: якщо функція

задовольняє

умовам теореми Лагранжа і приймає рівні значення на

кінцях

відрізка, то знайдеться хоча б одна точка, в якій дотична до

графіка

функції буде паралельна осі абсцис.



Правило Лопіталя. Нехай



та



– неперервні та

мають похідні в усіх



з околу точки



, а в точці

рівні нулю або нескінченності. Тоді границя відношення функцій

дорівнює границі відношення їх похідних, якщо остання існує,

тобто



lim lim

xa xa

fx f x

gx g x









. (23)

239

Частина 8. Диференціальне числення функцій однієї змінної

8.5. Оптимізація та побудова графіка функції

При дослідженні функції, заданої аналітично, важливо визначи!

ти її інтервали зростання, спадання, опуклість графіка функції, при

яких

функція має найбільше та найменше значення і т.д. Нижче

буде

показано, що розв’язання цих питань значно спрощується, якщо

застосовувати

похідну.

8.5.1. Зростання, спадання та екстремуми функції



Означення 7. Функцію



x

називають зростаючою

(спадною) в проміжку



,ab

, якщо більшому значенню аргументу

цьому проміжку відповідає більше (менше) значення функції, тобто

якщо

із нерівності



випливає нерівність

 

fx fx

, то

Якщо

відношення





знову є невизначеністю вигляду

або



і похідні





та





задовольняють умовам правила Лопі!

таля, то для обчислення границі можна застосувати правило Лопіта!

ля вдруге і т.д.



Приклад 9. Обчислити

lim





Розв’язання. Уданому випадку



xx

та



xe

задо!

вольняють умовам правила Лопіталя. Відношення їх є невизначеність

вигляду



при



. Застосувавши правило Лопіталя, одержуємо:

366

lim lim lim lim 0

xxxx

xx xx

xxx

eeee

   



240

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

функція



– зростаюча,

а якщо

 

x

, то

функція



спадна.

На малюнку 3 бачимо,

що в



,ab

функція



–

зростаюча, а



– спад!

на.

Необхідна ознака зростання (спадання) функції

Якщо

диференційована функція зростає (спадає) в деякому про!

міжку, то похідна цієї функції невід’ємна (недодатна) в цьому проміжку.

Доведення. Нехай



– диференційована функція і зростає в



,ab

. Згідно з означенням похідної





lim

xxfx



 







Якщо

та

xx

належать



,ab

, то в силу зростання функції



fx

знаки приросту функції та приросту аргументу однакові.

Тому



fx x fx

 





, при



Оскільки границя додатної величини не може бути від’ємною,

тому переходом до границі в цій нерівності одержимо



0fx





(x) f

(x)

Мал. 3.