Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


251
Частина 8. Диференціальне числення функцій однієї змінної
8.5.5. Загальна схема дослідження функції і побудови її графіка
Графік
заданої функції можна будувати по довільних точках. Для
цього
обирають довільним чином деяку кількість точок. Чим більше
кількість
обраних точок, тим точніше буде зображено графік функції.
Одержані вище результати дозволяють спростити цю задачу
шляхом
обирання не довільних точок, а характерних саме для зада!
ної функції.
Для науково обґрунтованого дослідження функції та побудови її
графіка
доцільно дотримуватись такої схеми:
Перший етап (використання виду заданої функції)
1.
Знаходимо область визначення функції, точки розриву, інтер!
вали неперервності.
2.
Досліджуємо функцію на парність чи непарність, періодичність.
3.
Знаходимо асимптоти графіка функції.
4.
Знаходимо точки перетину графіка функції з осями координат.
Якщо
0k
, то за формулою (26) одержимо
lim
x
bfx
, (27)
і пряма
y
b
буде горизонтальною асимптотою.
Приклад 13. Знайти асимптоти кривої
x
y
xe
.
Розв’язання. Задана функція не має точок розриву другого роду,
тому крива не має вертикальних асимптот.
Рівняння похилої асимптоти будемо шукати використовуючи
формули
(25) та (26). Маємо:
1
lim lim 1 1
x
x
xx
xe
k
xxe
.
При
x
не має скінченної границі, тобто
k
не існує.
lim lim 0
xx
xx
bxexe
.
Отже, крива
x
y
xe
має при
x
похилу асимптоту
y
x
.

252
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Другий етап (використання похідної першого порядку)
5.
Знаходимо критичні точки першого роду, інтервали зростання
та
спадання функції, точки екстремумів та екстремальні значення
функції
.
Третій етап (використання похідної другого порядку).
6.
Знаходимо критичні точки другого роду, інтервали опуклості
та
угнутості графіка функції, точки перегину та значення функції в
точках
перегину.
Четвертий етап.
7. Згідно з результатами дослідження будуємо у системі коорди!
нат отримані точки, асимптоти і будуємо графік функції з урахуван!
ням інтервалів неперервності, зростання та спадання, опуклості та
угнутості
, асимптот графіка.
Приклад 14. Дослідити функцію
2
21
1
x
y
x
та побудувати її
графік
.
Розв’язання. Задана функція має розрив в точці
1x
, тому
,1 1,
область неперервності цієї функції.
Задана функція не буде парною або непарною.
Знайдемо асимптоти графіка функції. Однобічні границі функції
в
точці розриву будуть
2
10
21
lim
1
x
x
x
,
2
10
21
lim
1
x
x
x
.
Отже, пряма
1x
є вертикальна асимптота. Перевіримо, чи має
ця
функція похилі асимптоти:
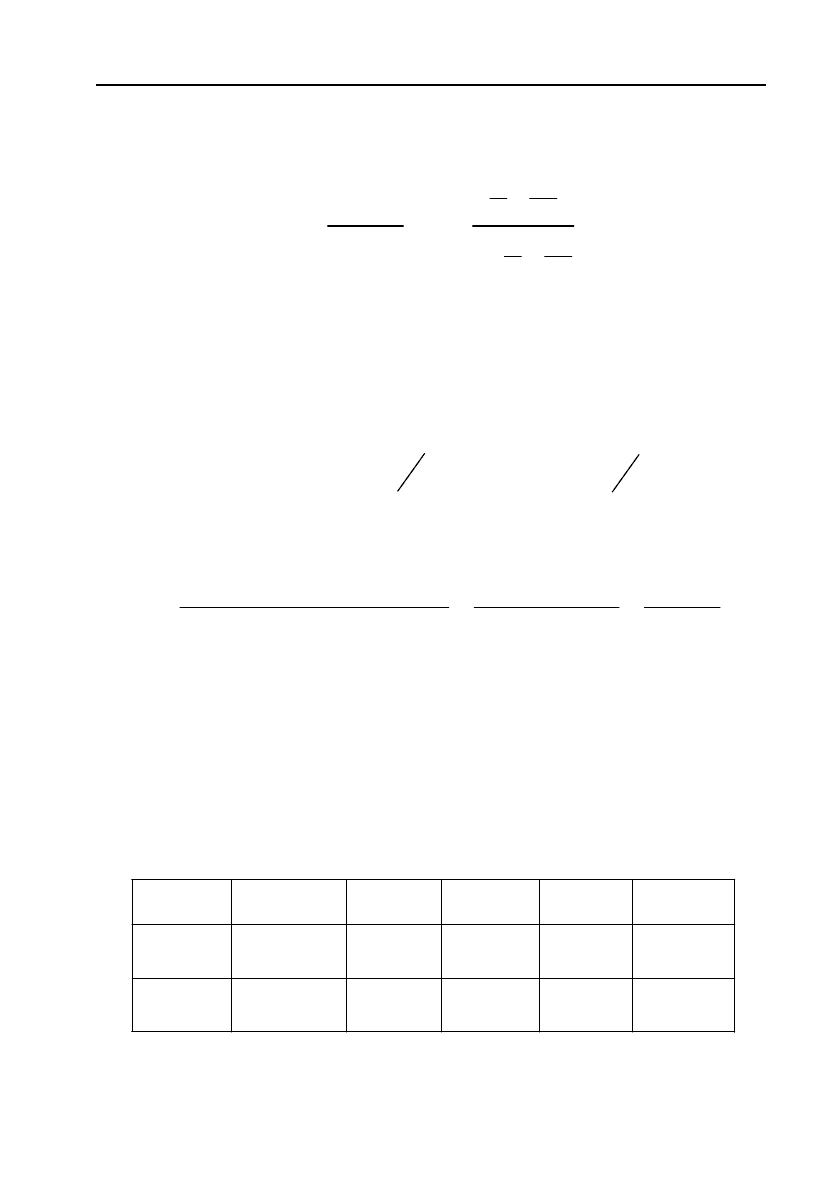
23
2
2
21
21
lim lim 0
21
1
1
xx
x
xx
k
xx
x
x
.
253
Частина 8. Диференціальне числення функцій однієї змінної
Отже, похилих асимптот не має. Шукаємо горизонтальні асимп!
тоти:
2
2
2
21
21
lim lim 0
21
1
1
xx
x
xx
b
x
x
x
.
Тому пряма
0
y
буде горизонтальною асимптотою.
Тепер знайдемо точки перетину графіка функції з осями коорди!
нат:
при
0x
маємо
1
y
, тобто точку
0
0, 1M
;
при
0
y
одержуємо
1
2
x
; тобто точку
1
1
,0
2
M
.
Переходимо до другого етапу дослідження.
Похідна функція буде
2
433
222121
2242 2
111
xxx
x
xx
y
xxx
.
Похідна не існує в точці
1
x
і дорівнює нулю при
0
x
. Отже,
критичною точкою першого роду буде лише точка
0x
тому, що
1x
не належить області визначення функції.
Складемо таблицю з врахуванням точки розриву та критичної
точки
.
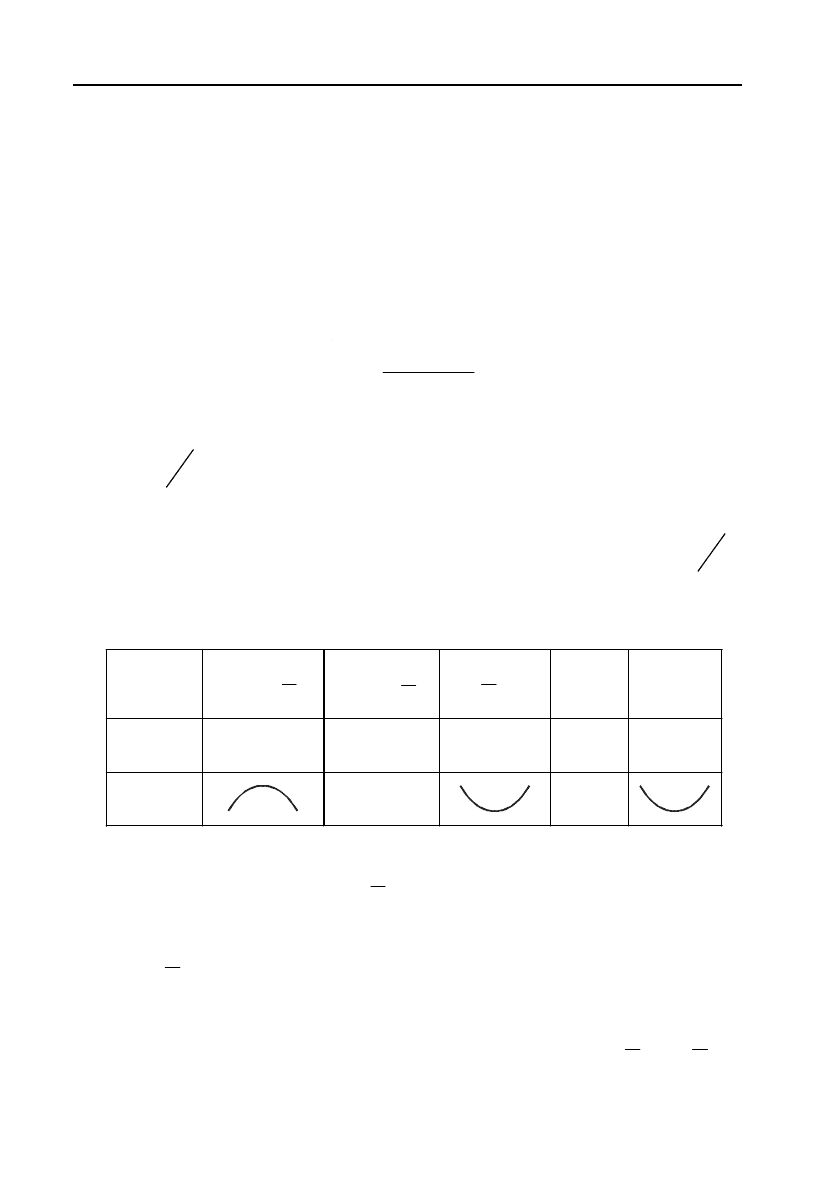
Таблиця 3
x
,0
0x
0, 1
1x
1,
fx
–
0
не
існує
–
fx
min
не
існує
254
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Отже, на інтервалі
0, 1
функція зростає, а в інтервалах
,0
та
1,
– спадає.
Екстремальним значенням функції буде
min
01yf
.
Знайдемо інтервали опуклості та угнутості графіка, точку пере!
гину за відповідною схемою: друга похідна має вигляд
4
2(2 1)
(1)
x
y
x
.
Звідси знаходимо критичні точки другого роду:
1
2
x
та
1x
, але точка
1x
не належить області визна!
чення функції.
Складаємо таблицю з врахуванням точки розриву та
1
2
x
.
Таблиця 4
Отже
, на інтервалі
1
,
2
графік функції опуклий, а в інтер!
валах
1
,1
2
та
1,
графік угнутий.
Значення функції в точці перегину буде
18
29
пер
yf
.
x
1
,
2
1
2
x
1
,1
2
1x
1,
fx
0
не
існує
fx
точка
перетину
не
існує
255
Частина 8. Диференціальне числення функцій однієї змінної
8.5.6. Вправи до розділу 8.5.
1. Знайти інтервали зростання, спадання та екстремуми функції:
a)
2
23yx x
; b)
2
x
y
x
; c)
43 2
3
97
4
yxxx
;
d)
2
2ln
y
xx
; e)
2
2
12fx x x
; f)
3
34yx x
.
2.
Знайти асимптоти графіка функції:
a)
2
63
3
xx
fx
x
; b)
2
1
45
fx
x
x
; c)
2
21
x
y
x
.
3.
Знайти інтервали опуклості, угнутості та точки перегину
функції
:
a)
1
3fx x
;b)
32
535yx x x
;
c)
54
354yx x
.
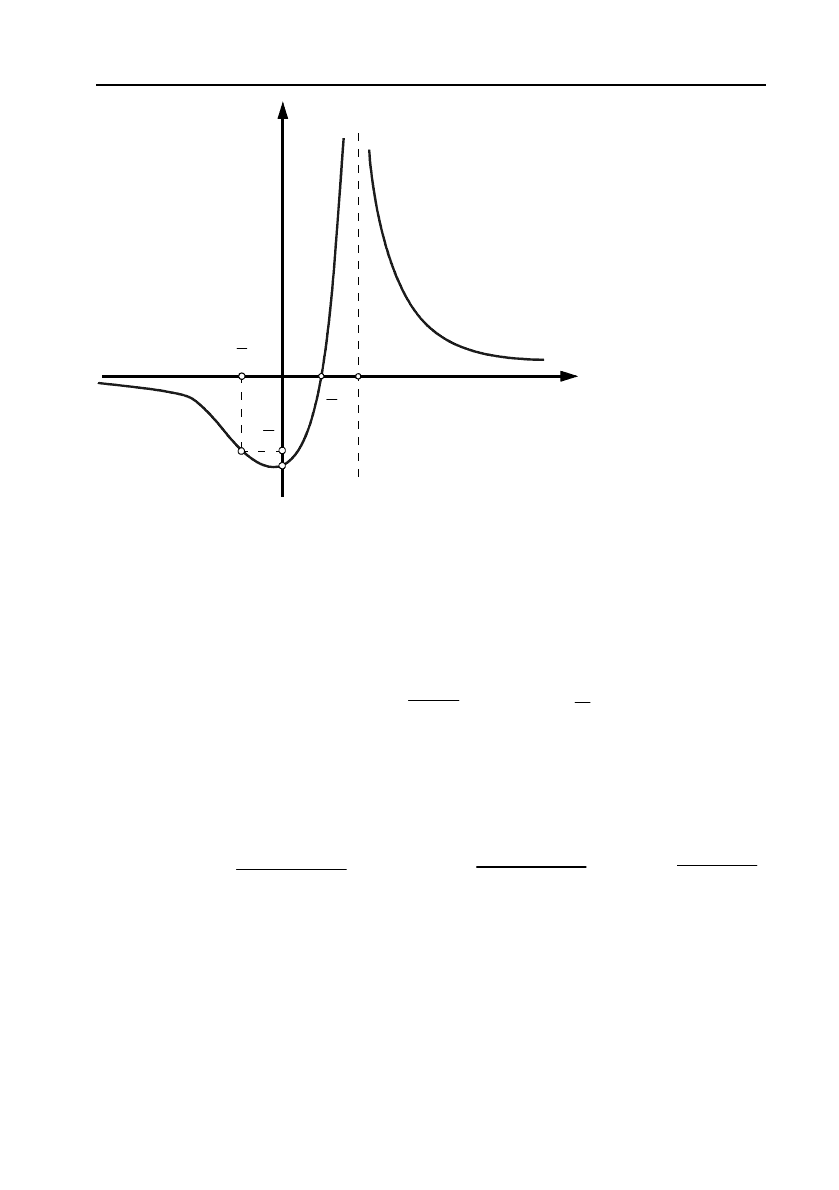
Мал. 8.
Y
X
0
1
1
2
–1
1
2
8
9
За одержани!
ми результатами
будуємо
графік
заданої
функції
(мал. 8).

256
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
4. Знайти найбільше та найменше значення функції на відрізку
,ab
:
a)
32
39
y
xxx
,
4; 4
;
b)
32 2
23121yx x x
,
1; 5
;
c)
2
6
13
x
fx
x
,
5; 5
; d)
2
3
7
x
fx
x
,
3; 7
;
e)
2
5
11
x
y
x
,
3; 7
; f)
2
4
9
x
fx
x
,
4; 6
.
5.
Розв’язати задачі:
а) Треба виготовити відкритий циліндричний бак об’єму V. Ма!
теріал, з якого виготовляють дно бака коштує
1
p
гривень за м
2
, а
вартість
матеріалу бокової поверхні –
2
p
за м
2
. При якому співвідно!
шенні радіуса дна до висоти витрати на матеріал будуть наймен!
шими?
b)
Полотняний намет об’єму V має форму прямого кругового
конуса
. При якому відношенні висота конуса до радіуса основи по!
трібна найменша кількість полотна для намету?
с) Аналіз функції витрат. Функція витрат виробництва має
вигляд
32
0,001 0,3 40 1000Vx x x x
.
Знайти, як змінюється маргінальна вартість на кожну одиницю
продукції
при
150x
.
d)
Аналіз функцій витрат, доходу та прибутку. Для функції
витрат
500 20Vx x
і заданої вартості одиниці продукції
100
p
x
, знайти інтервали, в яких функції витрат, доходу та
прибутку
зростають та спадають.

257
Частина 8. Диференціальне числення функцій однієї змінної
8.6. Один з прикладів економічного використання похідної
Розглянемо ще одне із можливих використань похідної в еконо!
мічних задачах.
8.6.1. Поняття еластичності попиту
В
багатьох задачах суттєву роль грає еластичність попиту. Оз!
найомимось з поняттям еластичності та деякими застосуваннями її.
Нехай
p
– вартість одного виробу, а
x
– кількість виробів, що
виготовлена
та продана за деякий певний інтервал часу. Нехай
xf
p
. Еластичність попиту позначають літерою
(ета) і визна!
чають так:
p
fp
pdx
xdp fp
. (28)
Дамо пояснення еластичності попиту
. Якщо вартість виробу
зросте
з
p
до
p
p
, тоді і кількість виробів також зміниться на
величину
xfp p fp
. Відносний приріст вартості буде
p
p
, а відносний приріст функції попиту буде
x
x
. Якщо відносний
приріст
помножити на 100, то одержимо відповідний відсоток змін
початкової
вартості та початкового попиту.
Наприклад, початкова вартість одного виробу 2 гривні зросла до
2,1 гривень, тоді
2,1 2 0,10
p
гривні. Отже, відносна вартість
0,05
p
p
вказує зростання початкової вартості. Якщо цю величи!
ну помножити на 100, то одержимо відсоток зміни початкової вар!
тості кожного виробу:
100 100 0,05 5%
p
p
.
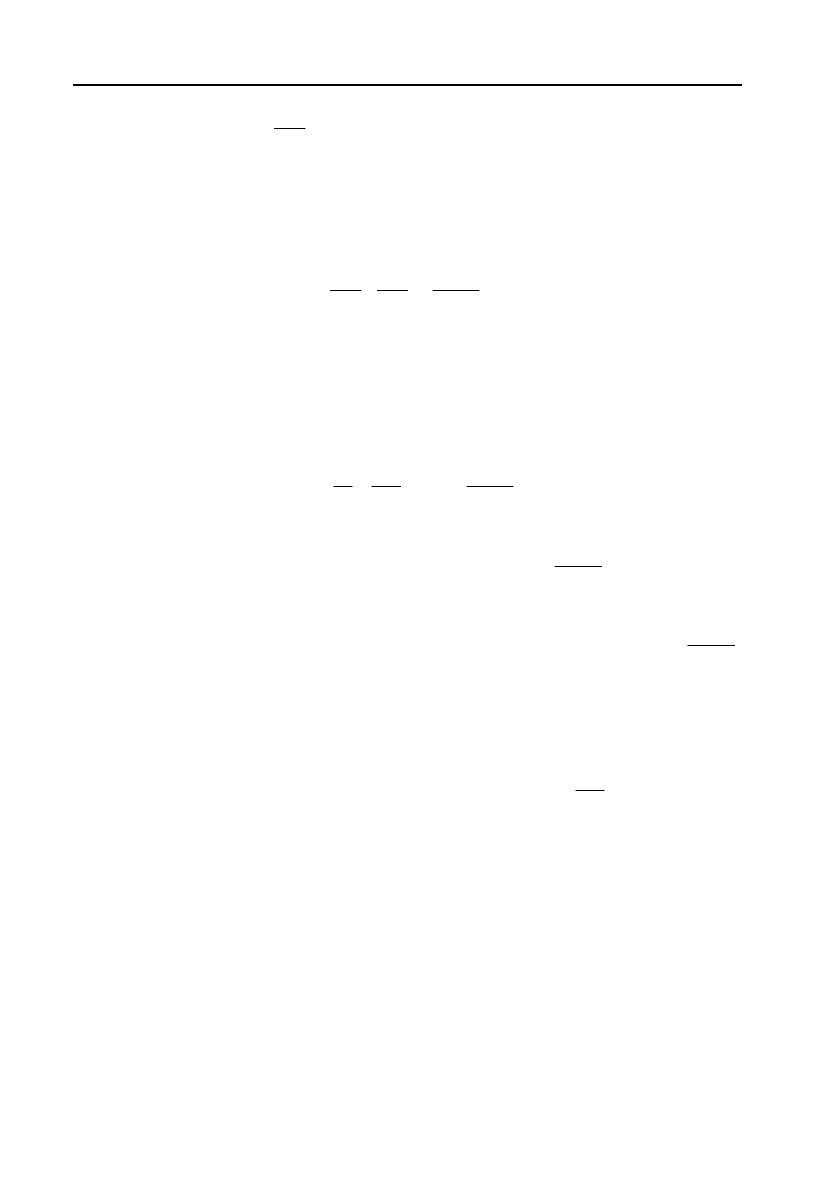
258
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Аналогічно
100
x
x
дорівнює відсотку зміни початкового попи!
ту. Якщо зростання вартості
p
викликає спад попиту, тоді
0x
.
Розглянемо відношення відносного приросту попиту до віднос!
ного приросту вартості одиниці продукції
:
x
ppx
x
pxp
.
Це співвідношення показує, в скільки разів відносний приріст
попиту
більше відносного приросту вартості кожного виробу.
Якщо в останній рівності перейти до границі при
0
p
, то
одержимо
:
0
lim
p
p
dx p x
xdp xp
.
Оскільки границя
відрізняється від виразу
p
x
xp
на нескінчен!
но малу більшого порядку малості відносно
0
p
, то
px
x
p
,
або відсоток зміни попиту
. (Відсоток зміни вартості).
Наприклад, якщо зростання вартості на
2%
викликає спадання
попиту
на
3%
, тоді еластичність попиту буде
3
1, 5
2
.
Якщо еластичність попиту
0,5
, тоді
4%
зростання вартості
викликає
зміну попиту на
(
0,5
)
4% 2%
.
Означення 14. Якщо відсоток зміни попиту більше відсотка
зміни
вартості
1
, тоді попит називають еластичним. Якщо
відсоток
зміни попиту менше відсотку зміни вартості
10
,
тоді попит називають не еластичним. Якщо
1
, то попит на&
зивають адекватним вартості одиниці вибору.

259
Частина 8. Диференціальне числення функцій однієї змінної
Поняття еластичності можна застосувати і до інших функцій
економічного
змісту.
Узагальнення формулюється так.
Нехай задана функція
y
fx
. Будемо називати
x
x
віднос!
ним приростом аргументу, а
y
y
– відносним приростом функції.
Якщо існує похідна функції
yf
x
, тоді існує границя
00 0
lim : lim lim
xx x
yx x y x yxdyx
f
x
yx y x y xydxy
,
яку називають еластичністю функції
y
fx
відносно змінної
x
і позначають
x
E
y
.
Отже, еластичність
x
xdy
Ey
y
dx
. (29)
Ця еластичність є наближений відсоток приросту функції (зрос!
тання або спадання), відповідний приросту незалежної змінної на
1%
.
Приклад 15. Встановити зв’язок між доходом підприємства та
еластичністю попиту.
Розв’язання. Функція доходу підприємства
D
xxp
,
де
x
– кількість виготовлених та проданих виробів,
p
– вартість кож!
ного виробу. Маргінальний доход відносно вартості буде
11
dD x
ddxpdx
xp x p x x
dp dp dp x dp
. (30)

260
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Якщо попит еластичний, то
1
, тому
10
і з формули
(30) випливає, що
0
dD
dp
, тобто доход
D
, який розглядають як
функцію
вартості
p
, спадає.
Якщо попит не еластичний, то
10
, тоді
10
і
0
dD
dp
.
Отже, у цьому випадку доход
D
зростає.
Якщо попит адекватний вартості, то
1
,
10
і
0
dD
dp
,
тобто доход не змінюється.
8.6.2. Вправи до розділу 8.6
Задано
зв’язок між кількістю виготовлених та проданих виробів
x
та вартістю кожного виробу
p
.
Треба:
a)
визначити еластичність попиту при
12
p
. При зростанні вар!
тості на
8,5%
знайти наближене значення відсотку зміни попиту.
2
250 30
x
pp
.
b)
При
250 0,5
p
x
і
0250x
показати, що попит на
x
еластичний і функція доходу спадає, а також показати що при
250 500x
функція попиту не еластична і доход підприємства
зростає
.
