Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

241

Частина 8. Диференціальне числення функцій однієї змінної

Тим самим твердження ознаки доведено у випадку зростання

функції

У випадку спадної функції доведення аналогічне. У цьому ви!

падку прирости функції та аргументу мають різні знаки, тому



fx x fx

 







0fx





що і треба було довести.

Достатня ознака зростання (спадання) функції

Якщо

похідна диференційованої функції додатна всередині дея!

кого проміжку, то функція зростає в цьому проміжку.

Якщо похідна диференційованої функції від’ємна всередині дея!

кого проміжку, то функція спадає в цьому проміжку.

Доведення. Нехай



0fx





при

axb

. Для довільних



, що належать



,ab

, згідно з теоремою Лагранжа маємо

   

2121

fx fx x x f







де





, а тому



,ab





. Із нерівностей

0xx



та









випливає

 

0fx fx

або

 

fx fx

при



. Але це означає, що



зростаюча функція в



,ab

Друге твердження достатньої ознаки доводиться аналогічно.



Означення 8. Зростаюча або спадна функція називається мо

нотонною

. Проміжки, в яких задана функція зростає або спадає, на&

зивають проміжками монотонності цієї функції.

Для знаходження інтервалів монотонності заданої функції



fx

доцільно дотримуватись такого порядку дій:

знайти похідну





;

знайти корені рівняння



0fx





;

242

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

3) визначити знак похідної





в кожному із інтервалів, на які

поділяється

область існування функції



fx знайденими коренями

рівняння



0fx





;

за одержаними знаками похідної зробити висновок, в якому

інтервалі

функція зростає, а в якому спадає.



Приклад 10. Витрати виробництва визначені функцією



267Vx x x

Знайти її інтервали монотонності.



Розв’язання. Задана функція існує при



,x 

, але має

економічний

зміст лише для



Знаходимо похідну:



666 1Vx x x



 

Із



610 1xx









Ці значення поділяють вісь Ох на інтервали



,1 



1,1



1, 

. В кожному з цих інтервалів





має постійний знак.

При



,1x 



0Vx





При



1,1x 



0Vx





При



1,x 



0Vx





Отже, функція



зростає при



,1 1,x  

і спадає в

інтервалі



1, 1

. З економічної точки зору, ця функція спадає в інтер!

валі



0,1

і зростає в



1, 

243

Частина 8. Диференціальне числення функцій однієї змінної



Означення 9. Функція



має при



максимум

(мінімум), якщо існує такий окіл точки

, для усіх точок

якого

виконується

нерівність

 

fx fx

для максимуму,

 

fx fx

для мінімуму.

Узагальненим терміном понять максимуму та мінімуму є екст

ремум.

Значення

аргументу



(тобто точки

) при якому функ!

ція



має екстремум (максимум або мінімум) називають точ

кою екстремуму функції

(максимуму або мінімуму, відповідно).

В економічних дисциплінах екстремум функції називають її ло

кальним оптимумом

, а процес знаходження екстремального значен!

ня функції називають оптимізацією.

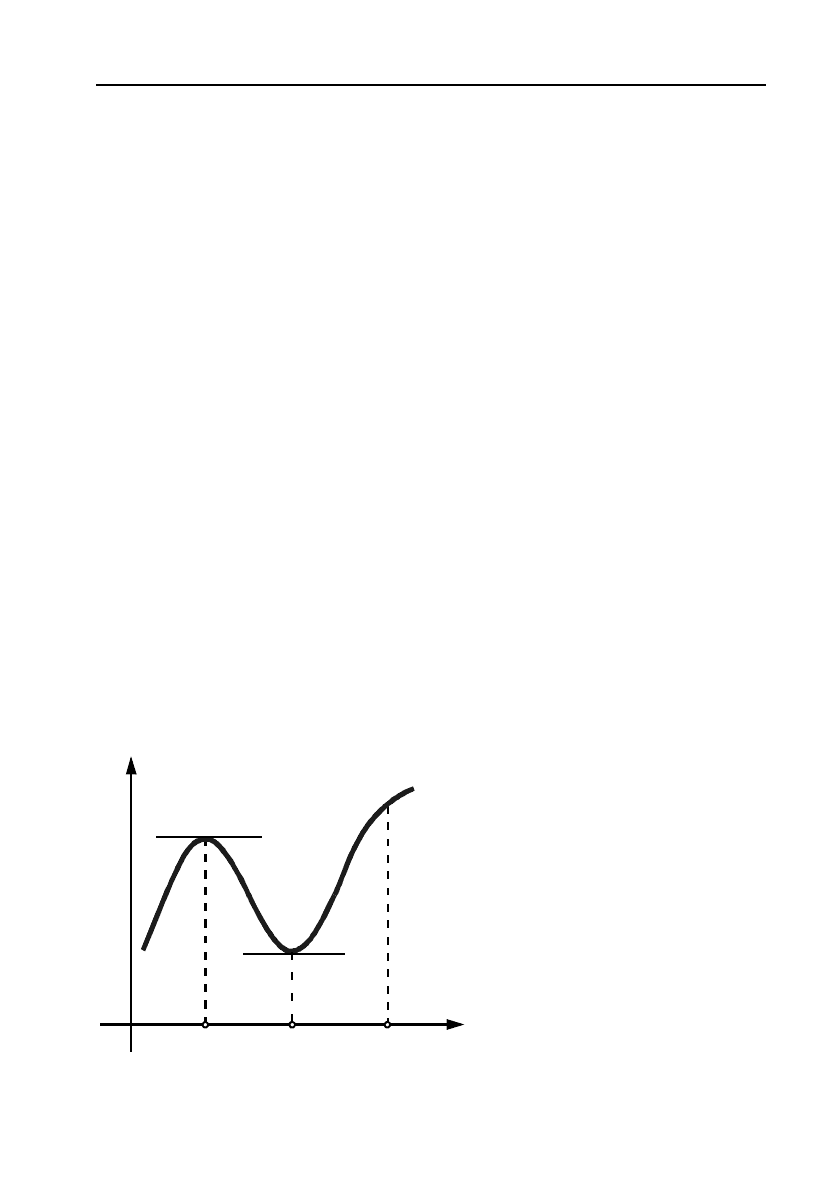
Функція, графік якої зображено на малюнку 4, має в точці

максимум, а в точці

– мінімум. В означенні 9 окіл точки

може

бути

малим, тому екстремум має локальний характер, він не зале!

жить від поведінки функції в точках, що віддалені від екстремальної

точки

. Так, на малюнку 4:

 

31max

fx fx y

В точках екстремуму дифе!

ренційованої функції дотична

до

графіка функції паралельна

осі

Ох, тому її кутовий ко!

ефіцієнт дорівнює нулю.

Рівність



0fx





(24)

називають необхідною умо

вою існування екстремуму

функції



x

, а розв’яз!

ки цього рівняння називають

y = f(x)

Мал. 4.

244

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

підозрілими на екстремум точками. Критичними точками першого

роду

називають корені рівняння (24) та точки, в яких





не існує.

Щоб визначити, в яких з критичних точок функція має екстре!

мум, треба застосувати достатні умови існування екстремуму, які опи!

сує слідуюча теорема.



Теорема (достатні умови існування екстремуму функції).

Якщо



диференційована в околі критичної точки першого

роду



і її похідна





зліва від цієї точки (при



) додатна, а справа (при



) від’мна, то в точці

функція має максимум;

2) зліва (при



) від’ємна, а справа (при



) додат

на, то в точці

функція має мінімум;

3) зліва та справа від точки

має однаковий знак, то в

точці

функція не має екстремуму.

Доведення

. Нехай при переході аргументу

через точку

зліва

направо

похідна





змінює знак з плюса на мінус. Це означає,

що зліва від

знаходиться проміжок зростання функції, а справа –

проміжок спадання функції. Тому, точка

є точкою максимуму

функції

. Аналогічно впевнюються, що при зміні знака похідної з міну!

са на плюс при переході

через

зліва направо, точка

буде

точкою

мінімуму функції



. Якщо похідна не змінює свого зна!

ка при переході

через

, то це означає, що функція



з обох

сторін точки

зростає або спадає і тому в точці

функція не має

екстремуму

. При доведенні використали існування похідної зліва та

справа

від точки

, а в точці

похідна може не існувати.

245

Частина 8. Диференціальне числення функцій однієї змінної

У зв’язку з тим, що екстремум функції – локальний оптимум дуже

часто

використовується в економічній практиці, дамо схему дослід!

ження функції на екстремум:

знаходять похідну





заданої функції;

знаходять критичні точки першого роду (значення

, при яких





не існує або дорівнює

);

визначають знак





в околі кожної критичної точки;

роблять висновок, чи має функція екстремум у знайдених точ!

ках і який саме (мінімум чи максимум);

обчислюють екстремальні значення функції в точках екстре!

муму.

Доцільно у ході дослідження використовувати таблицю по ана!

логії з наведеним нижче прикладом.



Приклад 11. Знайти екстремуми функції

29127yx x x



Розв’зання. Розв’зання проведемо згідно вказаної схеми.

знаходимо похідну:

 

6181261 2yx x x x



 

;

знаходимо критичні точки першого роду:

із

 

61 20 1, 2xx x x





інших точок не має тому, що



визначена при усіх



,x 

;

критичні точки

та

поділяють область існування функції

на

інтервали постійного знака похідної (записуємо критичні точки

та

відповідні інтервали у перший рядок таблиці 1). Визначаємо знак





в кожному інтервалі (записуємо ці знаки у другий рядок таб!

лиці 1);

згідно з достатніми умовами існування екстремуму функції

робимо

висновок відносно кожної критичної точки. (Характер пове!

дінки функції відображаємо у третьому рядку таблиці 1);

Обчислимо максимальне та мінімальне значення функції:

246

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



max

12191121712yy     



min

22894122711yy   .



,1 

1x 



1, 2

2x 



2,















max



min



8.5.2. Найбільше та найменше значення функції на відрізку

Функція, неперервна на відрізку





,ab

, досягає на цьому відрізку

свого

найбільшого та найменшого значень. Ці значення вона може

досягнути

на одному з кінців відрізку або всередині відрізку.

Тому для знаходження найбільшого та найменшого значень

функції



x

на





,ab

треба:

знайти всі критичні точки першого роду;

визначити значення функції на кінцях відрізка, тобто обчис!

лити



та



, та в тих критичних точках, що належать

відрізку

;

із одержаних значень функції обрати найбільше та найменше

значення

функції на відрізку.

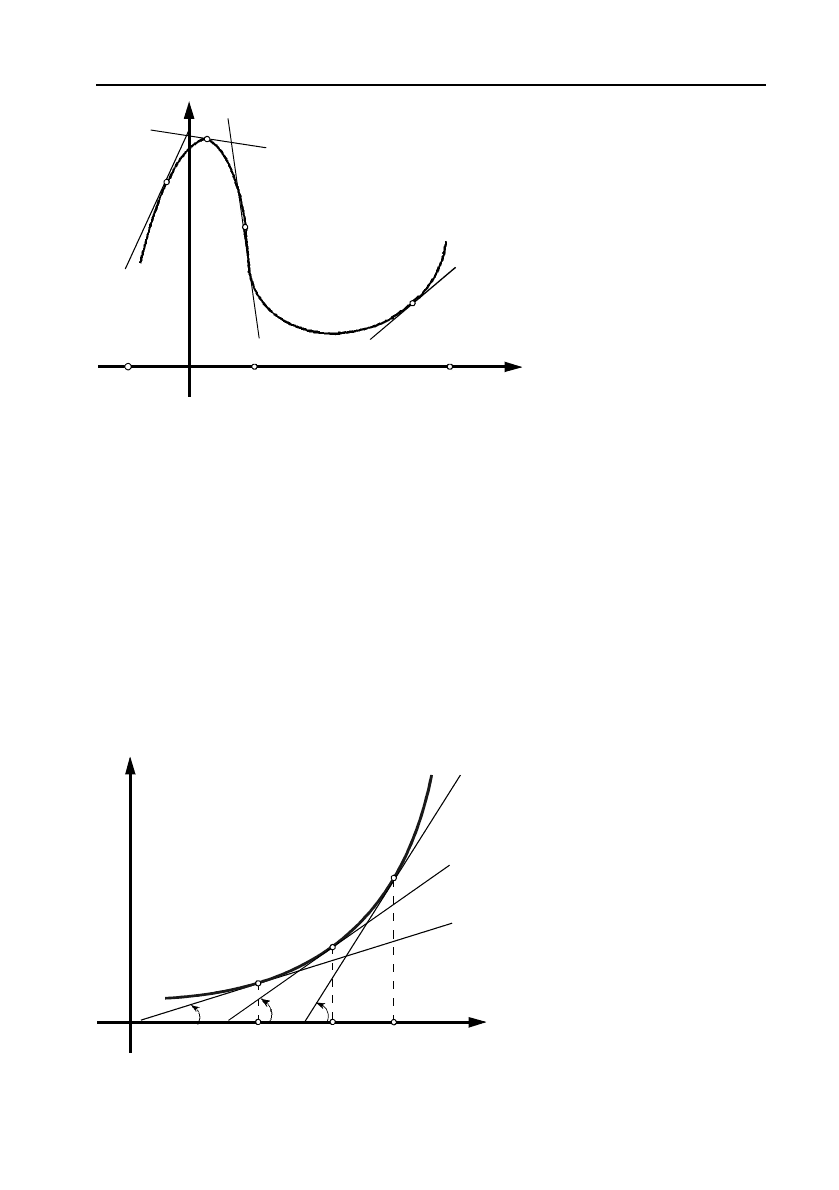
8.5.3. Опуклість та угнутість графіка. Точки перегину



Означення 10. Криву



x

називають опуклою на інтер

валі



,ab

, якщо усі точки графіка функції лежать нижче її дотич&

них на цьому інтервалі.

Криву



x

називають угнутою на



,ab

, якщо усі точки

графіка

функції лежить вище її дотичних на цьому інтервалі.

Таблиця 1

247

Частина 8. Диференціальне числення функцій однієї змінної

Функція, зображе!

на на малюнку 5, на

інтервалі



,ab

опукла,

а на інтервалі



,bc

уг!

нута.



Означення 11.

Якщо

в досить малому

околі

точки дотику

крива зліва цієї точки

лежить

по один бік до&

тичної, а справа – з іншого боку дотичної, то точку



x

нази&

вають точкою перегину кривої.

Тепер розглянемо ознаки опуклості та угнутості кривої.



Теорема. Якщо в усіх точках інтервалу



,ab



0fx





то

крива



x

є угнутою на цьому інтервалі; якщо



0fx





на

деякому інтервалі, то крива



x

опукла на цьому інтервалі.

Замість

строгого до!

ведення теореми обме!

жимось геометричним

поясненням

. Розглянемо

функцію



x

, графік

якої

угнутий (дивись на!

приклад, мал. 6).

Візьмемо декілька то!

чок

, ... кри!

вої, розташованих в по!

рядку зростання їх абсцис

123

...xxx



y = f(x)

Мал. 5.

Мал. 6.



248

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Кут нахилу дотичних до кривої в обраних точках також зростає,

тобто

123

...





. Тому

123

tg tg tg ...





Але тангенс кута нахилу дотичної до графіка функції в деякій

точці

дорівнює значенню похідної в цій точці, тому

  

123

...fx fx fx





, при

123

...xxx



Отже, похідна





– зростаюча функція, а тому її похідна до!

датна, тобто



0fx









або



0fx





Таким же чином можна пояснити ознаку опуклості. Згідно з оз!

начення 11 зліва та справа від точки перегину крива змінює опуклість

на

угнутість або угнутість на опуклість, тому друга похідна





по різні сторони від точки перегину буде мати різні знаки, а в самій

точці

перегину дорівнює нулю або не існує. Звідси випливає сліду!

юче правило для знаходження точок перегину.

Правило. Точка



буде точкою перегину кривої



fx

, якщо:



0fx





або





не існує;

знаки





зліва



x

та справа



x

різні.

Якщо





не змінює свій знак при переході аргументу через

, то при



перегину не буде.

Рівність умови 1 цього правила називають необхідною умовою, а

умову

2 – достатньою умовою існування точок перегину графіка функції.



Означення 12. Значення

, при яких



0fx





або не існує,

називають критичними точками другого роду функції





Приклад 12. Знайти інтервали опуклості, угнутості та точки

перегину

функції





(крива Гауса).

249

Частина 8. Диференціальне числення функцій однієї змінної

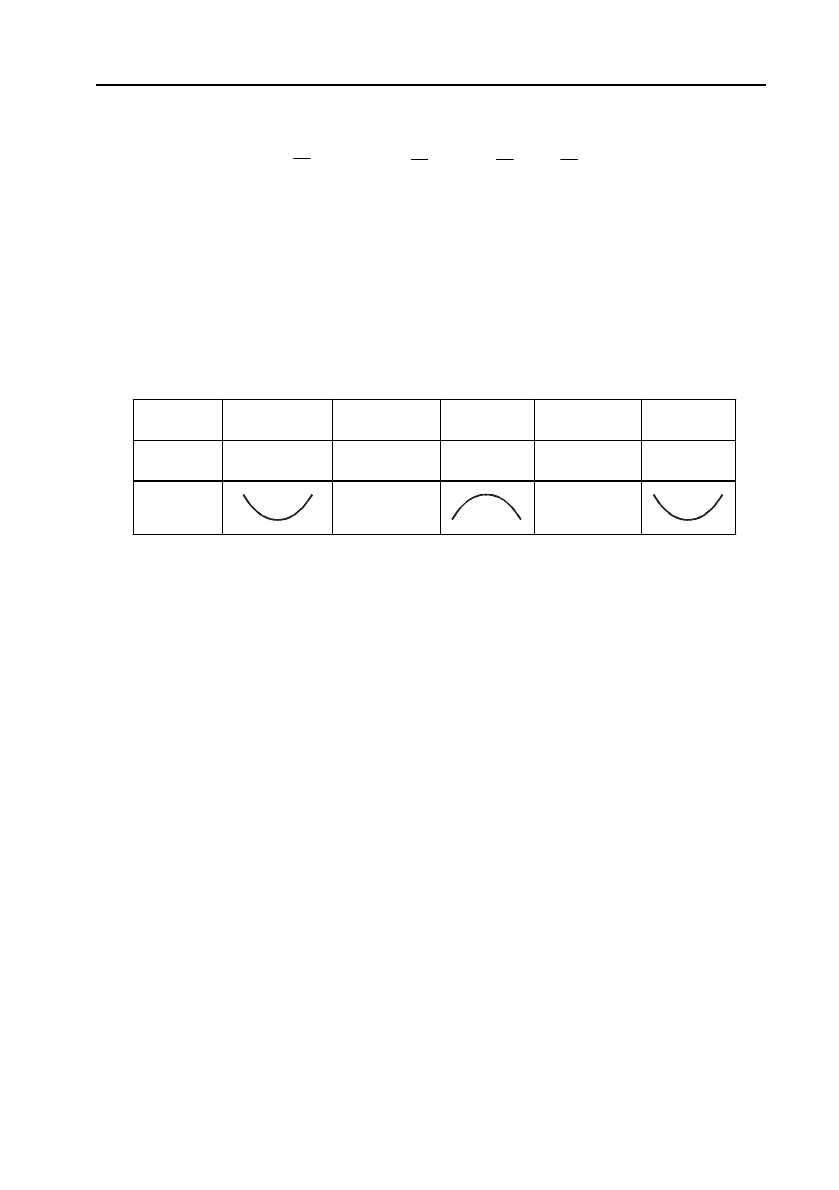
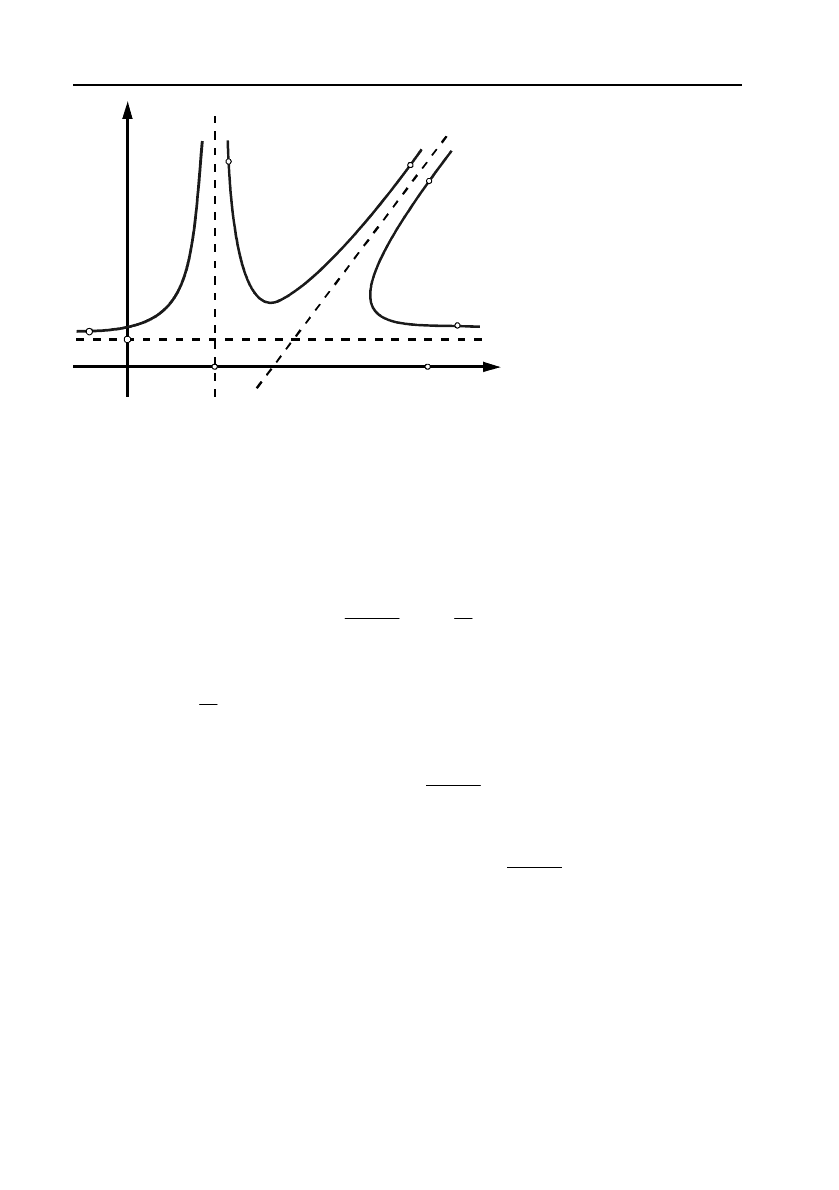
8.5.4. Асимптоти кривої



Означення 13. Пряму лінію називають асимптотою кривої



fx

, якщо відстань точки М кривої від цієї прямої прямує до

нуля

при віддалені точки М в нескінченність.

Асимптоти можуть бути вертикальними, похилими, та горизон!

тальними (мал. 7).

Вертикальні асимптоти існують, коли функція має розриви дру!

гого роду. Якщо

точка такого розриву, то



буде рівнянням

вертикальної

асимптоти.

Рівняння похилої асимптоти будемо шукати у вигляді рівняння

прямої

з кутовим коефіцієнтом, тобто у вигляді

kx b

. Відстань



Розв’язання. Знайдемо другу похідну цієї функції. Маємо:









222

xxx

ye xe ex





   

Друга похідна визначена для усіх

. Тому критичні точки друго!

го роду знайдемо із рівності









Визначимо знак другої похідної при проходженні

через кожну

критичну

точку. За результатами цього дослідження складемо таб!

лицю 2.

Таблиця 2

Отже

, обидві точки



та



є точками перегину;



1, 1



–

інтервал опуклості;



 





– інтервали угнутості графіка.

Значення функції в точках перегину буде



1/2

пер

yf e







,1 

1x 



1,1

1x 



1, 













точка

перегину

точка

перегину

250

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

точки



, що

належить

кривій



fx

, до прямої

kx b

можна на!

ближено виразити че!

рез різницю між орди!

натами кривої та

прямої

при однаково!

му значенні

 

dfx kxb

За означенням асимптоти

0d 

при

x 

, тобто



lim 0

fx kx b









Якщо цю рівність поділити на

, то одержимо:



lim 0





 





Але

lim 0





, тому



lim





. (25)

Якщо не існує скінченого значення



lim



, то похилої асим!

птоти не існує. Якщо вказана границя існує, то за формулою (25)

знаходимо

, а за формулою



lim

bfxkx













(26)

знаходимо

і таким чином одержимо рівняння похилої асимптоти

вигляду

kx b



Мал. 7.

y = b

x = a