Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


211
Частина 7. Вступ до математичного аналізу
D(x) = D(3200) – D(3100) = (1003200 – 0,013200] –
–[1003200 – 0,013100] = 217600 – 213900 = 3700.
Позначимо прибуток Р(х). Тоді
P(x) = D(x) – V(x) = 100х – 0,01х
2
– (20000 +40х) =
=60
х – 0,01х
2
– 20000.
Приріст прибутку буде
Р(х) = Р(3200) – Р(3100) = [60
3200 – 0,013200
2
– 20000] –
–[603100 – 0,013100
2
– 20000] = 69600 – 69900 = –300.
Отже, прибуток зменшиться на 300 гривень.
Середня величина приросту прибутку на одиницю приросту про!
дукції буде
300
3
100
Px
x
.
Отже, кожна одиниця додаткової продукції зменшує прибуток на
3 гривні.
Приклад 5. (Зміна кількості населення). Зміна кількості
населення
деякого міста за час t, що вимірюється роками, здійснюєть!
ся за формулою
P(t) = 10000 + 1000t – 120t
2
.
Визначити середню швидкість зростання населення в період між
часом
: a) t = 3 та t = 5; b) t = 3 та t =
1
3
2
.
Розв’язання. Середню швидкість зростання населення міста за
час
t знайдемо за формулою
P
tPttPt
tt
.
a) В цьому випадку:
t = 5 – 3 = 2
P(t) = Р(5) – Р(3) = [10000 + 5000 – 120
25] –
–[10000 + 3000 – 1209] = 2000 – 1920 = 80.
Середня швидкість зростання населення міста в цей період буде
80:2 = 40.
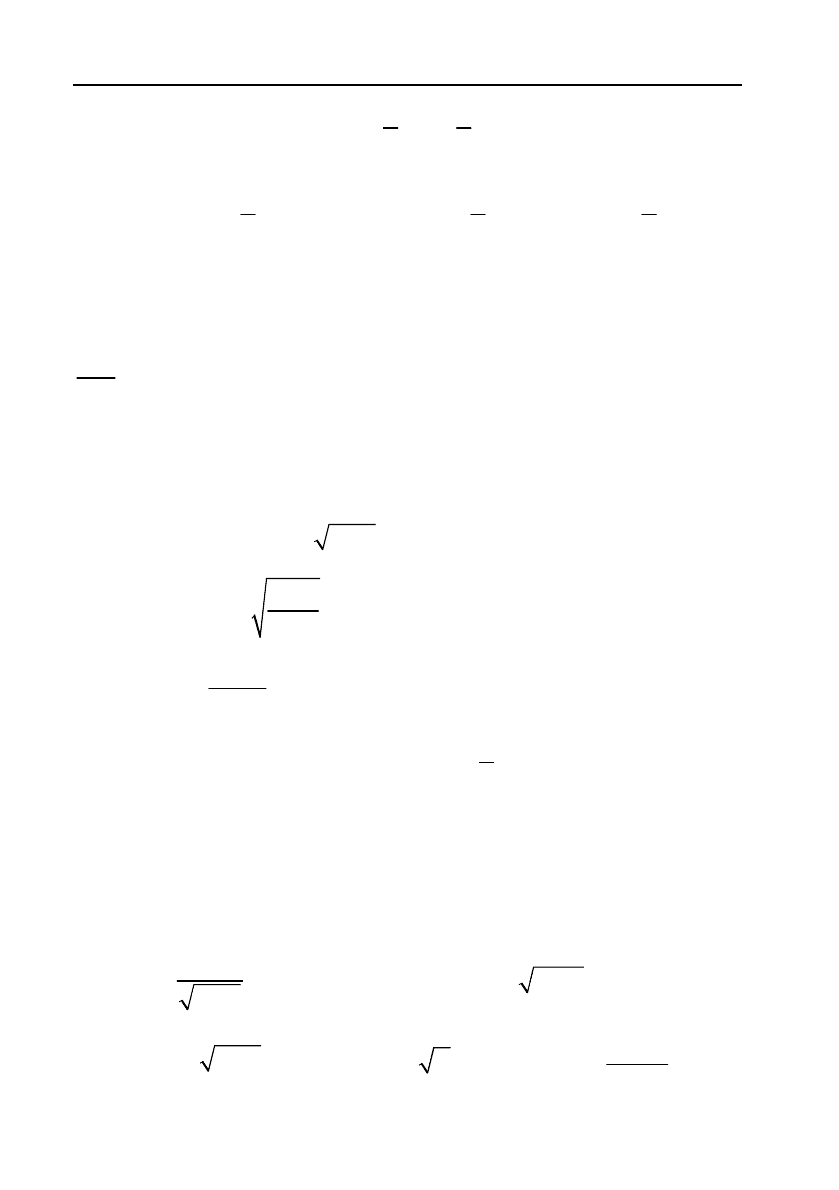
212
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
b) В цьому випадку:
11
33
22
t
.
2
111
3 3 10000 3 1000 120 3
222
Pt P P
10000 3000 120 9 500 390 110
.
Отже, середня швидкість зростання населення міста в цей час буде
110
220.
1
7.6. Вправи
1.
Знайти значення функції в заданих точках.
а) F(x, у) = х
3
– 3ху – у
2
+ 2х + у при х = 4, у = 3;
b)
2cos4 1fx x x
при х = 0;
c)
2
2ln
x
fx
x
при x = 1;
d)
2
23
1
t
t
t
при t = 1;
e)
у = 8х – 2х
2
при х = 1 та при х =
1
2
.
2.
Задану функцію записати у вигляді ланцюга рівностей, кожна
ланка
якого містить основну елементарну функцію:
а)
arcsin 3 ;
x
y
b)
lgsin3
y
x
; c)
2
5
6
3cos ln2 .
x
yx
3.
Знайти область існування функції:
a)
1
;
1
y
x
b)
3cos2 2;
fx x x
c)
ln 1 ;
y
x
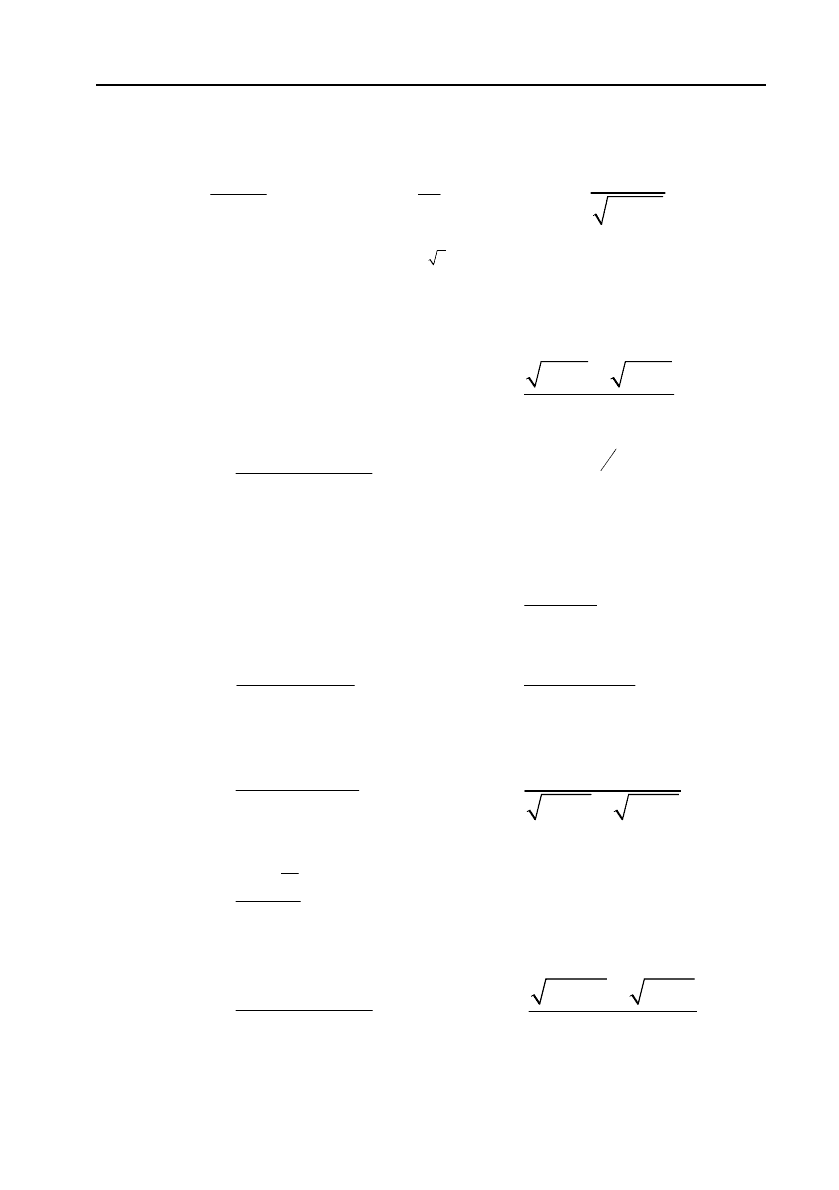
d)
sin 3yx
; e)
2
2
1
4
x
y
x
.
213
Частина 7. Вступ до математичного аналізу
4. Довести, що задана змінна є нескінченно малою або нескінчен!
но великою:
a)
2
;
1
n
n
n
b)
1
;
!
n
n
c)
2
1
;
1
n
n
d)
2
1;
n
n
n
e)
2.
n
n
5. Знайти вказані границі:
a)
1)
2
2
lim 3 7 1 ;
x
xx
2)
11
lim ;
4
x
x
x
x
3)
2
42
341
lim ;
23
x
xx
x
xx
4)
1
0
lim 1 2 ;
x
x
x
b)
1)
2
1
lim 2 3 1 ;
x
xx
2)
2
4
16
lim ;
4
x
x
x
3)
43
2
21
lim ;
42
x
xx
x
x
4)
3
tg sin
lim ;
x
xx
x
c)
1)
3
3
272
lim ;
643
x
xx
xx
2)
2
3
12
lim ;
24
x
xx
xx
3)
2
0
sin
4
lim ;
2
x
x
x
4)
lim 2 3 ln 2 ln ;
x
x
xx
d)
1)
4
24
14
lim ;
32
x
xx
x
xx
2)
2
4
12 4
lim ;
28
x
xx
xx
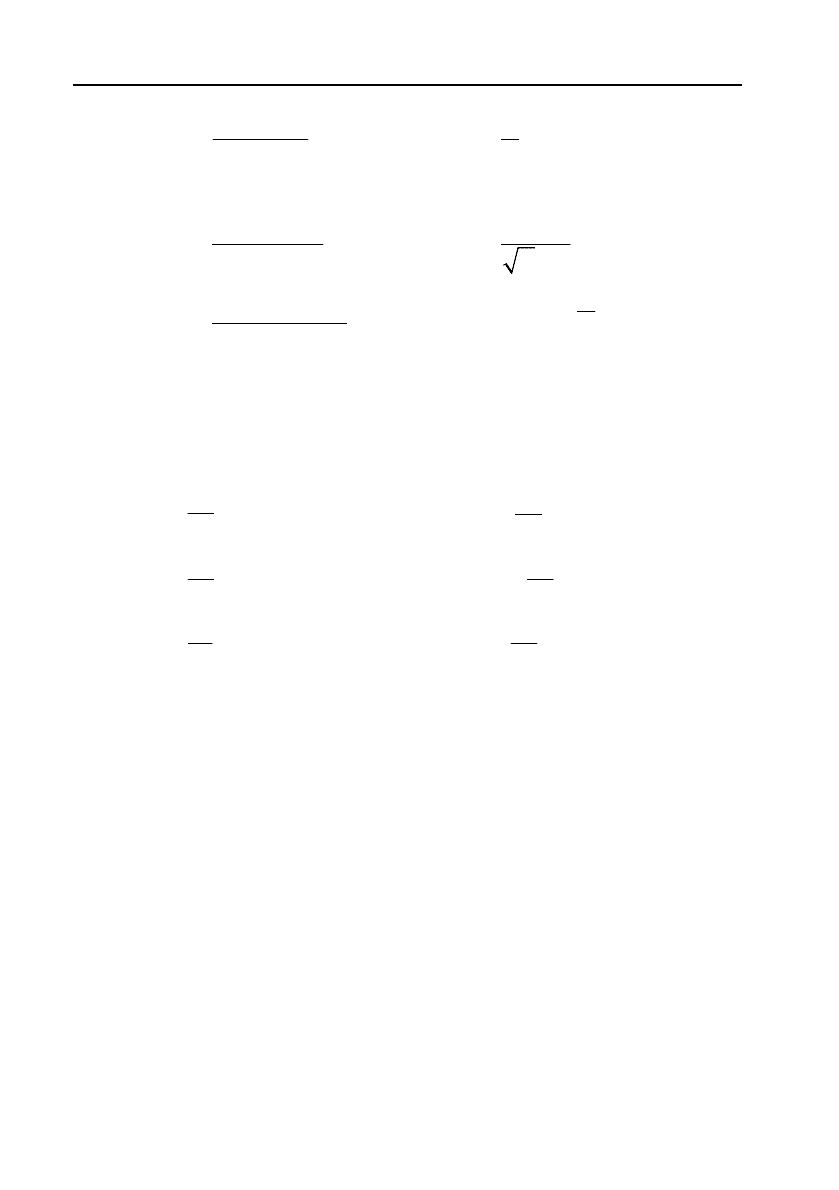
214
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
3)
2
0
1cos3
lim ;
x
x
x
4)
lim ln 3 4 ln3 ;
4
x
x
x
x
e)
1)
2
2
1
2
lim ;
32
x
xx
xx
2)
9
9
lim ;
3
x
x
x
3)
3
0
cos cos
lim ;
sin2
x
x
x
x
x
4)
10
2
0
lim 2 1 .
x
x
x
6.
Задана функція
yf
x
та два значення аргументу
1
x
та
2
x
.
Треба: 1) встановити, чи буде функція неперервною в кожній точці;
2)
у випадку розриву функції знайти її однобічні границі зліва та
справа
; 3) зробити схематичний малюнок.
а)
1
4
12
5, 2, 4;
x
yxx
b)
1
3
12
6, 4, 3;
x
yxx
с)
1
5
12
7, 7, 5;
x
yxx
d)
1
9
12
10 , 8, 9;
x
yxx
e)
1
1
12
4, 3, 1;
x
yxx
f)
1
2
12
8, 4, 2.
x
yxx
7.
Задачі економічного змісту.
а) мале підприємство встановило, що витрати на виготовлення х
окремих
виробів задовольняють такій закономірності
V(x) = 0,001x
3
– 0,3x
2
+ 40x + 1000.
Знайти: приріст витрат, коли кількість виробів зросте з 50 до 100
та середні витрати на виготовлення кожної одиниці виробу, коли їх
кількість
зросте з 50 до 60.
b)
загальний щотижневий доход D в гривнях, одержаний
підприємством
після продажу виготовлених х одиниць виробів, має
таку
закономірність
2
500 2 .
D
xxx
Визначити середнє значення доходу на одиницю приросту виго!
товленої продукції, якщо її кількість х зросте з 100 до 120.

215
Частина 7. Вступ до математичного аналізу
7.7. Завдання для індивідуальної самостійної роботи
1.
Знайти область визначення функції:
а)
2
1;
y
xNxN
b)
2
1
log 1 .
N
y
xNxN
2. Знайти границі:
a)
22
3
lim ;
xN
x
xN
x
N
b)
2
1
1
lim .
1
xN
xN
xN
3. Дослідити неперервність функції та побудувати її графік:
a)
1
,1;
,1;
N
xx
y
xx
b)
2
31,1;
,1.
xxx
y
xNx x

216
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Частина 8
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ
8.1. Похідна і диференціал
8.1.1. Деякі задачі, що привели до поняття похідної
а) Задача про швидкість прямолінійного руху
Нехай
тіло рухається прямолінійно вздовж осі
0
s
, але нерівномір!
но. Тоді координата
s
точки буде змінюватись з часом за деяким
законом
, тобто
()
sst
. Починаючи з деякого моменту
t
, за час
t
тіло пройде шлях
()()
s
st t st
.
Середня швидкість
c
v
руху за проміжок
t
буде
c
s
v
t
. Серед!
ня швидкість дає лише наближене уявлення про рух в окремі мо!
менти часу. Так, на початку проміжку
t
тіло могло рухатись при!
скорено, а в кінці цього проміжку часу – уповільнено.
Коли проміжок часу
t
зменшується, тоді
c
v
наближається до
швидкості
руху в момент
t
, що відповідає початку проміжку
t
.
Означення 1. Миттєвою швидкістю
v
(або швидкістю в
момент
t
) називають границю відношення приросту шляху
s
до
приросту
часу
t
, коли
0t
, тобто
t
s
vt
t
0
() lim
, (1)
Миттєва швидкість
v
залежить від часу
t
, а також від вигляду
функції
()
sst
.
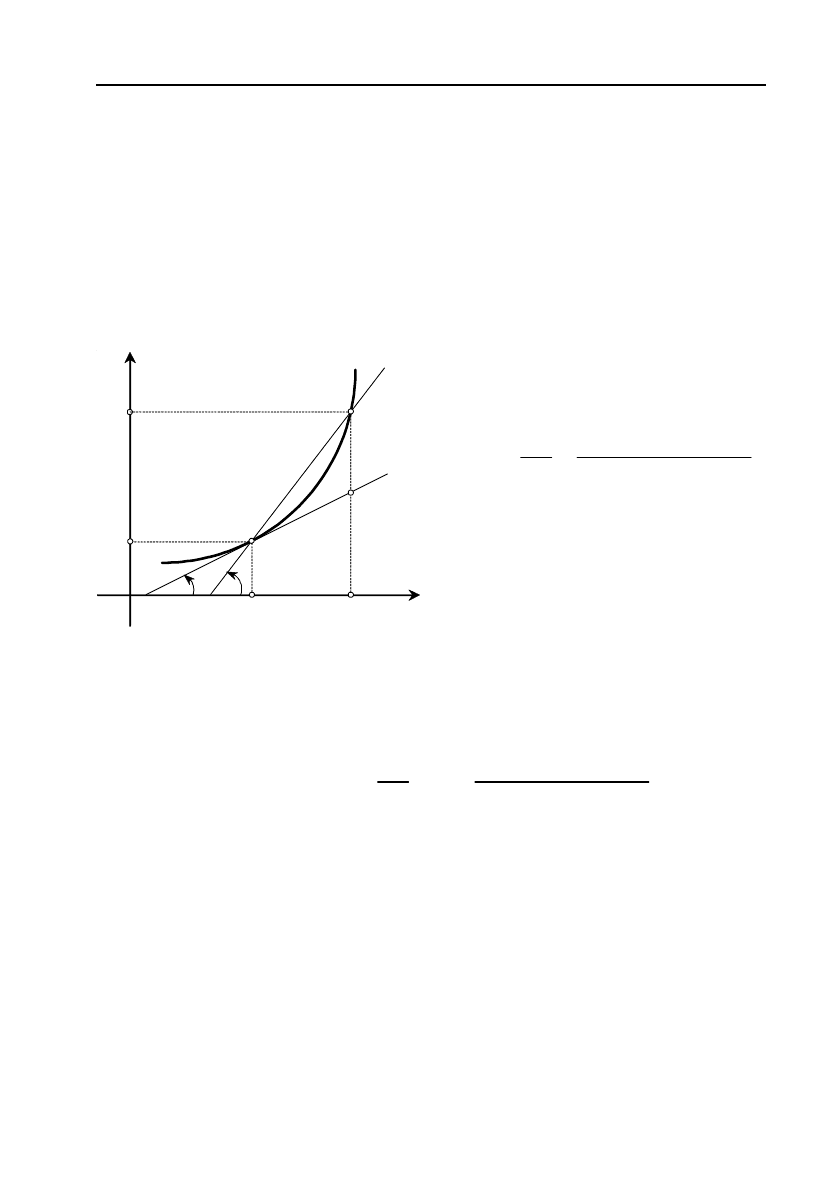
217
Частина 8. Диференціальне числення функцій однієї змінної
b) Задача про дотичну
Нехай
задана функція
()
yf
x
. Графіком цієї функції на пло!
щині
xO
y
буде деяка крива лінія.
Означення 2. Дотичною до кривої
()
yf
x
в точці М
(
,
)
xy
(точка дотику) називають граничне положення МТ січної ММ
1
, коли
точка М
1
, рухаючись вздовж кривої, прямує до точки дотику М (див.
мал. 1).
З малюнка видно, що тангенс
кута
нахилу січної ММ
1
до осі
Ox
буде
y
fx x fx
xx
1
()()
tg
.
Із означення дотичної випли!
ває, що її кутовий коефіцієнт
k tg
є границя, до якої пря!
мує кутовий коефіцієнт
k
11
tg
січної при необмеженому набли!
женні точки М
1
до точки М, тоб!
то при
0x
.
Отже, одержали
xx
yf
xx
f
x
k
x
x
00
()()
tg lim lim
. (2)
с) Задачі про маргінальні вартість, доход, прибуток
Маргінальними витратами називають
гранично можливі витра!
ти в умовах хоча б постійного відтворення виробництва відповідної
продукції
. Аналогічно визначають маргінальні доходи та прибуток.
Позначимо через
()
Vx
,
()
D
x
та
()
Px
витрати, доходи та при!
буток виробництва х одиниць продукції. Кожна з цих величин є
певною
функцією кількості одиниць х виробленої та проданої про!
дукції.
0
Y
X
y
x
M
M
1
T
y
y
xx
1
Мал. 1.

218
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Якщо підприємство збільшує випуск продукції на
x
одиниць,
то ці функції одержать приріст
() ( ) ()
Vx Vx x Vx
;
() ( ) ()
D
xDxxDx
;
() ( ) ()
P
xPxxPx
.
Відношення приросту функцій до
x
характеризує приріст відпо!
відної функції на одиницю приросту продукт, а границя цього відно!
шення при
0x
стає маргінальною.
Отже, маємо:
Маргінальна вартість
00
() ( ) ()
lim lim
xx
Vx Vx x Vx
xx
. (3)
Маргінальний доход
00
() ( ) ()
lim lim
xx
D
xDxxDx
xx
. (4)
Маргінальний прибуток
00
() ( ) ()
lim lim
xx
P
xPxxPx
x
x
. (5)
Розглядаючи різні задачі, ми одержимо однакові формули (1)–
(5)
для їх розв’язків, а саме, шукану величину знаходять шляхом
застосування
граничного переходу до відношення приросту функції
до
приросту аргументу, коли приріст аргументу прямує до нуля.
8.1.2. Означення похідної та деякі її інтерпретації
Означання 3. Похідною функції
()
yf
x
за аргументом
x
називають границю відношення приросту функції
y
до приросту
аргументу
x
, коли
x
довільним образом прямує до нуля. Якщо ця
границя
існує, то її позначають через
()
f
x
або
y
або
dy
dx
, або

219
Частина 8. Диференціальне числення функцій однієї змінної
()df x
dx
. Отже, математично похідна функції визначається за фор&
мулою:
0
()()
( ) lim
x
f
xx
f
xx
fx
x
. (6)
Відмітимо, що похідну
()
f
x
одержали за допомогою гранично!
го переходу при постійному
x
, тому при
x
a
вона приймає кон!
кретне значення, яке позначають
()
f
a
або
x
a
dy
dx
.
Означання 4. Операцію знаходження похідної функції
()
y
fx
називають диференціюванням цієї функції. Функцію
()
f
x
,
яка має похідну в точці х, називають диференційованою в точці х.
Якщо функція має похідну в кожній точці деякого проміжку, то її
називають
диференційованою у цьому проміжку.
Повертаючись до розглянутих вище задач, які привели до понят!
тя похідної, робимо такі висновки:
1) механічний зміст похідної: похідна
()
St
є величиною миттє!
вої швидкості в момент
t
тіла, що рухається за законом
()
SSt
;
2) геометричний зміст похідної: похідна
()
f
x
дорівнює куто!
вому коефіцієнту дотичної до графіка функції
()
y
fx
в точці з
абсцисою
x
;
3) економічний зміст похідної: похідні
()
Vx
,
()
D
x
,
()
P
x
до!
рівнюють маргінальній вартості, доходу та прибутку, відповідно.
Нижче, у розділі 8.6, буде детально розглянуто ще один при!
клад економічного змісту похідної першого порядку, а саме елас!
тичність функції, яку часто застосовують при розв’язанні економіч!
них задач.

220
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
8.1.3. Зв’язок між неперервністю та диференційованістю
функції
Теорема. Якщо функція y = f(x) диференційована в деякій
точці
0
x
, то вона в цій точці неперервна.
Доведення
. Якщо
()
y
fx
диференційована в точці
0
x
, то згідно
з
означенням похідної при
0
x
x
існує скінченна границя
0
0
lim ( )
x
y
fx
x
.
В силу того, що границя змінної величини відрізняється від самої
змінної
лише на нескінченно малу
, то з останньої рівності маємо
00
() ()
y
fx y fx x x
x
. (7)
Оскільки
0
()
f
x
–
постійна величина, то з властивостей не!
скінченно малих випливає, що обидва доданки в правій частині (7)
є нескінченно малих величинами. Їз (7) випливає, що
0
y
, тоб!
то функція
()
y
fx
неперервна в точці
0
x
. Теорема доведена.
Наслідок. З цієї теореми випливає, що неперервність функції є
необхідною умовою диференційованості функції. Це означає, що в точ&
ках розриву функція не має похідних, тобто вона не диференційована.
Функція, яка неперервна в точці
0
x
, може бути не диференційо!
ваною в цій точці. Наприклад, функція
y
x
неперервна в точці
0x
, але не має похідної в цій точці тому, що
0
lim 1
x
y
x
, а
0
lim 1
x
y
x
,
тобто границя відношення
y
x
залежить від способу прямуван!
ня
0x
.
