Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

181

Частина 6. Векторна алгебра та аналітична геометрія

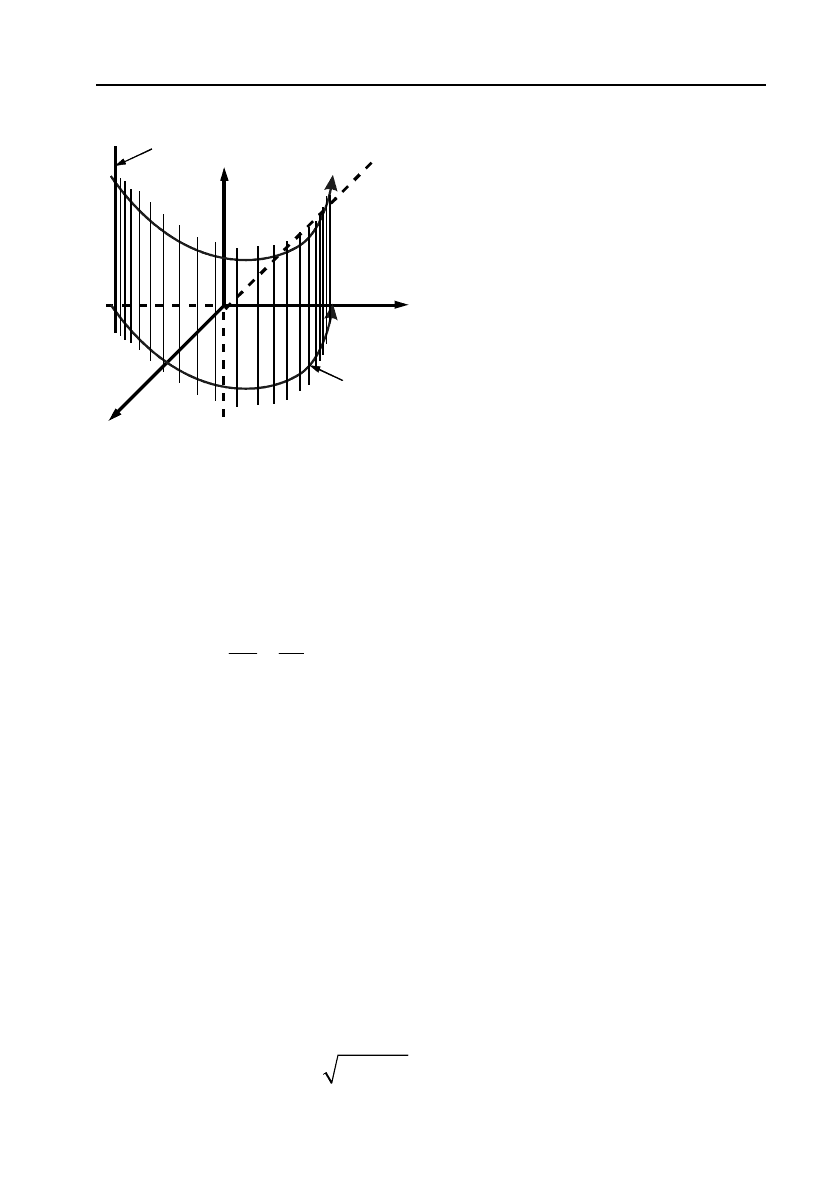
Приклад циліндричної поверхні зображено на мал. 18.

Якщо твірна циліндричної по!

верхні паралельна осі Oz, а напрям!

на l лежить в площині хOу і зада!

на рівняннями



Fxy















, (52)

тоді рівнянням циліндричної по!

верхні буде



;

Fxy















. (53)

Рівняння F(x, z)= 0 визначає циліндричну поверхню з твірною,

що паралельна Oу, при F(y, z) = 0 твірна паралельна осі Oх.

Наприклад, рівняння

431xy

визначає еліптичний циліндр,

твірна якого паралельна Oz.

Рівняння

 визначає гіперболічний циліндр, твірна яко!

го паралельна Oу.

Рівняння у

= 8z визначає в просторі параболічний циліндр, твірна

якого

паралельна осі Oх.

b) Поверхні обертання

Правило. Для

одержання рівняння поверхні обертання навколо

однієї

з координатних осей треба:

в рівнянні лінії обертання залишити незмінною координату,

однойменну з віссю обертання;

другу координату рівняння лінії обертання замінити на плюс&мінус

квадратний

корінь із суми квадратів двох інших просторових координат.

Наприклад, нехай обертається пряма z = ky навколо осі Oу. Згідно

правилом в рівнянні z = ky залишимо незмінною координату у, а

замість

z підставимо

xz

Мал. 18.

182

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

6.2.9. Вправи до розділу 6.2

1. Визначити, які з точок М

(3, 1), М

(2, 3), М

(6, 3), М

(–3, 3),

(3, –1), М

(–2, 1) належать прямій 2х – 3у – 3 = 0 і які не нале!

жать їй.

Скласти рівняння прямої, що проходить через точку M

(–1, 3):

паралельно прямій х – 5у + 2 = 0;

перпендикулярно до прямої 3х – у + 4 = 0.

Знайти точки перетину прямої 2х – 3у – 12 = 0 з осями коор!

динат, записати рівняння цієї прямої у відрізках та побудувати її.

Скласти рівняння прямих, що проходять через точку М

(2,–3):

паралельно осі Oх;

паралельно осі Oу;

перпендикулярно до прямої х – 3у – 7 = 0.

Довести, що пряма 2х – 3у + 2 = 0 паралельна прямим:

а) 6х – 9у + 5 = 0; b)

x

; с)

xy



;

та перпендикулярна прямим:

а) 3х + 2у – 5 = 0; b)





; с)

xy





Таким чином, одержимо рівняння конуса:

xzky

або

2222

0xzky 

Підкреслимо, що наведене правило дозволяє одержати рівняння

багатьох

важливих поверхонь.

222

xyz





– рівняння еліпсоїда обертання навколо Oz;

222

xyz





– рівняння гіперболоїда обертання навколо Oz;

qz

– рівняння параболоїда обертання навколо Oz.

183

Частина 6. Векторна алгебра та аналітична геометрія

6. Знайти відстань між паралельними прямими:

х – 2у + 6 = 0 та 2х – 4у + 7 = 0;

b) 2

х – 3у + 2 = 0 та 6х – 9у + 5 = 0;

c) 2

х – 3у + 2 = 0 та

x

Знайти кут між прямими:

a) 5

х – у + 7 = 0 та 2х – 3у + 1 = 0;

b) 2

х + у = 0 та у = 3х – 4;

c) 3

х – 2у + 7 = 0 та 2х + 3у – 3 = 0;

х – 2у – 4 = 0 та 2х – 4у + 3 = 0;

у = –2х + 3 та у = 3х + 5.

Визначити при яких а та b прямі ах – 2у – 1 = 0 та 6х – 4у –

– b = 0:

а) мають одну спільну точку; b) паралельні; с) співпадають?

Скласти рівняння висот трикутника з вершинами А(0, –1),

В(1, –3) та С(–5, 2).

10.

Побудувати на площині область розв’язків системи лінійних

нерівностей

453

73 71

















;b)

6517

234

4917

















;

11 3 24

94110

27 15













 



;d)

98157

311 16













 



11.

Знайти точки рівноваги та області прибутку і збитків ком!

панії, що виготовляє щомісяця х виробів вартістю р гривень кожен,

а сума загальних щомісячних витрат у

має таку закономірність:

a) p = 4

= 2,8х + 600;

р = 7 у

= 1000+ 5х;

р = 10 у

= 80 – 4х + 0,1х

;

d) p = 10 y

= 2000+ 100

184

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

12. Скласти рівняння площини, що проходить через точки

(4, 6, 1), М

(1, 0, –2), М

(4, –2, 4), привести його до загального

вигляду

. Побудувати цю площину.

13.

Скласти рівняння площини, що проходить через точку

(2, 1, –1) перпендикулярно вектору



= (1, –2, 3).

14.

Побудувати площини, що задані рівняннями:

a) 2x – y – 2z + 5 = 0; b) x + 5y – z = 0;

c) 3

х – 2у – 2 = 0;d) 5y – 3z = 0; е) х + 2 = 0.

15.

Виявити паралельність пар площин:

а) 2х – 3у + 5z – 7 = 0 та 2х – 3у + 5z + 3 = 0;

b) 4

х + 2у – 4z + 5 = 0 та 2х + у + 2z – 1 = 0;

с) х – 3z + 2 = 0 та 2х – 6z – 7 = 0.

а також перпендикулярність пар площин:

a) 3

х – у – 2z = 0 та х + 9у – 3z + 2 = 0;

b) 2

х + 3у – z – 3 = 0 та х – у – z + 5 = 0;

c) 2

х – 5у + z = 0 та 3х – у – 5z + 1 = 0.

16.

Знайти координати фокуса, рівняння директриси, а також

побудувати

параболу:

а) у

= –12х; b) x

= 4у; с) х

= –5у; d) y

= 6x.

17.

Визначити координати вершин, фокусів, а також побудувати

гіперболу

а) 9х

– 16у

+ 144 = 0; b) х

– 4у

– 16 = 0; с) 4х

– 9у

– 25 = 0.

18.

Скласти рівняння параболи, вершина якої знаходиться у по!

чатку координат, якщо відомо:

парабола розташована у правій півплощині симетрично віднос!

но осі Oх і її параметр р = 3;

парабола розташована у лівій півплощині симетрично віднос!

но осі Oх і її параметр р = 0,5;

парабола розташована у верхній півплощині симетрично віднос!

но осі Oу і її параметр р =

. Побудувати ці параболи, їх фокуси та

директриси

19.

Скласти канонічне рівняння еліпса з фокусами на осі Oх, якщо:

півосі еліпса дорівнюють 5 та 2;

відстань між фокусами дорівнює 6, а більша вісь 10;

185

Частина 7. Вступ до математичного аналізу

6.2.10. Завдання для індивідуальної роботи з аналітичної

геометрії

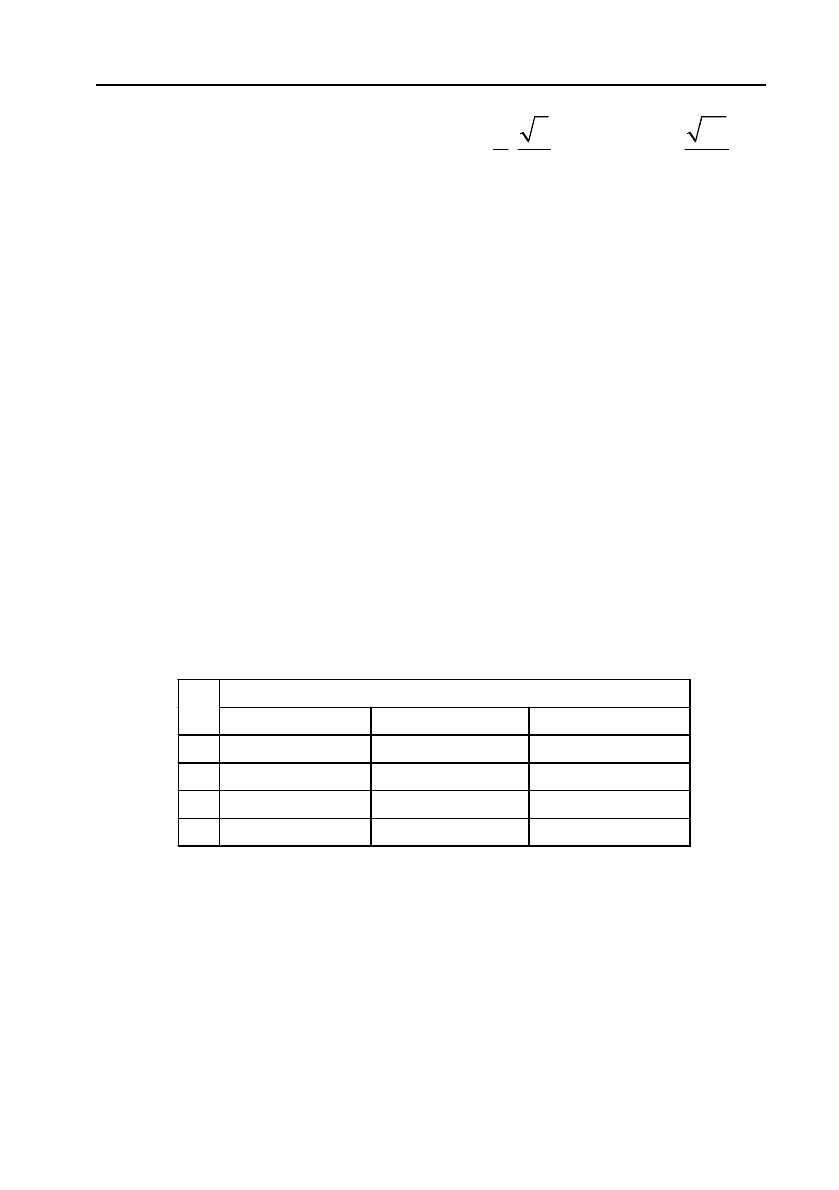
1. Використовуючи задані координати вершин трикутника ABC

побудувати трикутник та скласти чи знайти:

a) довжину сторони АС;

b) загальне рівняння АС;

c) відстань точки В від АС;

d) рівняння медіани сторони ВС у канонічній формі;

e) кут АСВ:

f) рівняння прямої, що проходить через вершину В паралельно

AC (N – номер варіанта).

2. Побудувати графіки прямих і знайти координати точок їх пе#

ретину (N – номер варіанта):

a) (N + 1)х + (N + 2)у – 2N – 3 = 0 та у = (N + 3)х – N – 2;

b) (N + 3)х – (N + 4)у + N + 5 = 0 та х = (N + 1)у – 2N – 1;

c) (N + 2)х + (N + l)y – 4N – 5 = 0 та (N + 5)х – (N + 3)у + 2N+

+4 = 0;

d) (N+ 4)х + Ny – 5N – 16 = 0 та (N +

l)y – (N + 3)х – 3N – 1 = 0.

c) еліпс проходить через точки







та









20. Побудувати у системі координат піраміду

1234

MMM

a) М

(3, 1, 4) М

(–1, 6, 1) M

(–1, 1, 6) М

(0, 4, –1);

b) М

(6, 6, 2) М

(5, 4, 7) М

(2, 4, 7) М

(7, 3, 0);

c) М

(7, 5, 3) М

(9, 4, 4) М

(4, 5, 7) М

(7, 9, 6).

Координати

А В C

1. (N; N+1) (N+2; N+6) (N+3; N+5)

2. (N+1; N) (N; N+2) (N+4; N+3)

3. (N+2; N+l) (N+3; N+2) (N+4; N)

4. (N+l; N+3) (N+2; N+4) (N+1; N)

186

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Частина 7

ВСТУП ДО МАТЕМАТИЧНОГО АНАЛІЗУ

Математичний аналіз вивчає змінні величини та функціональні

залежності

між ними. Під час досліджень широко застосовуються

метод

граничного переходу та метод координат, який дозволяє не

тільки

наглядно представляти залежності, що вивчаються, але й вста!

новлювати нові залежності.

7.1. Функції та способи їх задання

7.1.1. Характеристики змінних величин



Означення 1. Величиною називають те, що можна виразити

певних одиницях та характеризувати числовим значенням.

Наприклад, площа та довжина кола – величини тому, що вимі!

рюються в певних одиницях і характеризуються деяким числовим

значенням

. Коло не буде величиною тому, що для нього характерна

лише

певна форма.

Величини бувають розмірні та безрозмірні. Розмірністю вели

чини

називають ту одиницю, через яку величина виражається.

Наприклад, розмірність площі – см

, м

, км

Додавати та віднімати можна величини лише однакової

розмірності. Множити та ділити величини можна будьякої

розмірності.

Наприклад

, швидкість

10 .

км

год

Якщо поділити дві величини однакової розмірності, то одержимо

безрозмірну

величину. Наприклад,

см



В математиці найчастіше вивчають безрозмірні величини, які

повністю

характеризуються лише своїм числовим значенням. Вели!

чини бувають постійні та змінні.

187

Частина 7. Вступ до математичного аналізу

7.1.2. Поняття та характеристики функцій

Часто

при дослідженні певного явища доводиться мати справу

одночасно

з деякою кількістю змінних величин. Наприклад, для виго!

товлення виробів кількістю у застосовують х сировини, z палива і т.д.

Деякі з розглядаємих змінних можуть бути зв’язані одна з іншою

так

, що зміна однієї величини приводить до зміни іншої величини.

В цьому випадку кажуть, що між цими величинами існує функціо!

нальна залежність.

Серед функціонально залежних величин можна вказати такі ве!

личини, значення яких можна обирати довільно (ці величини нази!

вають незалежними змінними), тоді як значення інших величин виз!

начаються значеннями незалежних змінних (їх називають залежними

величинами

Наприклад, якщо розглядати зв’язок між величинами кормів х та

надоїв

у, тоді доцільно за незалежну змінну прийняти х, а надої





буде залежною змінною.



Означення 3. Змінна величина у називається функцією змінної

величини х, якщо вказаний закон, за яким кожному значенню х, взя&

тому з області можливих значень, відповідає певне дійсне значення у.

Змінну величину х називають незалежною змінною або аргументом.

Якщо у є функцією х, то кажуть, що величини х та у зв’язані

функціональною

залежністю і позначають





(замість літери

f можна використовувати інші літери: F, Ф, u, v,



, у).



Означення 4. Функція



fx

називається однозначною,

якщо кожному значенню х відповідає одне значення у. Функцію у



Означення 2. Величина, числове значення якої при розглядає&

мих умовах не змінюється, називається постійною.

Змінною величиною називається величина, яка при умовах, що

розглядаються

, може приймати різні числові значення.

До основних характеристик змінної величини відносяться: непе!

рервність або дискретність, монотонність, обмеженість (повна або

часткова

) або необмеженість.

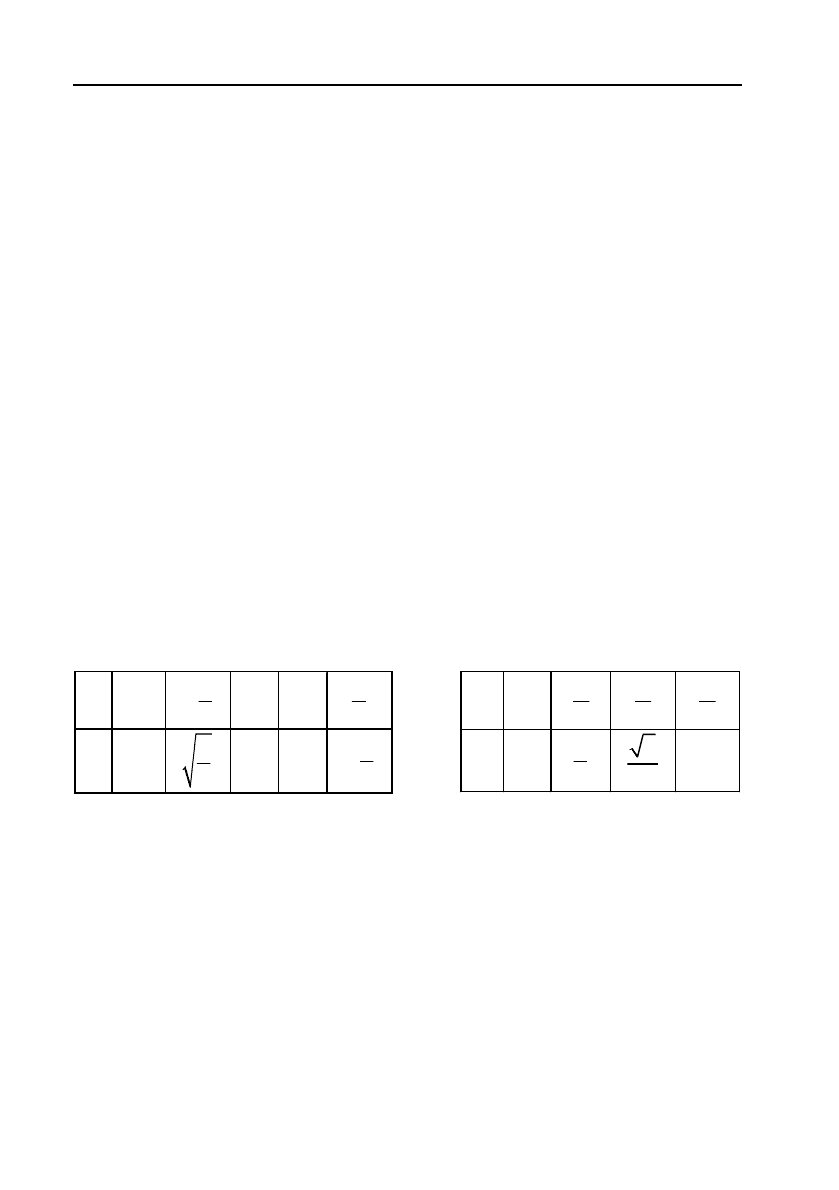
188

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

називають багатозначною, якщо кожному значенню х відповідає дек&

ілька значень у.

Існує декілька способів задання функції: аналітичний, табличний,

графічний, мовний та програмний. В математиці найчастіше вико!

ристовують перші три способи, тому детально їх розглянемо.

При аналітичному способі функція задається однією або декіль!

кома рівностями, що зв’язують залежні та незалежні змінні.

Наприклад:

а) 3х – 2у = 6; b) у = 3х

– 4; с)

21, 0

0, 0 1

3, 1

















Якщо рівняння, що зв’язує аргумент х з функцією у, не розв’яза!

но відносно у, а задано у вигляді F(x, у) = 0 (випадок а)), тоді змінну

називають неявною функцією х.

При табличному способі функціональна залежність задається

вигляді таблиці, в якій для кожного числового значення х вказано

відповідне

числове значення у. Наприклад:

Цей спосіб дуже часто використовується в економіці.

Графічний спосіб найбільш наглядний і базується на застосу!

ванні методу координат. При цьому способі функціональна за!

лежність зображується лінією, яку називають графіком функції.



Зауваження 1. Якщо функція задана аналітично, тобто за

допомогою

деякої формули, то неважко перейти до табличного або

графічного

способу завдання цієї функції. Перехід від табличного або

графічного

способів завдання функції до аналітичного способу потре&

бує певних знань та навичок. Іноді такий перехід вдається здійснити

лише

наближено.

x 0



y 0

або

x –1



0 1

y 3

0 –3



189

Частина 7. Вступ до математичного аналізу

7.1.3. Деякі властивості функцій

Функція є змінною величиною, тому вона може бути монотон

ною або не монотонною, обмеженою (зверху або знизу, або зверху та

знизу) або необмеженою. Крім цих властивостей часто використову

ють властивості парності та періодичності.



Означення 5. Функція у = f(x) називається парною, якщо

 

x

, тобто при заміні х на (–х) функція не змінюється.

Функція у = f(х) називається непарною, якщо f(–х) = –f(х), тобто

при заміні х на (–х) функція лише змінює свій знак на протилежний.

Відмітимо, що графіки парних функцій симетричні відносно осі ор

динат, а непарних функцій – симетричні відносно початку координат.

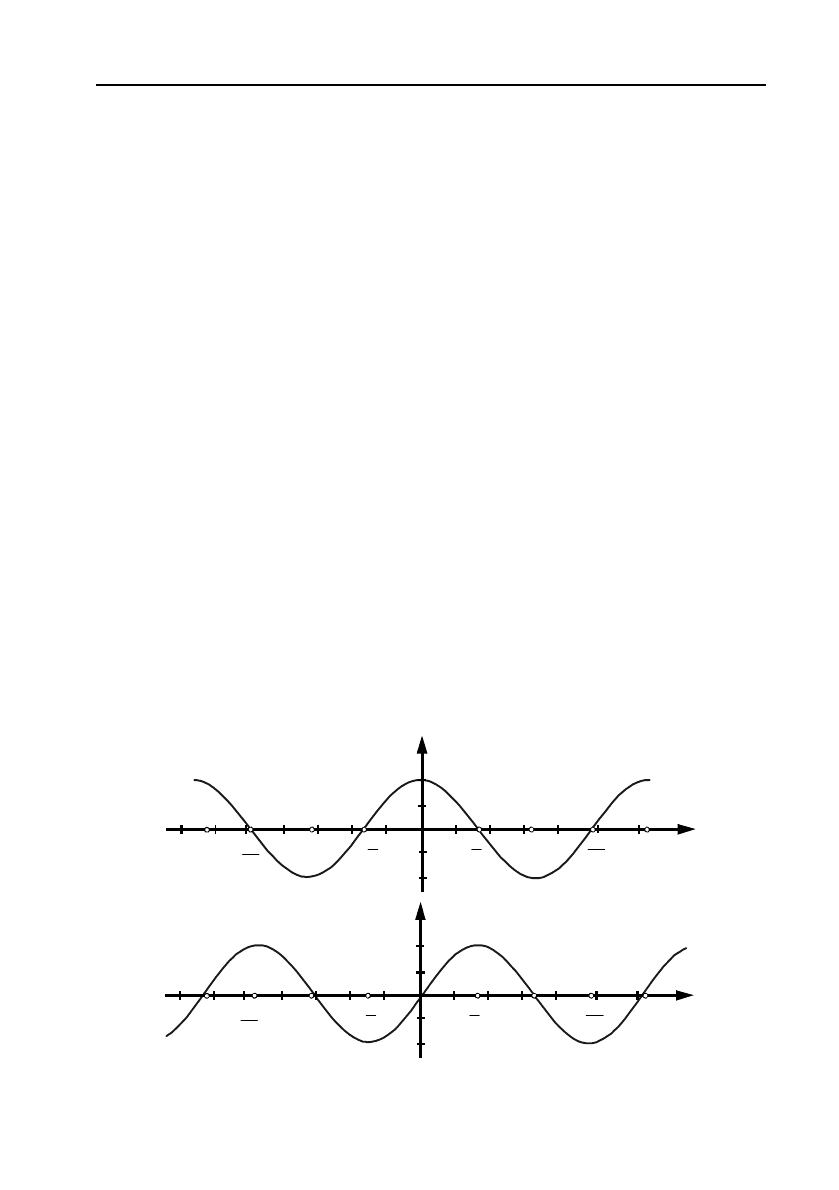
Наприклад, функція y = cosx є парною функцією тому, що

cos(–x) = cosx, а її графік є симетричним відносно осі Оу. Функція

y = sinx є непарною функцією тому, що sin(–x) = –sinx, а її графік є

симетричним відносно початку координат (див. мал. 1).



Означення 6. Функція у =f(х) називається періодичною,

якщо існує таке постійне число



, що виконується рівність







для будь#якого х.

Найменше додатне число



, що задовольняє цю рівність, нази

вають періодом функції. Наприклад, функції sinx та cosx періодичні

з періодом







. Функції tgx та ctgx періодичні з періодом







0,5

–0,5

–1

1234 5 6–6 –5 –4 –3 –2 –1–7

















y = sinx

Мал. 1.

0,5

–0,5

–1

1234 5 6–6 –5 –4 –3 –2 –1–7

















y = cosx

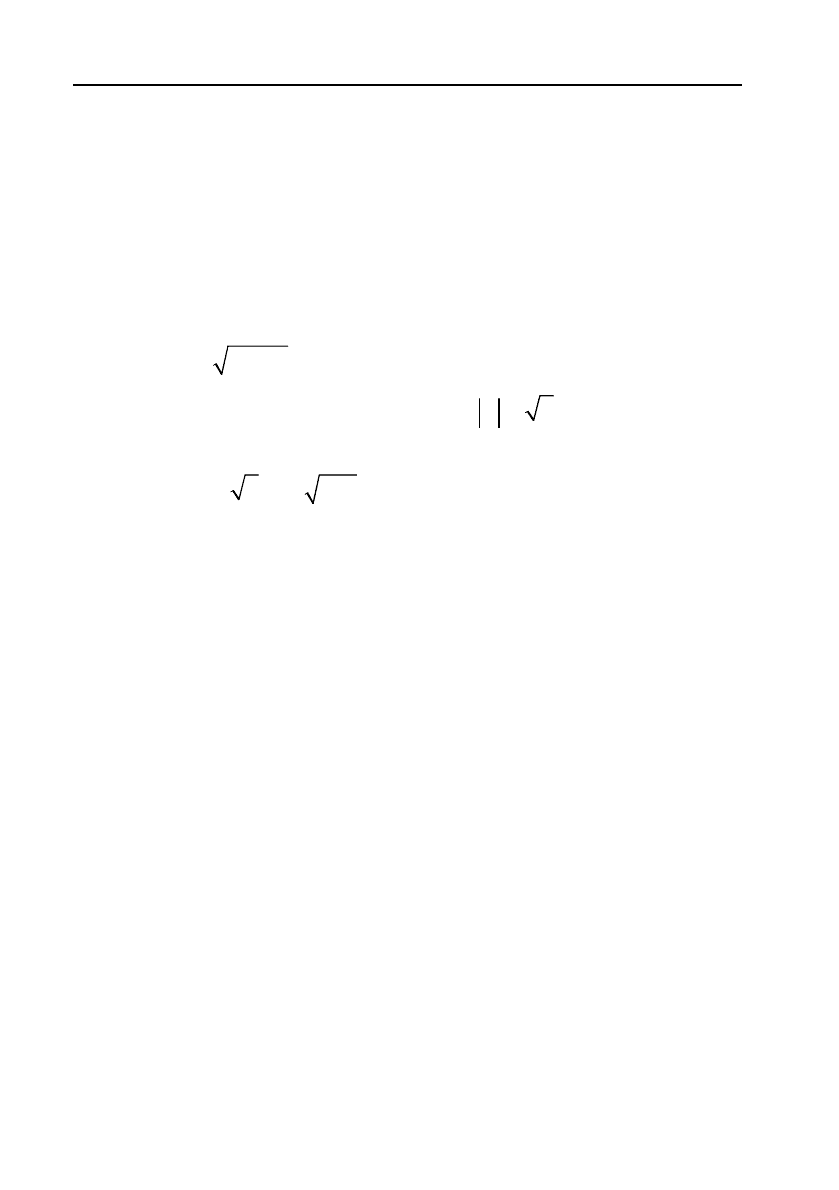
190

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

7.1.4. Області визначення та значень функції, заданої аналітично



Означення 7. Областю визначення функції називають су&

купність усіх тих значень аргументу

, для яких значення

, обчис&

лене за формулою, будуть певними дійсними числами.

Наприклад, якщо у = х

, то х може приймати будь!які значення,

тобто областю визначення цієї функції буде числова вісь



   

, символ



означає нескінченність).

Якщо



, то у приймає дійсні значення лише при

20 2 2xxx    .

Таким чином, областю визначення цієї функції буде об’єднання

областей

 

,2 2,.



  







Означення 8. Областю значень функції у = f(х) називають

сукупність

усіх значень

, коли

змінюється в області визначення

цієї

функції.

Так, для функцій sinx та cosx областю значень буде відрізок





1,1

7.1.5. Основні елементарні функції

1. Степенева функція



, де n – дійсне число.

2. Показникова функція у = а

, де а > 0,

1a 

3. Експоненціальна функція (показникова з а = e) у = е

, де



2,7182.

4. Логарифмічна функція

y = log

, де а > 0,

1a 

5. Натуральна логарифмічна функція



6. Тригонометричні функції:

y = sinx, y = cosx,

y = tgx, y = ctgx,

y = secx, y = cosecx.