Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


171
Частина 6. Векторна алгебра та аналітична геометрія
Використовуючи точки
1
M
та
2
,
M
аналогічно знаходимо рівнян!
ня прямої зростання врожайності зернових з одного гектара.
1980 8,5 1980 8,5
1995 1980 21 8,5 15 12,5
xzxz
12,5х – 1980
12,5 = 15z – 8,5
15
5z = 12,5x
12,5
1980 – 8,5
15
15z = 12,5x – 24877,5.
Отже, її кутовий коефіцієнт буде:
2
12,5
0,83
15
k
.
З умов задачі можна зробити висновок, що при зростанні трак!
торного парку врожайність зернових з 1 га зростає. Але кутовий
коефіцієнт
1
k
графіка зростання кількості тракторів значно більший
за
кутовий коефіцієнт
2
k
графіка зростання врожайності зернових.
Таким чином, зростання тракторного парка сприяє зростанню вро!
жайності зернових, але не пропорційно.
Зростання кількості тракторів – зростання енергоозброєності
сільського
господарства не є основним факторам у підвищенні ефек!
тивності сільського господарства. Необхідно враховувати вплив
інших
факторів, наприклад, якості насіння, культуру агротехніки.
b) Визначення рентабельності транспортного постачання
Транспортні
витрати перевезення одиниці вантажу (у) залізнич!
ним та автомобільним транспортом на відстань x знаходять за фор!
мулами:
1
10
2
yx
та
5
y
x
,
де х вимірюється десятками км.
Побудуємо графіки транспортних витрат перевезення (див. мал.
13).
Графіки прямих перетинаються в точці N(10, 15). Для перевірки
координат
точки N знайдемо точку перетину аналітично:
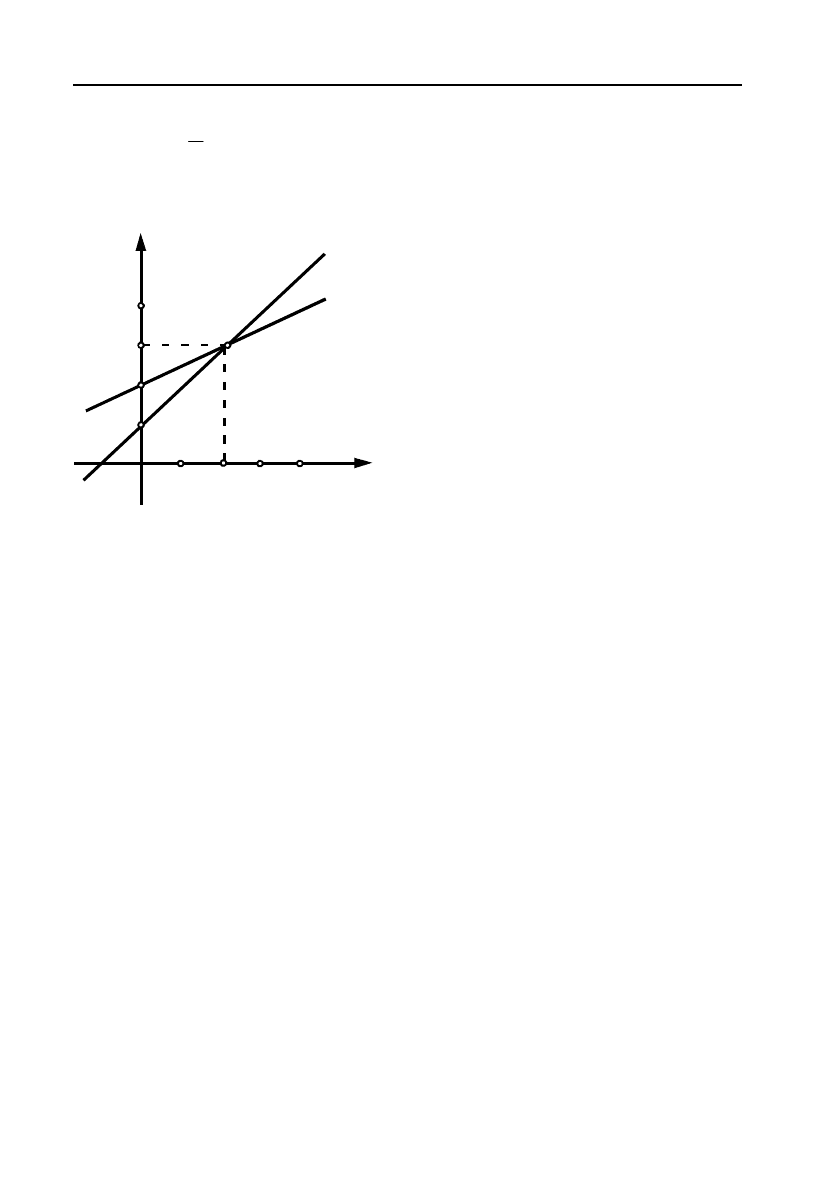
172
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
1
220
10
15; 10
2
5
5
xy
xy
yx
xy
xy
.
Графіки витрат дозволяють
зробити
висновок:
a)
коли
0,10x , тобто
х
< 100 км, транспортні витра!
ти у перевезення автотранс!
портом нижче витрат переве!
зення залізничним транспор!
том;
b)
коли
10, ,x
тобто
х
> 100 км, більш рентабельним
буде
залізничний транспорт.
с) Визначення витрат палива судном на підводних крилах
Дослідженням
виявлено, що витрати палива судном на підвод!
них крилах зростають пропорційно квадрату швидкості судна.
Треба знайти аналітичну залежність між витратами палива m та
швидкістю
судна V, враховуючи, що при V = 40 км/год витрачено
20 л палива за годину, а також визначити витрати палива за годину
при
швидкості 60 км/год.
Розв’язання. Згідно з умовою задачі шукану залежність можна
записати
у вигляді:
2
Vkm
,
де k – деякий коефіцієнт пропорційності.
Порівняння цієї формули з рівнянням параболи
2
y
= 2рх дозво!
ляє зробити висновок, що витрати палива змінюються за параболіч!
ним законом. При m = 0 швидкість V = 0, тобто парабола проходить
через
початок системи координат mОV. Згідно з умовою задачі пара!
бола проходить через точку М
0
(20, 40), тому її координати задоволь!
няють рівняння параболи:
Y
X
0
y = x/2 + 5
5
N
y = x + 5
Мал. 13.
10 15 20
5
10
15
20
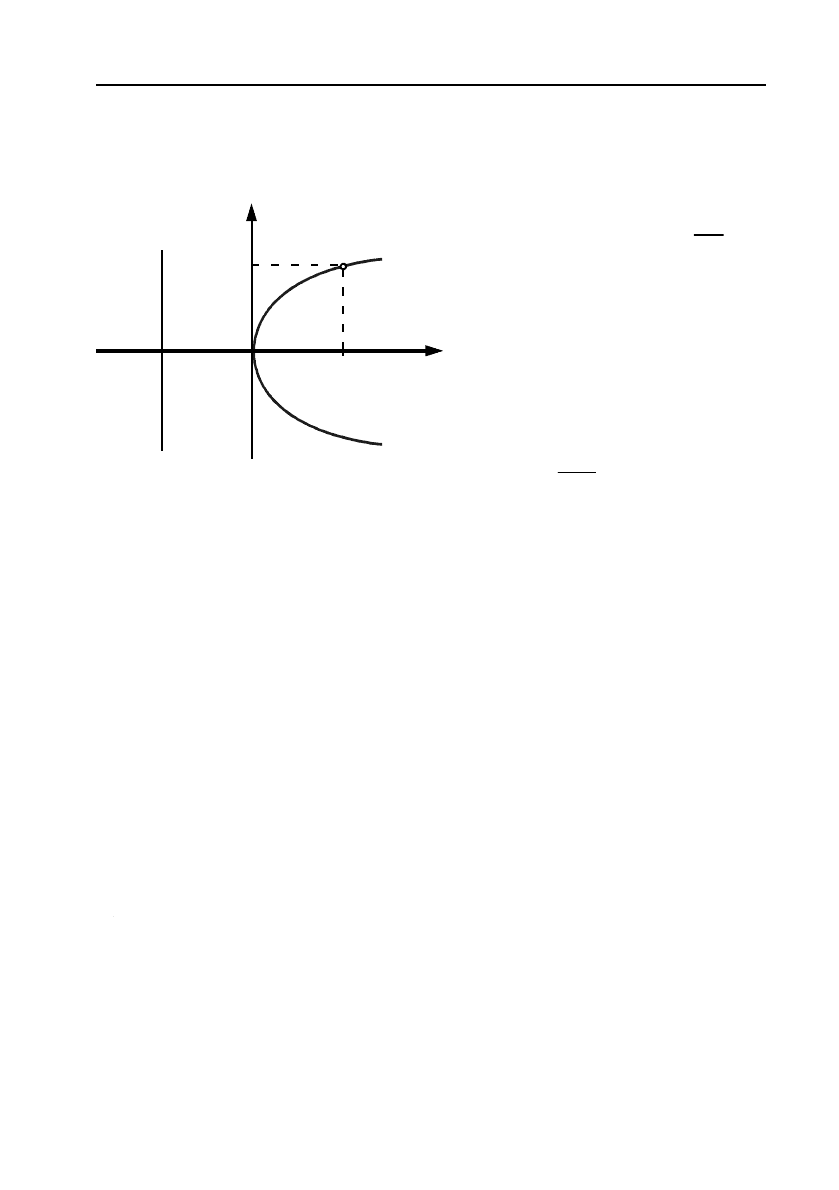
173
Частина 6. Векторна алгебра та аналітична геометрія
2
40 20 80kk
.
Таким чином, аналітична залежність між витратами палива та
швидкістю
судна буде:
2
2
80
80
V
Vmm .
Графік цієї залежності зоб!
ражено на малюнку 14. З ос!
танньої формули випливає,
що при швидкості 60 км/год
витрати
палива (у літрах) за
годину
повинні дорівнювати
2
60
45
80
m
(літрів).
d) Рівновага доходу та збитків
Компанія
виробляє вироби А та продає їх по 2 долари за кожний.
Керівництво компанії встановило, що сума
B
Y
загальних щотижне!
вих витрат (в доларах) на виготовлення виробів А кількістю х (ти!
сяч одиниць) має таку закономірність
Y
B
= 1000 + 1300x + 100x
2
.
Визначити щотижневу кількість виготовлення та продажу виробів
А
, яка забезпечує рівновагу витрат та доходу.
Розв’язання. Доход від продажу х тисяч виробів А вартістю 2
долари за кожний буде:
Д
Y
= 2000х.
Для рівноваги доходу та витрат треба щоб виконувалась рівність:
22
1000 1300 100 2000 7 10 0
BД
YY x x xx x
12
250 2;5xx x x
.
Отже, ця задача має дві точки рівноваги. Компанія може вироб!
ляти 2000 (х = 2) виробів А з доходом та витратами 4000 доларів,
або 5000 (х = 5) виробів з доходом та витратами 10000 доларів.
V
m
0
Мал. 14.
M
0
F
20
–20
40
174
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
6.2.7. Рівняння прямої та площини в просторі
а) Рівняння площини, що проходить через задану точку
M
0
(x
0
, y
0
, z
0
) перпендикулярно заданому вектору
n
= (А, В, С)
(
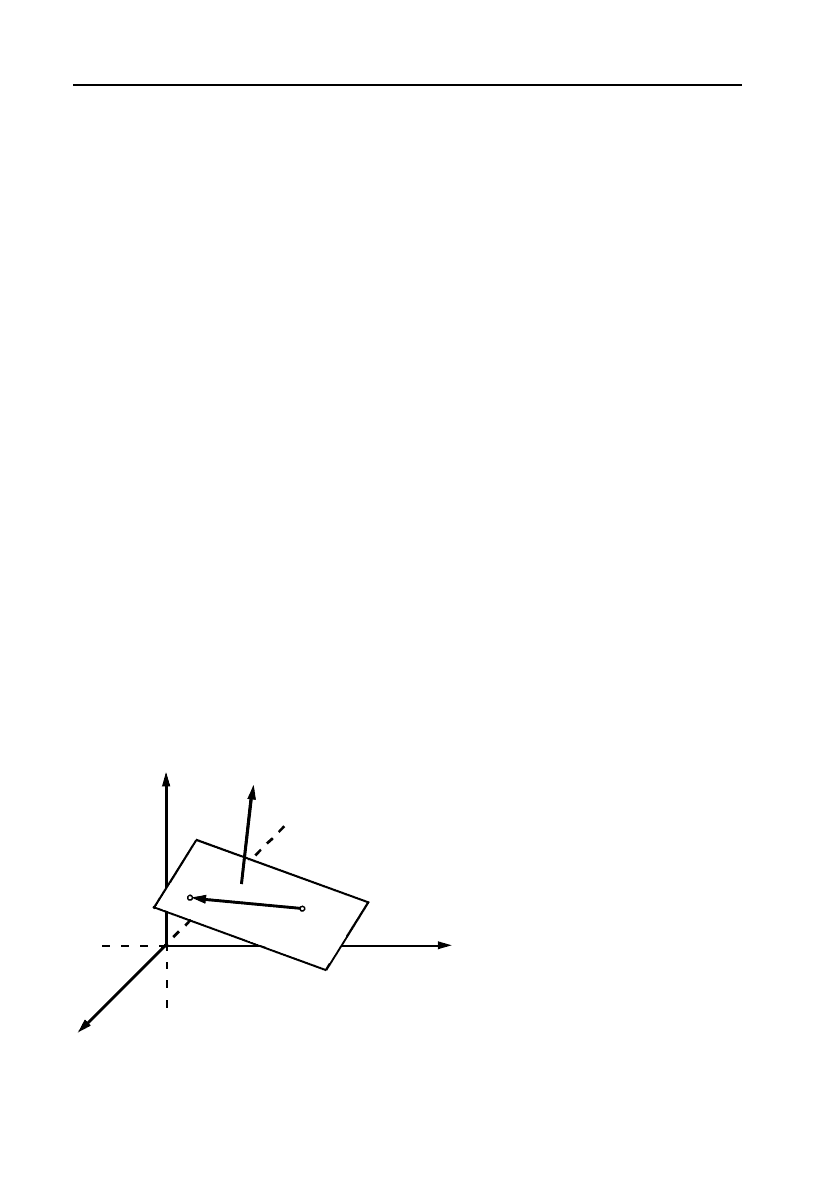
мал. 15).
Візьмемо довільну точку площини М(x, y, z) і побудуємо вектор
0
M
M
= (x–x
0
, y–y
0
, z–z
0
).
Вектори
0
MM
та
n
перпендикулярні, тому їх скалярний добу!
ток дорівнює нулю. Отже, маємо:
А(х–х
0
) + В(у–y
0
) + C(z–z
0
) = 0. (35)
Координати довільної
точки
М, що лежить в пло!
щині, задовольняють рів!
ність (35), а координати
точки
М, що не лежить в
площині
, не задовольняють
рівність
(35). Отже, рів!
ність (35) є рівнянням пло!
щини в просторі.
Розглянемо на цьому прикладі можливості компанії. Позначимо
щотижневий
прибуток Р, тоді
2
2000 1000 1300 100
Д B
PY Y x x x
2
1000 700 100 100 2 5xx xx
.
З останньої рівності випливає, що при х = 2 або х = 5 маємо Р = 0,
тобто ці значення х будуть точками рівноваги.
Коли 2 < х < 5, тоді х – 2 > 0, х – 5 < 0 і маємо Р > 0, тобто
компанія
одержить прибуток. При інших значеннях х, тобто коли
х
[2, 5] будемо мати Р < 0 – компанія несе збитки.
Мал. 15.
Y
X
Z
M
0
0
n
M

175
Частина 6. Векторна алгебра та аналітична геометрія
b)
Теорема. Будьяке рівняння першого степеня відносно
x, y, z визначає площину
.
Доведення. Розглянемо довільне рівняння першого степеня віднос!
но х, у, z:
Ax + By + Cz + D = 0. (36)
Це рівняння має нескінченну кількість розв’язків. Нехай
000
,,
xy
z
один з цих розв’язків. Тоді маємо:
Ах
0
+ Ву
0
+ Cz
0
+ D = 0. (37)
Різниця рівнянь (36) та (37) має вигляд:
А(х – х
0
) + В (у – у
0
) + С (z – z
0
) = 0. (38)
Ліву частину цієї рівності можна розглядати як скалярний добу!
ток векторів
n
= (А, В, С) та
0
M
M
= (х – х
0
, у – у
0
, z – z
0
).
З рівності нулю скалярного добутку випливає, що
0
.nMM
Отже, кінці вектора
0
M
M
лежать в площині, перпендикулярній
n
і яка проходить через точку М
0
, тобто рівняння (38), а значить і (36),
визначає площину перпендикулярну вектору
n
.
Означення 8. Рівняння вигляду (36) називають загальним
рівнянням площини в просторі.
Дослідження загального рівняння площини дозволяє визначити
її
положення в просторі. Так, рівняння вигляду
Ax + By + Cz = 0 (D = 0)
визначає площину, що проходить через початок координат; рівняння
вигляду
Ах + Ву = 0 в просторі визначає площину, яка паралельна осі
Oz і проходить через початок координат; рівняння х = 0 визначає пло!
щину yOz; у = 0 визначає площину xOz; z = 0 визначає площину хOу.
Приклад 1. Задані точки М
0
(4, 6, 1), М
1
(1, 0, –2), М
2
(4, –2, 4).
Треба:
a)
скласти рівняння площини, що проходить через точку М
0
пер!
пендикулярно відрізку М
1
М
2
;
b)
одержане рівняння звести до загального вигляду;
c)
побудувати цю площину в системі Оxyz.
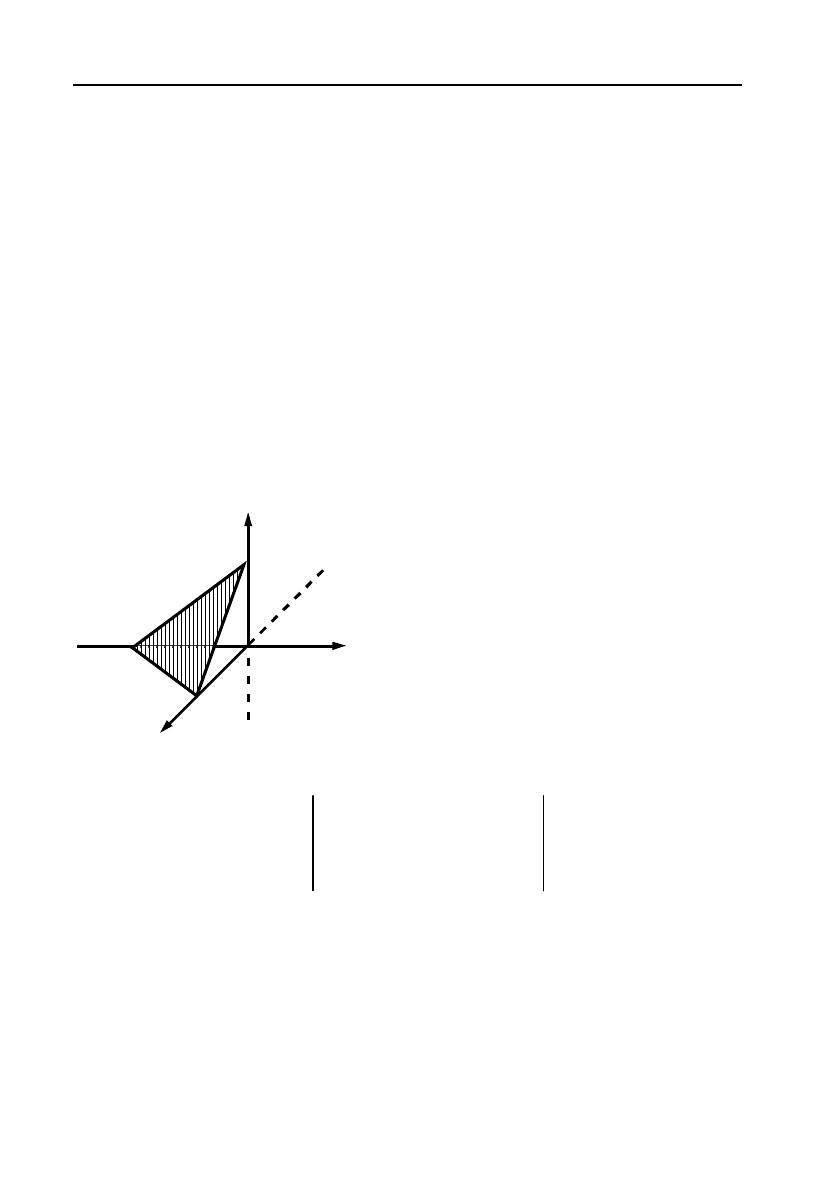
176
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Розв’язання.
а) Спочатку знайдемо координати вектора:
n
=
12
MM
= (4 – 1, –2 – 0, 4 – (–2)) = (3, –2, 6).
Підставивши координати вектора
n
та точки М
0
в рівняння (35),
одержимо:
3(x – 4) – 2(y – 6) + 6(z – 1) = 0.
b)
В одержаному рівнянні розкриємо дужки, тоді
3х – 12 – 2у + 12 + 6z – 6 = 0
3х – 2у + 6z – 6 = 0.
с) Для побудови площини в просторі знайдемо точки перетину
площини
з осями координат, тоді побудуємо площину по 3!х точках:
При х = 0, у = 0 маємо 6z – 6 = 0
z = 1.
При х = 0, z = 0 маємо – 2у – 6 = 0
у = –3.
При у = 0, z = 0 маємо 3х – 6 = 0
х = 2.
Побудуємо в системі координат ці
три
точки (див. мал. 16).
Задана рівнянням площина прохо!
дить через точки М
3
(0, 0, 1), М
4
(0, –3, 0),
М
5
(2, 0, 0) і на мал. 16 заштрихована.
Зауваження 1. Рівняння площи&
ни, що проходить через три точки
M
1
(x
1
, y
1
, z
1
), M
2
(x
2
, y
2
, z
2
), M
3
(x
3
, y
3
, z
3
)
знаходять за формулою:
111
212121
313131
0
xx yy zz
xxyyzz
xxyyzz
. (39)
с) Канонічні та параметричні рівняння прямої в просторі
Нехай
здана точка М
0
(х
0
, у
0
, z
0
) на прямій L та вектор
s
=(l, т, р)
паралельний прямій. Знайдемо рівняння цієї прямої.
Візьмемо довільну точку M(x, y, z) на прямій і розглянемо вектор
0000
,,
M
Mxxyyzz
(мал. 17).
Y
X
Z
2
1
0
–3
Мал. 16.

177
Частина 6. Векторна алгебра та аналітична геометрія
Вектори
0
M
M
та
s
пара!
лельні, тому їх координати
пропорційні
,
000
x
xyyzz
lmp
. (40)
Якщо точка М не нале!
жить прямій L, тоді координа!
ти цих векторів не про!
порційні і (40) не має місця.
Отже, співвідношення (40) є
рівняннями
прямої L, які на!
зивають канонічними рівняннями прямої. Вектор
s
називають на
прямним вектором прямої
.
Позначимо через t загальне значення відношень канонічних
рівнянь
прямої L:
000
xx yy zz
t
lmp
.
Звідси одержуємо:
0
0
0
x
xlt
y
ymt
z
zpt
. (41)
Ці рівняння називають параметричними рівняннями прямої в
просторі
, яка проходить через точку M
0
(x
0
, y
0
, z
0
) паралельно векто!
ру
,,slmp
.
В рівняннях (41) t розглядають як параметр, що довільно
змінюється
в інтервалі
,.
Координати х, у, z точки М залежать
від
t, тому при зміні t точка М(х, у, z) рухається по прямій L.
d) Рівняння прямої, що проходить через дві точки
Нехай
на прямій задані дві точки
1111
,,
Mx
y
z
,
2222
,,
M
x
y
z
.
M
Y
X
Z
M
0
0
s
L
Мал. 17.

178
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Знайдемо рівняння такої прямої. Нехай напрямним вектором
прямої
буде вектор
12 2 12 12 1
,, .
s
MM x x y y z z
Тоді, підстав!
ляючи координати вектора
s
в рівняння (40), одержимо рівняння
111
21 21 21
xx yy zz
xx yy zz
, (42)
яке називають рівнянням прямої, що проходить через дві задані
точки
1
M
та
2
M
.
Приклад 2. Скласти канонічні та параметричні рівняння пря!
мої, що проходить через точки
1
M
(3, –5, 2) та
2
M
(1, –1, –4).
Розв’язання. За формулами (42) маємо:
35 2 352
13 15 42 2 4 6
xy z xyz
або
352
123
xyz
це канонічні рівняння прямої.
Для одержання параметричних рівнянь цієї прямої використовує!
мо формули (41), тоді:
3
52 ,
23
xt
ytt
zt
.
d) Деякі важливі формули
Вкажемо
деякі формули, які можуть бути корисними при розв’я!
зуванні багатьох задач і які доведені у більш повному курсі аналі!
тичної геометрії.
1.
Відстань d від точки М
0
(х
0
, у
0
, z
0
) до площини, заданої загаль!
ним рівнянням Ах + By + Cz + D = 0, знаходять за формулою
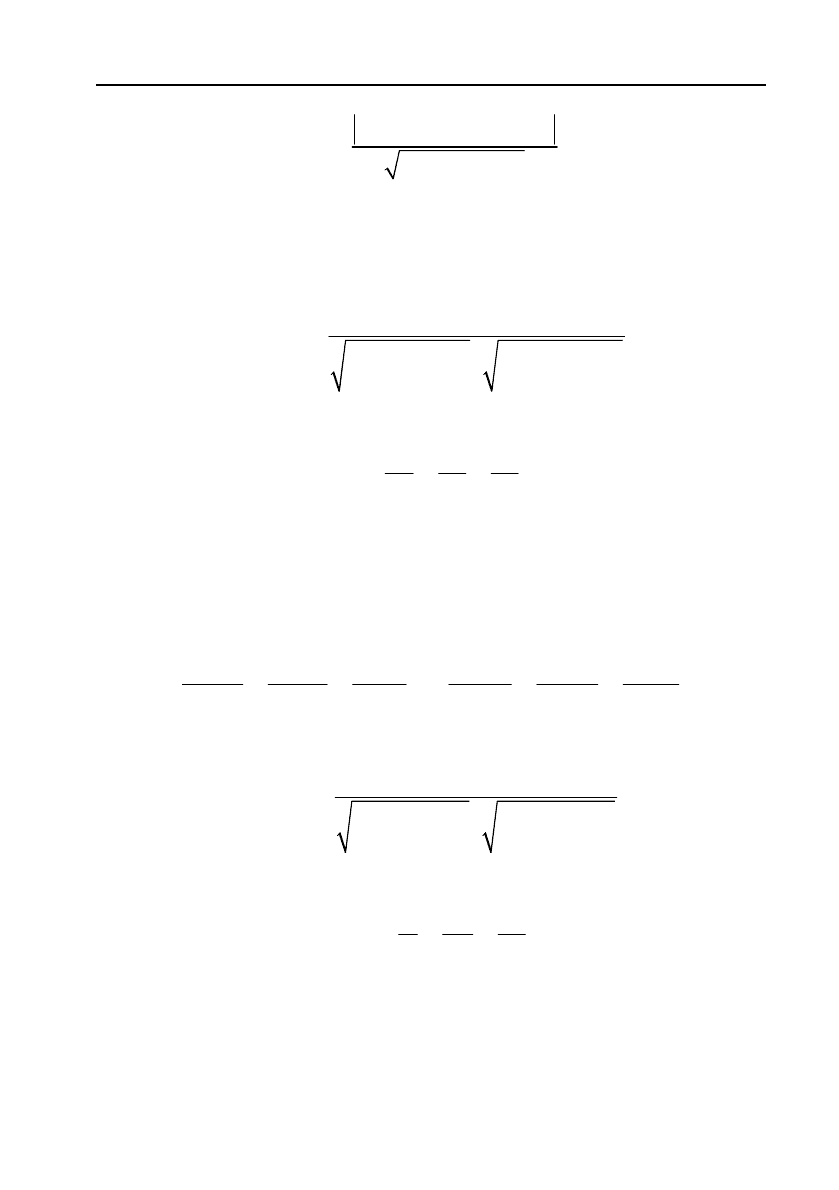
179
Частина 6. Векторна алгебра та аналітична геометрія
000
222
A
xByCzD
d
ABC
. (43)
2.
Косинус кута
між двома площинами, що задані загальними
рівняннями
1111
0Ax By Cz D
,
2222
0Ax By Cz D
, зна!
ходять за формулою:
12 12 12
222 222
111 222
cos
AA BB CC
A
BC ABC
. (44)
Умова паралельності площин має вигляд:
111
222
A
BC
A
BC
. (45)
Умова перпендикулярності площин:
12 12 12
0AA BB CC
. (46)
3.
Косинус кута
між двома прямими, заданими канонічними
рівняннями
:
111
111
x
xyyzz
lmp
та
222
222
x
xyyzz
lmp
знаходять за формулою:
12 1 2 1 2
222222
111222
cos
ll mm pp
lmp lmp
. (47)
Умова паралельності прямих має вигляд:
111
222
lmp
lmp
. (48)
Умова перпендикулярності прямих:
12 1 2 1 2
0ll mm pp
. (49)

180
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
6.2.8. Поверхні другого порядку
Означення 9. Поверхні в просторі називаються поверхнями
другого порядку
, якщо їх рівняння містять хоча б одну з координат
х
, у, z у другому степені.
Вкажемо визначення та рівняння деяких поверхонь в просторі.
а) Сфера та її рівняння
Означення 10. Сферою називають геометричне місце точок,
рівновіддалених від заданої точки – центра сфери.
Якщо центром сфери є
000
,,
Cx
y
z
, а радіус R, тоді рівнянням
сфери
буде:
222
2
000
xx yy zz R
. (51)
Означення 11. Поверхня називається циліндричною, якщо вона
утворена
прямою (твірна), паралельною до заданої прямої L і яка
проходить
через задану лінію l (напрямна лінія).
Приклад 3. Знайти точку перетину прямої
234
112
xyz
та площини 2x + y + z – 6 = 0.
Розв’язання. Шукані координати точки перетину (х, у, z) по!
винні задовольняти рівнянням прямої та площини. Параметрични!
ми рівняннями заданої прямої будуть
2
3
42
xt
y
t
zt
. (50)
Підставимо ці х, у та z в рівняння площини:
2(2 + t) + (3 + t) + (4 + 2t) – 6 = 0
5t + 5 – 0
t = –1.
Підставивши знайдене t в формули (50), одержимо координати
точки
перетину:
х = 2 – 1 = 1; у = 3 – 1 = 2; z = 4 – 2 = 2.
Отже, точкою перетину буде М(1, 2, 2).
