Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

281

Частина 9. Функції кількох змінних



Наслідок. Точки, в яких



1, 2,...,







не існують або

дорівнюють

нулю називають критичними точками або підозріли

ми на екстремум.



Приклад 7. Знайти критичні точки функції

321zx x





Розв’язання Спочатку знайдемо частинні похідні першого по!

рядку заданої функції двох змінних:

23;

zxy





zxy



  

Ці похідні існують для усіх

та

, тому критичними будуть

лише

точки, де частинні похідні дорівнюють нулю, тобто





















 





Остання система лінійна, неоднорідна, з двома невідомими. Роз!

в’язуючи систему за правилом Крамера, одержимо:

;





Отже, критичною точкою буде



M 

9.4.2. Знаходження екстремуму функцій двох змінних

Необхідні

умови існування екстремуму функцій кількох змінних

дозволяють

знаходити лише критичні точки.

У випадку функції двох змінних за допомогою достатніх умов

існування

екстремуму можна перевірити кожну критичну точку та

виявити

, який саме екстремум існує в цій точці.



Теорема. (Достатні умови існування екстремуму). Нехай

в околі критичної точки



00 0

функція



,zfxy

має

неперервні частинні похідні до другого порядку включно

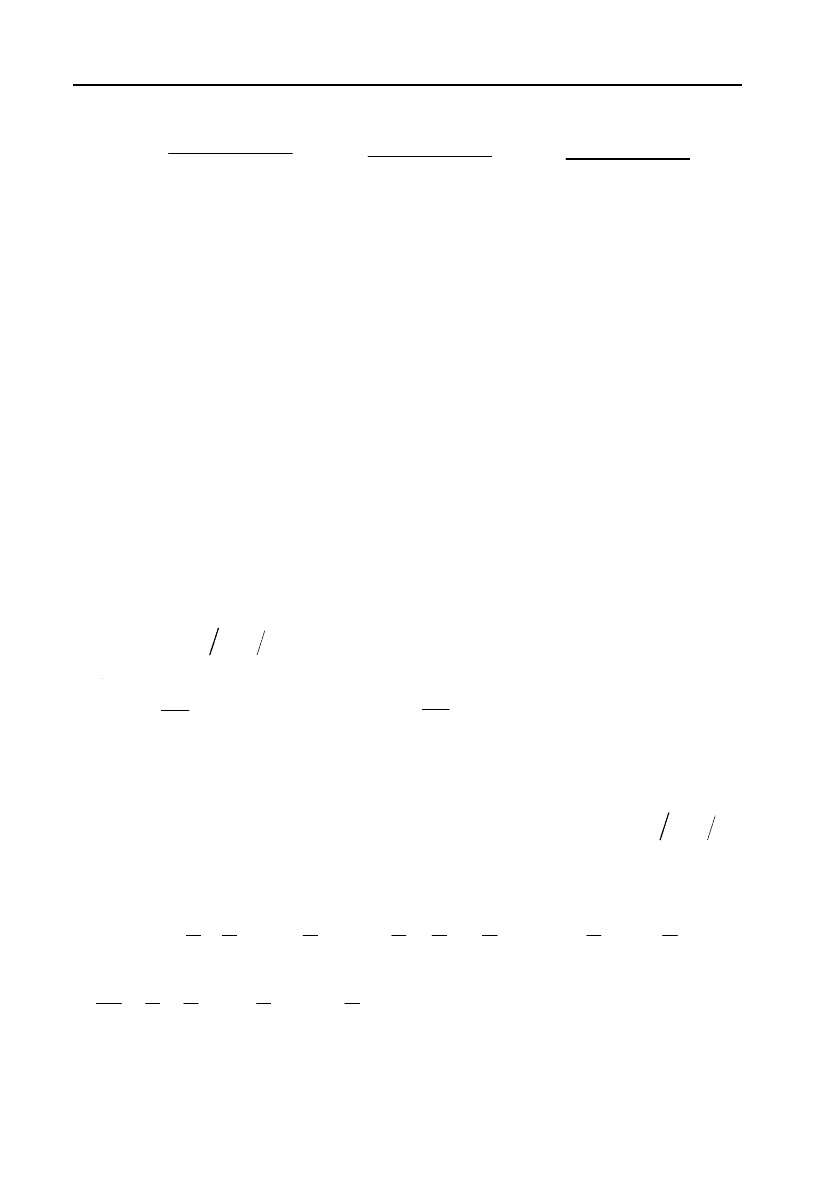
282

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



;

fx y









;









fx y







Тоді:



,fxy

має максимум, якщо

11 22 12

0aa a

та



;



,fxy

має мінімум, якщо

11 22 12

0aa a

та



;



,fxy

не має екстремуму, якщо

11 22 12

0aa a

;

4) якщо

11 22 12

0aa a

, тоді екстремум в точці

може

існувати, а може і не існувати, тобто в цьому випадку треба

використовувати іншу достатню ознаку.



Приклад 8. Дослідити на екстремум функцію

321

xxyy xy





Розв’язання. У прикладі 7 для цієї функції знайдена критична

точка



43,13M



. Застосуємо достатню умову. Маємо:



232;

zxy











231;

zxy













Тому



11 22 12

22 1 3 0aa a



та

20a



Згідно з другим твердженням теореми в точці



43,13M



задана функція має мінімум:

min

41 4 4 1 1 4 1

,321

33 3 3 3 3 3 3

1641 2 4

41.

999 3 3

   

    

   

   



283

Частина 9. Функції кількох змінних

9.4.3. Знаходження умовного екстремуму методом Лагранжа

Екстремум

функції





при виконанні умови



,0xy





називають умовним екстремумом функції.

Умовні екстремуми часто використовуються при дослідженні

оптимізації

багатьох економічних та соціальних проблем.

Для знаходження умовного екстремуму методом Лагранжа треба:

записати функцію Лагранжа вигляду

  

,, , ,

xy fxy xy





;

знайти критичні точки



kk k k

Mx y



функції Лагранжа,

використовуючи необхідні умови існування екстремуму:



xxx

yyy























































;

перевірити в кожній критичній точці достатні умови існуван!

ня екстремуму:

а) якщо в точці



kk k k

Mx y



визначник третього порядку



 

  

xk yk

kxkxxkxyk

kxykyyk

MMLMLM

MLMLM







 



 

додатний, тоді точка

є точкою максимуму і



max

kkk



;

284

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

б) якщо визначник



M

тоді точка

є точкою мініму!

му і



min ,

kkk

fM fx y





Приклад 9. Знайти екстремум функції



при умові що

2xy





Розв’язання. Будемо шукати умовний екстремум з використан!

ням функції Лагранжа



2Lxy x y



 

Необхідні умови існування тепер мають вигляд



















Виключаючи з цієї системи



одержимо:

22 2

22 22

20 0 1

20 0

xy xy x

xy xy

















































 













Отже, критичними точками будуть:



1, 1 ,M 



1, 1 ,M 



1, 1 ,M 



1, 1M

Для перевірки достатніх умов існування екстремуму запишемо

визначник

в довільній точці



враховуючи























;









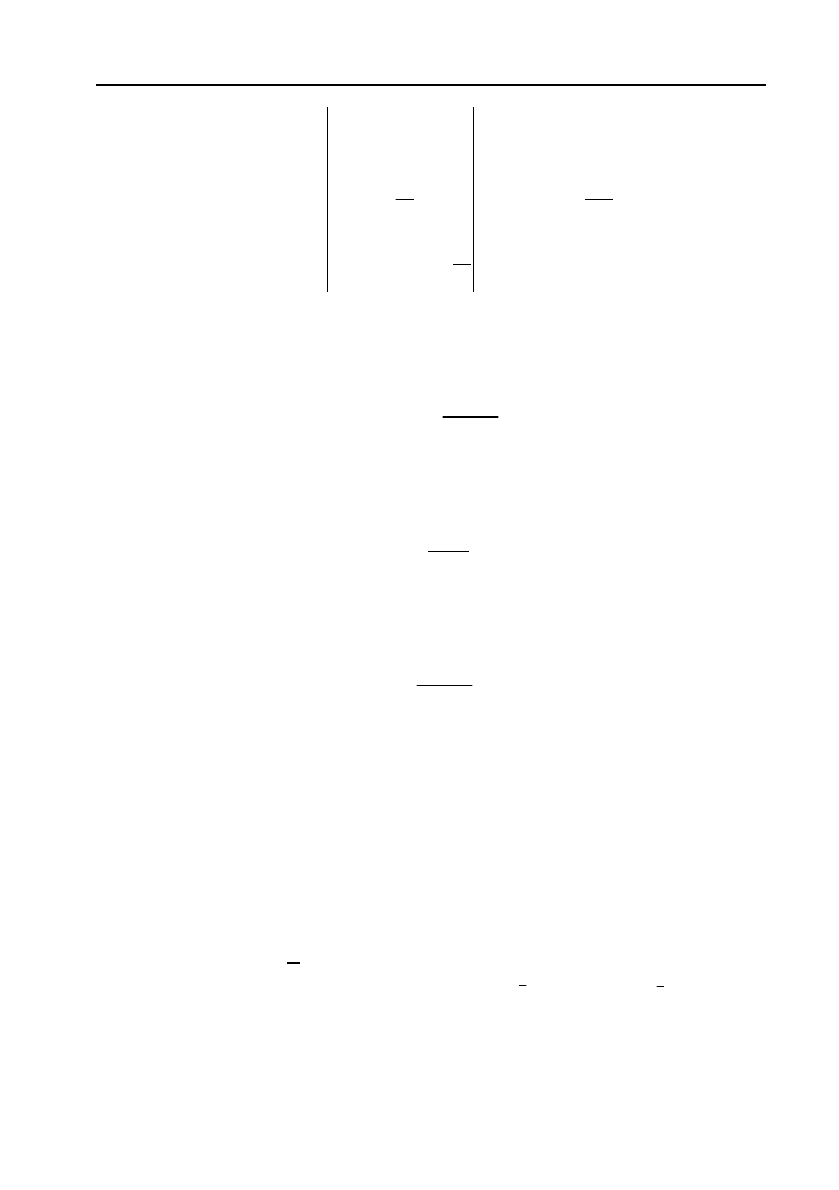
285

Частина 9. Функції кількох змінних



02 2

21124.

Mx xy

   



Тепер можна знайти значення цього визначника в кожній кри!

тичній точці і використати достатні умови:

  



12 1 1 4 12 4 16 0



 



 

max 1

111.zzM

 



12 1 1 4 12 4 16 0

 





min 2

11 1.zzM

 



12 1 1 4 12 4 16 0



 



min 3

11 1.zzM



12 4 16 0M



max 4

11 1.zzM

9.4.4. Найбільше і найменше значення функції в замкненій області

Для

знаходження найбільшого та найменшого значень функцій у

замкненій

області

які позначаються



max , ,



min , ,

відповідно, треба знайти екстремальні значення функції в точках, що

лежать

всередині

та на межі області, і обрати найбільше та най!

менше значення.

286

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



Приклад 10. Знайти найбільше та найменше значення функції





в трикутнику, обмеженому лініями







Розв’язання. Спочатку знайдемо критичні точки всередині об!

ласті:

  

24 832





  

222

442





Згідно з необхідними умовами існування екстремуму функції двох

змінних

маємо систему рівнянь



83 2 0

420

xy x y

xxy



 





 





Всередині області

0x 

та,



тому

328 2

24 1

xy x

xy y

 







 



В критичній точці



2, 1M

маємо



2, 1 4.z



Тепер проведемо дослідження функції на межі трикутника. На

прямій



змінна

x

і функція

приймає вигляд

  

64 62 6,zx x xx xx 

0, 6x











Знайдемо найбільше та найменше значення цієї функції однієї

змінної

на замкненому відрізку





0,6 :

624.zx x





Із рівності





знаходимо:

(

)

x 

, звідси випливає, що



та



. Отже,



464z 

. При

0x 

та

6x 



00z 



60.z 

На прямій



маємо



287

Частина 9. Функції кількох змінних

Отже, задана функція

має найбільше значення в точці



2, 1M

всередині області, найменше значення – в точці



4, 2M

на межі області.

Найбільше значення



max 2, 1 4;

zz

Найменше значення



min 4,2 64.

zz

9.5. Метод найменших квадратів

При дослідженні різних економічних та соціальних проблем час!

то одержують

значень величини

та відповідні їм значення ве!

личини

. Результати спостережень записують у вигляді таблиці

За

даними цієї таблиці необхідно визначити вигляд функціональ!

ної залежності між

та

, тобто від табличної форми завдання

функціональної

залежності необхідно перейти до аналітичної форми

її

завдання вигляду





Розв’язування цієї задачі можна розподілити на два етапи.

Спочатку, використовуючи графічне представлення точок

 

,1,2,,

kkk

Mxy k n





, обирають форму залежності між

та

тобто обирають вигляд функції





У випадку лінійної залежності (точки

мало відхиляються від

прямої

лінії) між

та

обирають такий вигляд функціональної

залежності

ax b



;

у випадку параболічної залежності:

ax bx c



;

у випадку гіперболічної залежності:



;



288

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

у випадку показникової залежності:



На цьому етапі параметри

та

– невідомі.

Нехай в результаті першого етапу розв’язування задачі обрана

залежність

вигляду



,,,,

yfx

 





з невідомими параметра!

ми

,,,

 



Для знаходження невідомих параметрів на другому етапі розв’я!

зання задачі будують функцію



,,,, ,

kk m

Syfx

 









(8)

залежну від

параметрів.

Ця функція дорівнює сумі квадратів відхилень точок



kkk

від обраної лінії, рівняння якої



,,,,

yfx

 





Будемо шукати такі значення параметрів

,,,

 



при яких

функція

приймає мінімальне значення, тому відхилення таблич!

них даних (точок



kkk

) від обраної функціональної залежності

(відповідної лінії) буде мінімальним.

Необхідна умова для існування екстремуму функції

– рівність

нулю

частинних похідних:









1, 2, ,im



. (9)

Ця умова є системою

алгебраїчних рівнянь з

невідомими.

Розв’язок системи (9) і дає найкращі значення шуканих параметрів.



Приклад 11. Величина товарообміну

(тисяч гривень) та вит!

рати обігу

(гривень) задані таблицею

Знайти

аналітичну залежність між

та

140

160

240

320

551

576

628,5

673

768,5

863

289

Частина 9. Функції кількох змінних



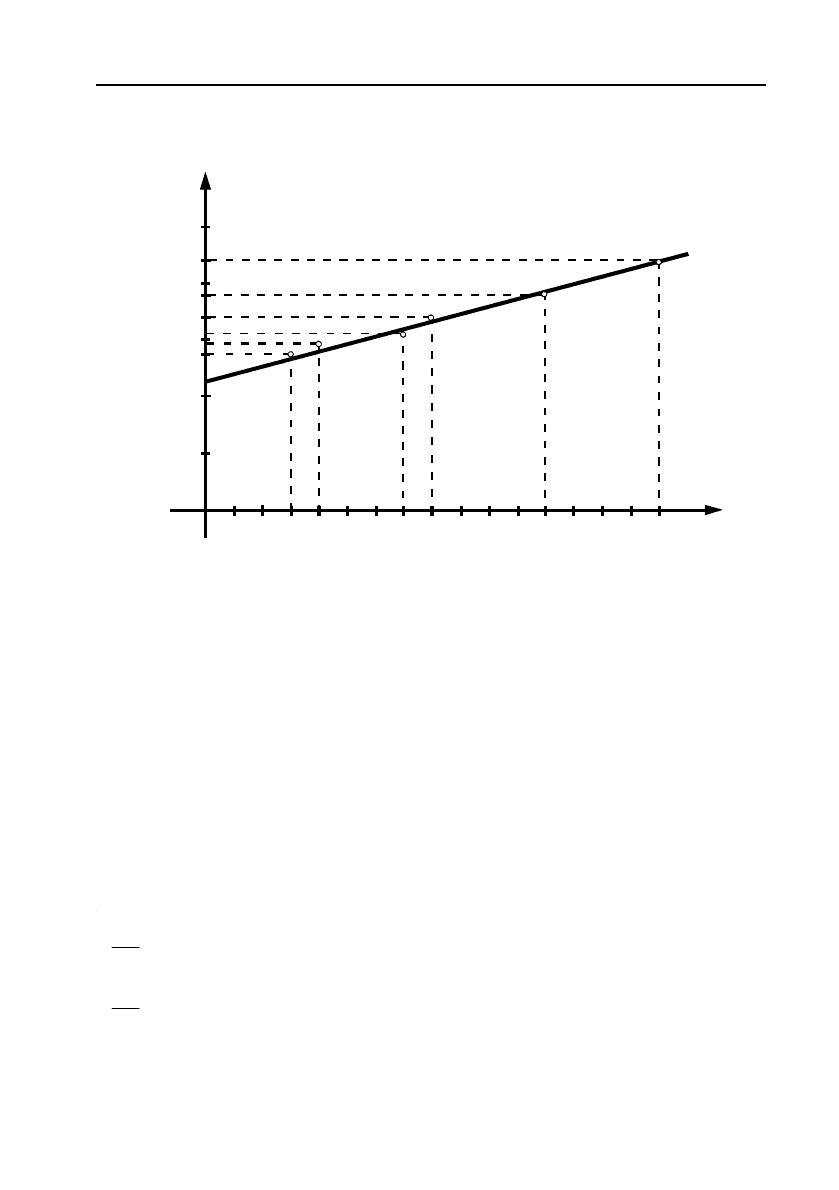
Розв’язання. Спочатку побудуємо у прямокутній системі ко!

ординат задані таблицею точки (див. мал. 3).

Малюнок дозволяє припустити існування лінійної залежності між

та

, тобто у вигляді:

ax b



Запишемо для цієї задачі функцію

за формулою (8):



Syaxb







Згідно з методом найменших квадратів параметри

та

по!

винні надавати мінімум функції

Використовуючи необхідну умову (9), одержимо



6666

1111

666

111

2106

kk k k k kk

kkkk

kk k k

kkk

ax b x a x b x y x

yaxb ax b y











   







 





 



 



 















Розв’язок цієї системи можна знайти за правилом Крамера:

20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320

200

400

600

800

1000

551

673

768,5

863

y = f(x)

Мал. 3.

290

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

666

111

kk k k

kkk

xy x y



























, (10)

66 6 6

11 1 1

kk kkk

kk k k

xy xyx

  



 

 

 

 













 



. (11)

Використовуючи значення

та

з таблиці, одержимо:

60 80 140 160 240 320 1000



 



551 576 628,5 673 768,5 863 4080







60 551 80 576 140 628,5 160 673 240 768,5

320 863 735410.



  

 





2222 22

60 80 140 160 240 320 215200



 



Підставимо ці значення у формули (10) та (11).

Тоді одержимо

6 735410 1000 4080 60 (73541 68000) 16623

6 215200 1000000 100(6 2152 10000) 14560

 



 

215200 4080 735410 1000 1000

(

2152 408 735410

)

6 215200 1000000 100(6 2152 10000)

356515

728

   



 

