Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


291
Частина 9. Функції кількох змінних
9.6. Питання для самоперевірки
1.
Якими міркуваннями треба керуватись для знаходження обла!
стей визначення та неперервності функції кількох змінних?
2.
Як позначають та знаходять частинні похідні першого та ви!
щого порядків, повний диференціал, повний приріст функції?
3.
Що характеризують і за якими формулами знаходять похідну
за
напрямом та градієнт функції трьох та двох змінних?
4.
Як визначають екстремуми функції кількох змінних, умовний
екстремум
?
5.
Як формулюють та використовують необхідні умови існуван!
ня екстремуму функції кількох змінних?
6.
Який мають вигляд і як формулюються достатні умови існу!
вання екстремуму функції двох змінних?
7.
Який вигляд мають необхідні та достатні умови існування
умовного
екстремуму функції двох змінних?
8.
Який порядок дій при знаходженні умовного екстремуму з
використанням
функції Лагранжа?
9.
Коли застосовують метод найменших квадратів?
10.
Чим керуються, коли обирають функціональну залежність
між
x
та
y
при переході від табличного задання функції до ана!
літичного?
11.
Мінімум якої функції треба знаходити при використанні ме!
тоду найменших квадратів?
Наближено можна вважати
1,13, 489,71.
ab
Отже, одержали функціональну залежність вигляду
1,13 489,71
y
x
.
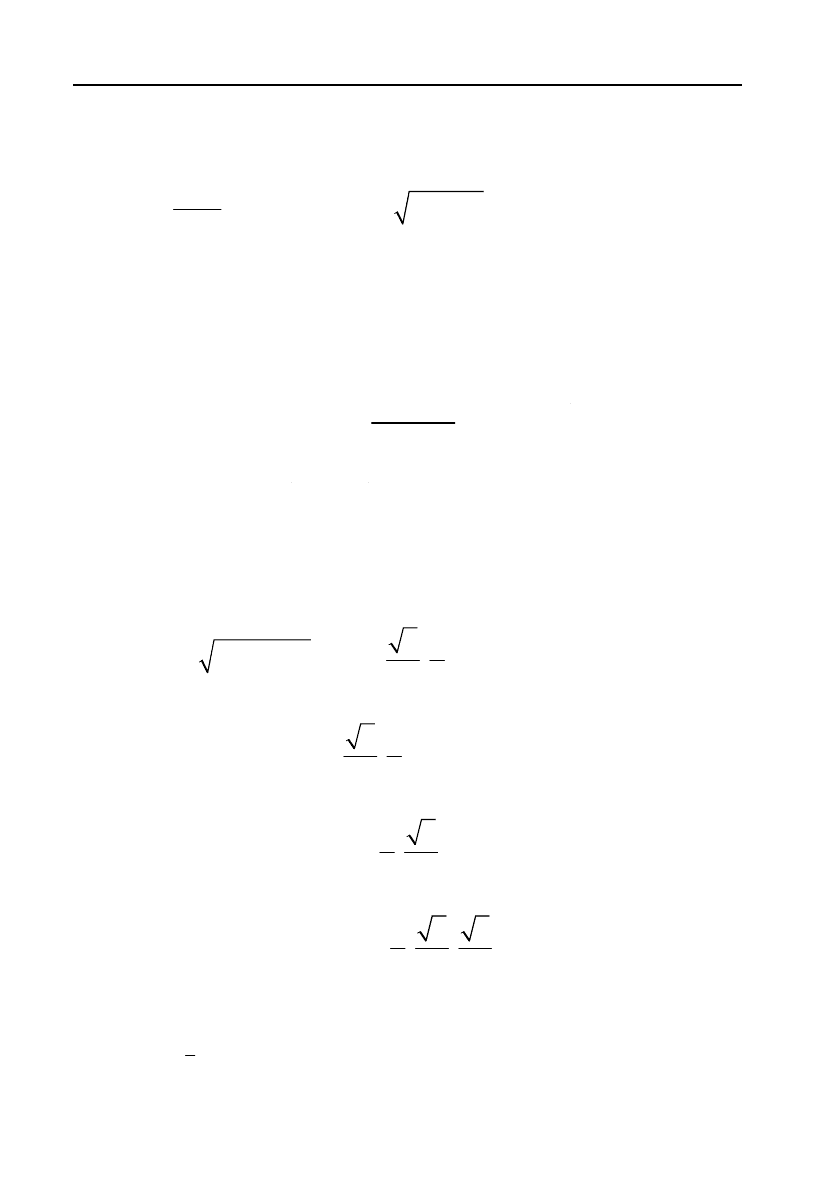
292
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
9.7. Вправи до розділів 9.2–9.5
1. Зайти усі похідні другого порядку функції:
a)
2
;
1
x
z
y
b)
22
;
zxy
c)
22
23;
z
xy y
d)
34
5310;
zx y
e)
2
ln ln ;
z
xyy x
f)
23
;
x
y
ze
g)
5
32.
zxy
2.
a)
Знайти похідні
y
xx
z
та
4
3
z
x
y
– функції
45
3.
z
xy
b) Знайти похідні
xyy
z
та
x
xy
z
– функції
2
2
.
x
y
zxe
3. Для заданої функції знайти похідну за напрямом
l
та градієнт
в
точці
0
M
:
a)
22
ln 2 2 ;
uxy
31
,,
22
l
0
1, 1 ;
M
b)
22
23;zx
y
31
,,
22
l
0
0, 2 ;
M
c)
33
3;ux y xy
13
,,
22
l
0
2,1 ;M
d)
232
32 ;ux yz
132
,, ,
22 2
l
0
2, 2,1 .M
4. Зайти повний диференціал функції
a)
;
x
y
ze
b)
2
2;uxy yzzx
c)
222
34 ;ux yz

293
Частина 9. Функції кількох змінних
d)
22
25 3;wx y x y
e)
22
1;
94
xy
z
f)
2
4;w
y
x
g)
22
ln 4 .uxy
5. Знайти екстремуми функцій
a)
22
9620;zx xyy x y
b)
22
2;
xy
z
ex
y
c)
2
2
()
x
z
ex
y
; d)
8 x
uy
xy
;
e)
33
3;wx y xy
f)
442 2
2;ux y x xyy
g)
23 2
334;zxx
yy
h)
32
31512.zx xy x y
6. Знайти умовні екстремуми функцій:
a)
z
x
y
при
22
111
;
2xy
b)
11
u
xy
при
320;
xy
c)
22
4zx y xyxy
при
30
xy
;
d)
2
wx
y
при
21
xy
;
e)
22uxyz
при
222
36.xyz
7. Знайти найбільше та найменше значення функції в області
D
.
a)
112;
z
xy
0; 0; 1 ;Dx y xy
b)
2
;zx
y
22
1.Dxy
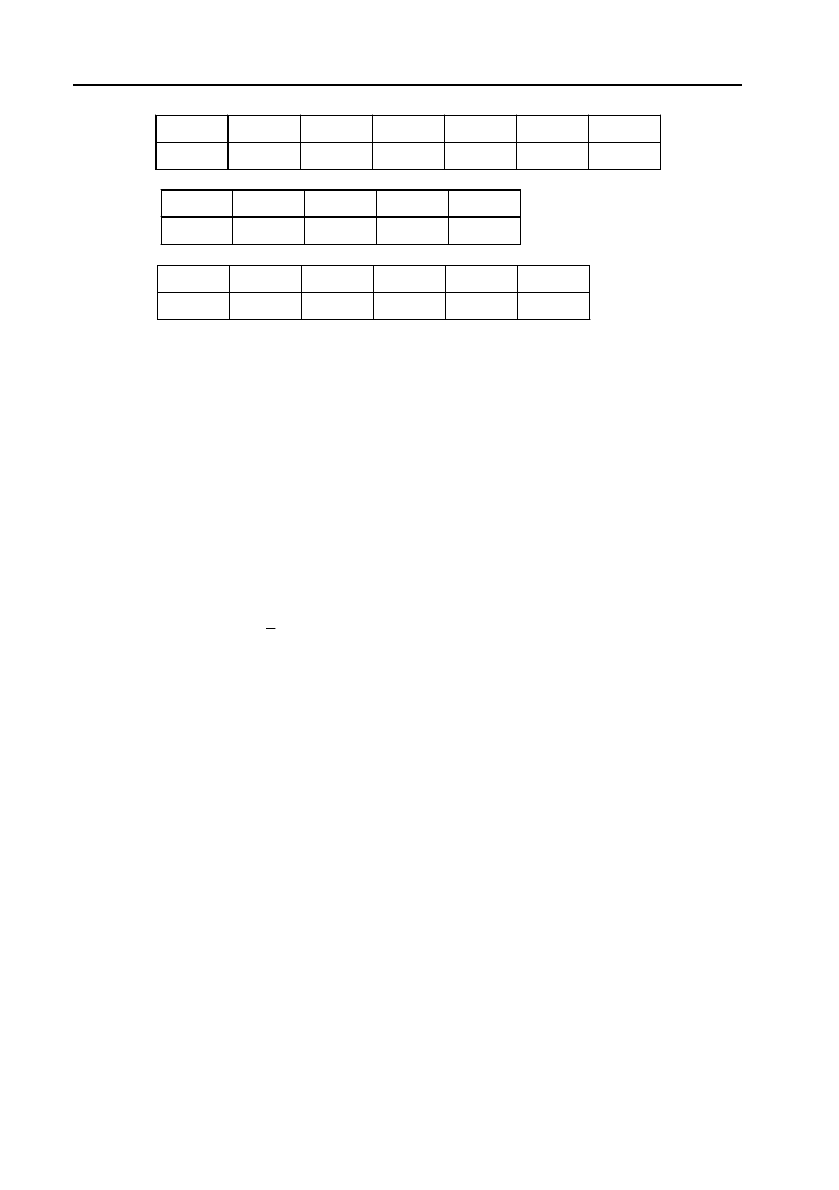
8. Методом най менших квадратів знайти рівняння прямої, що
проходить
через скупчення заданих точок:
x
2 3 5 6 9 12
a)
y
3 4 6 5 7 8
294
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Задачі з економічним змістом
9. Розв’язати задачі з використанням частинних похідних.
a)
Відкритий циліндр радіуса
r
та висотою
h
виготовлено із
матеріалу
вартістю 20 гривень за
2
.
м
Встановити можливу вартість
циліндра
V
як функцію
r
та
h
. З якою швидкістю змінюється
вартість
при зміні
r
або
h
?
b)
Закономірність втрати теплоти внаслідок конвекції має виг!
ляд
1
3
0
,
y
cT T V
де
T
– температура тіла,
0
T
– температура
зовнішнього
середовища,
V
– швидкість вітру,
c
– деяка стала.
Знайти:
0
,,,
TT V
y
yy
та вказати їх смисл.
c)
Задана функція попиту на товар
A
2
500 3 6 ,
A
BA
XPP
де
A
P
та
B
P
– вартість одиниці товарів
A
та
B
, відповідно. Визначити
еластичність
функції попиту відносно
A
P
та
B
P
, коли
5, 30.
AB
PP
d) Перевірити конкурентність товарів
A
та
B
, якщо функції
попиту
на ці товари
2
500 8 4 ;
A
BA
XPP
300 9 2
B
BA
X
PP
.
e)
Знайти маргінальну продуктивність праці та капіталу для про!
дуктивної функції
1
,
aa
P
cK x
де
c
та
a
– постійні.
x
3 4 5 6 7 8
b)
y
0,7 1,9 2,1 2,5 3,4 4,5
x
0 1 2 3
c)
y
1 1,5 2,5 3
x
2 3 4 5 6
d)
y
2 4 3,5 5 6,5

295
Частина 9. Функції кількох змінних
10. Розв’язати задачі оптимізації.
a)–b)
Мале підприємство виробляє товари
A
та
.
B
Загальні
щоденні
витрати
C
виробництва (у гривнях)
x
одиниць товару
A
та
y
одиниць товару
B
відомі:
a)
22
1500 7,5 15 0,3 0,3 0,2 ;Cxyxyxy
b)
22
250 4 7 0,2 0,1 .Cxyxy
Визначити кількість одиниць товарів
A
та
B
, яку треба вироб!
ляти, щоб загальні витрати підприємства були мінімальними.
c)
Використовуючи
x
одиниць праці та
y
одиниць капіталу
(тисяч гривень), підприємство виробляє продукцію, загальна вартість
V
якої (у тисячах гривень) має вигляд
22
40 50 3 2 1,5Vyxxyyx
.
Знайти кількість одиниць праці та капіталу, при яких підприєм!
ство має оптимальну загальну вартість продукції. Чому дорівнює
значення
оптимальної загальної вартості?
d)
Підприємство виготовляє два різних типи товарів собіварті!
стю
10
та
30
гривень. Річний попит на товари
1
x
та
2
x
відомий (у
тисячах
одиниць):
121
30 2 5
x
PP
;
212
100 2
x
PP
.
де
1
P
та
2
P
– ціна продажу товарів першого та другого типів, відповідно.
Визначити
1
P
та
2
P
, при яких підприємство одержить максималь!
ний прибуток. Знайти величину максимального річного прибутку.
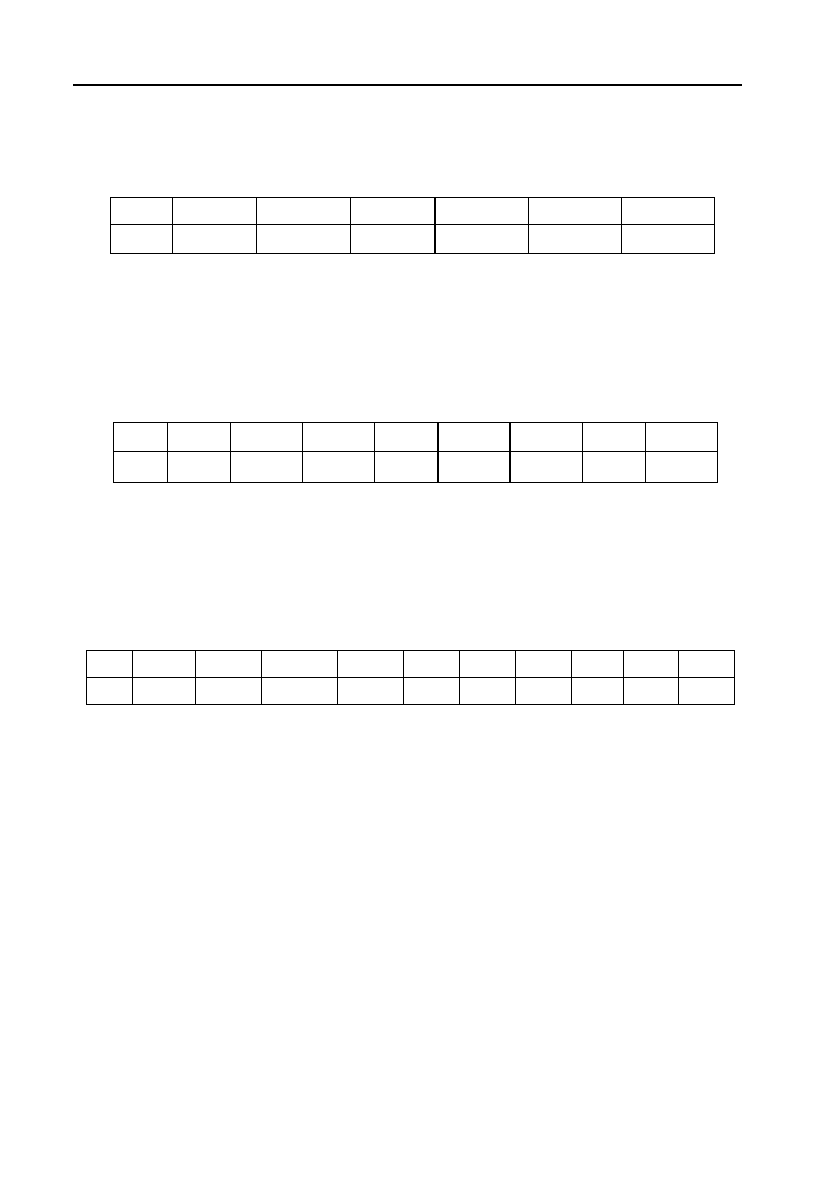
e)
При складанні телевізорів завод може використовувати кінес!
копи виготовлені в Кореї та Японії. Застосування кожного кінеско!
па із Кореї дає прибуток 5 гривень, а із Японії – 6 гривень.
Згідно з умовами постачання, кожного тижня завод може вико!
ристати
x
та
y
(тисяч) кінескопів, виготовлених в Кореї та Японії,
відповідно, причому
22
24560.xy xy
Знайти максималь!
ний щотижневий прибуток заводу і відповідний попит на кількість
кінескопів
з Кореї та Японії.
296
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
11. Розв’язати задачі з використанням методу найменших квад!
ратів.
a)
Таблицею задані величини товарного обігу
x
(тис. гривень).
Обрати вигляд залежності між
y
та
x
і визначити її параметри.
b)
В таблиці вказано кількість внесених добрив на 1 га
x
та
врожай
пшениці
y
центнерів.
Обрати вигляд залежності між
y
та
x
і визначити її параметри.
c)
Таблицею задані витрати пального на 100 км
y
в залежності
від
пробігу автомобіля
x
тис. км.
Обрати вигляд залежності між
x
та
y
і визначити параметри
цієї
залежності.
x
60
80
120
160
240
320
y
5510
5760
6235
6750
7685
8635
x
1
2
3
5
7
9
11 12
y
24
26,5
28
37
40
46
49
50,5
x
1 5 15 30 50 60 70 100 120 150
y
23,026 27,57 22,275 23,18 22,5 22,6 22,9 25 27,4 32,5

297
Частина 10. Інтегрування
Частина 10
ІНТЕГРУВАННЯ
10.1. Антипохідні (первісна та невизначений інтеграл)
10.1.1. Поняття антипохідних та інтегрування
Із
елементарної математики відомі взаємно обернені дії: додаван!
ня та віднімання, множення та ділення, піднесення до степеня та
добування
кореня, логарифмування та потенціювання. Іншою парою
взаємно
обернених математичних операцій є диференціювання та
інтегрування
.
У частині 8 викладено основи диференціального числення
функцій
однієї змінної. Диференціюванням функції, як відомо, на!
зивають процес знаходження похідної
F
x
або диференціала
dF x F x dx
заданої функції
F
x
.
Обернений процес – знаходження функції
F
x
за заданою по!
хідною
Fx
f
x
або заданим диференціалом
dF x
f
xdx
– називають інтегруванням функції
f
x
, а знайдену функцію
Fx
називають антипохідною або первісною.
Частину математики, що вивчає цей процес та його застосуван!
ня, називають інтегральним численням функції однієї змінної.
Розглянемо приклад задач, що приводять до необхідності інтег!
рування функції.
Якщо функція
St
вказує закон зміни відстані
S
з часом
t
нерівномірного руху, то миттєва швидкість цього руху
Vt S t
знаходиться диференціюванням функції
St
.

298
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Але іноді трапляється так, що швидкість нерівномірного руху
Vt
відома як функція часу
t
і треба знайти закон зміни
St
відстані
S
з часом
t
. У цьому випадку
St
задана і треба виз!
начити
St
, тобто виконати операцію, обернену диференціюван!
ню.
Інший приклад, якщо нам відома маргінальна функція витрат
Vx
і треба знайти функцію продуктивних витрат
Vx
вироб!
ництва
x
одиниць продукції.
Означення 1. Первісною функцією для заданої функції
f
x
називають таку функцію
,
F
x
похідна якої дорівнює
,
f
x
або диференціал якої дорівнює
fxdx
.
Отже, первісна функція
F
x
для заданої функції
f
x
задо!
вольняє рівності
Fx
f
x
або
dF x f x dx
.
Наприклад, функція
3
3
x
Fx
буде первісною для функції
2
f
xx
тому, що
3
2
3
x
x
або
3
2
3
x
dxdx
.
Згідно з правилами диференціювання, функції, що відрізняють!
ся лише постійним доданком, мають однакову похідну, тобто
F
xC Fx fx
.
Тому, якщо
fx
має первісну
F
x
, то вона має нескінченну
кількість
первісних функцій, відмінних одна від одної на постійний
доданок
, тобто функцій вигляду
F
xC
, де
C
– довільна стала.

299
Частина 10. Інтегрування
Наприклад, функція
2
3fx x
має первісні
33 3 3
,1,7,,xx x xC
тому, що похідні усіх ціх функцій однакові і дорівнюють
2
3x
.
Теорема 1. Будьякі дві первісні для заданої функції
fx
відрізняються лише постійним доданком.
Доведення
. Нехай
1
F
x
та
2
F
x
– первісні для функції
.fx
Тоді
12
F
xFx
f
x
.
Звідси випливає, що
12
0
Fx Fx
або
12
0.Fx Fx
Остання рівність означає, що
12
Fx Fx C
або
12
Fx Fx C
,
що і треба було довести.
Наслідок. Щоб знайти усю нескінченну множину первісних
функцій
(сукупність антипохілннх) достатньо знайти лише одну
первісну
функцію, а усі інші одержати додаванням до неї постійної.
Отже, сукупність первісних функцій має вигляд
,
F
xC
якщо
Fx
– одна із первісних.
Означення 2. Сукупність усіх первісних
F
xC
для заданої
функції
fx
називають невизначеним інтегралом і позначають
fxdx
. Отже.
fxdx Fx C
.
Знак
означає операцію інтегрування і називається знаком
інтеграла
, вираз
f
xdx
називають підінтегральним виразом,
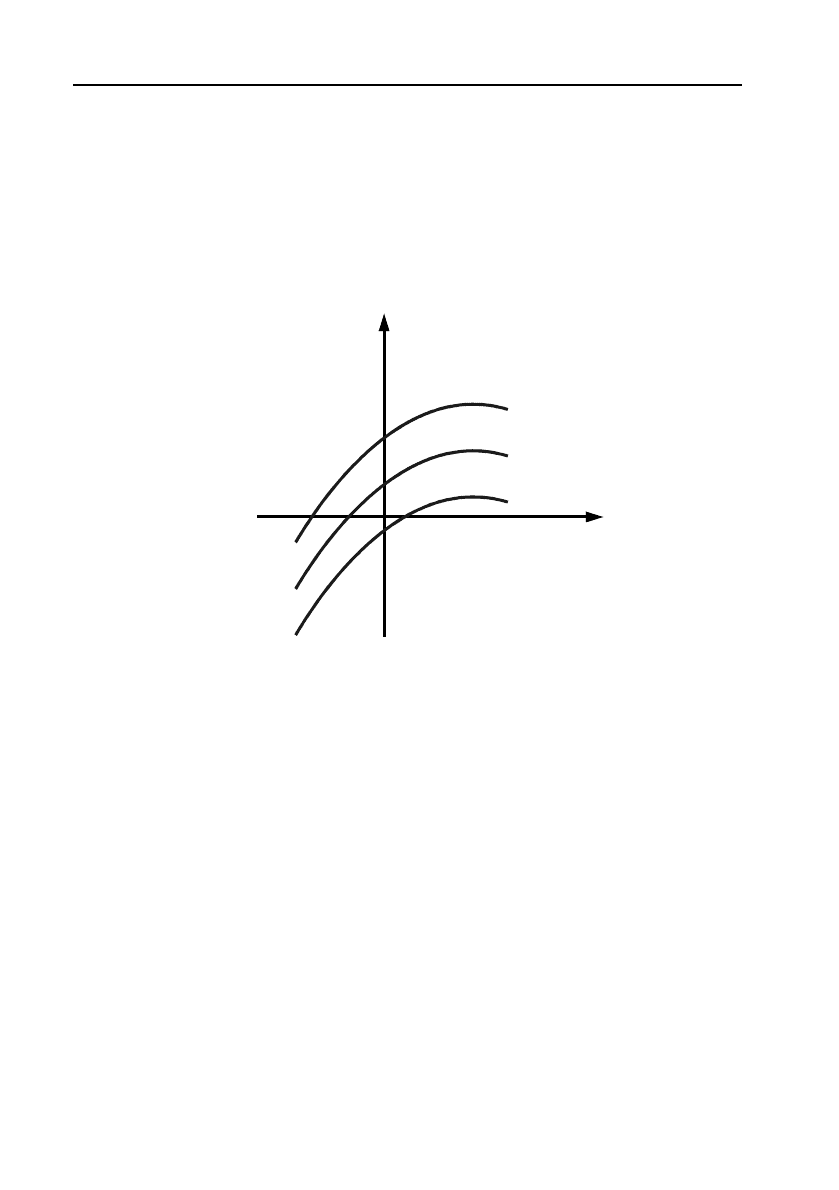
300
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
функцію
f
x
– підінтегральною, змінну
x
, що стоїть під знаком
диференціала
, називають змінною інтегрування,
F
x
– деяка пер
вісна для заданої
f
x
, а
C
– довільна постійна інтегрування.
Процес знаходження невизначеного інтеграла називають інтег
руванням
.
Якщо побудувати криву!графік однієї первісної функції
F
x
(мал. 1), то усі інші криві (графіки інших первісних для однієї
функції
) одержуються шляхом зміщення цієї кривої по
O
y
на вели!
чину, що дорівнює значенню постійної
C
.
10.1.2. Основні властивості невизначеного інтеграла
1. Диференціал невизначеного інтеграла дорівнює підінтегрально&
му виразу, тобто
d fxdx f xdx
.
Дійсно, за означенням невизначеного інтеграла маємо
,fxdx Fx C
де
Fx
f
x
.
Y
0
X
C
1
y = F(x)
y = F(x) + C
0
y = F(x) + C
1
Мал. 1.
