Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

301

Частина 10. Інтегрування

10.1.3. Таблиця основних інтегралів

Згідно

з означенням невизначеного інтеграла

якщо

 

dF u

udu



то

 

.fudu Fu C



Тому, використовуючи таблицю диференціалів основних елемен!

тарних функцій, одержимо таблицю інтегралів

dudu















,1;

udu C n



 







ln ,



ln ;





dadu









;

adu C







de edu

edu e C



;

Тому

    

dfxdx dFx C dFx Fxdx fxdx





 





Невизначений інтеграл від диференціала функції дорівнює сумі

функції

та довільної сталої, тобто

 

dF x F x C



Дійсно,

   

.dFx F xdx fxdx Fx C





 

Зауважимо, що з першої властивості випливає, що комбінація

символів

""d



, застосована до виразу



fxdx

, взаємно знищуєть!

ся. З другої властивості випливає, що комбінація символів

""d



застосована до деякої функції



, додає до цієї функції довіль!

ну сталу

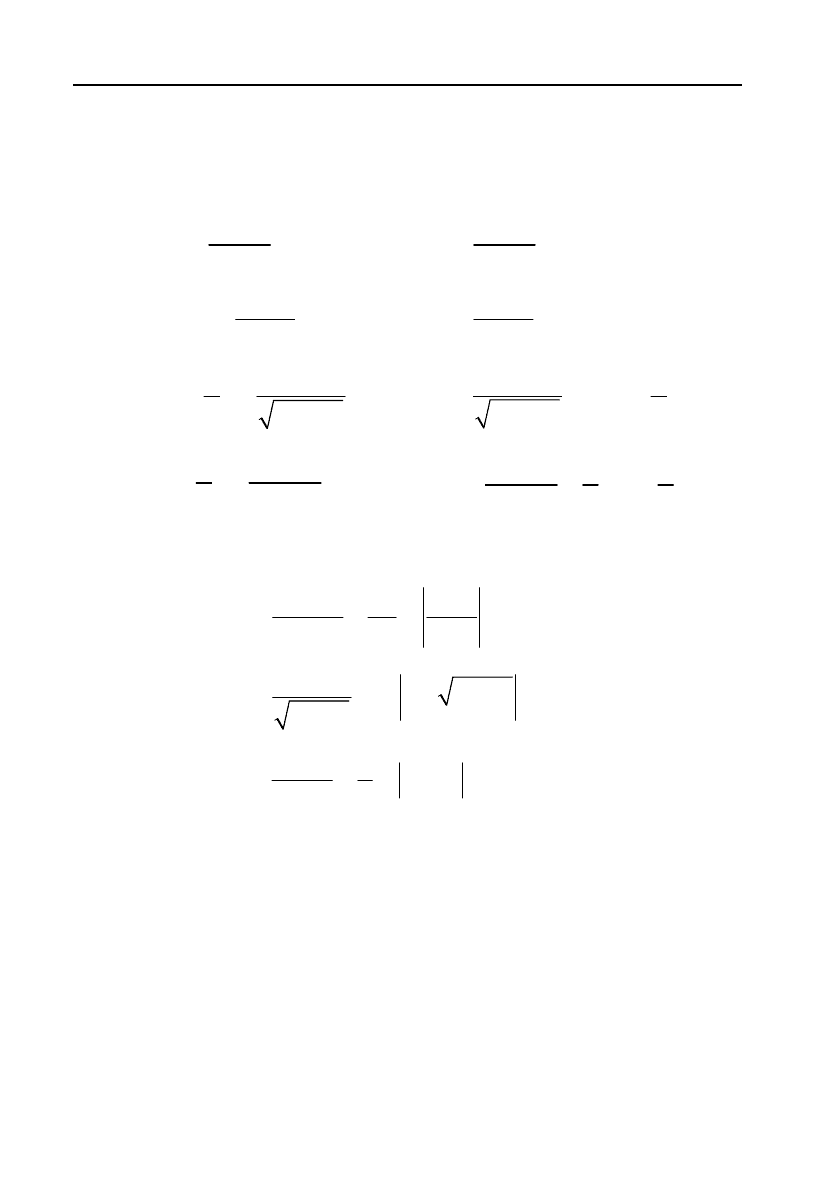
302

Барковський В.В., Барковська Н.В. «Вища математика для економістів»



sin cos ,

du udu



cos sin ;udu u C





cos sin ,

duudu



sin cos ;udu u C 





tg ,

cos



tg ;

cos







ctg ,

sin



ctg ;

sin

 



arcsin ,

udu











arcsin ;

du u







arctg ,

u adu











10.

arctg .

du u







Додамо до цієї таблиці ще три інтеграла, які часто використову!

ються.

11.

du u a

ua aua









12.

uuaC







13.

udu

uaC









У цих формулах

може бути незалежною змінною





або

проміжним

аргументом



.ux





Основні (табличні) інтеграли грають важливу роль в інтеграль!

ному численні, тому їх треба запам’ятати. Більш повна таблиця не!

визначених інтегралів наведена у таблиці в кінці підручника.

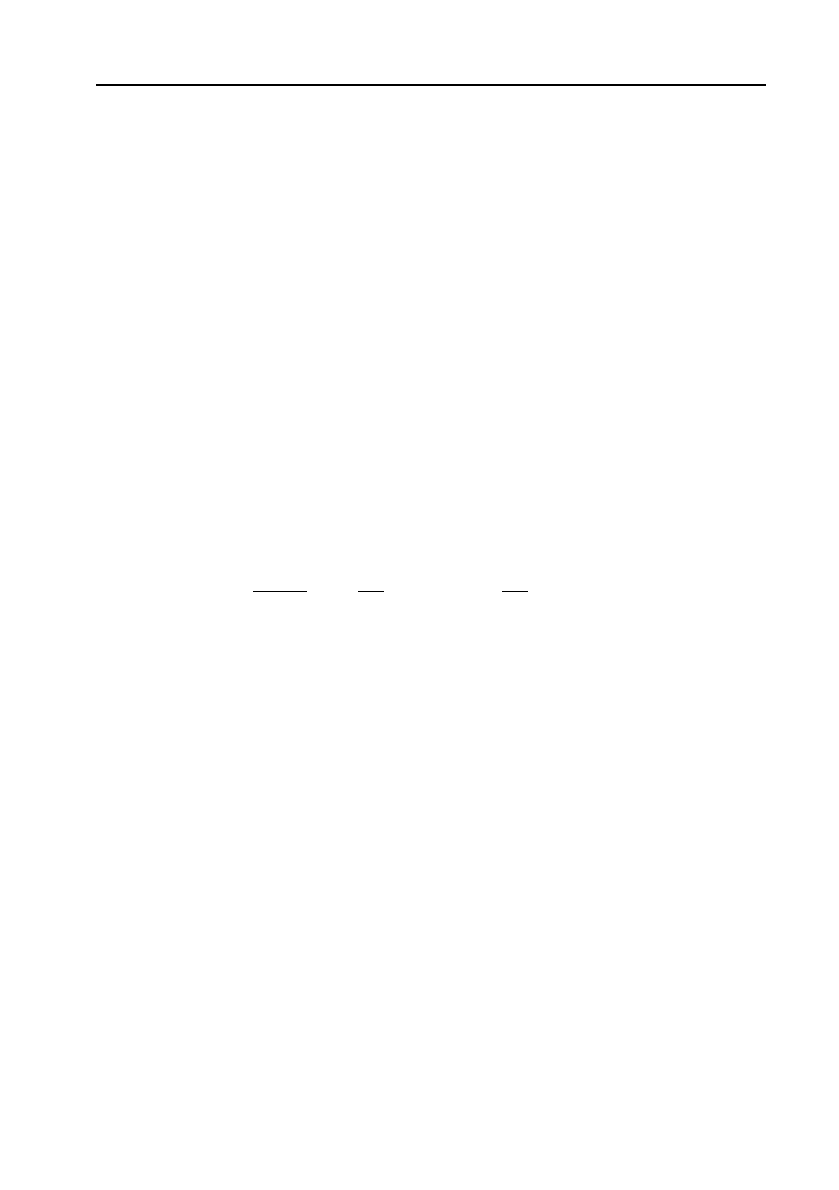
303

Частина 10. Інтегрування

10.1.4. Основні правила інтегрування

1. Постійний множник

можна виносити за знак інтеграла:

 

Afudu A udu



Дійсно, позначимо



Audu



тоді

  

dy d A f u du Ad f u du A f u du









Звідси одержуємо:



Af u du



Отже,

 

,Af u du A f u du



що і треба було довести.

Наприклад,

cos 1 1

cos sin .

12 12 12

dx xdx x C





2. Невизначений інтеграл від алгебраїчної суми скінченої кількості

функцій

дорівнює тій самій алгебраїчній сумі невизначених інтегралів

від

кожної із функцій&додатків:

     

12 1 2mm

f u f u f u du f u du f u du f u du



   







. (1)

Дійсно, позначимо

  

f u du f u du f u du

 



(2)

і знайдемо диференціал цієї функції

  

dy d f u du d f u du d f u du 







  

12 m

udu





Але тоді первісною буде

  

fu fu f u du















. (3)

304

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Ліві частини в (2) і (3) рівні, тому і праві частини також рівні,

тобто має місце рівність (1), яку треба було довести.

Зауважимо, що застосування цих правил в деяких випадках по!

требують певних перетворень.



Приклад 1.



21 4 41 4 4

44 .

xdx xxdxxdxxdxdx

   

  

 

b) Знайти антипохідні функцій



35 7

ttt

 





Розв’язання. Сукупність усіх антипохідних – це невизначений

інтеграл

. Згідно з правилами інтегрування та таблиці інтегралів одер!

жуємо:

35 7 3 5

7357

ttt dt

dt t dt t dt dt



 



 





 

tdt



21 11 2

3 5ln 7 5ln 7

12 2

tt t

tt C t t C

 

     





Приклад 2. Заданий маргінальний доход фірми



15 0,01





Знайти функцію доходу та визначити відношення між вартістю

одиниці

продукції та проданою її кількістю.



Розв’язання. Функцію доходу фірми можна знайти інтегруван!

ням маргінального доходу, тобто

   

15 0,01 15 0,01Dx D xdx xdx dx xdx





 

15 0,01 15 0,005

Cx xC  

305

Частина 10. Інтегрування

10.2. Методи інтегрування

Перш за все відмітимо, що в усіх табличних інтегралах підінтег!

ральна функція є певною функцією, аргумент якої співпадає із

змінною

інтегрування.

Розглянемо, наприклад, інтеграл



sin 1xdx



. В цьому випад!

ку аргументом основної елементарної функції синус буде



а змінна інтегрування –

, тому при знаходженні цього інтеграла не

можна

використати табличну формулу

sin cosudu u C 



Заданий невизначений інтеграл



xdx



можна знайти, якщо

якимось

чином вдається звести його до одного із табличних інтегралів.

Найбільш часто для знаходження заданого невизначеного інтег!

рала використовують методи: безпосереднього інтегрування, заміни

змінної

(підстановки), інтегрування частинами, а також знаходжен!

ня заданого інтеграла за допомогою довідника.

Ознайомимось з основними методами інтегрування.

де

– постійна інтегрування. Для знаходження

використаємо той

факт

, що доход повинен дорівнювати нулю, коли не продано жодної

одиниці

продукції, тобто при

0x 

маємо



01500,0050 0CC   

Отже, функція доходу фірми має вигляд



15 0,005

xx x



Якщо вартість кожної одиниці проданої фірмою продукції

продали

одиниць продукції, то доход буде



xPx



Отже, маємо

15 0,005 15 0,005Px x x P x





Остання рівність описує потрібне відношення.

306

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

10.2.1. Метод безпосереднього інтегрування

Цей

метод базується на рівності



,dx d ax b



де

та

сталі і застосовується у тих випадках, коли підінтегральна функція

заданого

інтеграла має вигляд однієї із підінтегральних функцій таб!

личних інтегралів, але її аргумент відрізняється від змінної інтегру!

вання постійним доданком або постійним множником або постійним

множником

та постійним доданком.



Приклад 3. Знайти інтеграли:

а)



dx



cos ;



с)



37 .xdx





Розв’язання.

 



81 9

333

81 9

xdxxdx C C





   





У цьому випадку змінна інтегрування

відрізняється від аргу!

менту степеневої функції



3ux

на постійний доданок 3;

cos cos 2sin

2222

xxxx

dx d C











У цьому випадку аргумент функції косинус відрізняється від

змінної

інтегрування

на множник





(37) 37 37

xdx x dx C





   







xC

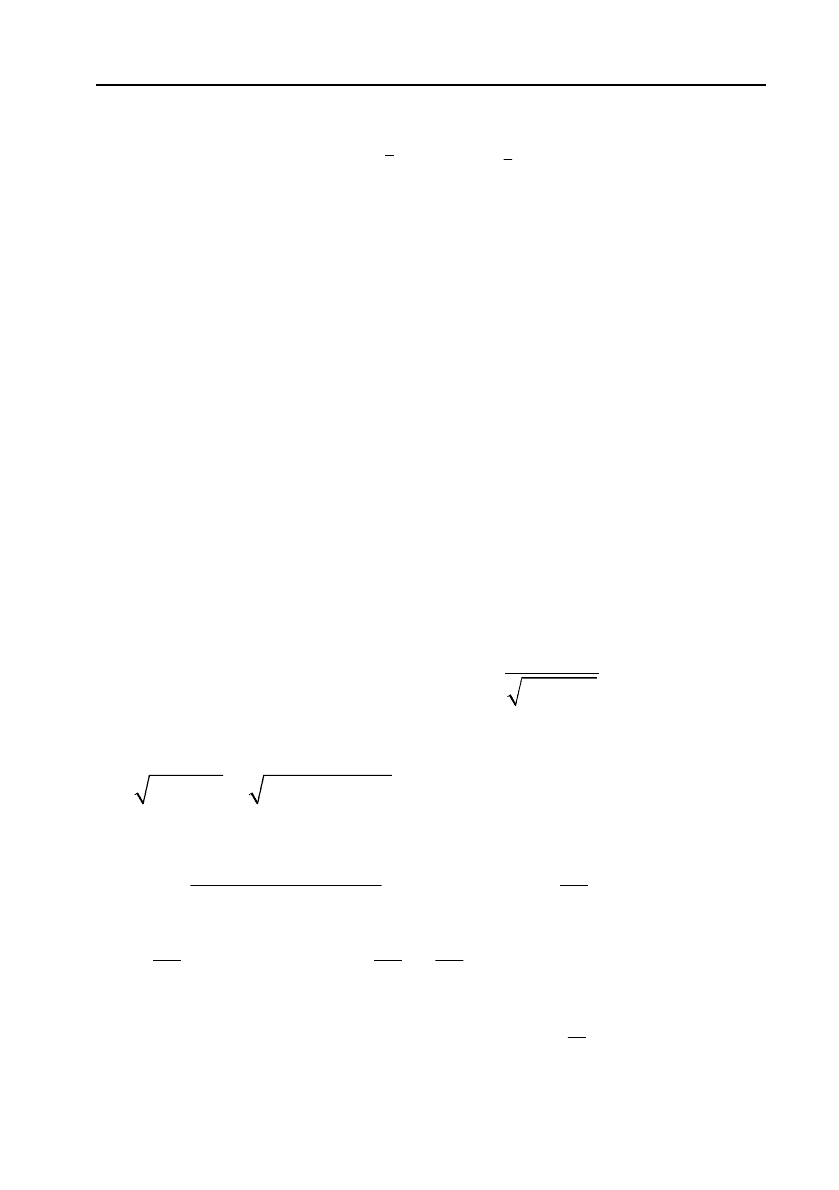
307

Частина 10. Інтегрування

10.2.2. Метод підстановки (заміни змінної)

Цей

метод містить два прийоми.

а) Якщо для знаходження заданого інтеграла



xdx



зробити

підстановку



,xt





тоді має місце рівність

   

xdx f t tdt













Після знаходження останнього інтеграла треба повернутись до

початкової

змінної інтегрування

. Для застосування цього прийо!

му треба, щоб функція







мала обернену



.tx







Приклад 4. Знайти інтеграл

xdx









Розв’язання. Зробимо підстановку

5sinxt

, тоді

25 25 25sin 5cos ,

  



5sin 5cosdx t dt t dt





Отже, одержимо



25sin 5cos 25

25 sin 1 cos 2

5cos 2

ttdt

Jtdttdt









25 25 25

cos2 sin 2

224

dt tdt t t C  



Із рівності

5sinxt

одержимо

arcsin









;

У цьому випадку змінна інтегрування

відрізняється від ар!

гумента степеневої функції



37ux

постійним множником 3

та постійним доданком



7.

308

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

sin 2 2sin cos 2 25

ttt x

Отже,

25 25 2

arcsin 25

25425

JxC

arcsin 25

252

xC 

Якщо зробити заміну змінної, тобто







тоді має місце

рівність

  

x x dx f t dt













Після знаходження останнього інтеграла треба повернутись до

змінної

, використовуючи рівність









Приклад 5. Знайти

xdx





Розв’язання.

Нехай

t

тоді

33,

tx t





2.dx tdt

Тому

  

242

33223xx dx t t tdt t tdt  

 

4253

tdt tdt t t C



 

32 3

xxC

 



Зауваження:

1. Якщо підстановка обрана вдало, то одержаний інтеграл буде

простішим

і мета підстановки досягнута.

Якщо підінтегральний вираз містить корінь вигляду



то доцільно застосувати тригонометричну підстановку

cosxa t

або

sinxa t

Знаходження вдалої підстановки для інтегрування певної мно&

жини функцій є значною подією в інтегральному численні. Видатний

309

Частина 10. Інтегрування

10.2.3. Метод інтегрування частинами

Цей

метод застосовується тоді, коли під інтегралом є добуток

функцій

, причому хоча б одна з них є трансцендентною (не степене!

вою).

Нехай

та

деякі функції

, тобто



uux





vvx



Розглянемо диференціал добутку цих функцій:



duv udv vdu

Інтегруючи обидві частини рівності, одержимо



duv udv vdu  





Звідси, враховуючи властивість невизначеного інтеграла, маємо

.uv udv vdu   



Отже, одержали формулу

,udv uv vdu



(4)

яку називають формулою інтегрування частинами.

вчений ХVІІІ ст., член Петербурзької академії наук Л.Ейлер вказав

підстановку

tx x a 

для знаходження інтеграла

a



У цьому випадку

222

xdxdt

dt dx

axaxxa















або

dx dt





Отже,

ln ln

dx dt

tC x x aC







310

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Ця формула дозволяє знаходження інтеграла

udv



звести до

знаходження

інтеграла

.vdu



При вдалому обранні

та

інтег!

рал може бути табличним або простішим ніж заданий інтеграл

.udv





Приклад 6. Знайти

ln xdx





Розв’язання. Нехай

ln ,



.dv dx

Тоді



vx

За формулою інтегрування частинами (4) одержимо

ln ln ln ln

xdx x x x x x dx x x x C

     



Рекомендація до застосування методу інтегрування частинами

При

обранні



та



dv x

слід пам’ятати, що спрощення зада!

ного інтеграла можливе за рахунок диференціювання функції



В інтегралах вигляду



;

Px edx





sin ;

xxdx





cos

xxdx



(



– багаточлен)

доцільно обирати



uPx

, а залишену частину підінтегрального ви!

разу позначати

В інтегралах вигляду



ln ,Px xdx





arctg ,

xxdx





arcsin .

xxdx



доцільно брати



,dv P x dx

а залишок підінтегрального виразу до!

рівнювати