Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.

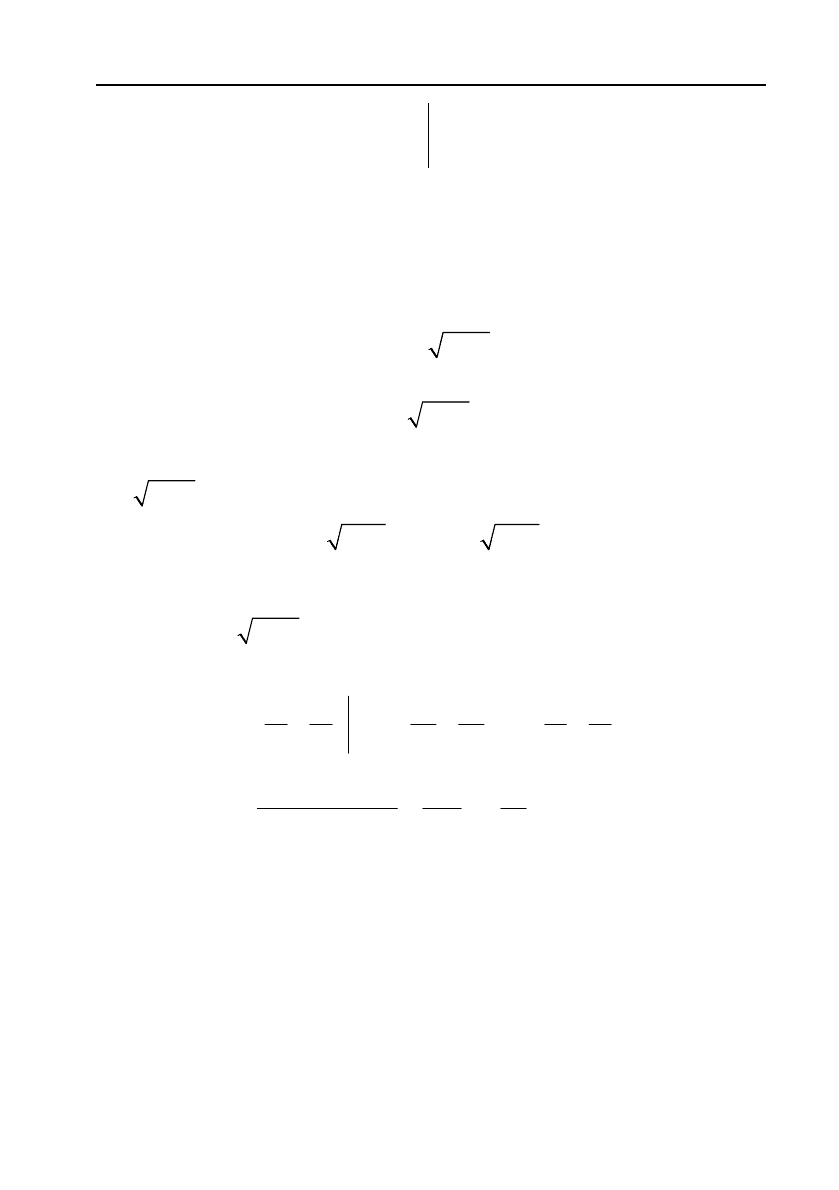
331
Частина 11. Визначені та невласні інтеграли
ft tdtFt F F
b
a
Fb Fa fxdx
.
що й треба було довести.
Приклад 3. Обчислити
3
0
1xxdx
.
Розв’язання. Нехай
1
tx
, тоді
22
11
txxt
,
2
dx tdt
. Знайдемо межі інтегрування, використовуючи рівність
1
tx
:
10 1; 13 2.
HB
tt
Отже,
32 2
22 42
01 0
1122x xdx t t dt t t dt
53 5 3 53
2
1
22 11
222
53 53 53
tt
964035 116 11
27
15 15 15
.
11.2.4. Методи наближеного обчислення
Для
деяких неперервних підінтегральних функцій
f
x
первіс!
ну не можна виразити елементарними функціями. У цих випадках
обчислення
визначеного інтеграла за формулою Ньютона!Лейбніца
неможливе
.
Крім того, у практичній діяльності часто досить знати лише на!
ближене значення визначеного інтеграла і знаходити це наближене

332
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
значення такими методами, які дозволяють використовувати сучас!
ну обчислювальну техніку.
Тому математики багатьох країн розробляють ефективні методи
наближеного
обчислення визначеного інтеграла.
Найбільш часто використовують три методи: метод прямокут!
ників, метод трапецій та метод парабол (метод Сімпсона).
Якщо відрізок інтегрування
,
ab
поділити на
n
рівних частин
довжиною
ba
x
n
і позначити через
k
середню точку відрізку
1
,,
kk
xx
тоді визначений інтеграл можна обчислити за формулою
12
,
b
n
a
ba
fxdx f f f
n
(10)
яку називають формулою прямокутників. Чим більше буде
n
тим
менший
буде крок
ba
x
n
і права частина (10) буде давати більш
точне
значення інтеграла.
Якщо поділити відрізок інтегрування точками ділення
012 1
nn
ax x x x x b
на
n
рівних частин довжиною
ba
x
n
і позначити значення функції
в
точках ділення
k
f
x
, тоді визначений інтеграл можна обчислити за
формулою
1
1
2
b
n
k
k
a
fa fb
ba
f
xdx fx
n
, (11)
яку називають формулою трапецій. Легко бачити, що при зростанні
n
крок
ba
x
n
зменшується, тому значення інтеграла буде більш
точним
.

333
Частина 11. Визначені та невласні інтеграли
Якщо відрізок інтегрування
,ab поділити на парну кількість
рівних
частин (тобто
2nm
) і позначити
kk
yf
x
, де
k
x
axk
— точки ділення,
0, 1, ,2km
, тоді визначений
інтеграл
можна обчислити за формулою
02 24 22
13 21
2
2
4
b
mm
a
m
yy yy y
ba
fxdx
m
yy y
, (12)
яку називають формулою Сімпсона. Ця формула дає більш точне зна!
чення визначеного інтеграла тому, що для її доведення використовуєть!
ся метод парабол, за яким на кожному відрізку
1
,
kk
xx
три значення
функції
fx
входять до інтегральної суми.
11.3. Невласні інтеграли
11.3.1. Поняття та різновиди невласних інтегралів
Згідно
з теоремою існування визначеного інтеграла цей інтеграл
існує
, якщо виконані умови:
1)
відрізок інтегрування
,
ab
скінченний;
2)
підінтегральна функція
f
x
неперервна або обмежена і має
скінченну
кількість точок розриву. Якщо хоча б одна із умов не ви!
конується, то визначений інтеграл називають невласним.
Якщо не виконується перша умова, тобто
b
або
a
або
a
та
b
, то інтеграли називають невласними інтегралами
з нескінченними межами
.
Якщо не виконується лише друга умова, то підінтегральна фун!
кція
fx
має точки розриву другого роду на відрізку інтегрування

334
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
,ab
. В цьому випадку
b
a
fxdx
називають невласним інтегра
лом від розривної функції або від функції, необмеженої в точках
відрізку інтегрування.
11.3.2. Дослідження невласних інтегралів
Дослідження
невласних інтегралів проводять шляхом викорис!
тання граничного переходу до визначеного інтеграла.
Інтеграли з необмеженими межами розглядають так:
lim ;
b
b
aa
f
xdx f xdx
lim ;
bb
a
a
f
xdx
f
xdx
lim lim
ccb
ab
cac
f
xdx fxdx fxdx fxdx fxdx
.
Якщо вказані границі існують (будуть скінченними числами), то
відповідний
інтеграл називають збіжним і він дорівнює своїй гра!
ниці.
Якщо якась границя не існує або дорівнює нескінченності, то
інтеграл
називають розбіжним.
Приклад 4. Обчислити інтеграл
2
1
dx
x
або встановити його
розбіжність
.
Розв’язання. Згідно з означенням невласного інтеграла, маємо
22
11
1
11
lim lim lim 1 1
b
bb b
b
dx dx
xb
xx
.
Отже, цей інтеграл існує, збіжний і дорівнює 1.
У випадку необмеженої на
,
ab
функції
f
x
її точки розриву
можуть
бути на лівому кінці або на правому кінці або всередині

335
Частина 11. Визначені та невласні інтеграли
проміжку інтегрування
,
ab
. У цих випадках невласні інтеграли
визначають
так:
0
lim ;
b
b
aa
f
xdx f xdx
0
lim ;
bb
aa
fxdx fxdx
00
lim lim
c
bb
aac
fxdx fxdx fxdx
.
Якщо вказані границі існують, то відповідний інтеграл нази!
вають збіжним. У протилежному випадку інтеграл називають роз
біжним
.
Приклад 5. Обчислити інтеграл
2
2
1
2
dx
x
або встановити його
розбіжність
.
Розв’язання. В точці
0x
підінтегральна функція необмеже!
на, тобто вона має розрив всередині проміжку інтегрування. За озна!
ченням такого невласного інтеграла маємо
22
222
00 0 0
11
2
1
11 11
lim lim lim lim
22
222
dx dx dx
xx
xxx
00 00
11111111111
lim 1 lim lim lim
2222242
.
Отже, інтеграл розбіжний.

336
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
11.4. Застосування визначених інтегралів
11.4.1. Обчислення площ
Якщо
на відрізку
,ab
функція
0fx
, то згідно з формулою
(4), обчислення площі криволінійної трапеції, зображеної на мал. 1,
можна знайти за формулою
b
a
Sfxdx
.
Якщо на відрізку
,
ab
функція
0
fx
, то криволінійна тра!
пеція, обмежена кривою
f
x
, відрізком
,
ab
та прямими
x
a
і
x
b
, буде розташована нижче осі
Ox
. Визначений інтеграл
b
a
f
xdx
у цьому випадку буде
0
. Але площа є невід’ємною ве!
личиною, тому площу криволінійної трапеції, розташованої нижче
осі
Ox
, треба знаходити за формулою
b
a
Sfxdx
або
b
a
Sfxdx
,
0
fx
.
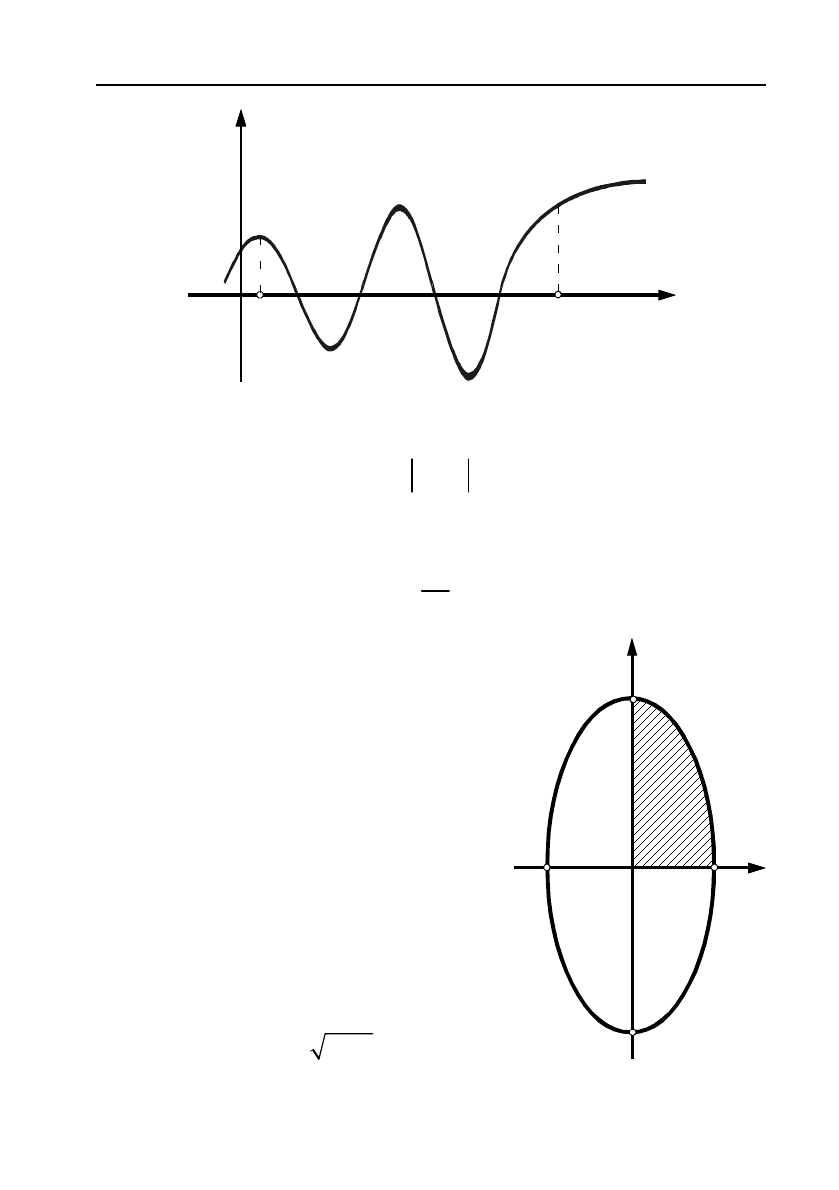
Якщо
f
x
на відрізку
,ab
декілька разів змінює свій знак, то
інтеграл
по відрізку
,
ab
треба розбити на суму інтегралів по част!
кових відрізках. Інтеграл буде додатним на тих відрізках, де
0fx
та від’ємним там, де
0
fx
. Інтеграл по відрізку
,
ab
дає різни!
цю площ, що лежать вище та нижче осі
Ox
(див. мал. 2).
Щоб одержати суму площ (без врахування розташування віднос!
но осі
Ox
) треба знайти суму абсолютних величин інтегралів по
часткових
відрізках або обчислити інтеграл від абсолютного значен!
ня функції тобто
337
Частина 11. Визначені та невласні інтеграли
b
a
Sfxdx
.
Приклад 6. Обчислити площу фігури, обмеженої еліпсом
2
2
1
4
y
x
.
Розв’язання. Із аналітичної гео!
метрії відомо, що цей еліпс має вигляд
такий
, як на мал. 3.
Шукана площа
S
дорівнює
1
4
S
, де
1
S
– площа заштрихованої частини еліп!
са, що розташована у першому квадранті
Отже
,
1
0
4Sydx
.
Із рівняння еліпса знаходимо
y
:
22
41
yx
21
y
x
.
Мал. 2.
y = f(x)
0
X
+
Y
a
b
++
––
Мал. 3.
2
0
X
Y
–2
1
–1
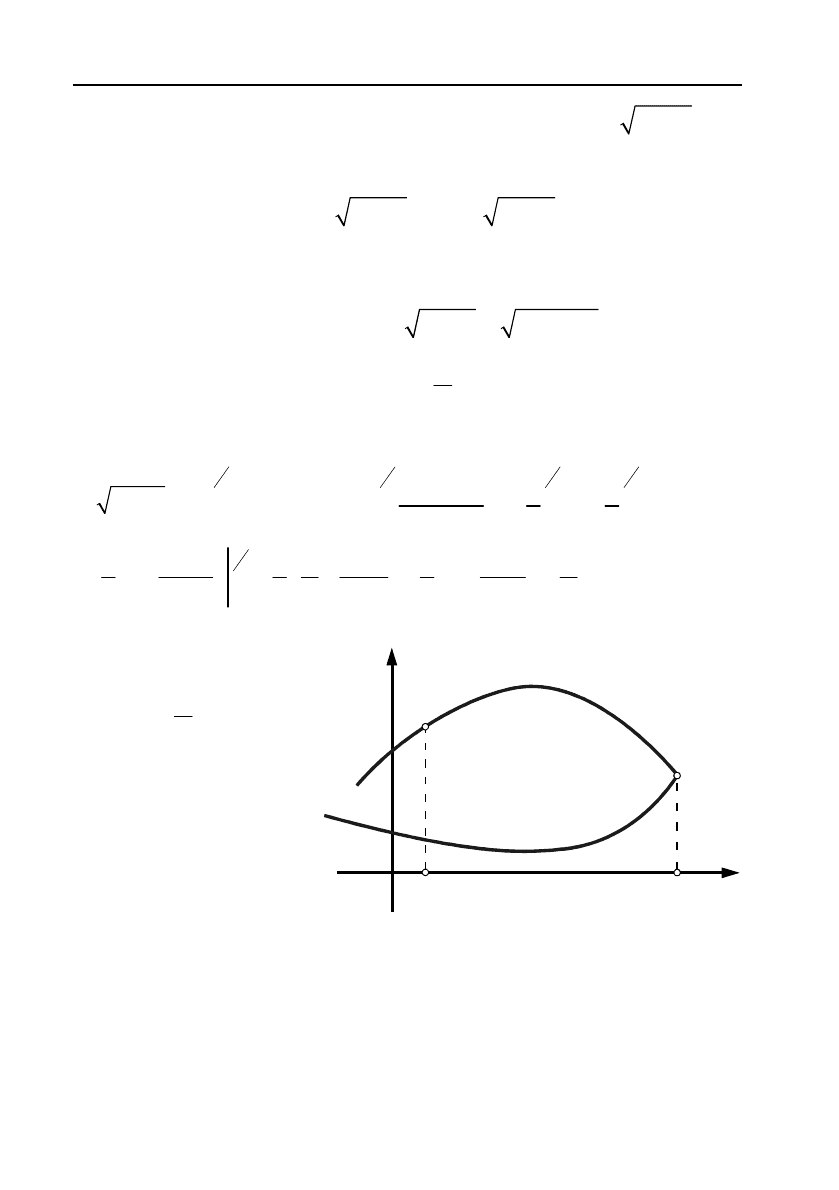
338
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Для заштрихованої частини еліпса
0
y
, тому
2
21
y
x
і ми
одержуємо
11
22
00
421 8 1Sxdxxdx
. (13)
Заміна
sin
x
t
дає:
cosdx t dt
;
arcsintx
,
22
11sincosxtt
;
arcsin0 0
H
t
;
arcsin1
2
B
t
.
Отже,
1
2222
2
00 0 00
2
0
1cos2 1 1
1 cos cos cos2
222
1 sin2 1 sin 1 sin0
0.
22 222224
t
xdx t tdt dt dt tdt
t
t
За формулою (13)
одержимо
82
4
S
(квадратних одиниць).
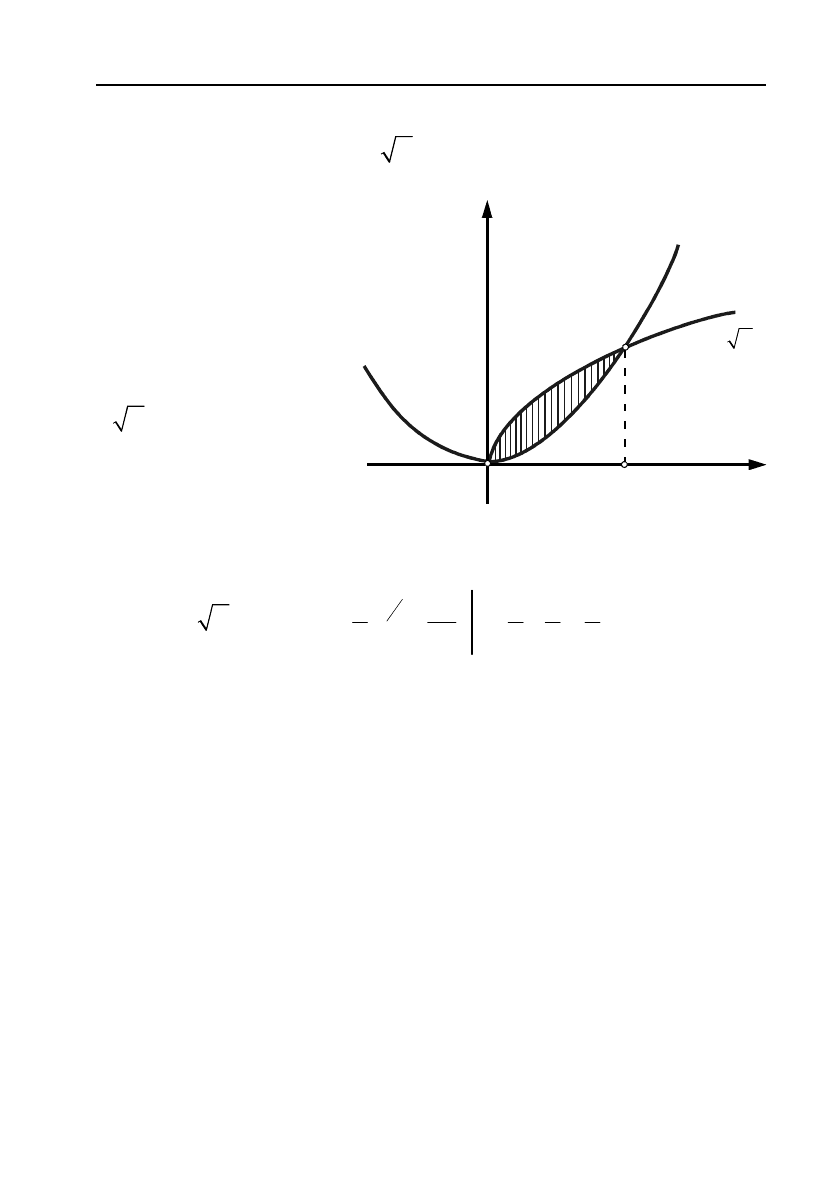
Якщо треба обчис!
лити площу фігури,
обмеженої кривими
1
yf
x
,
2
yf
x
та
прямими
x
a
,
x
b
(дивись, наприклад, мал.
4),
то при
12
fx fx
її можна знайти за формулою
12
b
a
Sfxfxdx
. (14)
Мал. 4.
0
X
Y
a
b
y = f
2
(x)
y = f
1
(x)
339
Частина 11. Визначені та невласні інтеграли
Приклад 7. Обчислити площу фігури, обмеженої лініями
y
x
та
2
y
x
.
Розв’язання. Спо!
чатку зобразимо фігуру,
площу якої треба знайти
(мал. 5). Знайдемо точку
перетину
цих парабол.
Координати точок пере!
тину задовольняють
обом
рівнянням, тому
24
xx xx
4
0xx
12
0, 1xx
.
Отже, площа заштрихованої фігури буде
1
3
3
2
2
0
1
0
2211
33333
x
Sxxdxx
(квад. одиниць).
Мал. 5.
0
X
Y
1
y = x
2
y
x
11.4.2. Обчислення довжини дуги кривої
Нехай
крива на площині має рівняння
y
fx
. Треба знайти
довжину
дуги
AB
цієї кривої, обмежену прямими
x
a
та
x
b
(див. мал. 6).
Візьмемо на
AB
точки
12 1
,,,, ,
n
AM M M B
з абсцисами
12 1
,,,, ,
n
ax x x b
відповідно, та проведемо хорди
112 1 1
,,, ,,
kk n
AM M M M M M B
,
довжини яких позначимо
12
,,,
n
ll l
.
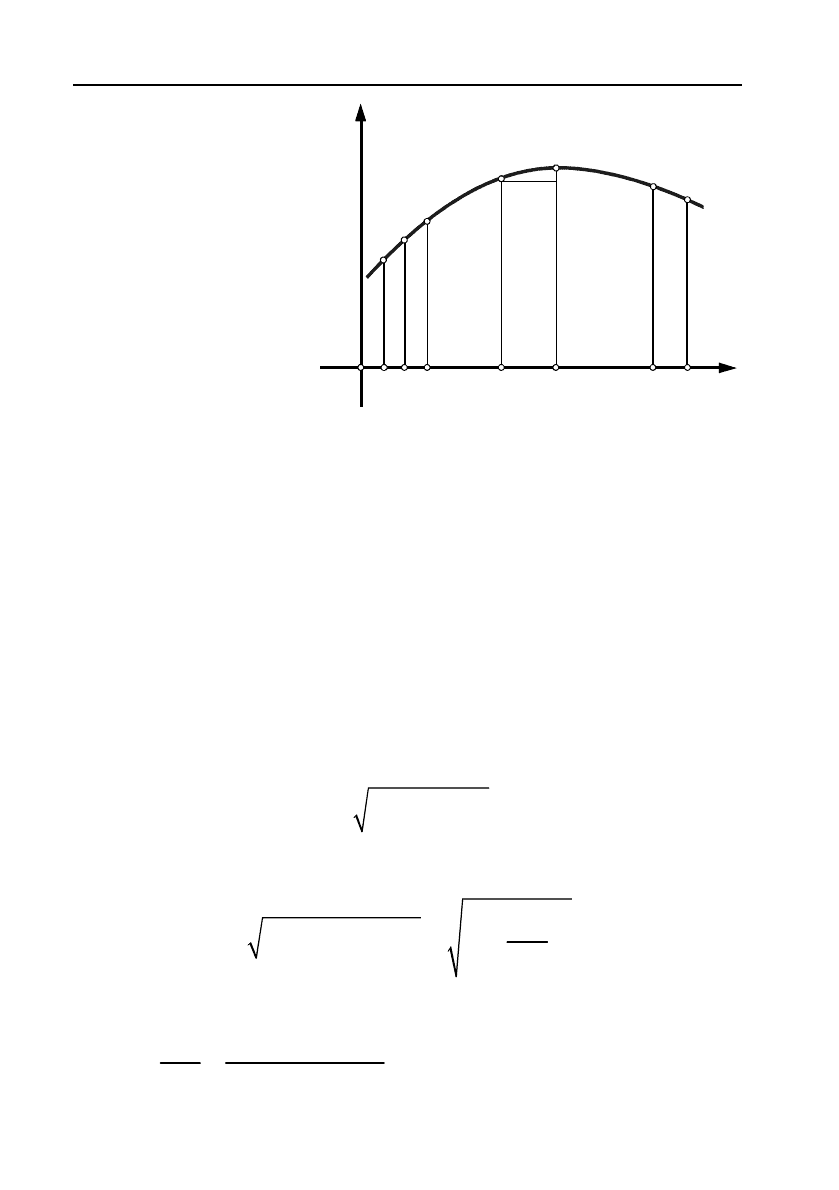
340
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Одержимо ламану
лінію
, вписану в дугу
AB
. Довжиною лама!
ної буде
1
n
nk
k
ll
.
Означення 3. Довжиною l дуги
AB
називають границю, до
якої
прямує довжина вписаної ламаної, коли довжина її найбільшої ча&
стини прямує до нуля, тобто
0
1
lim
k
n
k
max l
k
ll
.
Теорема 5. Якщо на відрізку
,ab
функція
fx та її по
хідна
f
x
неперервні, то довжина дуги кривої
yf
x
, обме
женої прямими
x
a
та
x
b
, обчислюється за формулою
2
1
b
a
l
f
xdx
. (15)
Доведення
. Із малюнка 6 бачимо, що за теоремою Піфагора
2
22
1
k
kkk k
k
y
lxy x
x
.
Згідно з теоремою Лагранжа маємо:
1
1
,
kk
k
k
kkk
fx fx
y
f
xxx
де
1
kkk
x
x
.
Мал. 6.
0
X
Y
a=x
0
x
n
=b
x
n–1
x
k
x
k–1
x
1
x
2
A
M
1
M
2
M
k–1
M
k
M
n–1
B
y = f(x)
dS
k
k
x
k
y
