Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.

101
Частина 4. Матриці та визначники
Приклад 3. Знайти обернену матрицю до матриці
12 3
25 7
3710
A
.
Розв’язання. Задана матриця А квадратна порядку 3, її визнач!
ник:
12 3
2 5 7 1510 273 273 335 2210 771 0
3710
A
.
Отже, ця матриця оберненої не має.
Зауваження. Якщо матриця А квадратна другого порядку
11 12
21 22
aa
A
aa
, визначник якої |А|
0, то обернену до неї матрицю
А
–1
можна знайти за формулою
22 12
1
21 11
1
,
aa
A
aa
A
(3)
тобто треба елементи головної діагоналі матриці А поміняти місцями,
елементи неголовної діагоналі помножити на (–1) і одержану матрицю
помножити на
1
A
.
Приклад 4. Знайти обернену матрицю до матриці
21
46
.
Розв’язання. Задана квадратна матриця другого порядку, її виз!
начник
21
26 41 12 4 8 0
46
.
том у для зн ах о д ж ен н я
А
–1
можна застосувати формулу (3).
102
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Одержимо:
1
61
1
8
42
A
.
Приклад 5. (Модель міжгалузевого планування потреб та
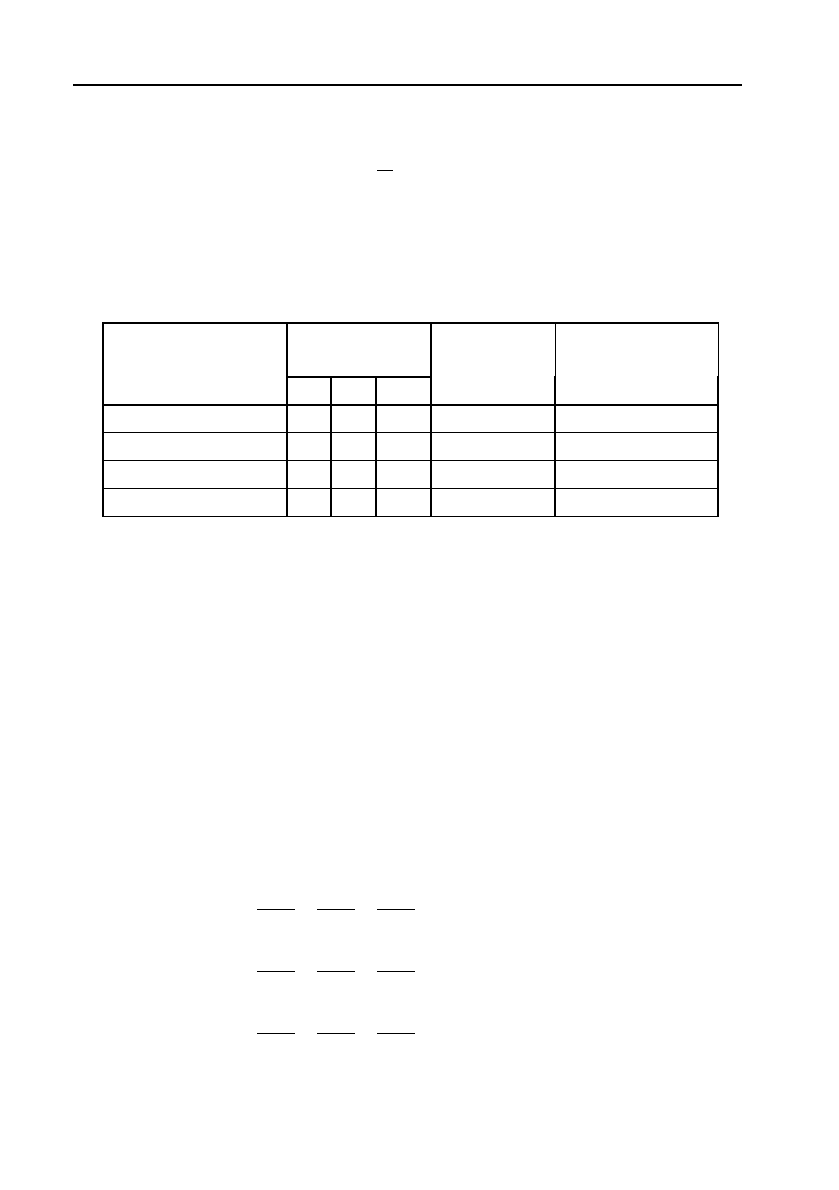
пропозицій). Таблицею задані показники взаємних потреб та пропо!
зицій між різними галузями промисловості.
a) Визначити матрицю потреб!пропозицій А.
b) Припустимо, що через три роки потреби інших галузей зрос!
туть до 24, 33 та 75 показників для галузей 1, 2, 3, відповідно. Скільки
продукції повинна виробити кожна галузь, щоб задовольнити ці по!
треби?
Розв’язання.
а) Елементи шуканої матриці А дорівнюють відношенню потреб
і!тої галузі до загальної кількості пропозицій цієї галузі. Тому для
знаходження елементів і!го стовпця (і = 1, 2, 3) матриці А треба
поділити потреби і!тої галузі, вказані у таблиці, на загальну кількість
пропозицій цієї галузі.
Таким чином, ми одержуємо матрицю потреб!пропозицій вигляду
20 48 18
100 120 180
0,2 0,4 0,1
30 12 54
0,3 0,1 0,3
100 120 180
0,3 0,3 0,2
30 36 36
100 120 180
A
.
Галузеві
потреби
Галузеві
пропозиції
1 2 3
Потреби
інших
галузей
Кількість
усіх
пропозицій
1 20 48 18 14 100
2 30 12 54 24 120
3 30 36 36 72 180
Витрати праці 20 24 72

103
Частина 4. Матриці та визначники
b) Нехай Е!одинична матриця третього порядку. Позначимо:
24
33
75
D
– матриця!стовпець нових потреб,
X – матриця нових пропозицій, що відповідають новим потре!
бам:
1 0 0 0,2 0,4 0,1 0,8 0,4 0,1
0 1 0 0,3 0,1 0,3 0,3 0,9 0,3
0 0 1 0,3 0,3 0,2 0,3 0,3 0,8
BEA
.
Тоді
1
X
BD
. (4)
Для обчислення майбутніх пропозицій залишилось знайти В
–1
.
Матриця В квадратна третього порядку, її визначник
0,8 0,4 0,1
0,3 0,9 0,3 0,336
0,3 0,3 0,8
B
.
Для знаходження матриці В
–1
, яка існує, знайдемо алгебраїчні
доповнення елементів матриці В: В
11
= 0,63; В
12
= 0,33; В
13
= 0,36;
В
21
= 0,35; В
22
= 0,61; В
23
= 0,36; В
31
= 0,21; В
32
= 0,27; В
33
= 0,6.
Отже, обернена матриця В
–1
має вигляд
1
0,63 0,35 0,21
1
0,33 0,61 0,27
0,336
0,36 0,36 0,6
B
.
Підставимо D та знайдену В
–1
у формулу (4), одержуємо
0,63 0,35 0,21 24 126,25
1
0,33 0,61 0,27 33 143,75
0,336
0,36 0,36 0,6 75 195
X
.

104
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Вправи до розділу 4.4
1. Знайти ранг матриці:
a)
235 7
462 3;
2 3 11 15
b)
21 1 3
40 1 7;
02 31
c)
110
201;
111
d)
1135
21 14
2263
; e)
12 1 3
3631
36 310
; f)
432
864
432
432
864
.
2. Знайти обернену матрицю до заданої матриці:
a)
12 1
21 3;
31 1
b)
111
10 2;
21 1
c)
123
456;
312
d)
32
;
11
e)
102
021;
210
f)
210
305;
764
g)
123
456.
789
3. Таблицею задані показники потреб!пропозицій трьох галузей
промисловості (N – номер варіанта):
Таким чином, через три роки першій галузі треба виробити 126,25
одиниць продукції, другій галузі потрібно виробити 143,75 одиниць
продукції, а третій галузі треба виробити 195 одиниць продукції .
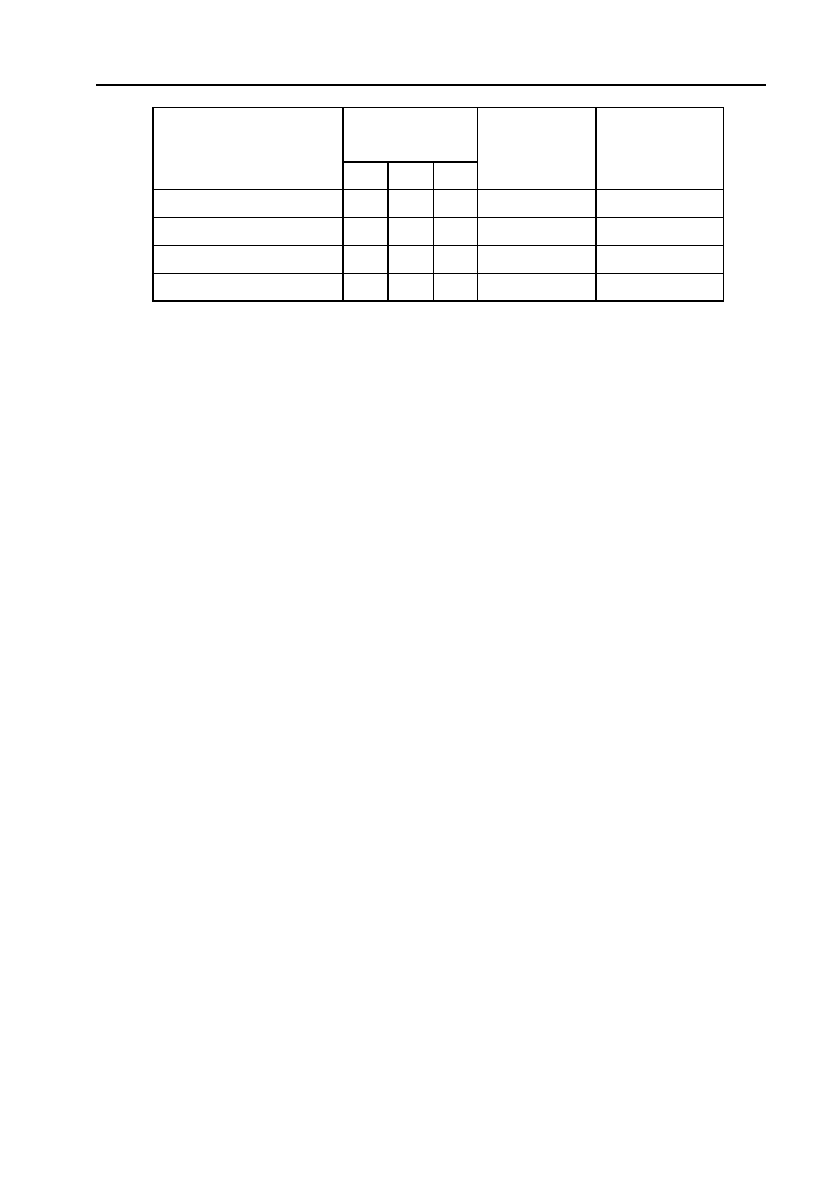
105
Частина 4. Матриці та визначники
4.5. Питання для самоперевірки
1. Дати означення матриці та її розміру. Які існують різновиди
матриць?
2. Які елементи утворюють головну та неголовну діагоналі мат!
риці?
3. За якими правилами матрицю помножають на дійсне число,
знаходять алгебраїчну суму матриць, добуток матриць?
4. Чи завжди добуток матриць має властивість комутативності?
5. Що таке граф і як його можна описати матрицею?
6. За якими правилами обчислюють визначники 2, 3 та n!го по!
рядків?
7. Як визначають і знаходять мінор та алгебраїчне доповнення
елемента а
ij
матриці А?
8. Сформулюйте властивості визначника.
9. Дати означення рангу матриці та вказати методи його знаход!
ження.
10. Як визначають та позначають обернену матрицю до матриці А?
11. При яких умовах існує обернена матриця?
12. Які ви знаєте способи знаходження оберненої матриці?
Треба:
a) Визначити матрицю А потреб!пропозицій;
b) Припустимо, що через 5 років потреби інших галузей зростуть
до 24 + N, 33 + N та 75 + N на продукцію галузей 1, 2, З, відповідно.
Скільки продукції повинна виробити кожна галузь, щоб задоволь!
нити нові потреби?
Галузеві
потреби
Галузеві
пропозиції
1 2 3
Потреби
інших
галузей
Кількість
усіх
пропозицій
1 2 40 30 10 100
2 30 20 90 60 200
3 40 100 60 100 300
Витрати праці 10 40 120

106
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Частина 5
СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
У цій частині розглянемо різновиди систем лінійних алгебраїч!
них рівнянь, способи їх дослідження та розв’язування.
5.1. Різновиди систем лінійних алгебраїчних рівнянь
Означення 1. Система алгебраїчних рівнянь називається
лінійною, якщо вона може бути записана у вигляді
11 1 12 2 1 1 1
21 1 22 2 2 2 2
11 2 2
11 2 2
kk nn
kk nn
ii ikk inni
mm mkk mnnm
ax ax ax ax b
ax ax ax ax b
ax ax ax ax b
ax ax ax ax b
, (1)
дe х
1
, х
2
,… x
n
, – невідомі; а
ij
– дійсні числа, які називають коефіцієнтами
системи (індекс
i
вказує рівняння, а індекс
j
невідоме, при якому запи&
сано цей коефіцієнт); b
k
(k = 1, 2,..., m) – вільні (від невідомих) члени або
їх називають правими частинами рівнянь.
Якщо b
k
= 0 для усіх k = 1, 2,..., m, тоді систему називають одно
рідною. Якщо хоча б один вільний член b
k
не дорівнює нулю, тоді си&
стема алгебраїчних рівнянь називається неоднорідною.
Означення 2. Розв’язком системи (1) називається множина
дійсних чисел
12
,,
n
, підстановка яких у систему замість не&
відомих x
1
, х
2
, ..., х
n
, перетворює кожне рівняння системи у тотожність
(іноді кажуть, що ця множина задовольняє систему рівнянь).
Означення 3. Система лінійних алгебраїчних рівнянь, що має
хоча б один розв’язок, називається сумісною, а система, що не має
розв’язку, називається несумісною.

107
Частина 5. Системи лінійних алгебраїчних рівнянь
5.1.1. Теорема Кронекера+Капеллі
Німецький математик Леопольд Кронекер (1823–1891) та італійсь!
кий математик Альфред Капеллі (1855–1910) довели дуже важливу
теорему, яка використовується у багатьох випадках.
Позначимо через А основну матрицю системи (1), яка складена з
коефіцієнтів при невідомих, а через
A
– розширену матрицю цієї
системи, яка одержана шляхом доповнення матриці А стовпцем
вільних членів, тобто
11 12 1
21 22 2
123
;
n
n
mmm mn
aa a
aa a
A
aaaa
11 12 1 1
21 22 2 2
113
n
n
mmm mnm
aa ab
aa ab
A
aaaab
.
Теорема Кронекера+Капеллі. Система лінійних алгебраїч
них рівнянь (1) сумісна тоді і тільки тоді, коли ранг основної
матриці системи дорівнює рангу розширеної матриці
r(А) = r(
A
), (2)
причому, система має єдиний розв’язок тоді і тільки тоді, коли
r(А) = r(
A
) = n. (3)
Приклад 1. Дослідити сумісність системи
1234
1234
12 3 4
1
0
22 0,5
xxxx
xxxx
xx x x
.
Розв’язання. Задана неоднорідна система трьох лінійних ал!
гебраїчних рівнянь з 4 невідомими. Для перевірки умови (2) теоре!
ми КронекераКапеллі знайдемо ранги основної та розширеної
матриць заданої системи, застосовуючи до матриць елементарні пе!
ретворення.
Розширену матрицю одержуємо шляхом дописування до основ!
ної матриці системи стовпця вільних членів.

108
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
1
111 1 1
1111 0
1122 0,5
x
A
111 1 1
00 2 2 1
00 3 3 1,5
.
Еквівалентну матрицю отримали шляхом множення елементів
першого рядка на (–1) та додавання до елементів другого та третьо!
го рядків. Тепер елементи другого рядка помножимо на
3
2
і до!
дамо до елементів третього рядка, а потім поміняємо місцями дру!
гий та третій стовпчики.
11111
00 22 1
00 00 0
A
11 111
0202 1
00 00 0
.
З останнього запису випливає, що
rA
= 2 та r(А) = 2, тобто
r(А) =
rA
, а це означає, що задана система рівнянь є сумісною.
5.1.2. Еквівалентні системи
Означення. 4. Системи лінійних алгебраїчних рівнянь назива&
ють еквівалентними, якщо їх розв’язки співпадають.
Розглянемо довільну систему лінійних алгебраїчних рівнянь виг!
ляду (1). Якщо в цій системі рівняння поміняти місцями, будь!яке
рівняння помножити на дійсне число k
0, тоді розв’язок системи не
зміниться, тобто система матиме інший вигляд, еквівалентний по!
чатковому.
Відомо, що сума скінченного числа доданків не зміниться, якщо
їх поміняти місцями. Тому розв’язок системи не зміниться, якщо ми
в усіх рівняннях доданки з х
k
поміняємо місцями з доданками, які
містять х
і
, але це приведе до перепозначення невідомих. Розв’язок сис!
теми не зміниться, якщо ми будь!яке рівняння системи помножимо

109
Частина 5. Системи лінійних алгебраїчних рівнянь
5.2. Знаходження єдиного розв’язку
Згідно з теоремою Кронекера!Капеллі система лінійних алгебраїч!
них рівнянь має єдиний розв’язок у випадку виконання умов (3),
тобто коли ранг основної матриці системи дорівнює рангу розшире!
ної матриці системи та кількості невідомих.
Розглянемо систему лінійних алгебраїчних рівнянь, яка має од!
накову кількість рівнянь та невідомих, тобто систему вигляду
11 1 12 2 1 1
21 1 22 2 2 2
11 22
nn
nn
nn nnnn
ax ax ax b
ax ax ax b
ax ax ax b
. (4)
Якщо основний визначник
(А) цієї системи (визначник основ!
ної матриці коефіцієнтів цієї системи) не дорівнює нулю, то ранги
основної та розширеної матриць системи будуть рівними і дорівню!
вати кількості невідомих п. Отже, згідно з теоремою Кронекера!Ка!
пеллі така система має єдиний розв’язок.
У випадку b
1
= b
2
= ... = b
n
= 0 система (4) однорідна, її єдиний
розв’язок тривіальний, тобто
12
0
n
xx x
.
Якщо система (4) неоднорідна, її єдиний розв’язок можна знахо!
дити різними способами.
У випадку, коли кількість рівнянь та невідомих
3
n
, часто ви!
користовують правило Крамера або матричний метод розв’язування.
У випадку, коли
3
n
доцільно використовувати метод Гаусса (при!
ведення системи до трикутного вигляду) або більш ефективний ме!
тод – метод Гаусса!Жордана.
на дійсне число k
0 і додамо почленно до іншого рівняння системи.
Вказані перетворення системи називають елементарними перетворен!
нями системи. Доцільно замість системи рівнянь розглядати її роз!
ширену матрицю та робити перетворення з цією матрицею. Саме такі
елементарні перетворення були проведені при розв’язуванні прикла!
ду 1.

110
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Слід зауважити, що правило Крамера та матричний метод можна
застосовувати і для великих значень n, але вони потребують більше
часу і багато розрахунків.
Ознайомимось з матричним методом та правилом Крамера у цьо!
му розділі. Найбільш досконалий метод Гаусса!Жордана розглянемо
у розділі 5.3.
Правило Крамера (швейцарський математик, 31.07.1704–
04.01.1752). Якщо основний визначник
(А) неоднорідної системи n в
лінійних алгебраїчних рівнянь з n невідомими не дорівнює нулю, то ця
система має єдиний poзв’язок, який знаходять за формулами
,
k
k
x
A
1, 2, ,kn
, (5)
де
k
– допоміжний визначник, який одержують з основного визначника
(А) шляхом – заміни його k&го стовпця стовпцем вільних членів сис&
теми.
Приклад 2. Розв’язати за правилом Крамера систему рівнянь
123
123
12 3
25 2
234 8
4313
xxx
xxx
xx x
.
Розв’язання. Задана неоднорідна система 3 лінійних алгебраїч!
них рівнянь з трьома невідомими. Основний визначник цієї системи
125
2 3 4 9 32 10 60 12 4 31 0
41 3
A
.
Тому, згідно з правилом Крамера, задана система має єдиний роз!
в’язок, який знайдемо за формулами (5).
Спочатку знайдемо допоміжні визначники:
