Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.

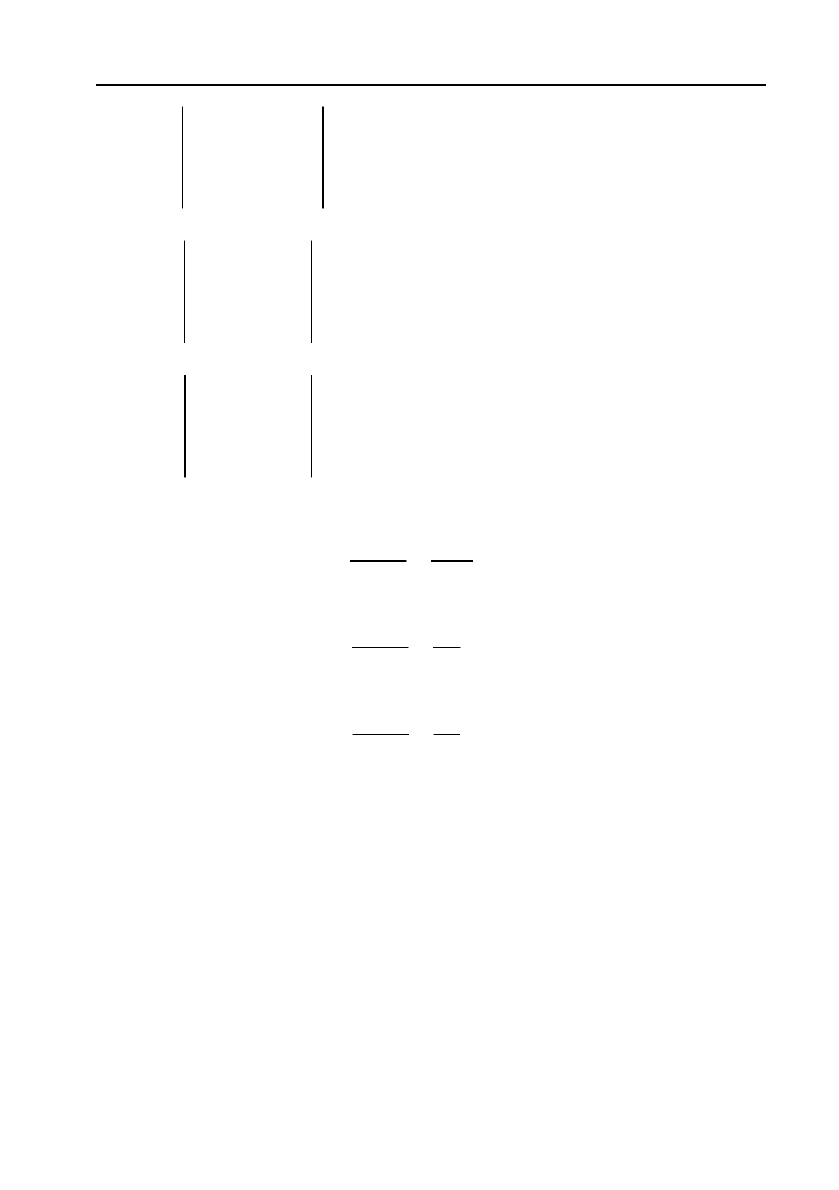
111
Частина 5. Системи лінійних алгебраїчних рівнянь
1
225
8 3 4 18 104 40 195 48 8 93
13 1 3
,
2
125
2 8 4 24 32 130 160 12 52 62
4133
,
3
12 2
23 8396442452831
41 13
.
Тепер за формулами (5) знаходимо:
1
1
93
3
31
x
A
,
2
2
62
2
31
x
A
,
3
3
31
1
31
x
A
.
Отже, розв’язком цієї системи буде (–3; 2; 1).
5.2.1. Матричний метод
Якщо позначити
11 12 1
21 22 2
12
,
n
n
nn nn
aa a
aa a
A
aa a
1
2
,
n
x
x
X
x
1
2
.
n
b
b
B
b

112
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
то згідно з правилом множення матриць та умовою рівності матриць
одержимо запис системи лінійних алгебраїчних рівнянь
11 1 12 2 1 1
21 1 22 2 2 2
11 22
nn
nn
nn nnnn
ax ax ax b
ax ax ax b
ax ax ax b
(4)
у матричній формі:
AX B
. (6)
Якщо матриця А квадратна порядку п і її визначник
(А) не
дорівнює нулю, тоді існує обернена до А матриця А
–1
, тому можна
рівність (6) помножити на А
–1
зліва. Одержимо
А
–1
АX = А
–1
В. (7)
За означенням оберненої матриці маємо:
А
–1
А = Е,
тому (7) прийме вигляд:
ЕХ = А
–1
В.
Але множення матриці!стовпця X на матрицю Е не змінює X,
тобто ЕХ = X. Таким чином, одержуємо формулу:
Х = А
–
1
В. (8)
за якою і знаходять розв’язок системи (4) матричним методом.
Отже, матричний метод можна застосовувати у випадку, коли
квадратна матриця А має не рівний нулю визначник.
Для розв’язування неоднорідної системи n лінійних алгебраїчних
рівнянь з n невідомими матричним методом доцільно здійснювати
такий порядок дій:
1. Записати основну матрицю системи А і знайти її визначник
(А). Якщо
(А) = 0, то система розв’язку не має.
2. Якщо
(А)
0, тоді знайти обернену матрицю А
–
1
до матриці А.
3. Помножити обернену матрицю А
–
1
на матрицю!стовпець
вільних членів системи. Одержаний при цьому стовпець згідно з
формулою (8) і буде розв’язком системи.

113
Частина 5. Системи лінійних алгебраїчних рівнянь
Приклад 3. Знайти розв’язок заданої системи матричним ме!
тодом
123
13
12 3
1
21
22
xxx
xx
xx x
.
Розв’язання. Основною матрицею заданої системи буде матриця
111
10 2
21 1
A
.
Визначник цієї матриці
111
10 241126
21 1
A
.
Для запису оберненої матриці А
–
1
знайдемо алгебраїчні доповнен!
ня елементів матриці А:
11
02
2;
11
A
21
11
0;
11
A
31
11
2;
02
A
12
3;A
22
3;A
32
3;A
13
1;A
23
3;A
33
1.A
Отже,
1
202
1
333.
6
131
A
Тепер за формулою (8) знаходимо розв’язок заданої системи:
1
2021 21 01 22 6 1
11 1
333 1 31 3 1 32 6 1.
66 6
1312 11 3112 6 1
XAB

114
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Вправи до розділу 5.2
N – номер варіанта.
1. За правилом Крамера розв’язати системи рівнянь:
a)
2
11
22
xy z N
xN y z
xy z N
; b)
23 22
0
26
NxyzN
xyz
xyz
;
c)
23
0
221
xy z
xy z
xy N z N
; d)
32
23 4
0
x
N
y
zN
xyz
xyz
.
2. Розв’язати системи матричним методом
a)
3
20
13 0
xy
zN
xNyz
Nx yz
; b)
2
0
10
xy z N
xNy z
xy N z
;
c)
2
0
32 1 1
xy
zN
Nx y
xyNz
; d)
2
1
21 220
xy
zN
Nx y z
Nx yz
;
e)
0
2
11
Nx y z
xy
zN
xyNz
.

115
Частина 5. Системи лінійних алгебраїчних рівнянь
5.3. Методи Гаусса та Гаусса+Жордана
Система лінійних алгебраїчних рівнянь має нескінченну кількість
розв’язків у таких випадках:
1. Коли однорідна система має п рівнянь з п невідомими і її ос!
новний визначник
(А) дорівнює нулю.
2. Коли кількість рівнянь неоднорідної системи не дорівнює
кількості невідомих, а система рівнянь є сумісною.
3. Коли кількість рівнянь дорівнює кількості невідомих та дорів!
нює n, система рівнянь сумісна r(А) = r(
A
) = r але r < n.
Видатний німецький математик, астроном, фізик і геодезист Карл
Фрідріх Гаусс (30.04.1777–23.02.1855) розробив метод розв’язування
таких систем лінійних алгебраїчних рівнянь. Суть метода Гаусса
полягає в тому, що шляхом елементарних перетворень систему тре!
ба привести до трикутного вигляду, коли усі елементи головної діа!
гоналі основної матриці системи дорівнюють 1, а елементи основної
матриці, що знаходяться нижче її головної діагоналі, дорівнюють
нулю. Такий вигляд системи дозволяє знайти усі невідомі. Метод
Гаусса можна застосовувати і до систем лінійних алгебраїчних
рівнянь, що мають єдиний розв’язок.
Щоб краще зрозуміти суть метода Гаусса, розглянемо декілька
прикладів.
Приклад 1. Розв’язати систему рівнянь
2431
243
352
xyz
xyz
xy z
.
Розв’язання. Спочатку поміняємо місцями перше та друге
рівняння, щоб елемент а
11
основної матриці дорівнював 1. Одержимо:
243
2431
352
xyz
xyz
xy z
.
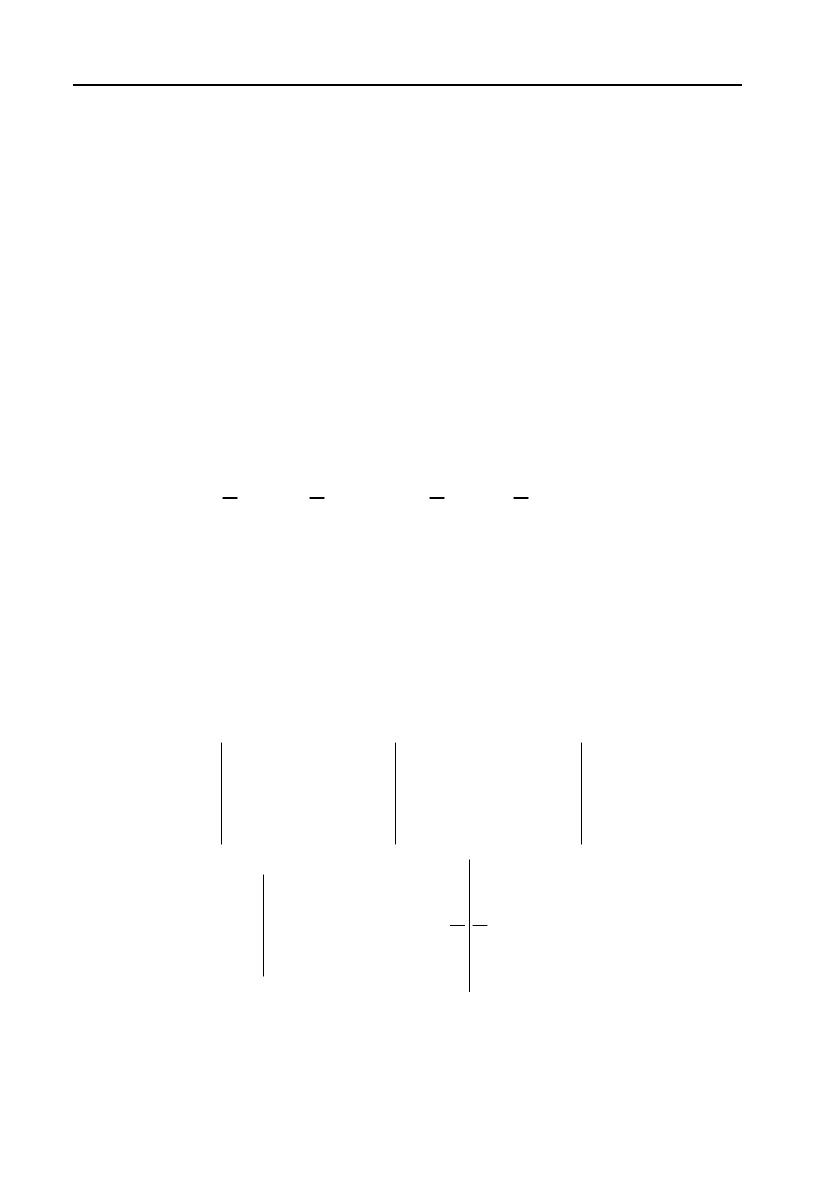
116
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Тепер перше рівняння помножимо на (–2) і додамо до другого
(щоб одержати а
21
= 0), а потім помножимо перше рівняння на (–3)
і додамо до третього рівняння (щоб одержати а
31
= 0). Тоді будемо
мати систему
24 3
55
57 7
xyz
z
yz
.
Тепер друге рівняння поділимо на (–5), третє рівняння поділимо
на 5 і поміняємо їх місцями. Одержимо систему трикутного вигляду:
20
24 3 341
1
77 77
10
55 55
1
11
xy z x
x
yz y y
z
zz
.
Отже, система має єдиний розв’язок (–1, 0, 1).
Зауваження. Елементарні перетворення доцільно виконувати
не з усією системою, а з її розширеною матрицею. Розв’язання при&
кладу 1 у такий спосіб виглядає так:
2 4 31 1 2 43 1 2 4 3
1 2 43 2 4 31 0 0 5 5
3152 3152 05 77
1243
1243
77
05 77 01 .
55
00 55
00 11

117
Частина 5. Системи лінійних алгебраїчних рівнянь
Приклад 2. Розв’язати систему рівнянь
12 3 4
134
234
22
433
23 1
xx x x
xxx
xxx
.
Розв’язання. Задана система 3!х рівнянь з 4!ма невідомими. Ви!
конаємо елементарні перетворення з розширеною матрицею.
21 1 12 2 1 1 12 2 1 1 12
40 1 33 0 2 3 11 0 2 3 11
02 3 11 0 2 311 0 0 0 00
.
Звідси випливає, що основна та розширена матриці мають рівні
ранги: r(А) =
2.rA
Знайдемо мінор другого порядку, який не
дорівнює нулю. Наприклад:
21
0
02
.
Мінор, який не дорівнює нулю, та має порядок, рівний рангу
r = r(А) = r(
A
), називають базисним мінором, тому обраний нами
мінор – базисний.
Невідомі х
1
та х
2
, для яких елементи базисного мінора є кое!
фіцієнтами, називають базисними невідомими. Інші невідомі систе!
ми х
3
та х
4
– вільні. Останній вигляд розширеної матриці відповідає
такій системі
12 34 1234
234 2 34
22
22
23 2 3
11
xx xx xxxx
xxx x xx
.
Вільні невідомі перенесли у праву частину системи. Ми одержа!
ли базисні змінні х
1
та х
2
як функції х
3
та х
4
:

118
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
2
13 4
134
234
234
133
22
444
31 1
311
22 2
222
x
xx x
xxx
xxx
xxx
.
Вільним невідомим х
3
та х
4
можна надавати будь!які значення:
х
3
= С
1
, х
4
= С
2
, де С
1
та С
2
– довільні сталі. Отже, одержуємо нескінчен!
ну кількість розв’язків системи вигляду:
12
1
2
12
3
1
4
2
3
3
444
3
1
222
CC
x
x
CC
X
x
C
x
C
.
5.3.1. Поняття різновидів розв’язків
Розв’язки прикладу 2 приймають різні значення, якщо сталим С
1
та С
2
надавати конкретні значення.
Коли розв’язок розглядають залежним від будь!яких значень С
1
та С
2
, тоді його називають загальним розв’язком відповідної сис
теми лінійних алгебраїчних рівнянь.
Якщо взяти С
1
= С
2
= 0, то одержаний розв’язок називають ба
зисним. У випадку прикладу 2 базисним розв’язком буде:
3
4
1
2
0
0
b
X
.

119
Частина 5. Системи лінійних алгебраїчних рівнянь
Якщо одній сталій надати значення 0, а іншій 1, тоді одержані
розв’язки називають фундаментальними.
У системі прикладу 2 є два фундаментальних розв’язки:
,1
3
2
0;
0
1
ф
X
,2
1
2
2
1
0
ф
X
.
Невід’ємний базисний розв’язок називають опорним розв’язком
системи лінійних алгебраїчних рівнянь.
Саме базисні, фундаментальні та опорні розв’язки систем найча!
стіше використовують економісти.
Головною метою дисципліни «Математичне програмування» є
розробка методів знаходження опорних розв’язків та вибору опти!
мального розв’язку серед них.
5.3.2. Метод Гаусса+Жордана з використанням розрахункових
таблиць
В економічних дослідженнях дуже часто необхідно розв’язувати
системи лінійних алгебраїчних рівнянь з багатьма невідомими і ме!
тод Гаусса для них не дуже зручний тому, що після приведення мат!
риці системи до трикутного вигляду треба ще провести певну
кількість розрахунків, щоб одержати усі невідомі.
Метод Гаусса буде досконалішим, якщо при елементарних пере!
твореннях можна одержати рівними нулю не тільки елементи, що
лежать нижче головної діагоналі, а й ті елементи, що лежать вище
головної діагоналі. Саме цього вдається добитися методом Гаусса!
Жордана, який треба обов’язково зрозуміти і оволодіти розробленою
економістами технікою його застосування з використанням розрахун!
кових таблиць.
Перетворення Гаусса!Жордана дозволяють розв’язувати довільні
системи лінійних алгебраїчних рівнянь, знаходити ранг матриці, обер!
нену матрицю.
120
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
При розв’язуванні довільних систем лінійних алгебраїчних
рівнянь методом Гаусса!Жордана треба послідовно зробити декілька
кроків перетворення Гаусса!Жордана з певним правилом переходу
від однієї таблиці до іншої.
Кроком перетворення ГауссаЖордана називають елементарні
перетворення (множення рівнянь на число, алгебраїчна сума різних
рівнянь), за допомогою яких задана система зводиться до еквівалент!
ної системи.
Алгоритм кроку перетворення Гаусса+Жордана
1. Обираємо розв’язувальний елемент
0
ij
a
.
2. Елементи
i
&го рядка (його називають розв’язувальним) ділимо
на
ij
a
і запишемо в
i
рядок розрахункової таблиці.
3. В розв’язувальному
j
стовпці замість
ij
a
пишуть одиницю, а
замість інших елементів цього стовпця пишуть нулі.
4. Усі інші елементи розрахункової таблиці, в тому числі і конт&
рольного стовпця, знаходять за формулою
1, 2, , ; 1, 2, , ; , .
ij kl kj il
kl
ij
aa aa
a
a
kmlnkijl
(1)
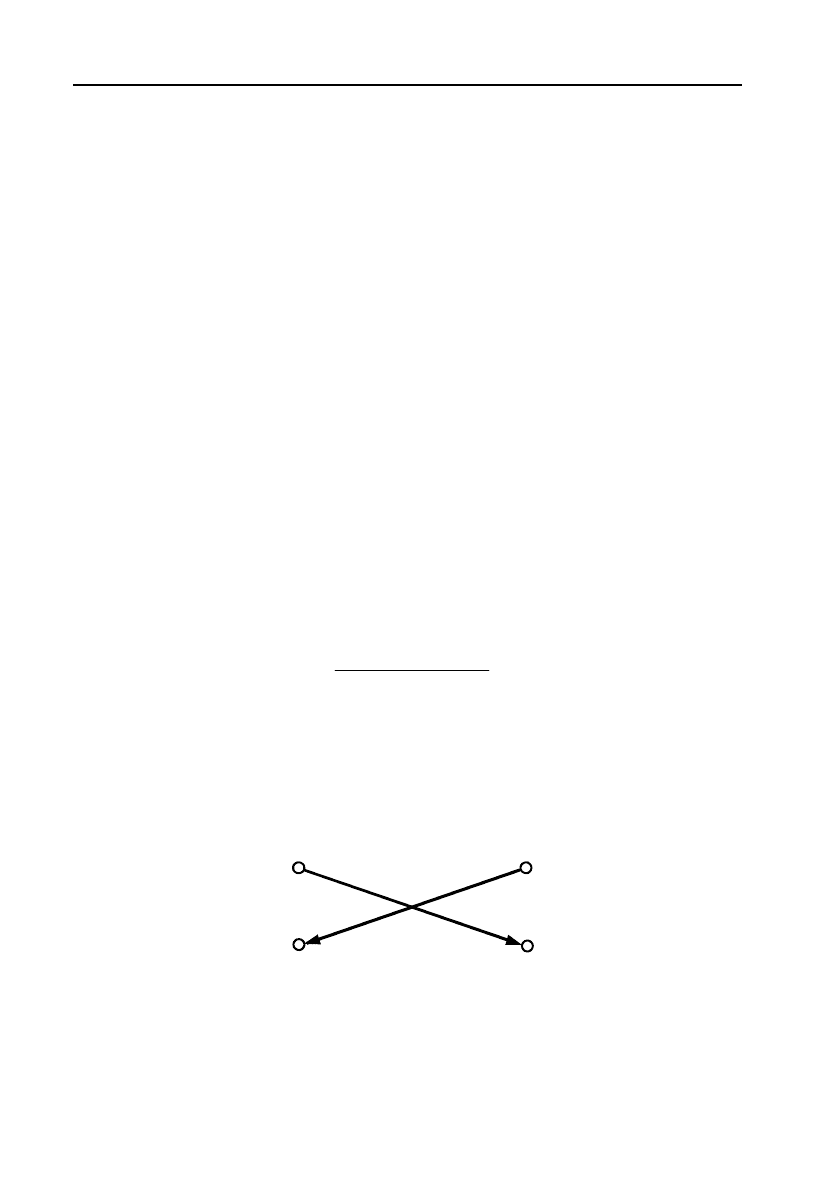
Обчислення елементів
kl
a
за формулою (1) доцільно виконувати з
використанням схеми прямокутника
5. Роблять перевірку правильності розрахунків шляхом порівнян&
ня суми елементів рядка з відповідним елементом контрольного
стовпця.
il
a
kl
a
ij
a
kj
a
