Барковський В.В., Барковська Н.В. Вища математика для економістів
Подождите немного. Документ загружается.


81
Частина 4. Матриці та визначники
4.2. Найпростіші дії з матрицями
Найпростішими діями з матрицями називають множення мат&
риці на число, їх додавання та віднімання, множення матриць.
Добутком матриці А на число k називається матриця, елемен!
ти якої дорівнюють добуткам елементів матриці А та числа k:
11 12 13 1
21 22 23 2
123
...
...
... ... ... ... ...
...
n
n
mm m mn
ka ka ka ka
ka ka ka ka
kA
ka ka ka ka
. (1)
Додавати та віднімати можна лише матриці однакового розміру.
Алгебраїчною сумою матриць А та В однакового розміру
mn
називається матриця С розміру
mn
, елементи якої
ij
c
дорів!
нюють відповідній алгебраїчній сумі елементів
ij
a
та
ij
b
матриць А
та В, тобто
11 11 12 12 1 1
21 21 22 22 2 2
11 22
nn
nn
mm m m mnmn
ab ab ab
ab ab ab
ABC
abab ab
. (2)
Наприклад, якщо
50 30 40
18 16 12
A
,
20 18 20
14 15 10
B
,
тоді
розміру
34
. Кожен рядок та кожен стовпець цієї матриці має певний
зміст. Наприклад, елементи другого рядка вказують кількість витраче!
ного матеріалу Y на виробництво продукції А, В, С та D; елементи дру!
гого стовпця матриці вказують кількість витрачених матеріалів X, Y та
робочих годин на виробництво продукції В.

82
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
50 20 30 18 40 20 70 48 60
18 14 16 15 12 10 32 31 22
AB
.
Розглянемо ще один приклад. Якщо матриця F відповідає вироб!
ничим параметрам за перший квартал року, а матриця Q, побудова!
на по даним тих же параметрів за другий квартал року, тоді F + Q
буде характеризувати ці параметри за перший та другий квартали,
тобто за півроку.
Для знаходження добутку АВ матриць А та В необхідно, щоб
кількість стовпців матриці А (першого множника) дорівнювала
кількості рядків матриці В (другого множника). Добутком АВ мат!
риці А розміру
mn
і матриці В розміром
np
називається матри!
ця С розміром
mp
, елементи якої с
ij
дорівнюють сумі добутків
елементів і&го рядка матриці А на відповідні елементи j!гo стовпця
матриці В, тобто кожен елемент матриці С знаходять за формулою
11 22 3 3ij i j i j i j in nj
cababab ab
. (3)
Зауваження. Добуток матриць взагалі не має властивості ко&
мутативності, тобто АВ
ВА. Якщо добуток двох матриць має вла&
стивість АВ = ВА, тоді кажуть, що матриці комутують.
Приклад 2. Знайти добуток матриць
11 12 13
21 22 23
31 32 33
aaa
A
aaa
aaa
та
1
2
3
x
Xx
x
.
Розв’язання. У матриці А три стовпця, у матриці X три рядки,
тому ці матриці можна множити. Добутком цих матриць буде мат!
риця!стовпець
11 12 13 1 11 1 12 2 13 3
21 22 23 2 21 1 22 2 23 3
31 32 33 3 31 1 32 2 33 3
a a a x ax ax ax
AX a a a x a x a x a x
aaa x ax ax ax
. (4)

83
Частина 4. Матриці та визначники
Приклад 3. Нехай
123
456,
214
A
212
321
132
B
,
знайти АВ та ВА.
Розв’язання.
123 212 12 2331 149 226
456 3 21 42 5361410188512
214 1 32 2 2 1341 2212 418
71410
13 32 25 ,
31613
AB
212 123 244 452 668
321456 38261019124
1 32 214 1124 21523188
638
13 17 25 .
17 19 29
BA
Отже,
.
AB BA
Зауваження. Ділення матриць
A
B
poзглядають як добуток АВ
–1
,
де В
–1
– матриця, обернена до матриці В, визначення та знаходжен&
ня якої розглянемо пізніше, після введення нових понять.
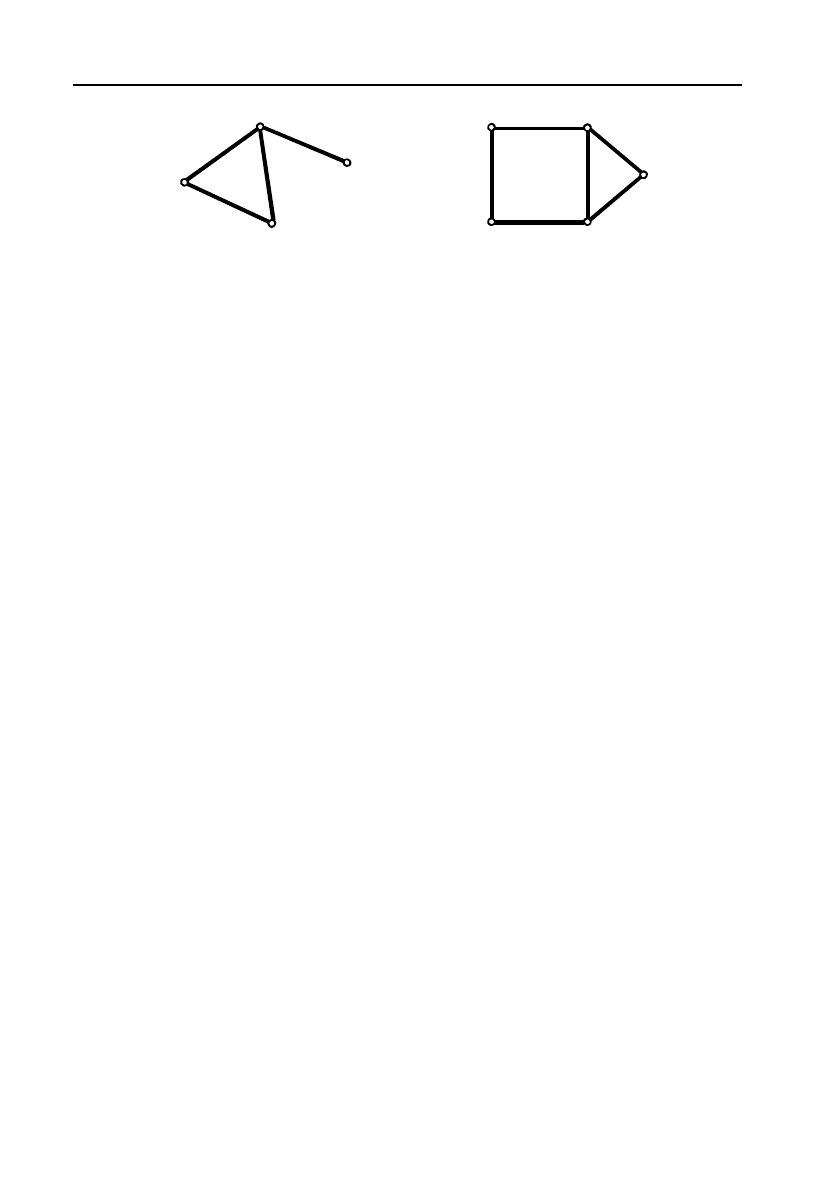
Приклад 4. (З теорії графів). Графом називають певну
кількість точок (його вершин), деякі з них з’єднані лініями (ребра!
ми). На малюнку 1 задані два графи з 4 та 5 вершинами.
84
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Мал. 1.
Занумеруємо вершини цифрами 1, 2, 3, ... та визначимо матрицю
А з елементами
ij
a
таким чином:
1, ' ;
0, ' .
ij
якщо вершини i та j зєднаніребром
a
я
кщо вершини i та j не з єднані ребром
Треба побудувати матриці А та А
2
для випадків a) та b), зображе!
них на малюнку 1. Показати, що елемент з індексами ij матриці А
2
визначає кількість шляхів довжини 2 (двох послідовно пройдених
ребер) з вершини і у вершину j графа.
Розв’язання.
У випадку а) згідно з визначенням елементів
ij
a
одержуємо мат!
рицю
0100
1011
.
0101
0110
A
Матриця А
2
буде мати вигляд
2
01000100 1011
10111011 0311
.
01010101 1121
01100110 1112
A
1
2
3
4
а)
12
3
45
b)

85
Частина 4. Матриці та визначники
Розглянемо зміст елементів А
2
. Елементи і!го рядка цієї матриці
рівні кількості вказаних в умові напрямків з точки і. Так, точка і = 1
має лише один напрямок, що пов’язує її з вершиною 2, що не дорів!
нює j = 1, тобто а
11
= 1; а
12
= 0 тому, що не має інших ребер між
точкою 1 та 2; а
13
= 1 та а
14
= 1 тому, що точка 1 має лише одне ребро,
що зв’язує її з точкою 2, 2
3, 2
4.
У випадку b) згідно з визначенням елементів а
ij
та вигляду по!
єднань вершин, зображених на малюнку 1, b) маємо:
01001
10110
.
01010
01101
10010
A
Ця матриця квадратна п’ятого порядку, тому А
2
також буде квад!
ратною матрицею п’ятого порядку, а саме
2
01001 01001 20110
10110 10110 03112
.
01010 01010 11211
01101 01101 21 130
10010 10010 02102
A
Вправи до розділів 4.1 та 4.2
1. Задані матриці:
234
04 5;
20 3
A
31 2
04 1;
103
B
1
2
3
;
x
X
x
x
1
2
3
;
y
Yy
y

86
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
7
2;
6
C
23
;
12
D
10
;
21
H
1
2
3
.
z
Z
z
z
Знайти:
1. Розмір кожної з цих матриць.
2. Матрицю F = (N + 1)А – (N + 2)В.
3. Коли виконуються рівності: а) АХ = С; b) АХ = Y; c) BY = Z?
4. За допомогою якої матриці можна представити матрицю Z че!
рез матрицю X, якщо Z = BY, Y = АХ?
5. Обчислити D
2
– Н
2
та (D – H)(D + Н) і показати, що
D
2
– H
2
(D – H)(D + H).
6. Записати наступні системи лінійних алгебраїчних рівнянь у
матричній формі
a)
237
48
xy
xy
; b)
324
457
xy
xy
; c)
238
2413
325
xyz
xy z
yz
;
d)
123
341
12 3 4
234 5
35 7
2
xxx
xxx
xx x x
; e)
23
347
59
xy
yz
zx
.
7. При виробництві своєї продукції фірма використовує 4 різних
види сировини М
1
,
М
2
,
М
3
, та М
4
вартістю 5, 7, 6 та 3 гривні за одини!
цю виміру. На виготовлення одиниці продукції потрібно 4(N + 1),
3(N – 1), 2(N + 1) та 5(N + 1) одиниць відповідного виду сировини.
Виразити загальну вартість сировини потрібної для виготовлення
одиниці виробу, як добуток двох матриць.
8. Фірма використовує три різних види сировини М
1
, М
2
та М
3
,
для виробництва двох видів продукції Р
1
та Р
2
. Для виготовлення кож!
ної одиниці Р
1
потрібно 3, 2 та 4 одиниці сировини М
1
, М
2
та М
3
, а для
виготовлення кожної одиниці Р
2
потрібно 4, 1, 3 одиниць сировини,

87
Частина 4. Матриці та визначники
відповідно. Припустимо, що фірма виготовляє (N + 2)
20 одиниць
виробів Р
1
та 30(N + 2) одиниць виробів Р
2
кожного тижня. Знайти:
a) необхідну щотижневу кількість сировини;
b) вартість сировини для виготовлення одиниць виробів Р
1
та Р
2
,
якщо вартість одиниці сировини М
1
, М
2
та М
3
, буде 6, 10 та 12 гри!
вень;
c) чому дорівнюють загальні щотижневі витрати виробництва
продукції Р
1
та Р
2
?
9. Знайти добуток матриць АВ або ВА.
а)
43 2A
,
1
3;
5
B
b)
3
2
5
A
,
441B
;
c)
11 2
312
A
,
2
2;
5
B
d)
34 1
452
A
,
21
;
31
01
B
e)
3141
203 1
1342
A
,
12
31
;
42
25
B
f)
58 4
69 5
47 3
A
,
325
413.
965
B
88
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
4.3. Визначники
Визначником nго порядку квадратної числової матриці А по
рядку п називають число, яке знаходять з елементів матриці А за
певним правилом і позначають |А| або
(А).
Правило знаходження визначника 2 порядку. Визначник дру!
гого порядку дорівнює різниці добутків елементів головної та допо!
міжної діагоналей, тобто
11 12
11 22 21 12
21 22
aa
aa aa
aa
. (1)
Схему цієї формули можна зобразити таким чином
Знак (+) вказує, що добуток елементів головної діагоналі треба
брати зі своїм знаком, знак (–) означає, що добуток елементів него!
ловної діагоналі треба брати з протилежним знаком.
Приклад 1. Обчислити визначники:
a)
23
45
; b)
32
04
; c)
25
68
.
Розв’язання. Будемо обчислювати задані визначники за фор!
мулою (1):
a)
23
2 5 3 4 10 12 22
45
;
b)
32
34 02 12
04
;
11
a
22
a
12
a
21
a
«–»
«+»
11 22 21 12
aa aa
89
Частина 4. Матриці та визначники
c)
25
2 8 5 6 16 30 14
68
.
Правило знаходження визначника 3го порядку. Визначник
третього порядку знаходять за формулою
11 12 13
21 22 23 11 22 33 12 23 31 21 32 13
31 32 33
aaa
a a a aaa aaa aaa
aaa
(2)
13 22 31 12 21 33 32 23 11
aaa aaa aaa
.
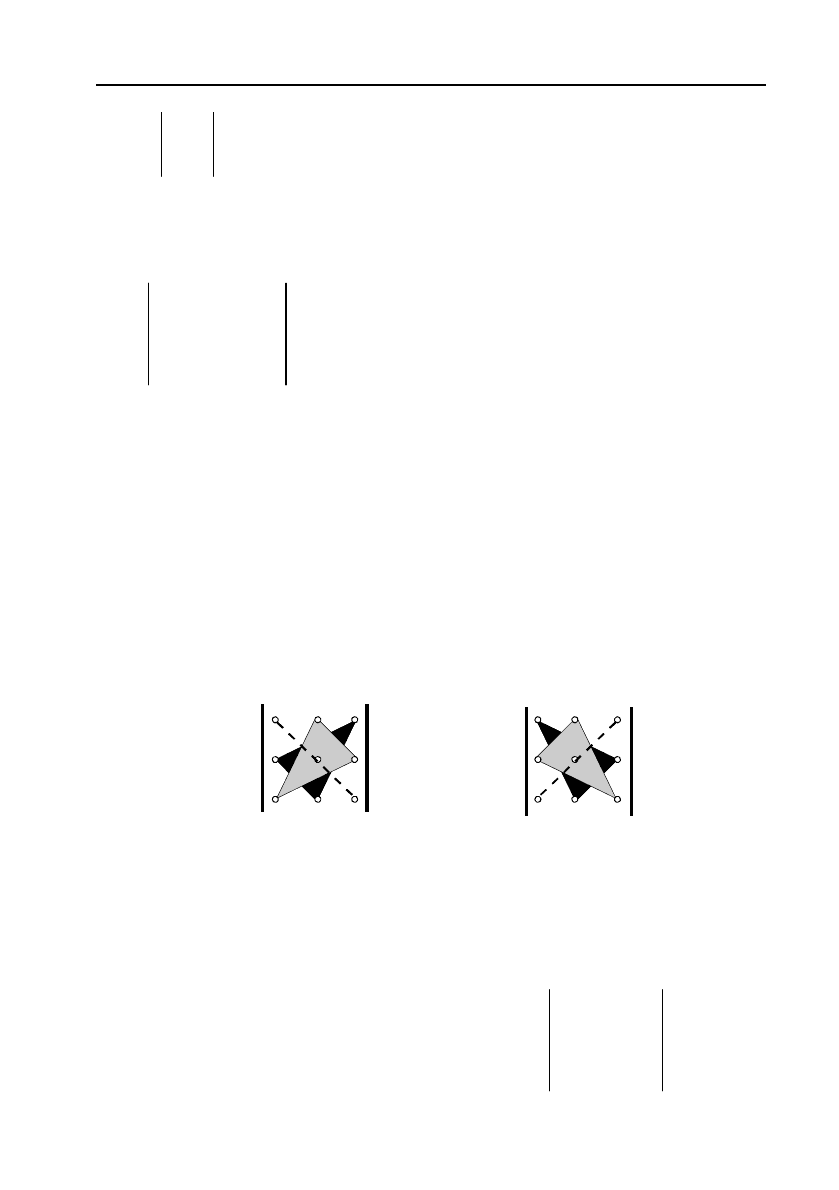
Кожен доданок у правій частині (2) має 3 множники з різних
рядків та стовпців. Три перших доданка із знаком (+) є добутками
елементів головної діагоналі і елементів вершин трикутників з осно!
вами паралельними головній діагоналі (дивись схему а) малюнка 1).
Три останні доданки у правій частині (2) мають від’ємний знак. Вони
є добутками елементів неголовної діагоналі та елементів вершин три!
кутників із основами паралельними неголовній діагоналі (мал. 1, b).
Мал. 1.
Ця схема обчислення визначника третього порядку називається
правилом Саріуса. Існують також інші схеми обчислення визнач!
ника 3!го порядку.
Приклад 2. Обчислити визначник
230
143
560
.
а)
b)
(+)
(–)

90
Барковський В.В., Барковська Н.В. «Вища математика для економістів»
Розв’язання. Згідно з формулою (2) одержимо
230
1 4 3 240 3 3 5 160 5 40 1 3 0
560
362045000369
.
Для обчислення визначників порядку n > 3 використовують ал!
гебраїчні доповнення та вказане нижче правило.
Означення 1. Мінором М
ij
елемента а
ij
визначника nго по
рядку називається визначник (n – 1) порядку, який одержуємо з виз&
начника |А| шляхом викреслювання і&го рядка та j&го стовпця, на пе&
ретині яких знаходиться елемент а
ij
.
Означення 2. Алгебраїчним доповненням А
ij
елемента а
ij
визначника називають мінор цього елемента, взятий зі знаком (–1)
i+j
,
тобто
1
ij
ij ij
AM
. (3)
Приклад 3. Знайти алгебраїчні доповнення до елементів а
21
,
та а
33
визначника
23 1
142
31 4
.
Розв’язання. Алгебраїчні доповнення до елементів а
21
та а
33
по!
значимо А
21
та А
33
, відповідно. Згідно з означенням 2
А
21
= (–1)
2+1
М
21
= –М
21
; А
33
= (–1)
3+3
М
33
= М
33
.
(4)
Мінори М
21
та М
33
знайдемо згідно з означенням 1:
21
23 1
31
142 34 1112113
14
31 4
M
