Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 165

≡

< 1 ,

an acceptable approximation can be obtained for the displacement by treating the

beam as a rigid body (i.e. by including only the strain energy in the springs). What

would be the equivalent simplifying approximation for the case

≫1 and how large

would

need to be for this approximation to be within 5% of the exact answer?

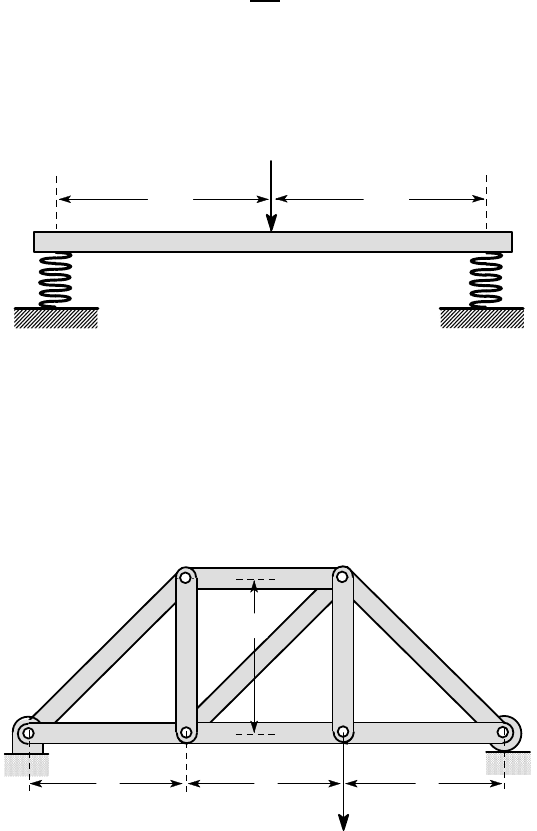
3.12. The determinate truss of Figure P3.12 is simply-supported at its ends A,D and

loaded by a vertical force F at C. All the members have cross-sectional area A and

are of a material with Young’s modulus E. Find the vertical displacement u under the

load at C.

3.13. The cranked bar of Figure P3.13 is built in at A and loaded by an out-of-plane

force F at C, so that the segment BC is loaded in bending and the segment AB in

both bending and torsion. If the bar has a solid circular cross section with diameter

d and the elastic properties are E,

, ﬁnd the vertical displacement u at C. Note that

G= E/2(1 +

L /

Figure P3.11

Figure P3.12

166 3 Energy Methods

Figure P3.13

Sections 3.4, 3.5

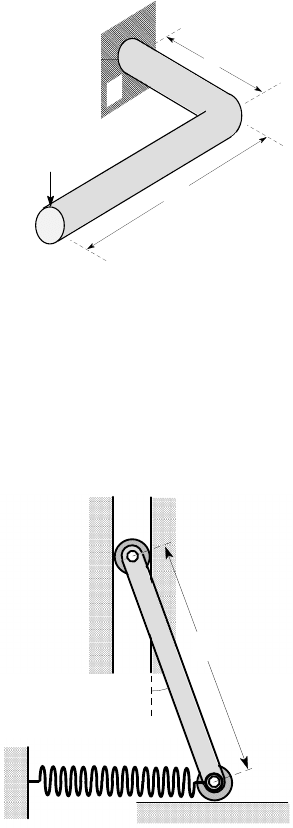
3.14. The uniform rigid bar in Figure P 3.14 is of weight W and slides without fric-

tion. The linear spring is unstretched when the bar is vertical. Use the principle of

stationary potential energy to ﬁnd equilibrium values of

in terms of W, k and L.

What condition must be satisﬁed in order that the position

= 0 should be one

of stable equilibrium.

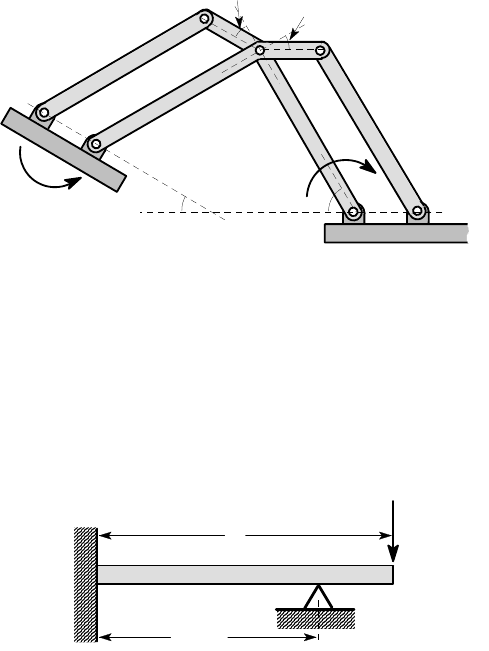
3.15. Figure P3.15 shows a mechanism consisting of a set of pin-jointed rigid bars,

constrained by a spring of stiffness k connecting the points BC. A force F is applied

at E. Find a kinematic relation between the vertical displacement of the force u

and

the extension of the spring. This relation should not be restricted to the case of small

Figure P3.14

Problems 167

displacements — i.e. it must also describe the case where the angle of rotation of CE

is not small. Use the result and the principle of stationary potential energy to deduce

the (non-linear) relationship between u

and F.

L /

Figure P3.15

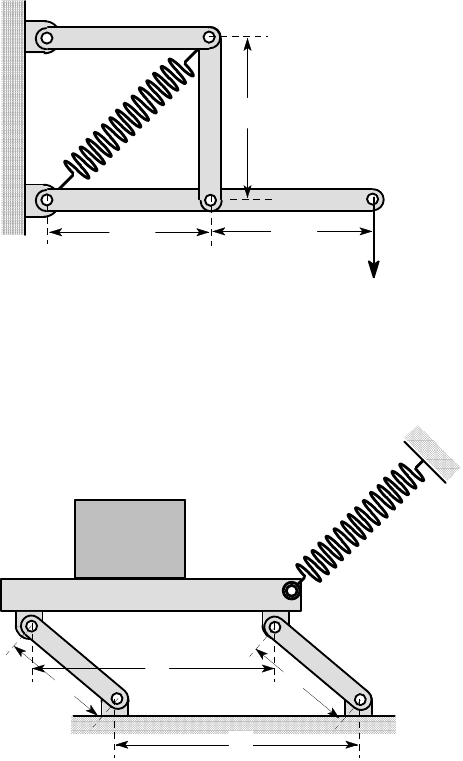
3.16. Use an energy argument to prove that the extension of the spring in Figure

P3.16 is independent of the position of the mass M on the platform AB.

Figure P3.16

This type of mechanism is used in the design of weighing machines, in order that

the measured weight be not dependent on the location of the mass.

3.17. The pin-jointed structure of Figure P3.17 consists of three rigid links each of

length L constrained by two springs on the diagonals, whose stiffnesses and original

lengths are k

and k

respectively.

168 3 Energy Methods

Figure P3.17

If no external forces are applied, the structure is found to adopt an equilibrium

conﬁguration in which

=60

. Show that the ratio of spring stiffnesses must satisfy

the relation

√

3 −L)

−L)

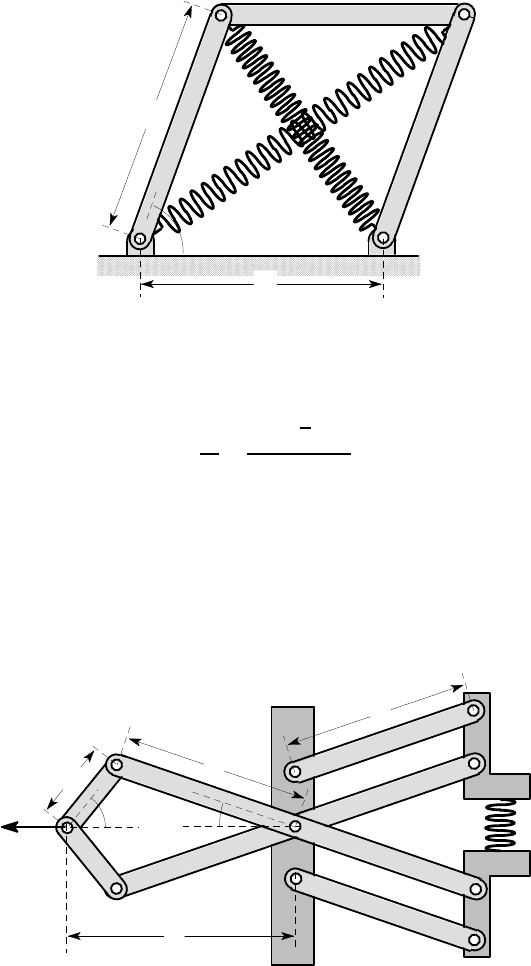
3.18. Figure P3.18 shows a mechanism of rigid pin-jointed links such that a horizon-

tal force F applied at A causes the spring BC to be compressed. Use the principle of

stationary potential energy to ﬁnd the relationship between the force F and the angle

, if the spring has stiffness k and is relaxed when

=30

. You may restrict attention

to solutions in the range 0<

<90

Figure P3.18

Problems 169

3.19. Figure P3 .19 shows an aircraft door-closing mechanism. The door DE and the

links ABC,EBF,CD,FG can be treated as rigid and all the connections are friction-

less pin joints. The quadrilaterals ABFG and BCDE are parallelog rams. Motio n at

A is resisted by a torsion spring that exerts a moment M in the direction shown of

magnitude

M = K(

) ,

where K,

are constants. A moment T is applied to the door DE as shown. Find the

relationship between T and

Figure P3.19

Section 3.6

3.20. Figure P3.20 shows a beam of length L an d ﬂexural rigidity EI, which is built-in

at z = 0 and simply supp orted at the in te rmediate point z = 3L/4. Use the Rayleigh-

Ritz method with one degree of freedom to estimate the deﬂection at the free end.

3L /4

Figure P3.20

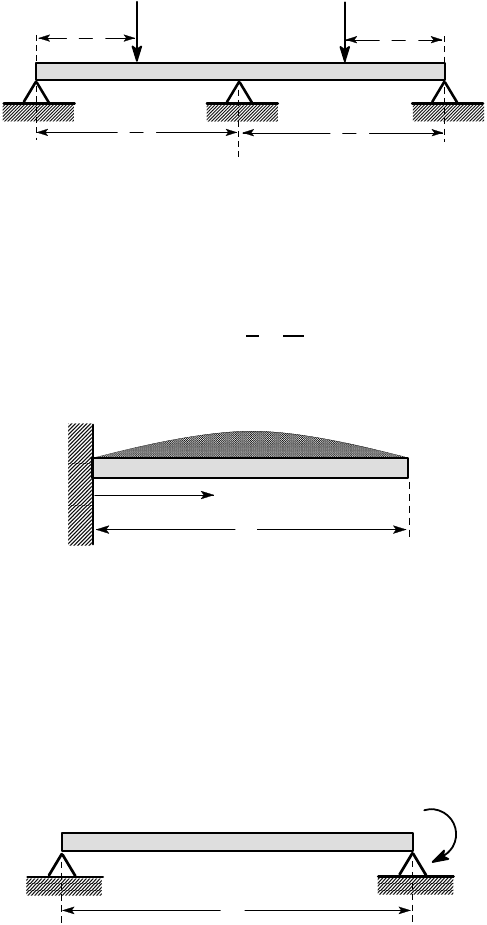
3.21. Figure P3.21 shows a beam of len gth L and ﬂexural rigidity EI, which is built-

in at z = 0, simply su pported at z = L, and subjected to a uniformly distributed load

per unit length. Use the Rayleigh-Ritz method with one degree of freedom to

estimate the magnitude and location of th e maximum deﬂection.

170 3 Energy Methods

3.22. A beam o f length 2L and ﬂexural rigidity EI is built-in at bo th ends z=±L and

subjected to a distributed lo ad w(z) per unit leng th, which is sy mmetric about the

mid-po int [i.e. w(−z)=w(z)]. Show tha t the trial function

u(z) =

∑

i=1



cos





−(−1)



satisﬁes the kinematic boundary conditions of the problem and use the Rayleigh-Ritz

method to ﬁnd the coefﬁcients C

in terms of integrals involving w(z). Evaluate the

resulting expressions for the special case where w(z)= w

3.23*. Figure P 3 .23 shows a beam of length L subjected to a uniformly distributed

load w

per unit length. The ends of the beam are simply supported, but equal and

opposite moments are applied at the ends whose ma gnitude is just sufﬁcient to ensure

that the de ﬂection of the beam is exactly zero at the mid-point.

Figure P3.23

Use the Rayleig h Ritz method (with a two degree of freedom approximation) to

estimate the slope of the beam at the supports.

Hint: Sketch the deformed shape of the beam before you make your choice of

approximating function and make sure that your choice is capable of describing the

shape of your sketch.

3.24. Use the Rayleigh-Ritz meth od with a on e degree of freedom app roximation to

estimate the displacement under the loa d for th e beam on three suppo rts shown in

Figure P3 .24.

w per unit length

Figure P3.21

Problems 171

3.25. Figure P3.25 shows a cantilever beam of ﬂexural rigidity EI and length L,

subjected to the distributed load

w(z) = w



−



Figure P3.25

Use the Rayleigh-Ritz method to estimate the deﬂection at the free end. Use a

polynomial approximating function with one degree of freedom, but which satisﬁes

the condition of zero bending moment at the free end.

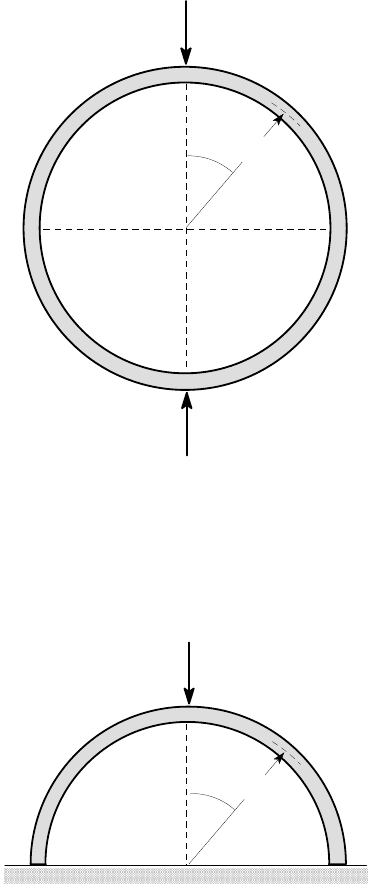
3.26. Figure P3.26 shows a simply-supported beam of length L and ﬂexural rigidity

EI, loaded by a moment M

at one end. Use the Rayleigh-Ritz method to approxi-

mate the deformed shape of the beam and hence estimate the maximum deﬂection.

Use a one degree of freedom polynomial. Greater accuracy will be obtained if

you choose a polynomial that gives zero bending moment at the unloaded end, in

addition to satisfying the kinematic boundary conditions (see §3.6.2).

Figure P3.24

Figure P3.26

w(z) per unit length

172 3 Energy Methods

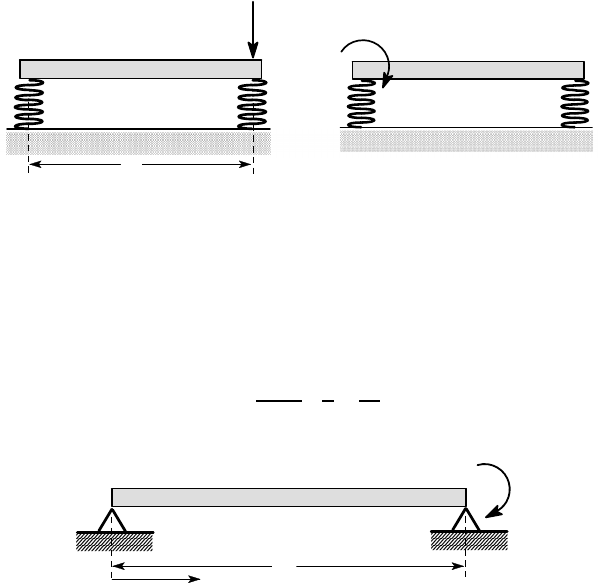
3.27. A complete circular ring of radius R and ﬂexural rigidity EI is subjected to

two equal and opposite forces F on a diameter, as shown in Figure P3.27. Use the

Rayleigh-Ritz method with a one degree of freedom approximation to the deformed

shape to estimate (i) the reduction in the diameter AC, (ii) the increase in diameter

BD and (iii) the bending moment in the beam at A.

Figure P3.27

3.28. A semicircular curved bar of radius R and ﬂexural rigidity EI is pressed against

a rigid frictionless plane by a concentrated force F at B, as shown in Figure P3.28.

Use the Rayleigh-Ritz method with a one degree of freedom approximation to the

deformed shape to estimate the change in the diameter AC due to the load.

Figure P3.28

Problems 173

Sections 3.7, 3.8, 3 .9

3.29. Use Castigliano’s ﬁrst theorem to solve Problem 3.15.

3.30. Use Castigliano’s ﬁrst theorem to solve Problem 3.18.

3.31. Use Castigliano’s ﬁrst theorem to solve Problem 3.19.

3.32. Find the displacements at A,B for the problem of Figure P3.32 (a), where AB is

a rigid bar and both springs have stiffness k. Use your results and Maxwell’s recipro-

cal theorem to determine the displacement at B due to the concentrated moment M

in Figure P3.32 (b).

Figure P3.32

3.33. The displacement u(z) for the simply supported beam of Figure P3.33 (a)

loaded by an end moment M

is given by

u(z) =

6EI



−



Figure P3.33 (a)

Use this result and Maxwell’s reciprocal theorem to ﬁnd where the force F should

be placed on the beam of Figure P3.33 (b) if the slope of the beam at B is to be a

maximum. What is the resulting maximum value?

(a) (b)

174 3 Energy Methods

Figure P3.33 (b)

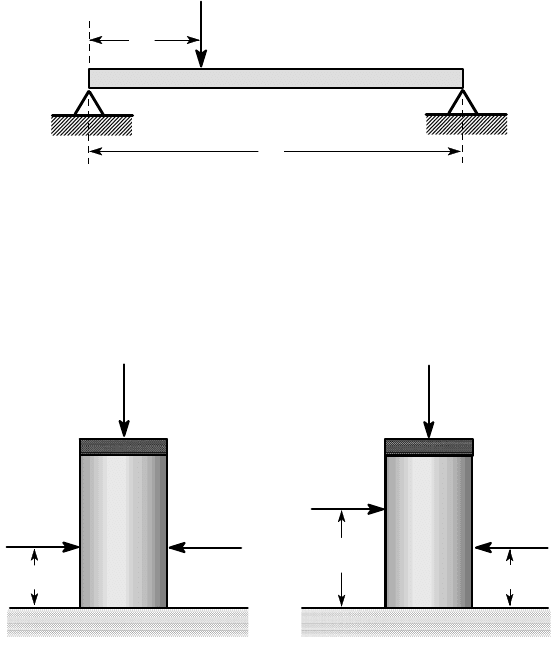
3.34. A cylinder of rubber of diameter D and length L rests on a ﬂat surface and is

loaded by a force F

applied through a ﬂat rigid plate. Both surfaces are frictionless

and the rubber has Young’s modulus E and Poisson’s ratio

=0.5.

Figure P3.34

The cylinder is now pinched by two colinear forces F

as shown in Figure

P3.34 (a). Use Maxwell’s reciprocal theorem with a suitable elementary state of

stress as auxiliary solution to ﬁnd the vertical displacement of the rigid plate due

to the forces F

3.35. The two forces F

in Problem 3.34 are now separated by a distance d vertically

as shown in Figure P3.34 (b). How much does the rigid plate rotate as a result?

3.36. Find the coefﬁcients of the 4 ×4 stiffness matrix K for the system of four

masses connected by springs shown in Figure P3.36.

(a + d)

(a) (b)