Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

3.8 Linear elastic systems 135

The maximum torque corresponds to the positive sign in this equation.

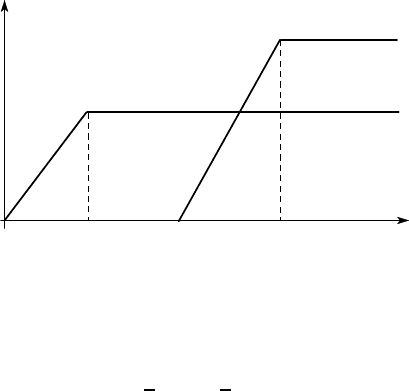
From a design point of view, the mechanism of Figure 3.21 is not very satisfac-

tory for a torque wrench, since the wrench would feel ‘springy’ — i.e. signiﬁcant

motion of the handle would have to occur before the preset maximum torque was

achieved and this might make the wrench unusable in some situations. A simple way

of avoiding this problem would be to introduce a stop permitting the spring to be

precompressed to a value slightly below that at snap-through, as shown in Figure

3.23.

Figure 3.23: Modiﬁcation to the torque wrench design to reduce spring motion before

snap through

If we continue to deﬁne

as the conﬁguration at which the spring would be

relaxed (although that position can now no longer be reached because of the stop),

the stop would have to be located such that the angle

with the slider touching the

stop is slightly larger than

as deﬁned by (3.73). This deﬁnes a suitable position

for the stop if the wrench is to be preset for a single value of torque. The wrench can

be made adjustable by allowing the position of the ﬁxed end of the spring D to be

changed, thus changing the rest position

. In this case, a mechanism would have to

be devised to make a simultaneous change in the position of the stop.

3.8 Linear elastic systems

For the remainder of this chapter, we shall restrict attention to systems in which the

displacements are small and linearly proportional to the applied loads, in which case

the principle of linear superposition applies. In other words, the displacement at any

point due to a system of loads is simply the sum of the displacements that would be

produced by each of the loads acting separately.

Suppose the elastic system is kinematically (not necessarily determinately) sup-

ported and subjected to a system of N external forces F

. As in §3.7, we shall denote

the displacement component in the direction of the force F

at its point of application

by u

The reader might like to investigate the signiﬁcance of the negative sign in equation (3.73),

by sketching the complete graph of T as a function of

in −

. It will be found

that there are two more stationary points — one maximum and one minimum — involving

conﬁgurations in which the spring is in tension.

C D

stop

136 3 Energy Methods

The principle of linear superposition then permits us to write

= C

+ ...C

i j

+ ...

∑

j=1

i j

, (3.74)

where C

i j

is the displacement component u

due to a unit force F

acting alone.

We shall call the coefﬁcients C

i j

inﬂuence coefﬁcients. They can also be regarded

as the elements of a matrix C, which is called the compliance matrix.

3.8.1 Strain energy

The total strain energy stored in the system can be found by equating it to the work

done during the application of the forces. However, if there is more than one external

force, we could envisage several scenarios for this loading process, since the order

of application of the forces is arbitrary. If the structure is elastic, the ﬁnal state (and

hence the total strain energy) must be independent of the loading history, and we

can therefore conclude that the total work done by the external forces must be the

same for all of these loading scenarios. This argument can be exploited to deduce

relationships that must exist between the inﬂuence coefﬁcients C

i j

To ﬁx ideas, suppose there are only two external forces F

. We consider three

scenarios:-

(i) F

applied ﬁrst, then F

time

Figure 3.24: Variation of the forces F

with time

This scenario is depicted in Figure 3.24. During the ﬁrst phase of the loading, F

and F

increases from zero to its maximum value. The work done is therefore

from equation (3.6).

3.8 Linear elastic systems 137

We now hold F

constant, whilst gradually applying F

. The additional work done

during this phase of the process is

∆

+ F

∆

where

∆

are the changes in u

respectively during (and due to) the ap-

plication of F

. Notice how F

does an additional amount of work ‘involuntarily’ as

it moves due to the action of F

. Notice also that there is no factor of 1/2 in the

term F

∆

, since the force F

is at its maximum value throughout the period during

which displacement

∆

occurs. You can check this by looking at Figure 3.24. By

contrast, F

is increasing linearly from zero with

∆

during this process.

Since the total work done during both phases of the loading process must be

stored as strain energy, we have

U = W

. (3.75)

(ii) F

applied ﬁrst, then F

Suppose we now consider a similar scenario, except that the load F

is applied ﬁrst,

followed by F

. The argument is unchanged, except that the sufﬁces 1,2 are reversed,

with the result

U =

(3.76)

for the ﬁnal strain energy.

(iii) F

applied simultaneously and in proportion

time

Figure 3.25: Simultaneous application of the forces F

Finally, we consider the scenario illustrated in Figure 3.25, in which both loads

increase slowly from zero together, such that the ratio F

is constant and equal to

its ﬁnal value. In the time interval

∆

138 3 Energy Methods

∆

= C

∆

;

∆

= C

∆

and the incremental work done (neglecting second order terms) is

∆

U = F

∆

+ F

∆

Integrating over the period of application of the forces, we ﬁnd the total work

done and hence the ﬁnal strain energy is

U = W =

. (3.77)

Each of the three scenarios considered lead to different expressions, (3.75, 3.76,

3.77) for the ﬁnal strain energy, but the ﬁnal state is independent of the order of ap-

plication of the loads and hence these expressions must all be equal. Examination of

the equations shows that this will be the case if and only if C

. More generally,

if there are N forces and displacement components, as in equation (3.74), we must

have

i j

= C

. (3.78)

In other words, the compliance matrix C must be symmetric. An incidental advan-

tage of this result is that it is not necessary to be too scrupulous about deﬁning the

order of the sufﬁces i, j in equations like (3.74). This is a statement of Maxwell’s

reciprocal theorem for linear elastic structures.

The expression for U when there are N forces is conveniently written in the form

analogous to (3.77) as

U =

∑

i=1

∑

j=1

i j

. (3.79)

This result can be established using a scenario similar to (iii) above, in which all the

forces F

are increased slowly and in proportion from zero to their ﬁnal values.

3.8.2 Bounds on the coefﬁcients

If we apply an external force or a system of external forces to an initially unloaded

linear elastic structure, the work done must be positive and the strain energy must

increase.

If this were not the case (i.e. if there were some system of loads that could

be applied that would allow energy to be recovered from the system), a theoretically

unbounded amount of energy could be recovered by applying a sufﬁciently large

load, violating the ﬁrst law of thermodynamics. It follows that U ≥0 for all possible

in equation (3.79).

This inequality imposes various constraints on the properties of the matrix C,

which can be explored by letting the F

take special values. The simplest example is

Since (3.74) is true for arbitrary F

, we can prove this more general result for any particular

i, j by replacing 1,2 in the above argument by i, j, respectively.

Strictly, the work done may also be zero, if motion in that direction is regidly restrained,

but it cannot be negative.

3.8 Linear elastic systems 139

that in which all the forces are zero except one, which can be of arbitrary magnitude

F. For example, writing F

=F, F

=0 (i6=k), we obtain

U =

≥0 ,

from (3.79), which implies that

≥ 0 . (3.80)

In other words, all the diagonal elements of C must be non-negative. In physical

terms, this means that when a force is applied to the structure, the displacement at

the point of application must have a non-negative component in the direction of the

force.

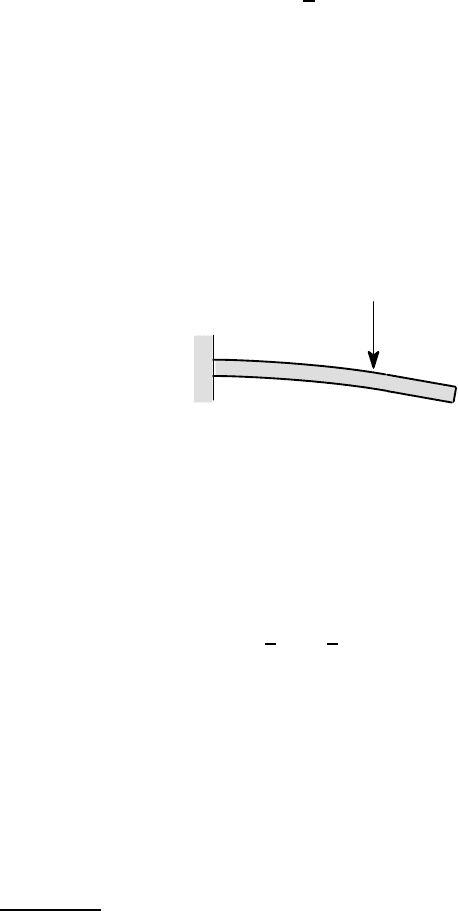
Intuitively, we might expect that a force will produce a greater displacement at

its point of application than at other points, which would imply that the diagonal

elements of C are generally greater than the off-diagonal elements. However, it is

easy to ﬁnd counter examples, such as the cantilever beam shown in Figure 3.26.

Figure 3.26: The beam subjected to a force F

If a force F is applied at the point A, the beam will deform as shown and, in particular,

the displacement at the end B will be greater than that at the point of application of

the load.

Nonetheless, inequalities can be established showing that the diagonal elements

tend on average to be greater than the off-diagonal elements. For example, writing

=1, F

=−1, F

=0 (i 6= j,k), we obtain

U =

j j

−C

≥ 0

and hence

j j

≥ 2C

. (3.81)

The alternative choice F

= 1, F

= 0 (i 6= j, k) — i.e. changing the sign of F

— leads to the related condition

j j

≥ −2C

, (3.82)

which would be a stronger constraint if C

<0. Notice that the off-diagonal elements

are not constrained to be non-negative. In fact, their signs depend on the convention

For those readers familiar with the summation convention in continuum mechanics and

tensor notation, we note that, in this and subsequent expressions, the notation C

etc does

not imply any summation over permissible values of k.

140 3 Energy Methods

adopted for the directions of the applied forces. Conditions (3.81, 3.82) can be sum-

marized as

j j

≥ |2C

| . (3.83)

Another inequality governing the relative magnitudes of diagonal and off-diagonal

elements can be obtained by choosing F

such that u

= 0, which is achieved if

=−C

, F

=0 (i6= j,k). We then obtain

U =

j j

−

and this expression is non-negative if and only if

j j

≥C

. (3.84)

3.8.3 Use of the reciprocal theorem

Maxwell’s reciprocal theorem tells us that if we apply a force F at point A and mea-

sure a component of displacement u at point B, the result we shall obtain is the same

as if the force had instead been applied at B in the direction of u and the displacement

had been measured at A in the direction of F. In other words, two different problems

for the same structure have the same solution. If we want to solve one of these prob-

lems, we therefore have a choice — we can solve the original problem or we can

solve the auxiliary problem related to it by the reciprocal theorem, since they both

have the same solution. The reciprocal theorem is useful in a particular case if and

only if the auxiliary problem is easier to solve than the original problem.

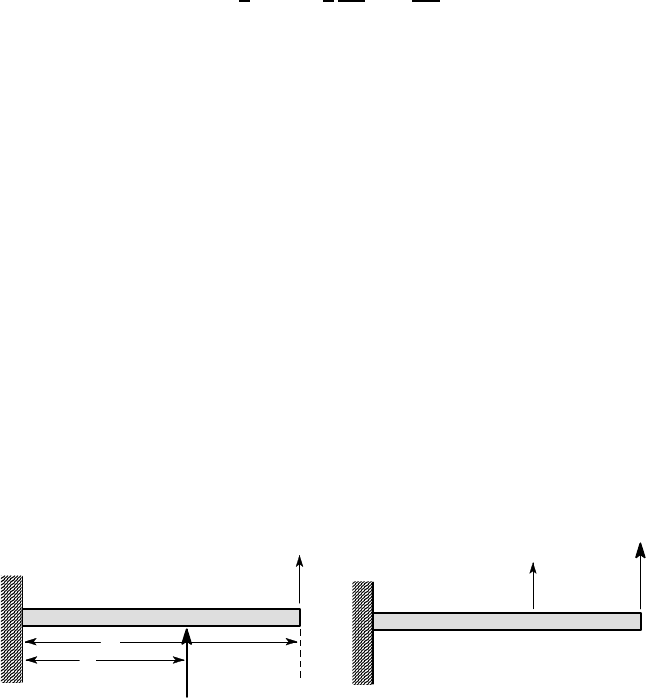
Example 3. 10

Determine the displacement u

at the end of the beam in Figure 3.27(a) due to the

force F applied at A.

(a) (b)

Figure 3.27: Cantilever (a) loaded by a force at an intermediate point and (b) the

auxiliary problem

The reciprocal theorem tells us that the required displacement u

is the same as

the displacement u

in the auxiliary problem of Figure 3.27(b), in which the load is

3.9 The stiffness matrix 141

applied at the end of the beam. This is arguably an easier problem than that of Figure

3.27(a), since using direct methods, we should need to use a singularity function

description of the bending moment. By contrast, the bending moment in the auxiliary

problem is

M = −F(L −z) = −EI

and hence, after integration and imposing the built-in end conditions at z = 0, we

obtain

u =

FLz

2EI

−

6EI

Maxwell’s theorem shows that this is also the solution for the end deﬂection u

the problem of Figure 3.27(a), provided we replace z by a — i.e.

FLa

2EI

−

6EI

. (3.85)

3.9 The stiffness matrix

The system of linear algebraic equations (3.74)

∑

j=1

i j

or u = CF (3.86)

can be solved to give F

in terms of u

in the form

∑

i=1

or F = Ku , (3.87)

where

K = C

−1

(3.88)

is the inverse of C. It follows that the matrix K is also symmetric and it is called the

stiffness matrix.

The coefﬁcient K

i j

is the force F

induced if u

= 1 and all other nodal displace-

ments are maintained at zero (i.e. u

=0 for all k6= j). These coefﬁcients are generally

easier to calculate that the inﬂuence coefﬁcients C

i j

, since the deformation is local-

ized near the node that is allowed to move. It also follows that many of the coefﬁ-

cients K

i j

will be zero. To understand this, consider the elastic truss shown in Figure

3.28, with nodes A,B,C, ..., nodal displacements u

,. .. and interconnecting

elastic bars.

To ﬁnd a given coefﬁcient K

i j

we ﬁx all the nodes except one, at which the dis-

placement component u

=1. For example, the coefﬁcients K

correspond to the case

where the node C moves vertically upwards. The only bars that will change in length

are CE,CF and hence the only nodes at which forces will be induced are E,F and of

course C. This means that the elements K

will all be zero,

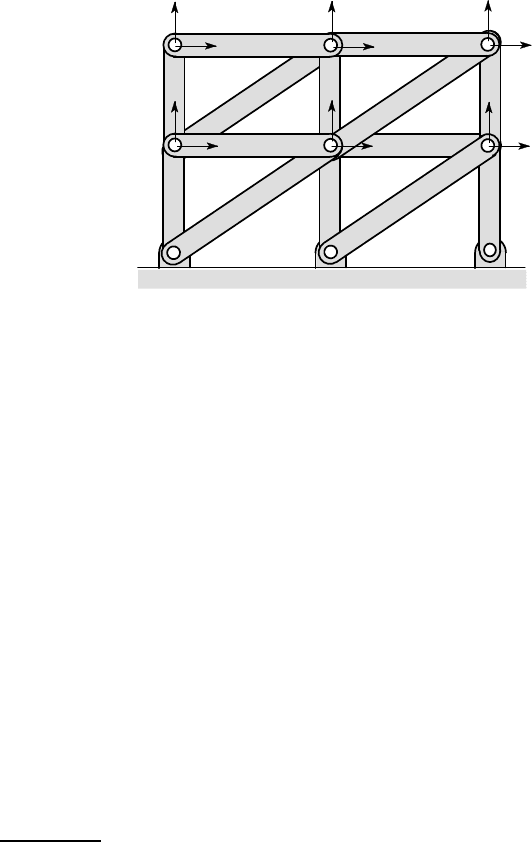
142 3 Energy Methods

since no forces are induced at A, B,D when u

is the only non-zero displacement.

More generally, in a structure like that of Figure 3.28, an off-diagonal element K

i j

will be non-zero only if u

are two orthogonal displacement components for the

same node or if there is a bar directly

connecting the nodes at which u

occur.

For this reason, with a suitable labelling scheme, K is generally a banded matrix —

i.e. the non-zero elements are clustered in a band near the diagonal.

Figure 3.28: A system of interconnected elastic bars

We can now see why it is generally easier to determine the stiffness matrix than

the compliance matrix. To determine K for the truss of Figure 3.28, we simply dis-

place each node in turn; determine the new lengths of the bars connecting that node

to the remaining ﬁxed nodes; determine the bar forces from Hooke’s law and hence

use equilibrium to determine the non-zero nodal forces. For each node, this involves

an analysis only of part of the structure — for example the section BCEF when we

are dealing with node C.

By contrast, if we wish to determine the compliance matrix directly, we have to

ﬁnd the displacements of all nodes due to the application of a force at each node in

turn. Every calculation involves an equilibrium analysis and a kinematic analysis of

the whole structure, which can be very lengthy if there are many nodes. It is therefore

generally much simpler to calculate K and then use (3.88) to determine C if it is

required.

3.9.1 Structures consisting of beams

Similar methods can be used to analyse systems of bars in bending and torsion. In

this case, deformation can only be localized in a part of the structure if each non-

active node is restrained against both translation and rotation. In the most general

three-dimensional case, we therefore identify 6 degrees of freedom (3 translations

In other words, not passing through some other node.

Similar matrices arise in the formulation of the ﬁnite element method and special schemes

have been developed for their efﬁcient manipulation (see Appendix A, §A.6).

3.9 The stiffness matrix 143

and 3 rotations) at each node and a corresponding set of 3 nodal forces and 3 nodal

moments. If just one displacement component (degree of freedom) is non-zero, the

deformation mode for each bar is then equivalent to that for a bar built in at one end

and either translated or rotated (but not both) at the other.

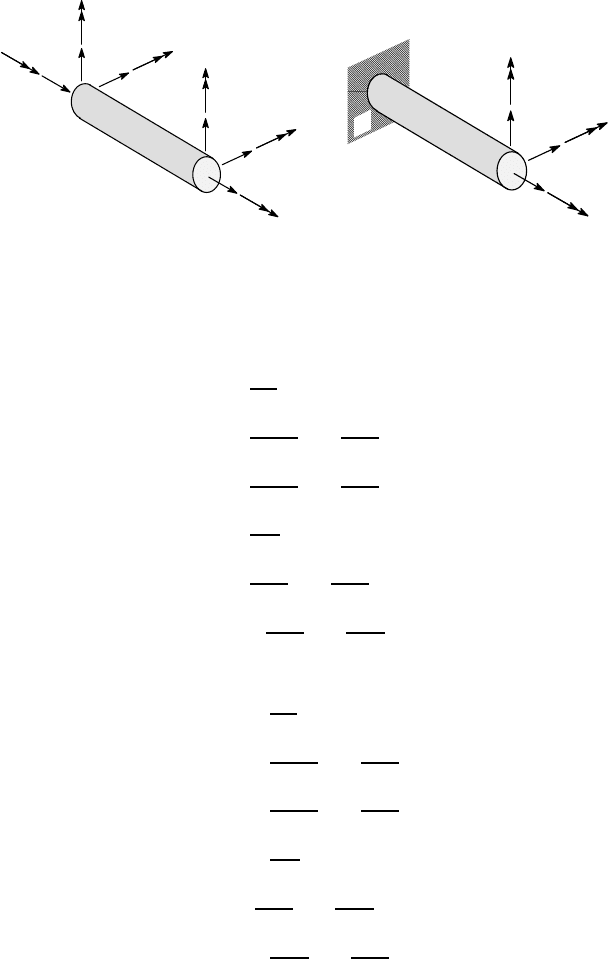
Figure 3.29: (a) Load and (b) displacement components for a built-in elastic bar

The load and displacement components for a typical bar are shown in Figure 3.29,

where A is the built-in end. The forces and moments at the free end B can be found

by elementary beam theory in terms of the degrees of freedom as

P =

12EI

−

6EI

12EI

6EI

T =

6EI

4EI

= −

6EI

4EI

. (3.89)

We also record the reaction forces and moments

= −

12EI

6EI

= −

12EI

−

6EI

= −

6EI

2EI

= −

6EI

2EI

. (3.90)

(a) (b)

144 3 Energy Methods

Example 3. 11

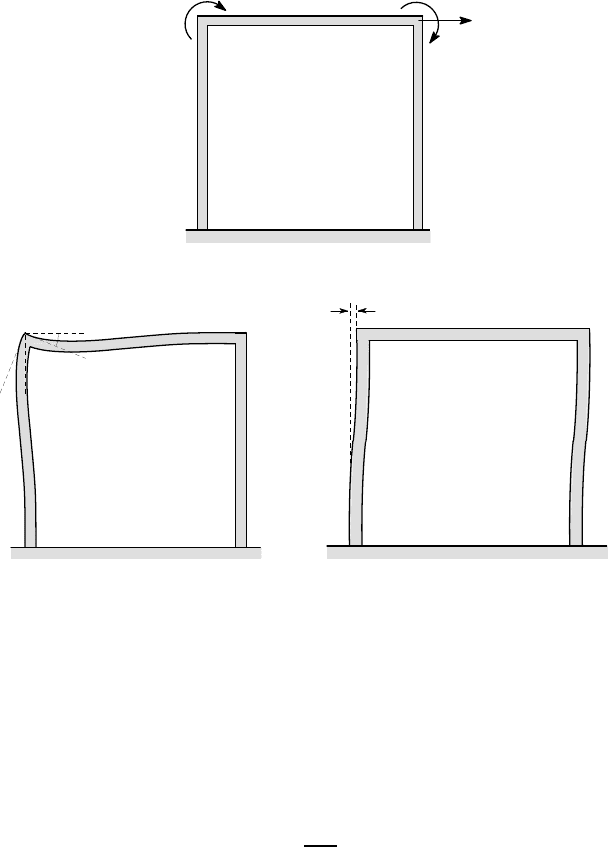
Find the coefﬁcients of the stiffness matrix for the two-dimensional rectangular frame

of Figure 3.30 (a), relating the force F and moments M

to the corresponding

displacement u and rotations

. Assume that the beam segments are much stiffer

in tension than in bending and that each has length L and ﬂexural rigidity EI.

M , θ

F, u

(a)

(b) (c)

Figure 3.30: A rectangular frame with three degrees of freedom: (a) Force and dis-

placement components, (b) rotation of node B, (c) translation of bar BC

Since the beam segments are much stiffer in tension than in bending, the only

degrees of freedom comprise rotation of the joint B, rotation of the joint C and hor-

izontal translation of the member BC without rotation. Figure 3.30 (b) shows the

conﬁguration with

= 0 and u =0. The beams AB and BC are both rotated through

a clockwise angle

at the end. To hold AB in this conﬁguration, we require a hori-

zontal force

F = −

6EI

and a clockwise moment