Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

3.3 Load-displacement relations 105

+ F

cos30

= 0 (3.16)

sin30

+ F = 0 (3.17)

and hence

√

3F ; F

= −2F . (3.18)

As we might expect, spring 2 is in compression (F

<0) and spring 1 is in tension.

The energy stored in each spring U

is given by equation (3.7) with appropri-

ate values of F,k, and hence the total strain energy is

U = U



√



(−2F)





. (3.19)

Now the total strain energy U must also be equal to the work done by the force

F during its application. The structure as a whole is linear elastic and obeys Hooke’s

law, so the work done by F is

W =

Fu , (3.20)

by analogy with equation (3.6), where u is the displacement component at A in the

direction of F — i.e. the vertical component of the displacement at A.

Equating U and W, we obtain

Fu =





and hence

u =





F , (3.21)

which deﬁnes the vertical displacement of the point A due to the force F.

Equation (3.21) can be regarded as deﬁning a stiffness k for the structure as a

whole, such that





. (3.22)

In this context, it is worth noting that any linear elastic structure can be thought of

as an equivalent single spring insofar as an applied force produces a proportional

displacement at its point of application.

The procedure illustrated in this example is considerably easier than a direct

solution, which would involve:-

It is a good idea to adopt the convention that the forces in all axial members and springs

are denoted by positive symbols when they are tensile, even when our intuition enables us

to judge immediately that one or more of the forces in the system will be compressive.

106 3 Energy Methods

(i) Finding the forces in the springs as in equations (3.16–3.18) above,

(ii) Using Hooke’s law to determine the deformed lengths of the two springs,

(iii) Using kinematic (geometric) arguments to deduce how the deformed springs

will ﬁt together and hence determine the displacement of the point A.

The ﬁrst two stages of the direct solution would be quite straightforward, but the

kinematic argument (iii) can be quite complicated, particularly for a more complex

interconnected structure such as that of Problem 3.12. The energy method used here

replaces the kinematic argument to which it is therefore mathematically equivalent,

though this fact is far from intuitively obvious.

The energy method developed in this section only works if there is a single (ex-

ternal) force F, since if there were more than one force, we would not be able to

separate their individual contributions to the work done on the system. Furthermore,

the method only gives the displacement in the direction of the force and at its point

of application. In Example 3.2, the point A will also have a horizontal component of

displacement, which does not feature in the work done because it is orthogonal to the

applied force, and which therefore cannot be found by the present method. However,

later in this chapter, we shall develop ways of overcoming these limitations.

3.3.1 Beams with continuously var ying bending moments

Equations (3.10–3.12) deﬁne the strain energy in a beam subjected to uniform bend-

ing, but in most beam problems the bending moment M(z) varies with distance z

along the length. We can extend the argument to this case by regarding the beam as

made up of a set of beam segments of inﬁnitesimal length

The strain energy in the segment between z and z+

z is

U =

2EI

, (3.23)

from equation (3.12) and hence the total strain energy in the beam 0< z <L is

U =

, (3.24)

where we have left the ﬂexural rigidity EI under the integral sign, since this also may

vary with z in some cases. For example, the cross section of the beam (and hence the

second moment of area I) may vary along the length.

Example 3. 3

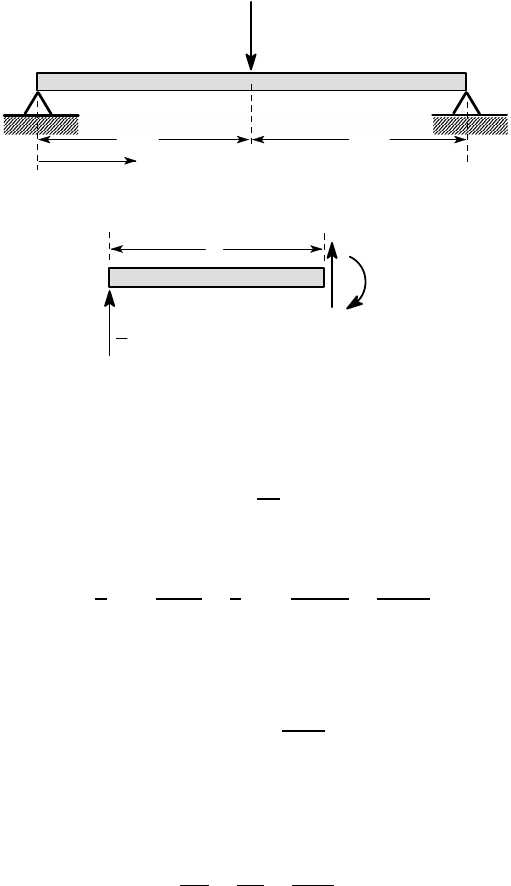
Find the central deﬂection of the simply-supported beam of Figure 3.6 (a) due to a

central force F.

By symmetry, the two end reactions are each F/2 and the bending moment at a

distance z from the left support in the segment 0 < z < L/2 can be found from the

free-body diagram of Figure 3.6 (b) as

3.3 Load-displacement relations 107

(a)

(b)

Figure 3.6: A simply-supported beam with a central force

M = −

. (3.25)

The strain energy stored in the beam segment 0< z <L/2 is therefore

L/2

4EI

192EI

from equation (3.25). By symmetry, there must be an equal amount U

of energy

stored in the other half of the beam L/2<z< L and hence the total strain energy,

U = U

96EI

As in Example 3.2, we can deduce that the work done in (slowly) applying the force

is W =Fu/2, where u is the downward deﬂection under the load. The work done W

and the energy stored U must be equal and hence the central deﬂection of the beam

due to the force F is

u =

48EI

. (3.26)

3.3.2 Axial loading and torsion

Essentially similar results can readily be obtained for bars loaded by axial forces and

torques. We ﬁrst note that a bar of cross-sectional area A and length L, subjected to a

L /2L /2

108 3 Energy Methods

uniform axial tensile force F will experience a uniform tensile stress

=F/A and a

strain

=F/EA. The extension will therefore be

u =

. (3.27)

The relation between F and u is similar to that illustrated in Figure 3.3 and it follows

that the work done on loading and the stored strain energy are

U = W =

Fu =

2EA

EAu

, (3.28)

where the alternative expressions are obtained by substituting for u or F respectively

from (3.27).

If the axial force F or the product EA varies along the bar, we consider the bar as

a set of segments of length

z as in §3.3.1 obtaining the integral expression

U =

. (3.29)

Similarly, if a uniform circular bar

of length L is loaded by a uniform torque T,

the strain energy is

U =

2GJ

(3.30)

and if either the torque or the polar moment of area varies along the bar

U =

. (3.31)

3.3.3 Combined loading

If a beam is subjected to simultaneous bending, torsion and axial load, the energy

stored is the sum of that associated with the three loads separately. This is not a

trivial result, since the energy expressions are quadratic (not linear) in the loads and

the principle of superposition does not generally apply. However, it does apply in

the present case because the deformations of each mode of loading are orthogonal

to the other loads. For example, torsion does not cause any extension of the bar, so

Important Note about the torsion equation. The elementary torsion formula (1.18) only

applies for circular sections. However, the relation between torque and twist can be gen-

eralized to non-circular sections if the polar moment of area J is replaced by a different

quantity K which reduces to J in the case of the circle. For sections that deviate signiﬁ-

cantly from the circle (in particular for thin-walled open sections), K can be several orders

of magnitude smaller than J so it can be catastrophic to use the elementary torsion for-

mula out of context. The problem of ﬁnding K for thin-walled sections will be addressed

in Chapter 6 below. Results have been obtained either by analytical or numerical methods

for a wide range of important sections and a table of such values is given by R.J. Roark and

W.C. Young (1975), Formulas for Stress and Strain, McGraw-Hill, Table 20.

3.3 Load-displacement relations 109

if a torque is applied to a bar in tension, the resulting deformation does not cause

the axial force to do additional work. In order to preserve orthogonality between

axial forces and bending moments, it is essential that the axial force be deﬁned to

act through the centroid of the beam cross section. An eccentric force must therefore

be decomposed into an equal force acting through the centroid and an appropriate

bending moment.

Beams are much stiffer in extension than they are in bending or torsion. For ex-

ample, an ordinary wooden or plastic ruler can be visibly twisted and bent about its

weaker axis by hand, whereas no visible extension can be produced. Since the en-

ergy stored is equal to the work done, which in turn is the product of the force and

the distance through which it moves, it follows that more energy is generally stored

in modes that involve signiﬁcant deformations. Thus, if a beam is loaded simultane-

ously by a bending moment, a torque and an axial force, the strain energy associated

with the axial force can generally be neglected.

3.3.4 More general expressions for strain energy

If the stress ﬁeld in a body varies in a more general way, the strain energy can be

computed by considering the body as made up of a set of inﬁnitesimal elements of

material of volume

V over which the stresses can be considered uniform, and then

summing the resulting expressions over the total volume of the body V by integra-

tion.

We showed in §2.2.3 that the strain energy stored per unit volume is

−2

(

)

+ 2(1 +

)(

)

from equation (2.32). The total strain energy can therefore be written in the integral

form

U =

ZZZ

dV (3.32)

ZZZ

−2

(

)

+ 2(1 +

)(

)

dV . (3.33)

3.3.5 Strain energy associated with shear forces in beams

If equation (3.33) is applied to a beam transmitting both bending moments and shear

forces, it is clear that the shear stresses associated with the shear force will make a

contribution to the total energy. However, for slender beams it is always small com-

pared with the energy associated with the bending stresses. Inclusion of the energy

due to shear is equivalent to other methods of taking account of additional deﬂections

110 3 Energy Methods

due to shear. It typically leads to an increase in the predicted displacements of 5% or

less

and there are very few engineering applications where this level of accuracy is

required.

3.4 Potential energy

Most readers will have encountered the concept of potential energy in physics or

mechanics courses concerned with the motion of masses in a gravitational ﬁeld. If we

lift a body of mass M through a height h, we have to do work against the gravitational

force Mg. The work done is equal to the product of the force and the distance through

which it acts — i.e.

W = Mgh . (3.34)

Notice that there is no factor of 1/2 in this equation, in contrast to equation (3.6).

This is because in lifting the mass, the full gravitational force Mg has to be opposed

throughout the motion, whereas in extending the spring, the force increases gradually

during the extension from zero to its maximum value, as shown in Figure 3.3.

The work done in lifting the mass can be recovered by lowering it again in a con-

trolled manner, so that the gravitational force does work on the system. We therefore

describe the mass as having potential energy in its raised state, equal

to the work

done in lifting it Mgh.

Suppose a ball of mass M is constrained to move in a frictionless groove, as

shown in Figure 3.7. Intuitively, it is clear that the only positions where the ball

may remain at rest are the points A,B,C, where the groove is locally horizontal.

Furthermore, if the ball were slightly displaced from A and then released, it would

tend to roll back to A, whereas if it were displaced from B it would tend to roll away

It might be argued that we could ﬁnd a counter example to this assertion by choosing a

loading that involves a large shear force and a small bending moment. However, the two

quantities are related through the equilibrium condition V = dM/dz, where V is the shear

force. A large shear force will therefore always be associated with a large bending moment,

unless the beam is very short, in which case the theory of slender beams is arguably not

applicable.

Strictly speaking, only the change in potential energy can be deﬁned this way, since there

is some ambiguity about the datum — i.e. the location at which the potential energy is

taken to be zero. For example, if the mass is resting on the ground, the gravitational force

could be caused to do additional work by transporting the mass horizontally to a mine shaft

and dropping it down. In Newtonian gravitational theory, all the mass in the universe was

assumed to be located in a bounded region surrounded by an inﬁnite empty space. Potential

energy could then be deﬁned unambiguously as the work that would have to be done to

transport a mass from the ‘point at inﬁnity’ (where there would be no gravitational force in

view of the inverse-square law) to its actual location. However, we do not need to appeal to

such abstruse notions, since we shall only be concerned with changes in potential energy

and the choice of datum is therefore arbitrary. This will be apparent in problems in that any

constants in the energy expressions will either be eliminated as a result of differentiation or

will cancel in the ﬁnal equations.

3.4 Potential energy 111

towards either A or C. We therefore describe A,C as stable equilibrium positions,

whilst B is an unstable equilibrium position.

Figure 3.7: The ball in a frictionless groove

We can establish these claims by energy arguments. We ﬁrst note that the ball

has to remain within the groove, which we express in technical terms by saying that

only positions within the groove are kinematically permissible. In the absence of

this constraint, the ball would have two degrees of translational freedom,

which can

be expressed by stating that we would need to know the horizontal and vertical co-

ordinates x,y of its centre in order to deﬁne its position. However, as long as the ball

is in the groove, knowledge of the x coordinate alone is sufﬁcient to deﬁne its posi-

tion, since there is only one position in the groove corresponding to any given value

of x. Thus, the kinematically constrained ball has only one degree of translational

freedom.

The potential energy

of the ball depends on its position in the groove and

hence on x. In fact we can write

(x) = Mgh(x) , (3.35)

where y = h(x) is the equation deﬁning the centreline of the groove in Figure 3.7.

Thus, the equilibrium positions A,B,C are all points where h

′

(x)= 0 and hence

∂Π

∂

= 0 . (3.36)

Furthermore, the stable positions A,C correspond to local minima in the potential

energy — i.e. points where

∂Π

∂

= 0 and

∂

> 0 . (3.37)

Now if the ball is instantaneously at rest at either A or C, it can only move by

passing initially through positions of higher potential energy. This in turn would

We shall not consider rotations here, since rotation of the ball about its axis does not affect

potential energy and, in a frictionless groove, no forces can be exerted on the ball tending

to rotate it.

h(x)

112 3 Energy Methods

require that work would have to be done on the ball to increase its potential energy.

In the absence of external forces other than gravity to do this work, the ball cannot

move and we conclude that a minimum potential energy position must also be a

position of equilibrium.

Suppose we now apply an external force to displace the ball slightly from A to

the point D in Figure 3.8 and then release it.

Figure 3.8: If the ball is released at D, the subsequent motion will be oscillatory

between the extremes D,E which have the same height h

The potential energy at D will exceed that at A, but again we can argue that the

ball cannot pass through any points of higher energy than it posessed at the moment

of release and hence it must remain in the region DAE. What will happen, of course,

is that the ball will accelerate back towards A, at which point the surplus of potential

energy will have been converted to kinetic energy. The ball will therefore oscillate

about the equilibrium position, interchanging potential and kinetic energy, but the

extremes of the motion will be circumscribed by the potential energy at the point of

initial displacement — i.e. they will be deﬁned by the point D and the point E on the

other side of A that has the same value of h as has D.

By contrast, if we displace the ball slightly from the equilibrium point B in Figure

3.7 where potential energy is a maximum, further motion away from B will lower the

potential energy. Since energy is conserved in the system (there is no friction), the

lost potential energy is converted to kinetic energy and the ball accelerates away from

B, which is therefore a position of unstable equilibrium.

All of these results could have been obtained using Newton’s second law, without

reference to potential energy. Since there is no friction, the reaction force at the

groove must be normal to the surface and hence pass through the centre of the ball

as shown in Figure 3.9.

Figure 3.9: Forces acting on the ball

Since there are only two forces acting — the reaction force and the gravitational force

— they can only be in equilibrium if they are equal and opposite, which will occur if

3.5 The principle of stationary potential energy 113

and only if the groove is horizontal. Furthermore, if the ball is instantaneously at rest

at a point where the groove is not horizontal, the acceleration will be in the direction

of the resultant force, leading to the conclusion that the ball will accelerate along

the groove in the direction of lower h. Thus, if the ball is displaced slightly from A

and released, it will tend to move back towards A, conﬁrming that A is a position of

stable equilibrium, whereas a similar displacement from B leads to forces tending to

accelerate the ball further away from B, indicating instability as before.

3.5 The principle of stationary potential energy

The results established above are true for more general systems and can be expressed

in the following statement:-

Out of all kinematically permissible conﬁgurations of an elastic system, those

at which the total potential energy is stationary with respect to any permis-

sible motion are equilibrium conﬁgurations. Those that represent local min-

ima of the total potential energy are stable equilibrium conﬁgurations, whilst

those representing local maxima of the total potential energy are unstable

equilibrium conﬁgurations.

Total potential energy

is to be interpreted here as the total recoverable mechan-

ical energy in the system and includes both energy stored as strain energy in elastic

members and the potential energy of the external forces. In the following derivations,

we shall generally use the symbol U for strain energy and

Ω

for the potential energy

of external forces such as gravity. Thus, the total potential energy can be written

= U +

Ω

. (3.38)

The intuitive reasoning behind the principle of stationary potential energy is the

same as that used in discussing the ball sliding in the frictionless groove of Figure 3.7.

If all kinematically possible small perturbations of the system from an equilibrium

position result in an increase in total potential energy, such motion is precluded by

the principle of conservation of energy. Furthermore, if the total potential energy is

a differentiable function of the degree(s) of freedom and if any derivative at a given

point is non-zero, it follows that there will be some direction of possible motion

in which total potential energy can decrease and hence the system can (and will)

accelerate.

Example 3. 4

Figure 3.10 (a) shows a rigid uniform beam ABC of length L and mass M, pinned at

A and supported by springs, each of stiffness k, at B,C. Find the downward vertical

displacement, u

of the end C. The forces in both the springs are zero when the bar

is in the horizontal position.

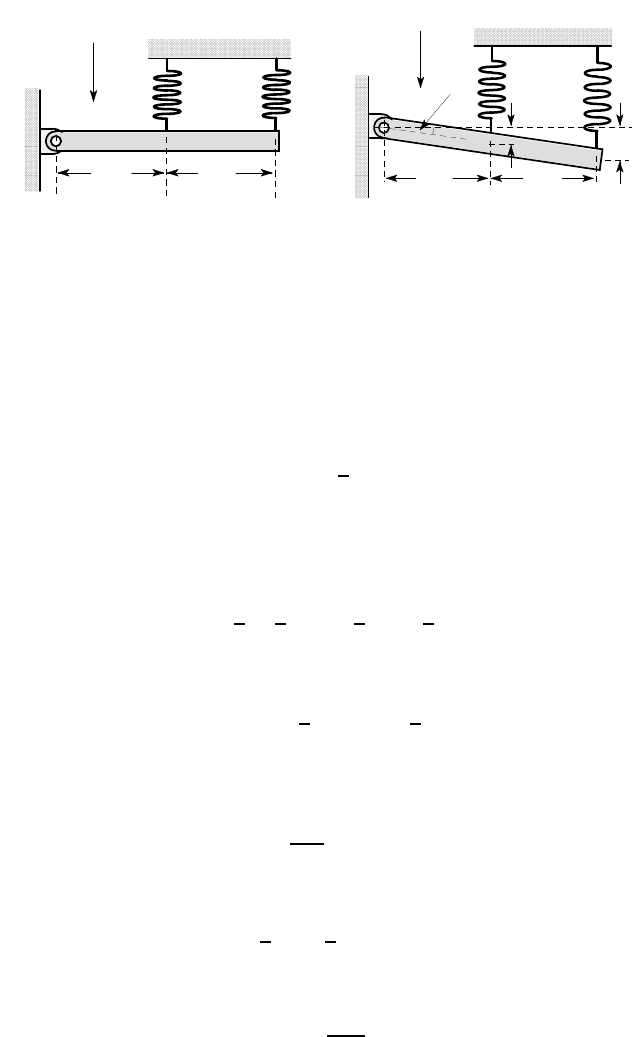
(a) (b)

Figure 3.10: A rigid beam supported by two springs

Since the beam is rigid, the only permissible conﬁguration consists of rotation

about the end A as shown in Figure 3.10 (b), in which case, the extension of spring B

will be u

/2.

In the deformed conﬁguration, there will be gravitational potential energy and

elastic strain energy in the springs. Suppose that the gravitational potential energy

Ω

is given by

Ω

when the bar is horizontal. In the deformed conﬁguration, we will

then have

Ω

−

Mgu

since the centre of mass of the bar falls during the deformation through a distance

/2.

The strain energy in the springs is the sum of that stored in each of the two springs

— i.e.

U =





and hence the total potential energy (strain energy + gravitational potential energy)

= U +

Ω

−

Mgu

. (3.39)

The principle of stationary potential energy now states that the equilibrium posi-

tion of the bar is that at which

is stationary with respect to permissible deforma-

tions — i.e.

∂Π

∂

= 0 .

Substituting for

from equation (3.39) and performing the differentiation, we

ﬁnd that

−

Mg = 0

and hence the vertical displacement of the end C is

2Mg

. (3.40)

L / 2

L / 2L / 2

(a) (b)

114 3 Energy Methods